剪力连接度对钢-混凝土组合梁桥力学性能的影响
2022-11-11赵兴宝邓文琴周海川张建东
赵兴宝,邓文琴,周海川,刘 朵,张建东
(1.南京工业大学土木工程学院,南京 211816;2.苏交科集团股份有限公司,南京 211112;3.江苏省交通运输厅公路事业发展中心,南京 210018)
钢-混凝土组合梁因其优越的力学性能和良好的经济性在桥梁工程领域中得到广泛应用,且相关技术快速发展[1-2]。钢-混凝土组合梁力学性能优越的原因在于混凝土桥面板与钢梁通过剪力连接件形成组合截面、协同受力,可充分发挥各自的材料特性[3-5]。反映钢-混凝土组合梁连接水平的剪力连接度是设计的关键点,《钢-混凝土组合桥梁设计规范》(GB 50917—2013)[6]中要求剪力连接件按完全抗剪设计,每个剪跨段内连接件的抗剪承载力总和须大于钢梁与混凝土桥面板接触面的纵向剪力,即剪力连接度大于1.0。
圆柱头栓钉因其稳定的力学性能和施工便捷性被广泛应用于钢-混凝土组合梁的剪力连接件构造中[7-9]。为确保桥梁结构的安全性,设计时通常以某一安全系数为参考,放大结构的剪力连接度,即通过提高栓钉数量或单个栓钉的承载力增大钢-混凝土组合梁的剪力连接度,从而形成一定的安全富余度。然而栓钉数量过多会造成材料浪费且会增加工程量,须合理把控用量。目前多通过缩尺模型试验、有限元数值模拟以及二者结合的方式研究剪力连接度的影响,因缩尺效应的限制,在现有研究中剪力连接度多小于1.5[10-14],且对实际工程中的剪力连接度研究较少。
本研究通过有限元数值模拟,建立起一座截面形式为槽形钢-混凝土组合箱梁的40 m跨简支梁桥的足尺有限元模型,并通过改变剪力连接度建立多组对比模型。对剪力连接度进行参数分析,研究其对钢-混凝土组合梁的抗弯承载力、相对滑移和破坏模式的影响,确定剪力连接度的合理取值范围。
1 工程概况
依托工程为40 m简支梁桥建设工程,截面形式为槽形钢-混凝土组合箱梁,结构截面如图1所示。槽形钢梁采用Q345qD材料,上下翼缘板厚度分别为25 mm和32 mm,腹板厚度为12 mm,横向加劲肋厚度均为10 mm,其中腹板横向加劲肋高度为140 mm,底板横向加劲肋高度为160 mm。组合梁顶板采用C50混凝土,箍筋采用HPB300级钢筋、直径为16 mm;纵向钢筋采用HRB400级钢筋、直径为20 mm。剪力连接件采用D22×200 mm圆柱头栓钉,材质为ML 15,槽形钢翼缘板上共布置1 584个栓钉。

图1 结构截面(单位:mm)
剪力连接度是反映钢-混凝土组合梁桥剪力连接水平的指标,剪力连接度r的计算公式为
r=n/nf
(1)
式中,n为剪跨段内实际布置的剪力连接件数目;nf为保证桥面板或钢梁进入全截面塑性的剪力连接件数目。
根据《钢-混凝土组合桥梁设计规范》(GB 50917—2013)[6]中的计算方法,可得组合梁完全抗剪设计所需栓钉数量nf为1 536个;实际工程中的剪力连接度r为2.0。
2 有限元模型
2.1 模型建立
为分析钢-混凝土组合梁在跨中集中荷载作用下的受力,建立有限元模型时考虑了材料非线性、几何非线性和接触非线性等特性。采用三维实体单元C3D8R模拟钢梁、栓钉及混凝土桥面板,采用桁架单元T3D2模拟普通钢筋。有限元模型示意如图2所示,根据结构的对称性建立1/4实桥模型。
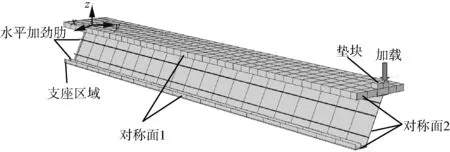
图2 有限元模型示意
2.1.1 材料本构
C50混凝土的轴心抗压强度标准值为32.4 MPa,轴心抗拉强度为2.65 MPa,弹性模量为3.45×104MPa,泊松比为0.167。混凝土材料采用《混凝土结构设计规范》(GB 50010—2010)[15]中的本构模型。对于钢材本构关系,由于其达到屈服后塑性流动较长,达到抗拉强度时变形较大,因此将钢材定义为理想弹塑性材料,采用双折线本构模型。钢材的弹性模量均为210 GPa,栓钉屈服强度为360 MPa,钢梁及钢筋强度按规范取值。
2.1.2 界面接触、边界条件及荷载施加
栓钉底面与钢梁上翼缘板绑定,栓钉整体内嵌于混凝土桥面板内。混凝土桥面板与钢梁上翼缘采用面-面接触,法向采用硬接触,切向采用罚函数法,摩擦系数为0.3。
将在支座位置长度为梁底宽、宽度为100 mm的区域设置为刚体,设置参考点与此刚体区域耦合,将边界条件施加在参考点上。在模型的两个对称面上建立对称边界条件,采用位移加载方法,跨中对称施加荷载。
2.2 模型验证
为验证该有限元建模方法的准确性,按上述建模方法与文献[11]中的同类型缩尺试验梁SPB1进行对比验证,有限元与试验荷载-跨中挠度曲线对比如图3所示,结果表明两者在弹性阶段吻合较好,试验梁屈服荷载为270 kN,有限元模型屈服荷载为301 kN,相差11%;塑性阶段有限元曲线略低于试验曲线,试验梁极限荷载为432 kN,有限元模型极限荷载为390 kN,略低于试验值,相差10%。所研究的有限元建模方法可以较好地模拟该类型桥梁的受力。研究中均为依托工程的足尺三维实体有限元模型,单元数量多、计算量大,为提高计算效率,将钢材视作理想弹塑性材料,未考虑相应材料的强化阶段。
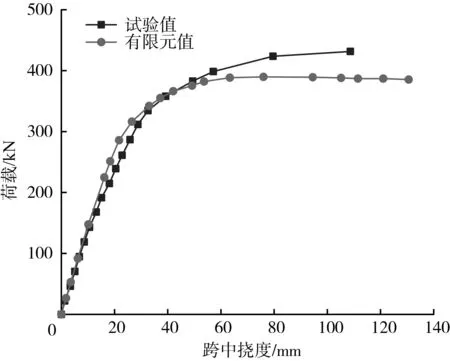
图3 有限元与试验荷载-跨中挠度曲线对比
3 剪力连接度的影响
以实际工程为基准模型(模型编号为R8),改变模型的栓钉数量,建立8组不同剪力连接度的有限元模型。调整栓钉间距使其布置合理,其余参数均不变。有限元模型栓钉连接件参数如表1所示,本文中r为剪力连接度。
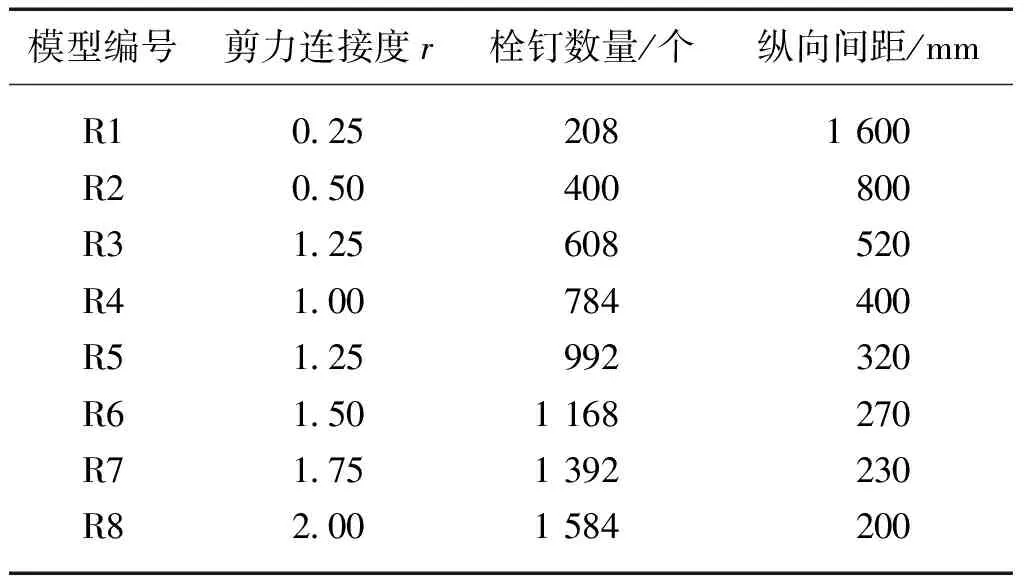
表1 有限元模型栓钉连接件参数
3.1 抗弯承载力
8组模型的荷载-跨中挠度曲线如图4所示,曲线分为弹性、弹塑性和塑性3个阶段:弹性阶段为近似上升直线,8组模型的曲线差异较小,可以看出剪力连接度对组合梁的初始抗弯刚度影响较小;随着荷载的增大,曲线进入弹塑性阶段,栓钉开始屈服导致组合梁截面相对滑移增大,当0.25≤r<0.75时组合梁弹塑性阶段抗弯刚度下降较为明显,下降幅度不断减小,当r≥0.75时组合梁弹塑性阶段抗弯刚度基本不变;截面中和轴上移,跨中钢梁底板开始屈服并向顶板扩展进入塑性阶段后,栓钉全部屈服,跨中钢梁全截面屈服,荷载-跨中挠度曲线斜率下降直至水平,8组模型极限荷载随着剪力连接度的增大而增大,增幅不断减小。将跨中钢梁底板屈服时的荷载视作组合梁的抗弯承载力,剪力连接度对抗弯承载力的影响曲线如图5所示,由图5可知,当0.25≤r<0.75时,组合梁的抗弯承载力不断增加;当r≥0.75时,组合梁的抗弯承载力增幅不断降低直至为0。因此从结构受力角度综合考虑组合梁抗弯刚度及抗弯承载力,取值时r≥0.75即可。

图4 8组模型的荷载-跨中挠度曲线
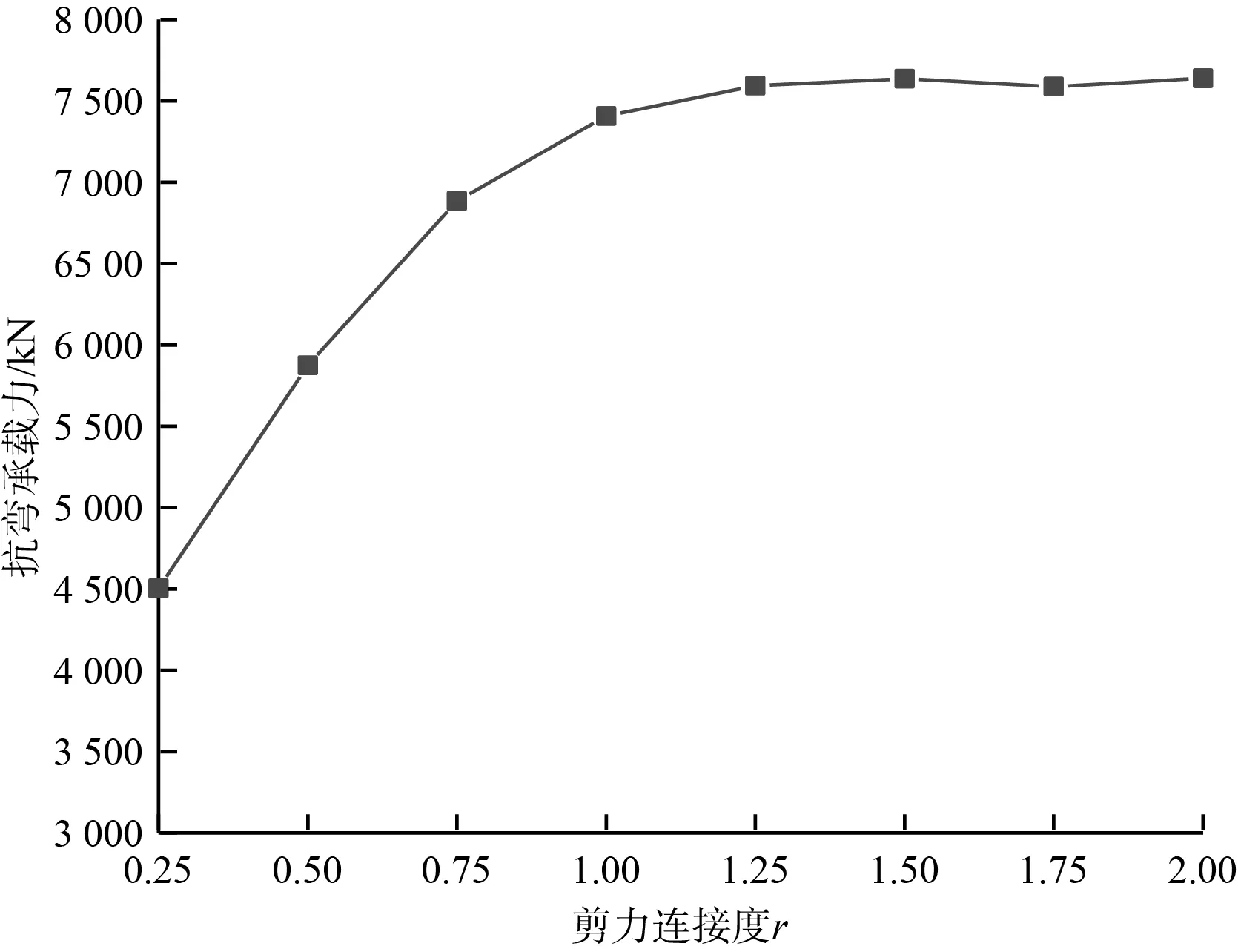
图5 剪力连接度对抗弯承载力的影响曲线
3.2 相对滑移
钢-混凝土组合梁桥面板与钢梁之间的相对滑移是体现组合梁整体受力性的重要参数。4 000 kN荷载下4组模型相对滑移沿纵桥向分布曲线如图6所示,在相同荷载下,当0.25≤r<0.75时,钢-混凝土组合梁的相对滑移与剪力连接度呈反比关系,即剪力连接度越大,组合梁相对滑移越小;当r≥0.75时,组合梁L/5跨截面的相对滑移近似为0(因r≥1.00的模型相对滑移均接近为0,故选取此4组为代表模型)。相对滑移沿纵桥向的分布规律为:从支座向跨中先增大后减小,最大滑移发生在L/10~L/5之间,跨中滑移均为0。

图6 4 000 kN荷载下4组模型相对滑移沿纵桥向分布曲线
7组模型组合梁L/5截面相对滑移-荷载曲线如图7所示,不同剪力连接度的组合梁的相对滑移-荷载曲线的变化趋势相同,大致可分为3个阶段:①加载初期,组合梁的相对滑移均为0;②随着荷载的增大,混凝土桥面板与钢梁之间由静摩擦变为滑动摩擦,相对滑移发生并随之增大;③组合梁进入塑性阶段后,荷载不再增大,而相对滑移继续增加。
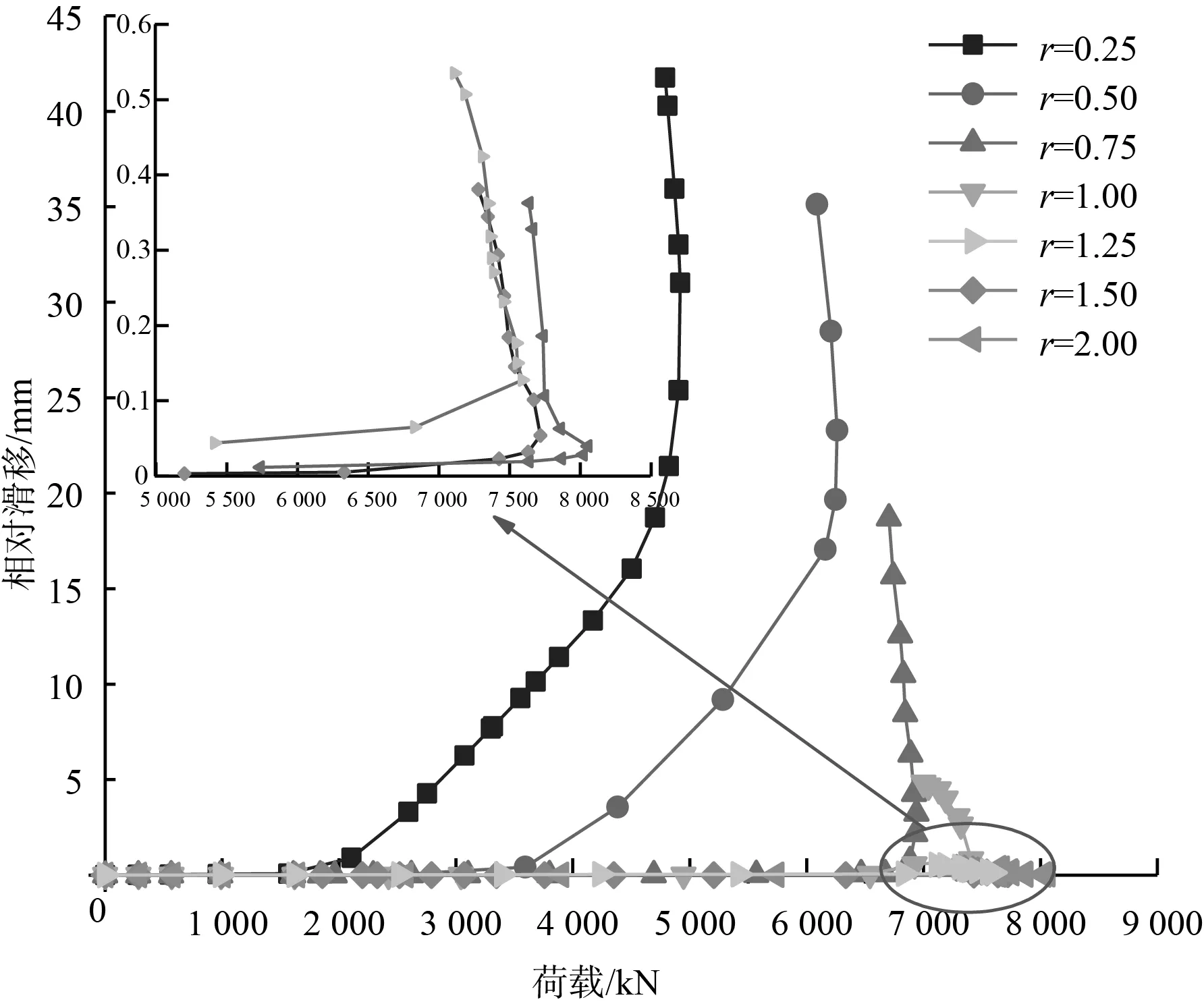
图7 7组模型组合梁L/5截面相对滑移-荷载曲线
由图7可知,随着剪力连接度的增大,组合梁的相对滑移相应减小,产生相对滑移时的荷载相应增大,r=1.25、r=1.50和r=2.00时3组模型受力全过程中的相对滑移值均接近为0,相对滑移的最大值分别仅为0.54 mm、0.38 mm和0.36 mm。当R4模型(r=0.75)达到荷载(抗弯承载力)6 884.4 kN时,组合梁L/5跨截面相对滑移仅为0.75 mm,由此可知,从相对滑移角度考虑,钢-混凝土组合梁r≥0.75即可满足抗滑移要求。
3.3 破坏模式
屈服栓钉比例与荷载关系曲线如图8所示,纵坐标为各模型中屈服栓钉数量占栓钉总数的比例,数据标记点为该模型屈服荷载。5组模型中均为栓钉最先出现屈服,使栓钉开始屈服的荷载随着r的增大而增大;随着荷载的增大,屈服栓钉的数量不断增多,栓钉全部屈服时的荷载随r的增大而增大。钢梁的屈服首先出现在跨中底板,钢-混凝土组合梁的破坏模式有两种:当0.25≤r<0.75时,钢梁底板屈服发生在栓钉全部屈服之后,且钢梁底板屈服与栓钉全部屈服的荷载差值随剪力连接度的增加而减小;当r≥0.75时,组合梁的跨中钢梁的屈服发生在栓钉全部屈服之前。因此r≥0.75时,组合梁即可符合完全抗剪的设计要求。

图8 屈服栓钉比例与荷载关系曲线
3.4 剪力连接度的取值
本研究共调研统计了国内22座该类桥型在实际工程中与设计通用图纸中的剪力连接度,剪力连接度统计表如表2所示。由表2可知,国内钢-混凝土组合梁的剪力连接度取值较大,取值范围为1.36~2.82。研究可知,r≥0.75时,组合梁的抗弯承载力及弹塑性阶段抗弯刚度基本保持不变,相对滑移接近于0,且组合梁的破坏模式满足完全抗剪设计的要求。国内实际工程中采用的剪力连接度安全系数过高,数量过多的栓钉造成了材料的浪费且会增加工程量。因此综合考虑钢-混凝土组合梁的受力性能和经济性,建议钢-混凝土组合梁的剪力连接度的取值范围为0.75~1.25。
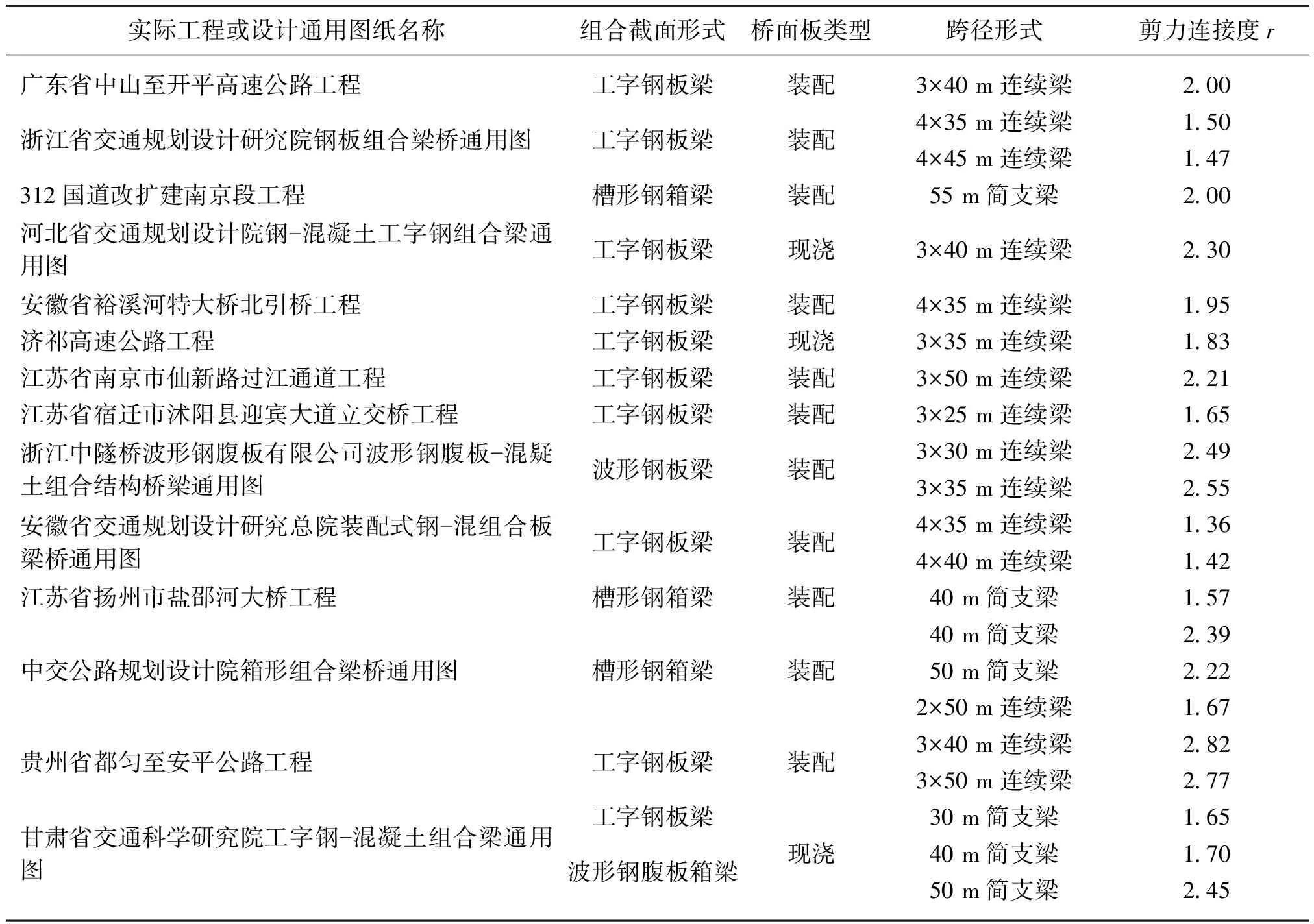
表2 剪力连接度统计表
4 结论
结合所依托工程的设计参数,采用有限元数值模拟的方法,针对不同剪力连接度对槽形钢-混凝土组合梁的受力性能的影响进行参数分析,研究得到以下结论。
(1)当0.25≤r<0.75时,钢-混凝土组合梁的抗弯承载力随r的增大而增大,但增幅不断减小,且弹塑性阶段组合梁抗弯刚度下降较大;当r≥0.75时,抗弯承载力与弹塑性阶段抗弯刚度基本保持不变。
(2)钢-混凝土组合梁相对滑移从支座向跨中呈先增加后减小的分布规律,最大值发生在L/10~L/5跨截面,跨中相对滑移为0。相对滑移的大小与r的大小成反比,剪力连接度越大,相对滑移越小。当r≥0.75时,相对滑移接近为0。
(3)当0.25≤r<0.75时,钢梁底板屈服发生在栓钉全部屈服之后;当r≥0.75时,组合梁的跨中钢梁的屈服发生在栓钉全部屈服之前。当r≥0.75时,钢-混凝土组合梁即可符合完全抗剪的设计要求。
(4)国内该类型桥梁的剪力连接度要求偏于保守,综合考虑结构安全性和工程成本,建议剪力连接度的取值范围为0.75~1.25。
