基于THINC/QQ 格式的超空泡鱼雷三维流场特性及水动力性能优化研究
2022-11-11谢彬杜艳平
肖 腾,谢彬,2,杜艳平
(1.上海交通大学 海洋工程国家重点实验室,上海,200240;2.上海交通大学 船海工程数值试验中心,上海,200240;3.上海交通大学 中英国际低碳学院,上海,201306)
0 引言
自然超空泡是高速航行器周围的流体因压力降低至饱和蒸汽压以下发生相变后形成的较大蒸汽与气体的空腔。当空泡尺度扩张到足以包括整个航行器时,就形成超空泡。借助超空泡技术,苏联研制出了“暴风”(Shkval)超空泡鱼雷,使航速提高至200 kn 以上,受到国内外学者的广泛关注。资料表明[1],水下航行器在有几乎完全包覆表面的稳定超空泡的条件下,仅有头部空化器直接与水体接触,航行器所受到的粘性阻力与压差阻力显著降低,相较于全湿流动,总阻力可降低1~2 个数量级。
对于超空泡的发展与机理,许多学者都做了相关的研究工作。Ahn 等[2]进行了多组水洞实验,系统地分析了超空泡的形态与几种常用空化器头型的关系。Saranjam[3]对水下移动物体的超空泡流动进行了数值仿真和实验研究,数值预测与实验结果高度一致。贾立平等[4]进行了自然超空泡高速弹射实验,研究了超空泡的形成过程和空化器参数对超空泡临界空化数的影响,并分析了超空泡形态与空化器的关系。王瑞等[5]使用高速水洞实验平台研究了4 种不同形状空化器对绕回转体超空泡特性的影响,给出了相同工况下空化器头型与空泡尺寸和阻力特性的关系。
然而,超空泡实验装置耗资较高,且实验中的介入式装置会对空泡流场产生严重干扰。随着空化理论和计算方法的不断发展,数值仿真方法逐渐成为超空泡问题的重要研究手段。齐江辉等[6]基于雷诺平均类(Reynolds-Averaged Navier-Stokes,RANS)模型对无尾翼超空泡鱼雷模型开展了超空泡流仿真,分析了不同空化数和各种圆盘空化器的改型对超空泡形态和减阻效果的影响。Kim 等[7]通过改变空化器形状和开角,仿真研究了直航超空泡鱼雷的空化器优化设计方法,给出一定工况下的空化器最优解并进行了拖曳实验验证。李雨田[8]通过仿真计算,得到了空泡外形随空化数和攻角的变化趋势,分析了航行器流体动力特性变化,并给出了影响其变化的相关因素。赵潇雨等[9]使用FLUENT 软件对4 种典型空化器头型进行了超空泡数值仿真研究,分析了自然超空泡尺寸与空化器形状、尺寸和空化数之间的关系。除了改变空化器形状,在材料表面涂覆亲疏水性涂层可实现流动减阻。黄超等[10]实验研究了表面亲疏水性对小球入水后空泡的影响,其结果显示,超疏水表面的小球由于表面液膜很快产生流动分离,相比于亲水表面的小球更易于空泡的产生。不过,表面亲疏水性对鱼雷超空泡的影响还有待进一步研究。
不同于此前基于商业软件的数值仿真研究,文中基于THINC/QQ 方法,利用剪切应力传输(shear stress transport,SST)k-ω湍流模型和Schnerr-Sauer空化模型在开源软件OPENFOAM 上开发了基于非结构网格的不可压缩空化流求解器,对超空泡鱼雷的三维流场特征进行了数值仿真研究,并用经验公式对仿真结果的可靠性进行了验证。在此基础上分析讨论了不同空化数、空化器形状以及鱼雷表面浸润性对超空泡特征和水动力性能的影响规律。
1 数值模型
1.1 多相流控制方程
文中基于流体体积(volume of fluid,VOF)函数多相流模型,假设将整个空化流动流场中的气液两相视为一种混合均质,共享速度场、压力场和湍流参数,统一求解Navier-Stokes 方程


式中:u为速度;p为修正压力;µ为流体的动力粘度;φ为液相流体所占的体积分数;为气液两相间的质量传递率;F=σκ∇φ为表面张力项,其中σ=0.072为表面张力系数,κ=∇·为单位向量的散度,n=∇φ为体积分数的梯度。
汽液两相通过体积分数值平均得到混合均质的粘度µ和密度ρ,且
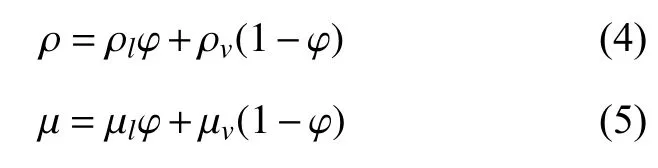
式中:ρl和 µl分别为水的密度和粘度;ρv和 µv分别为水蒸气的密度和粘度。
1.2 VOF 自由界面捕捉方法
为了更好地捕捉超空泡形态,该研究采用VOF高精度算法THINC/QQ[11]。该方法采用双曲正切函数重构网格单元内的自由界面,对于三维情况,双曲正切函数为

式中,β是用于控制界面过渡区域厚度的参数。界面方程Pi(x,y,z)+di=0为2 次多项式

式中:cstr(s,t,r=0,1,2,s+t+r≤2)为控制界面形状的参数,由界面的单位法向量和曲率确定;(xc,yc,zc)为 网格的重心。系数cstr确定后,式(6)中仅有确定界面位置的系数di未知,可根据目标网格的VOF函数均值求解
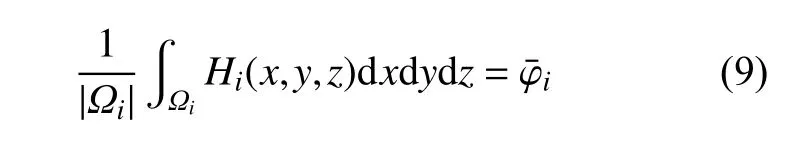
式中:双曲正切函数H的网格积分平均值可以用数值积分点近似;系数di通过Newton-Raphson 方法计算,然后求解以下方程更新VOF 函数

式中,下标iup代表边界面上游方向的网格单元。
1.3 湍流模型
由于超空泡流动具有很高的雷诺数和非定常特性,所以文中引入了SSTk-ω湍流模型求解RANS方程。SSTk-ω模型是由Menter[12]提出,结合了kω模型和k-ε模型的近壁面和远壁面区域,被广泛地用于超空泡流动仿真中。该模型中的湍动能k和比动能耗散率ω的计算方法如下

式中:Γ,σk,σω,β,β*是模型常数;混合函数F1为
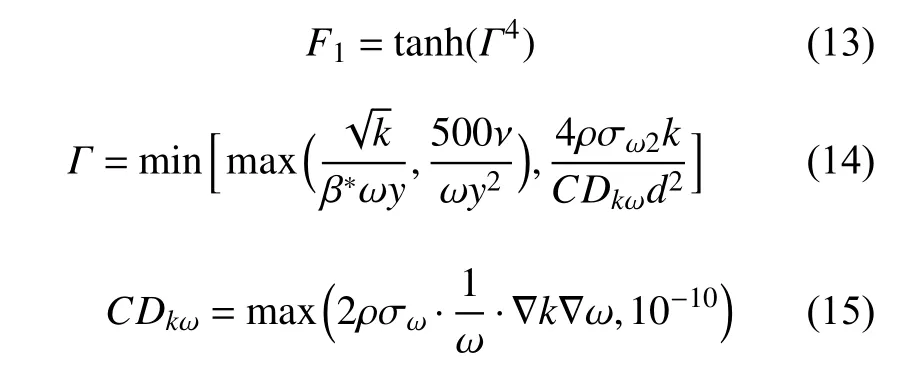
涡黏系数定义为
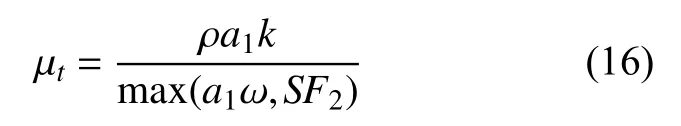
式中:a1=0.31;混合函数F2定义为

1.4 空化模型
由于空化流动相比全湿流动存在着相变现象,要对其中的质量传递过程进行准确仿真,就要引入空化模型。在OPENFOAM 中,式(2)中的质量传递源项被分解为蒸发和液化过程的分量

式中,和m˙-分别为液化和蒸发过程的质量传递率。
此处使用了Schnerr-Sauer 空化模型[13],其质量传递源项是由Rayleigh-Plesset 方程推导而来,其源项方程如下
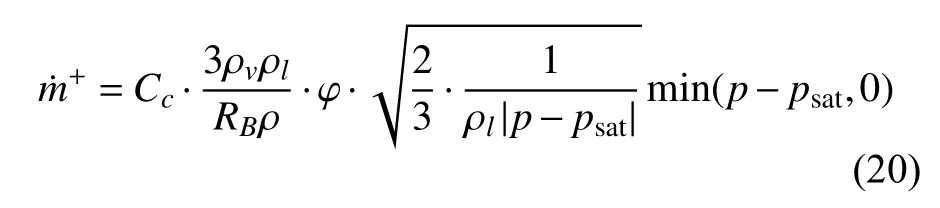

式中:Cc和Cv为方程系数,默认推荐值均为1;φnuc为数值成核项,用以在计算中初始化空化过程;psat为饱和蒸汽压;RB为气泡半径。
为了兼顾计算精度和效率,文中采用具有时空2 阶精度的有限体积法对控制方程进行离散。其中时间推进采用2 阶龙格-库塔方法,对流项和扩散项分别用Van Leer 格式(迎风格式)和线性格式,速度-压力耦合则采用PISO(pressure implicit with splitting of operator)算法。时间步长设为自适应,满足最大库朗数为0.3 的条件。
2 计算模型
2.1 超空泡鱼雷外形
文中使用的计算模型参考Serebryakov 给出的无尾翼鱼雷模型[14]。该模型是超空泡航行器数值仿真研究中被广泛使用的模型之一。文中的超空泡鱼雷模型由前部空化器、锥体头段、平行中段和尾部喷管组成,其尺寸根据“暴风”(Shkval)超空泡鱼雷做了优化,旨在给出更贴近真实尺度的数值仿真结果,其总长3.28 m,直径0.2 m,圆盘空化器直径0.08 m,具体的外形和尺寸参数如图1 所示。
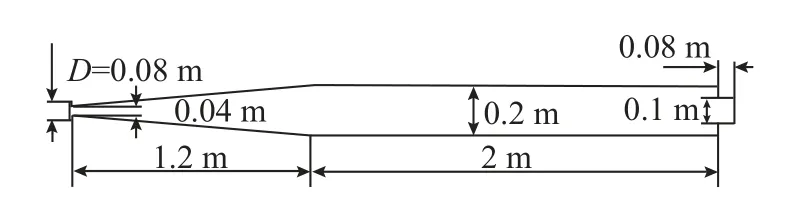
图1 超空泡鱼雷模型外形尺寸示意图Fig.1 Shape and dimensions of the supercavity torpedo model
2.2 计算域与网格划分
计算域及网格示意图如图2 所示。计算域总长度为60D,高度和宽度为20D,近壁区域进行网格加密,向流场边界逐渐稀疏。边界条件设置如下:入口为速度入口条件,流速按照空化数(σ=(p-psat)/(0.5ρlu2))来设定;出口为压力出口条件,按照水深10 m 设置;鱼雷表面为壁面条件。研究表明[15],航行器形成自然超空泡的条件是空化数σ ≤0.1,选取45~95 m/s 范围内的多组航速,对应空化数范围为0.0965~0.2160 进行计算。如表1 所示,计算前使用多组不同疏密程度的网格进行网格收敛性测试。表1 对比了不同计算网格得到的空化数 σ=0.0270条件下鱼雷模型的超空泡尺度数据。对比结果显示,较为粗糙的网格1 与网格2 得到的数值结果收敛性差,与其他网格的差距较大;网格4 较网格3 进一步加密,得到的超空泡尺度结果变化很小。在确保结果收敛性的基础上兼顾计算效率,选取网格3 的174 万网格用以后续计算。

图2 计算域及网格划分示意图Fig.2 Diagram of computational domain and mesh

表1 超空泡尺度网格收敛性测试Table 1 Mesh convergence test on the supercavity scale
2.3 浸润性边界条件
超疏水表面特征是通过设置鱼雷表面的边界条件实现的。如图3 所示,基于超疏水表面的宏观滑移特点,使用部分滑移边界条件。根据接触角给定滑移长度,滑移速度us与滑移长度Ls的关系式为
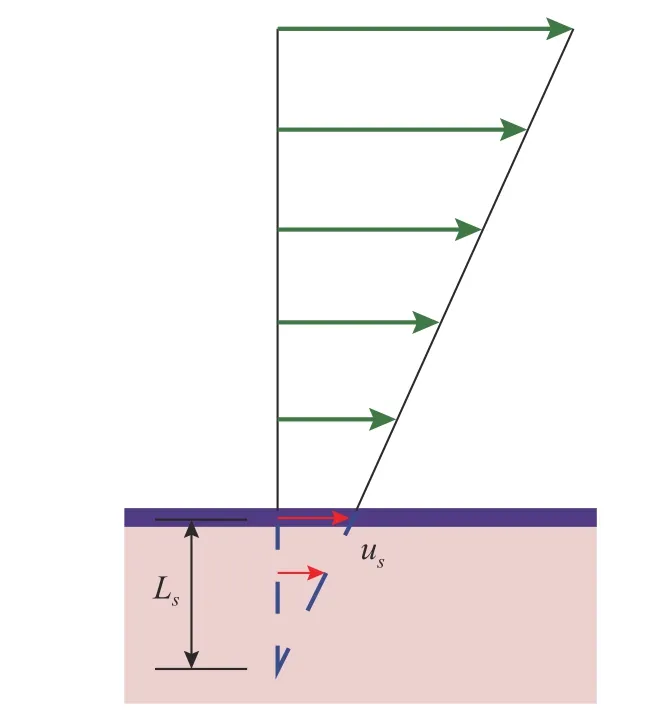
图3 部分滑移边界条件Fig.3 Boundary conditions of partial slip

式中,Ls根据Zhang[16]的统计数据确定,接触角θ=160°时Ls=2.2。接触角是衡量材料亲疏水性的重要指标(见图4)。
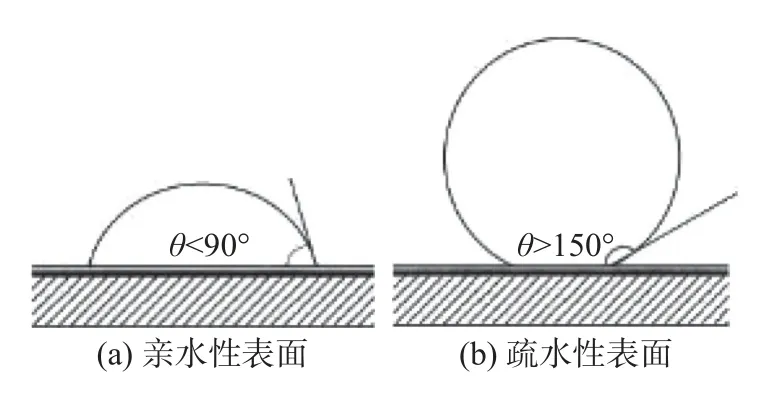
图4 接触角与亲疏水性的关系Fig.4 Relation between contact angle and hydrophobicity
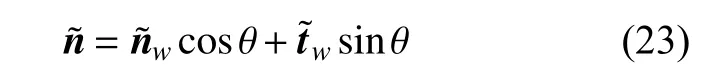
2.4 计算模型验证
文中选取了1 组经典锥形空化器的案例进行模型验证。在同样的工况下,文中数值仿真空泡结果与Javadpour 等[17]的水洞实验结果的对比如图5 所示。图中给出了2 组不同速度下的稳定空泡形态,每组上方是文中的数值仿真结果,下方是实验结果。从图中可以看出,在不同速度对应的不同空化数条件下,该计算模型对空泡尺度的变化规律预测与实验结果一致。对空泡长度进行测量和比较发现,数值仿真得到的空泡长度与实验结果相差5%以内。文中的数值仿真结果与实验结果的吻合度较高,说明文中的计算模型可以很好地对超空泡流动进行仿真。

图5 空化器后空泡形态数值仿真结果与实验结果对比Fig.5 Comparison of the cavity behind the cavitator between experimental results and the numerical results
3 仿真结果分析
3.1 自然超空泡演化过程
图6~图8 分别给出了3 组不同空化数工况下的空泡形态演化过程。图6 为 σ=0.0646工况下空泡形态演化,对应流速为55 m/s,此时鱼雷模型并不能产生完整的超空泡,头部空泡发展至肩部后即为此空化数下的稳定状态。图7 为σ=0.0399工况下空泡形态演化,对应流速为70 m/s,此时鱼雷模型可以产生长度与模型接近的超空泡,模型的超空泡临界空化数即σ ≈0.04。图8 为σ=0.0270工况下典型的自然超空泡演化过程,由图可见,自然超空泡在演化过程中呈现以下特点:在空化初始阶段,仅有空化器末端和尾段末端存在规模较小的空泡;随着空化数降低,锥体头端和平行中段连接处的肩部也产生了肩部空泡;3 处主要空泡随着空化数降低长度将继续增加,直至互相融合;融合后的超空泡体积将继续增长,直至稳定。

图6 σ=0.0646工况下超空泡形态演化过程Fig.6 Evolution process of supercavity shape at σ=0.0646

图7 σ=0.0399工况下超空泡形态演化过程Fig.7 Evolution process of supercavity shape at σ=0.0399

图8 σ=0.0270工况下超空泡形态演化过程Fig.8 Evolution process of supercavity shape at σ=0.0270
值得注意的是,在前方空泡与后方空泡融合的过程中,会发生后方空泡体积缩小、部分溃灭的现象。图9 为空化数 σ=0.0399时头部空泡与肩部空泡融合时肩部空泡及压力分布图。此时,头部空泡闭合区末端存在高压区,随着头部空泡的发展,此高压区逐渐靠近肩部空泡,导致其局部液化,体积收缩,直至与前方空泡完全融合后继续向后发展。主空泡发展至尾段附近时末端的高压区同样会在与尾部空泡融合过程中抑制其发展。

图9 局部空泡融合位置压力分布Fig.9 Pressure distribution at the position of partial cavity fusion
图10 给出了空化数 σ=0.0399时临界超空泡流动过程中鱼雷的水动力系数随时间发展的曲线。从图10(a)的阻力系数CD曲线中可以看出,在超空泡形成的初期,航行器所受阻力较高,根据数值仿真初始条件及数值结果,空泡在前2 ms 迅速发展,峰值可视为鱼雷模型在当前航速下的理想全湿流动阻力;随着超空泡的发展,航行器所受阻力显著降低;直至稳定的超空泡流形成后,航行器的阻力系数也降低至一个稳定值,相比超空泡产生初期的峰值减少了88%。图10(b)中的升力系数CL在超空泡的初生期,由于空化器后部、弹体肩部和尾部有着局部空泡的产生,在此类扰动和近壁区域流场的综合影响下有着短暂的波动,但幅度较小;在超空泡的发展趋于稳定之后,无尾翼航行器升力值几乎为零,不再受升力影响。

图10 超空泡航行器水动力系数时历曲线Fig.10 Time-history curves of hydrodynamic coefficients of supercavity vehicle
3.2 超空泡形态验证
为了验证文中所使用的求解器在超空泡数值仿真方面的准确性,将所得的空泡特征长度和特征直径(其中超空泡尺度量取方式如图11 所示)与Reichardt 和Logvinovich 经验公式[18-19]进行对比验证。这些经验公式都是由势流理论推导而来,适用于小空化数下的超空泡形态计算。

图11 超空泡尺度测量Fig.11 Measurement of supercavity scale
Reichardt 经验公式主要将空泡特征尺度与空化数和阻力系数联系起来,即
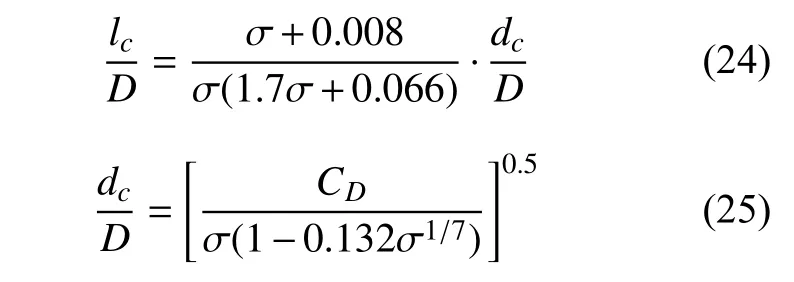
式中:lc和dc分别为空泡的长度和直径,其量取方式如图11 所示;CD为阻力系数,由以下半经验公式计算得到

式中,CD0是 σ=0时的阻力系数,根据实验数据推算得出,根据Self 和Ripken[20]的推导,对于文中的圆盘空化器,取CD0=0.80。
Logvinovich 经验公式也尤其适用于小空化数,特征尺度与空化数的关系为

式中,a和k为经验常数,文中分别取值为2.0 和0.95。
取空化数 σ=0.0270为例,将文中的超空泡形态的数值仿真结果与上述经验公式进行比较,结果如表2 所示,其中相对误差R和相对误差L分别对应与Reichardt 公式和Logvinovich 公式的对比结果。如表所示,文中数值仿真结果中的超空泡尺度与经验公式结果较为接近,验证了文中数值方法对鱼雷模型超空泡尺度预测的可靠性。其中,空泡特征长度相对误差分别为3.32%和2.56%,空泡特征直径相对误差分别为3.17%和4.08%,误差较低。误差来源主要是基于势流理论的经验公式没有考虑流体粘性。

表2 超空泡尺度数值结果验证Table 2 Validation of numerical results of supercavity scale
3.3 空化器形状尺寸对超空泡的影响
圆盘形是空化器最常见的形状,其形状简单,效果明显。此外,还给出几种不同形状尺寸的空化器改型。各型空化器外形如图12 所示,其中(a)型为前文所使用的D=0.08 m的圆盘空化器;(b)型为D=0.12 m的圆盘空化器;(c)型和(d)型为锥度不同的D=0.08 m的锥头空化器;(e)和(f)型为球面半径分别为 0.04 m 和 0.05 m,截面基圆直径都是D=0.08 m的球面空化器。

图12 不同空化器头型几何模型Fig.12 Models of cavitators with different head shapes
表3 给出了航速u=90 m/s,空化数σ=0.0241时不同头型空化器模型在超空泡稳定阶段的阻力系数值。由于外形平滑,没有尖端高压区,使用小球面半径球面空化器模型在超空泡阶段所受阻力最小,使用小锥角高锥度的锥体空化器次之;使用2 个不同直径的圆盘空化器模型所受阻力最高,且阻力值大小与空化器直径成正比。

表3 不同空化器超空泡阶段阻力系数Table 3 Drag coefficients for different cavitators at the supercavity stage
使用不同头型空化器模型的超空泡轮廓如图13 所示。(b)型较大直径的圆盘型空化器能够产生最大体积的超空泡;而(e)型半球面型空化器由于边缘切向角度不能更好地分离流动,产生的超空泡最细也最短。综合表3 的阻力系数结果,超空泡的体积尺寸与鱼雷模型所受阻力成负相关关系。
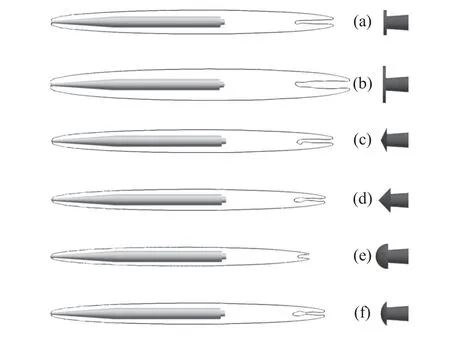
图13 不同空化器产生的超空泡轮廓Fig.13 Contours of supercavity generated by different cavitators
总的来说,扁平比和直径较大的空化器更容易产生更大体积的稳定超空泡,但是鱼雷模型在超空泡稳定阶段所受的阻力也更大;使用长径比和锥度较大、直径较小的空化器的鱼雷模型在超空泡阶段所受的阻力更小,但是会在一定程度上损失超空泡的体积。从超空泡减阻的角度考虑,后一类空化器选型方向更利于超空泡鱼雷的高速减阻。在实际应用中,需要平衡空化体积与航行阻力之间的关系,空泡体积过小会导致空泡无法完整包覆航行器,从而不能达到减阻效果。
3.4 表面亲疏水性对超空泡的影响
为研究表面浸润性对超空泡的影响,文中选取了上文(e)型半球空化器的鱼雷模型,分别设定弹体及空化器表面材质具有超疏水性质(接触角θ=160°)和超亲水性质(接触角 θ=20°)。
图14~图16 分别给出了不同空化数工况下的超疏水表面与亲水表面的鱼雷模型的阻力系数以及组分里的粘性阻力系数CV曲线。在空化数σ=0.0965工况下,鱼雷模型并不能产生完整包覆表面的超空泡,而仅在鱼雷头部产生周期性脉动的局部空泡(见图6),也造成了图14(a)中50~60 ms 阶段的阻力值波动。超疏水表面整体可降低航行阻力30%左右。而且由图14(b)可见,全弹体覆盖的超疏水表面较亲水表面在此工况下可以降低粘性阻力约80%。在空化数 σ=0.0399工况下,超空泡能够完整包覆鱼雷表面,总阻力特别是粘性阻力的下降更为明显。

图14 σ=0.0965工况下不同接触角鱼雷阻力系数曲线Fig.14 Drag coefficient curves of torpedoes with different contact angles at σ=0.0965

图15 σ=0.0399工况下不同接触角鱼雷阻力系数曲线Fig.15 Drag coefficient curves of torpedoes with different contact angles at σ=0.0399

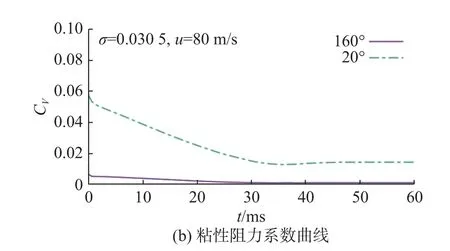
图16 σ=0.0305工况下不同接触角鱼雷阻力系数曲线Fig.16 Drag coefficient curves of torpedoes with different contact angles at σ=0.0305
随着航速增加,在空化数 σ=0.0305工况下,在空化初期的前20 ms 内,超疏水表面可以降低阻力20%以上。随着空泡体积扩大,鱼雷模型所受阻力中粘性阻力占比减小,阻力差值稳定在10%左右。由图15(b)的阻力系数曲线可见,超疏水表面从流动初期就保持了很低的粘性阻力水平。在超空泡流动开始阶段,超疏水表面模型所受粘性阻力较亲水表面模型低约90%;随着空泡发展,亲水表面模型与水接触面积减小,粘性阻力也逐渐减小。综合图14~图16 来看,随着航速提高,空化数降低,产生的空泡包覆鱼雷弹体的面积也更大,超疏水表面减阻效果会有所下降。从减阻幅值的角度衡量超疏水表面鱼雷,控制航速与压力条件以达到临界空化数的效果更为明显。
图17 为分别使用2 种亲疏水表面的(e)型空化器鱼雷模型在超空泡初期的超空泡形态。图17(1)~(5)分别是空泡从空化器末端初生到发展长大过程中5 个时刻对应的形态。超疏水表面鱼雷模型产生的空泡长度均略长于同时刻的亲水表面鱼雷模型,即超疏水表面鱼雷模型可以更快地产生空泡,这一点对于实际应用十分有利。根据相关数值结果,超疏水表面鱼雷模型还可以产生更大体积的空泡,其头部空泡长度较亲水表面鱼雷长约5%,这是因为超疏水的表面特性,超空泡更易附着在弹体表面(见图17(3)~(5)),而亲水表面鱼雷模型与空泡间存在一层水膜(见图17(1)~(2))。随着空泡发展,由于其闭合区末端的逆压力梯度产生的回射流将持续存在于弹体与空泡之间,受到表面疏水性的影响,超疏水鱼雷表面产生的回射流长度远小于亲水表面鱼雷所产生的(见图17(5)),这有利于超空泡的稳定发展和航行器的持续减阻。图18 给出了图17(5)时刻2 种鱼雷的速度场。从图18(b)可见,亲水表面鱼雷的弹体肩部由于壁面效应存在速度更低的区域,肩部空泡的体积相较于疏水表面鱼雷更小。
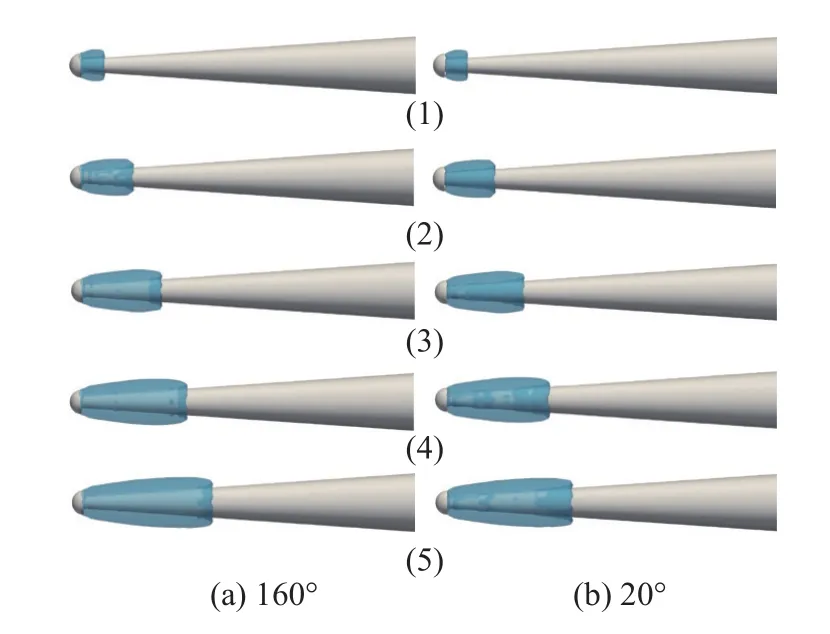
图17 2 种鱼雷在超空泡初期不同接触角下的头部空泡形态Fig.17 Frontal cavity shapes of two kinds of torpedoes with different contact angles at the initial supercavity stage

图18 2 种鱼雷在超空泡初期不同接触角下的速度场Fig.18 Velocity field of two kinds of torpedoes with different contact angles at the initial supercavity stage
考虑到工程应用实际情况,还研究了超疏水表面材料在鱼雷表面不同部位使用的减阻和空泡优化效果的区别。如图19 所示,将(e)型空化器鱼雷模型在轴向划分为4 个部分:空化器(a)、前段(b)、中段(c)和尾段(d),分别单独使用超疏水表面进行计算。
一是水资源供需矛盾突出。我国水资源总量位居世界第六,但人均水资源量仅为世界平均水平的1/4。经济的持续高速或较高增长,人口增长及人均消费水平的持续提高,使得供需矛盾突出,给水安全带来了日益沉重的压力,且这种压力在相当长时间内是不可逆转的。

图19 使用超疏水表面的位置(红色为超疏水表面)Fig.19 Positions of superhydrophobic surfaces employed(red color indicates superhydrophobic surfaces)
图20~图21 分别给出了4 种在不同位置布置超疏水表面的鱼雷在空化数 σ=0.0305工况下的阻力系数和粘性阻力系数曲线。在弹头与中段的结合区域布置超疏水表面减阻效果最明显,尾段次之;在头部和锥体前端布置超疏水表面减阻效果最不明显。随着超空泡的发展,阻力值差距缩小。在中段结合区域布置超疏水表面对不同阻力成分的降低效果最明显;图21 中10 ms 后尾段对粘性阻力相较中段降低更明显,是因为肩部空泡覆盖了一定面积的弹体。空化器与锥体前端布置超疏水表面对空化初期阻力的降低效果相似,考虑到表面积的差别,在空化器上使用超疏水表面相比锥体前段综合效果更好。
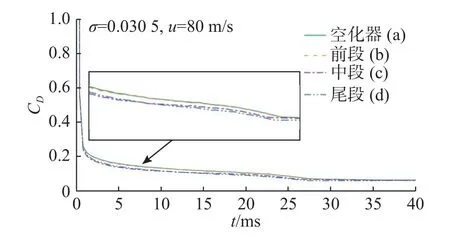
图20 不同超疏水位置鱼雷阻力系数曲线Fig.20 Drag coefficient curves for torpedoes with superhydrophobic surfaces at different positions

图21 不同超疏水位置鱼雷粘性阻力系数曲线Fig.21 Viscous drag coefficient curves for torpedoes with superhydrophobic surfaces at different positions
4 结束语
基于THINC/QQ 方法,SSTk-ω模型以及Schnerr-Sauer 空化模型,在OPENFOAM 平台建立三维空化流动求解器,经过与实验结果对比验证后,对无尾翼鱼雷模型在不同速度、空化器形状以及弹体表面浸润性工况下开展了三维超空泡流动数值仿真研究和水动力性能分析,获得以下结论。
1) 随着空化数不断降低,鱼雷超空泡的演化过程有着明显的规律,在空化数达到超空泡临界值 σ=0.04时,稳定包覆鱼雷弹体的超空泡可以使航行阻力下降88%左右。从自然超空泡的演化机理的角度考虑,适当提高航速以保持更稳定和更大体积的超空泡有利于降低航行阻力。
2) 大长径比、高锥度的空化器有利于超空泡鱼雷的减阻,但是会损失超空泡体积。从空化器选型的角度考虑,在减阻以提高航速的同时,也要保证超空泡的尺寸。
3) 超疏水表面可以明显降低超空泡鱼雷在空化初期的航行阻力,尤其是粘性阻力成分,特别是在临界空泡数工况下。同时,超疏水表面可以加快初始空泡的产生,空泡发展过程中更易于附着在超疏水表面,抑制了空泡内液膜和回射流,有利于提高超空泡的稳定性。
后续的研究工作将基于文中的数值模型,拓展研究通气超空泡与超疏水技术的应用。
