浮式海水淡化装置系留系统水动力分析

李家豪,陈沛宏,张大朋,严谨,朱克强

(1.广东海洋大学船舶与海运学院 湛江 524088;2.宁波大学海运学院 宁波 315211)

0 引言

某海洋浮式海水淡化装置可为海上来往船只供给淡水,为保证工作安全,必须对其系留系统进行动力分析。为分析此装置的系留系统,本研究通过相关参数建立数学模型进行仿真模拟和数值计算。该系留系统的系缆在风、浪和流的联合作用下不断进行张紧和松弛的交替运动,系缆所承受的载荷是非线性的,此外海洋环境中的很多复杂影响要素是随时间变化的,因此对系缆的动力分析采用非线性的时域耦合分析。在分析时不考虑系缆的扭矩和弯矩,使用凝集质量法[1]建立缆线的质量-弹簧模型。利用水动力软件OrcaFlex建立数学模型后,分析系缆的动力特性,确定系缆受力,期望为系留系统中系缆的设计和建设提供参考。

1 基本理论

1.1 系留张力的计算原理和动态分析

对缆线先后进行静态分析和动态分析。其中,静态分析的主要目的有2个:①在重力、浮力和流体水动力等载荷的共同作用下,确定系留系统的平衡构型;②为动态仿真提供初始构型。在静态分析中,采用效率高且较有效的悬链线法计算缆线的平衡位置,计算时忽略缆线的弯曲刚度、扭转刚度和缆线端点处的作用力。

动态分析可在指定时间段内对模型运动进行实时模拟,其起始位置由静态分析推导得出。OrcaFlex软件在动态分析中使用的运动公式为:

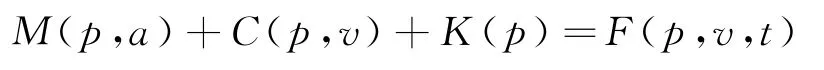
式中:M(p,a)表示系统的惯性负载;C(p,v)表示系统的阻尼力;K(p)表示系统的刚度载荷;F(p,v,t)表示外载荷;p、v和a分别表示位置、速度和加速度矢量;t表示模拟时间。

非线性动力学问题通常采用显式或隐式求解方法。其中,显式求解法包括恒定时间步的前向欧拉法,求解时没有收敛性问题,也无须求解联立方程组;隐式求解法可采用广义-α积分法[2],其运动方程的求解是一系列相互关联的非线性方程的求解,这个求解过程须通过迭代和联立方程组才能实现。隐式求解法的最大优点是具有无条件稳定性,即时间步长可以任意大。

通过凝集质量法建立缆线的动力分析模型可大大简化数学公式和提高计算效率。缆线凝集质量的有限元模型就是将缆线分成一系列无质量的线段,线段的每个端点是1个有质量的节点,在这些线段上只能模拟缆线的轴向性能和抗扭性能,其他性能(如质量、重力和浮力)都集中于质量节点上。在这种方法中,水下缆线模型可被视为一系列无质量线弹性单元连接和质量集中在节点上的集中质量-弹簧离散模型,缆线上的张力通过应力-应变关系按节点间的瞬态位置经计算求得。较完整的缆线结构模型可用3种弹簧+阻尼器表示其性能,分别是轴向弹簧+阻尼器、弯曲弹簧+阻尼器以及扭转弹簧+阻尼器(图1)。

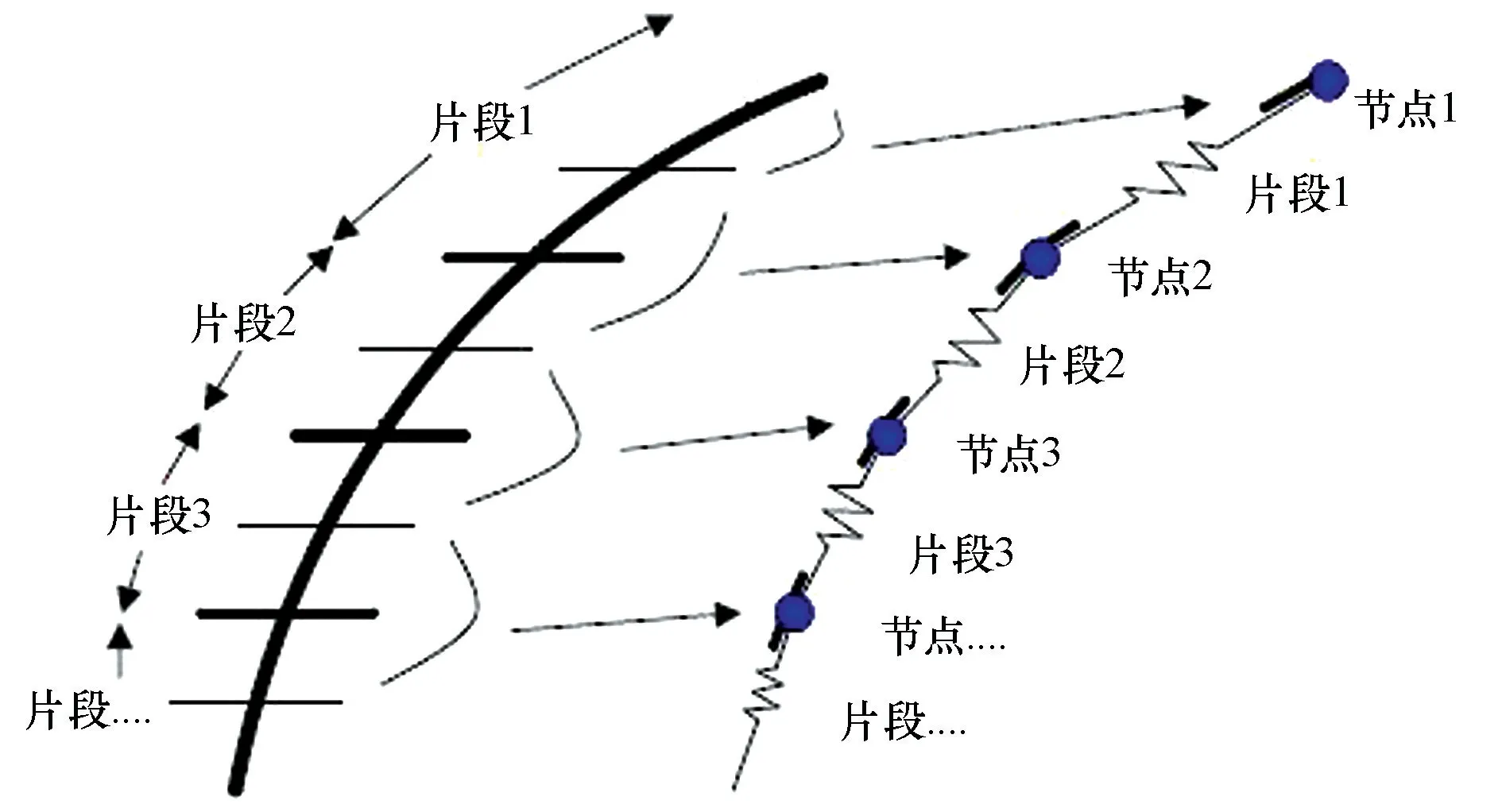
图1 缆线结构模型

对缆线进行分析计算时,每个节点承受2个方向上的张力、弯曲力矩、剪切力和扭转力矩,节点上的总载荷就是这些结构载荷与其他非结构载荷(如重力、拖曳力和附加质量)的矢量和。假定缆线为挠性结构,不传递扭矩且无弯曲力矩。如果缆线的轴向刚度是线性的,则张力矢量的计算公式为:

式中:T e表示有效张力;T w表示壁面张力;EA表示缆线轴向刚度;ε表示轴向平均应变,其值为(L-λL o)/(λL o),λ表示单位分段的膨胀系数;L表示某时刻缆线结构模型受力后的单位分段长度;L o表示单位分段的原长;v表示泊松比;P i和P o分别表示缆线内、外压力;A i和A o分别表示内、外截面面积,对于缆线来说A i=0;e表示缆线的阻尼系数。

1.2 环境载荷

波浪可被视为由多个振幅不同、频率不同和相位杂乱的单元波叠加而成,本研究利用谱分析来研究具有平稳随机过程的波浪的统计特性。利用“北海联合海浪计划”(JONSWAP)谱对波浪进行设定,该谱的优点之一在于引进峰提升因子来描述波浪的成长状态[3]。JONSWAP谱的计算公式为:

式中:a表示无因次常数,通过指定有效波高和波浪周期得出;f表示波浪频率;f m表示波峰频率;g表示万有引力常数;γ表示谱峰提升因子,取平均值;b表 示γ的 因 次 方,且b=exp[-1/2σ2(f/f m-1)2];σ表示波浪能因子,随波浪频率改变而改变,当f≤f m时σ1=0.07,当f＞f m时σ2=0.09。

在实际中,海流的方向和大小随深度的变化而变化。在建立模型时,假定模型所在海况中的静水面处流速较小,则可采用线性内插法指定从海床至海面的流速,并设定海流的方向不随深度变化而变化。以海平面上的某点为坐标原点,水深h处流速的计算公式为:

式中:Vsurface表示海平面处的流速;Vseabed表示海床处的流速;H表示总海水深度。由于坐标原点在海平面上,H和h均为负值。

根据石油公司国际海事论坛(OCIMF)[4]的相关规定,计算时采用的风速通常是静水面上10 m处的风速。在计算风对海工设备的作用时,通常认为风是单向的。

2 模型建立

该模型的坐标系分为全局坐标系和局部坐标系,所有坐标系均使用右手定则,风、浪和流的方向和速度都是相对于全局坐标系的。坐标系中的向量方向根据向量在x-y平面的投影与x轴的夹角(azimuth)以及向量与z轴的夹角(declination)2个角度确定。浮式海水淡化装置模型如图2所示。

图2 浮式海水淡化装置模型

该模型的系泊方式采用悬链式浮筒系泊(CALM),有3根系缆,其外形为弯曲的悬链线,相互之间成120°角对称分布。系缆上端集中于顶端系缆,此系缆的顶端又与浮筒相连。浮筒主要为装置提供浮力和稳定性,同时容纳各种各样的零部件。系缆由锚链与合成纤维系缆组成,其中锚链的成本较低、强度高且伸长率低,而合成纤维绳的使用可减小系缆对平台向下的拉力,从而使平台有更大的有效载荷,在浮力减小的同时减小波浪和海流对平台的作用力[5]。锚链与海底水平相接,系锚点只受水平方向的力,系缆的回复力由其自重产生。悬挂的浮筒可提升系缆,使其免受海底障碍物的影响,且降低模型的垂向载荷。

模型建立与分析的程序如图3所示。

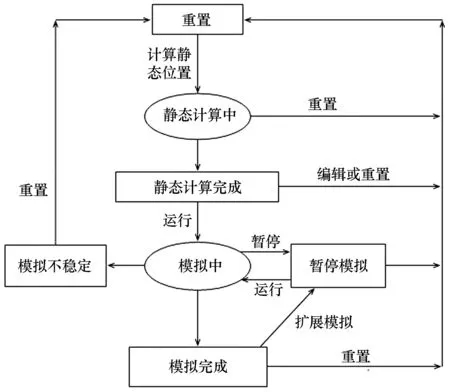
图3 模型建立与分析的程序

在本模型中,采用6D浮标构建浮式海水淡化装置的主体结构,其基本参数如表1和表2所示。

表1 装置上部主体构件参数

表2 缆线的基本参数

设定水深为220 m,JONSWAP谱的参数包括:H z=10 m,T z=13 s,α=0.004 2,σ1=0.07,σ2=0.09,f m=0.059 8 Hz,γ=3.30。模型中关于海流的参数包括:静水面流速为1.000 m/s,海床处流速为0.450 m/s,流速方向为150°。模型中关于风的参数包括:空气密度为0.13 te/m2,空气运动黏性为15E-6 m2/s,平均速度为35 m/s,风向为210°。

3 结果分析

当模拟时间t为-100～3 600 s时,3根系缆的有效张力和曲率分别如图4和图5所示。

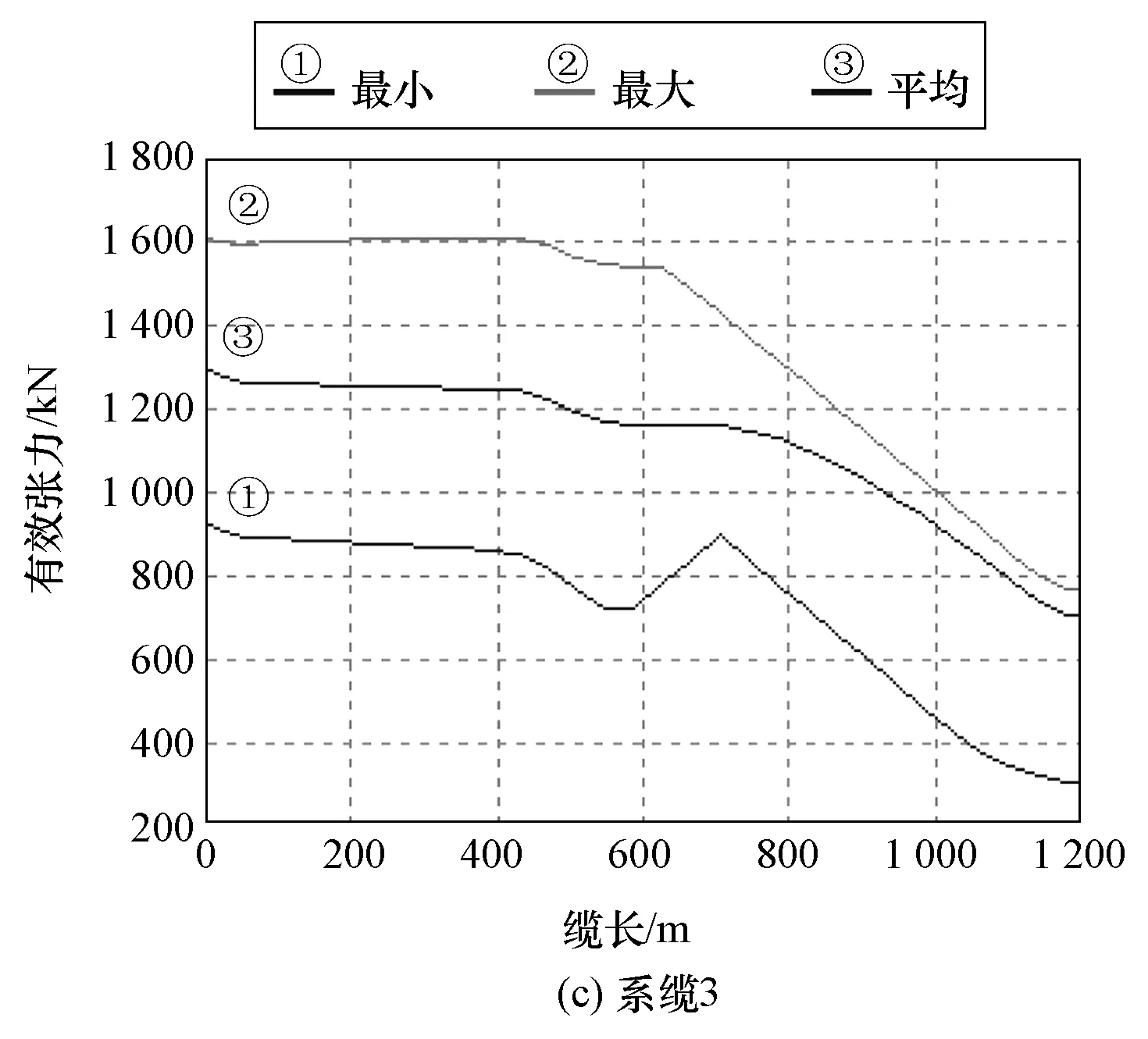
图4 系缆的有效张力

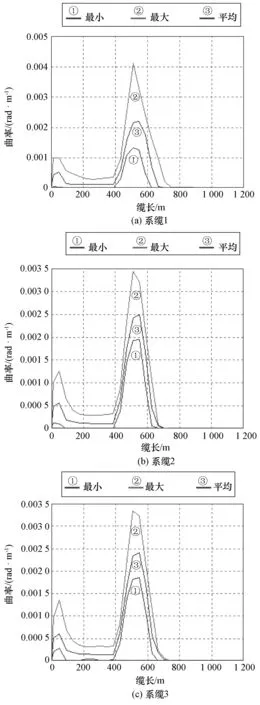
图5 系缆的曲率

系缆1在曲率剧烈变化之前,有效张力随着缆长的增加变化很小;在曲率剧烈变化之时,有效张力开始加剧变化,其中最大有效张力快速变小,平均有效张力缓慢变小,最小有效张力快速变大;当曲率变化趋于0且曲率也趋于0时,随着缆长的增加,最大有效张力继续变小,平均有效张力缓慢变小,最小有效张力继续变大。

系缆2和系缆3的有效张力随着缆长增加的变化趋势大致相同:在曲率剧烈变化之前,最大、平均和最小有效张力均缓慢变小;在曲率剧烈变化之时,最大、平均和最小有效张力均快速变小;在曲率变化之后,最大、平均和最小有效张力均快速变小,且变小趋势大致相同。

3根系缆和顶端系缆端点A处的有效张力如图6所示。

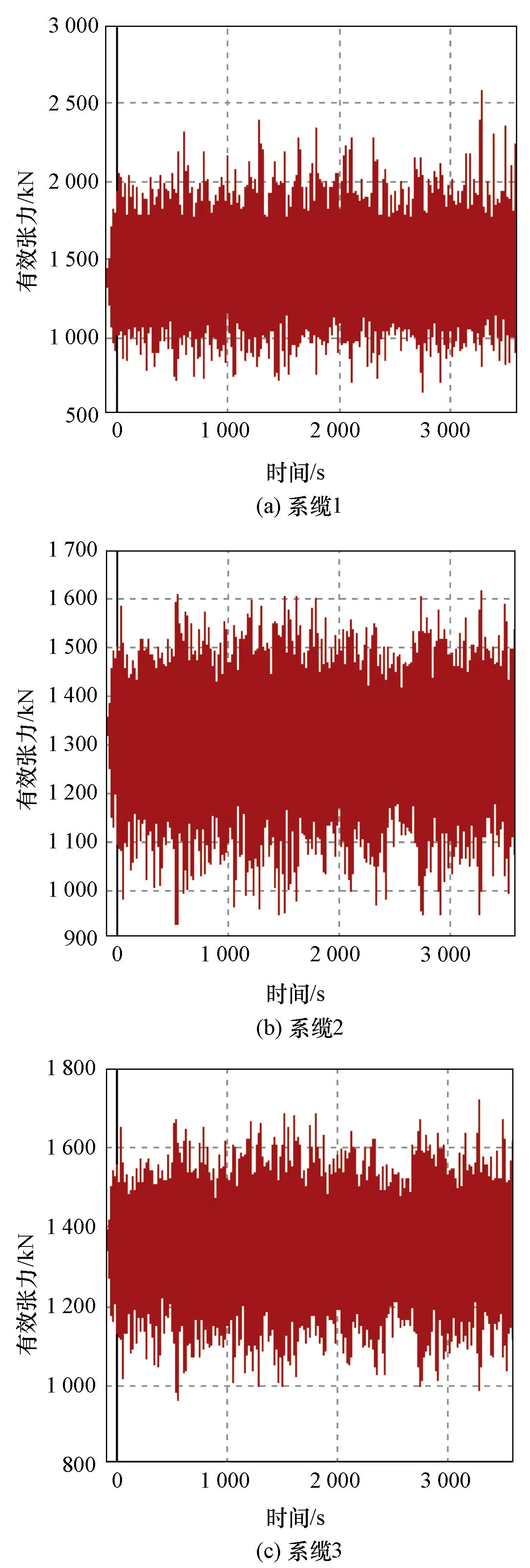
图6 3根系缆和顶端系缆端点A处的有效张力

随着时间的变化,端点A处的有效张力震荡变化。端点A处对系缆1的张力作用小于对顶端系缆的张力作用,且相差较大。顶端系缆的有效张力沿缆长变化不大,且曲率变化较小。顶端系缆上的平均有效张力大于任何一条分缆。

4 结语

在缆线曲率变化剧烈时,缆线的有效张力变化较大,当曲率降为0时会出现张力突变。相同曲率和相同缆长的缆线,在竖直方向投影大的有效张力较大,在水平方向投影大的有效张力较小。因此,在海水中铺缆时要尽量避免曲率突变,在曲率突然降为0时要注意对缆线的保护,并在此段选用张力突变性好的缆线。

在缆线端点处会不断发生有效张力的突变,但由于剪切力的最大值远小于有效张力,在计算缆线端点受力时只须考虑缆线张力。由于顶端缆线的张力较大,从经济角度考虑,顶端缆线与其他分缆可使用不同的材料,其中顶端缆线所用材料的强度应比分缆更高。