政府R&D 补贴分配策略探讨:创新“主力军”与“国家队”之争
2022-11-11郝一冰
赵 凯,郝一冰,王 健
(华侨大学数量经济研究院,福建厦门 361021)
1 研究背景
科技创新在中国特色社会主义现代化建设全局中处于核心地位。企业是我国科技创新体系中的“主力军”,他们面向市场需求并以实现利润最大化为目标,往往能在新产品开发、新技术应用等方面取得较多创新成果[1];而科研院所、高等院校等科研机构则是我国科技创新的“国家队”,承担着国家战略科研任务,他们关注科技领域的研究前沿并以实现社会福利最大化为目标,对于基础研究的理论突破和核心难题的技术攻关起到了举足轻重的作用[2]。国家“十四五”规划明确提出要坚持创新驱动发展,全面塑造发展新优势,集中力量解决我国当前面临的一系列“卡脖子”问题。这就要求进一步强化企业创新主体地位,形成以企业为主体、市场为导向、产研深度合作的科技创新体系。企业和科研机构在科技创新中优势互补,产研合作对于双方都是优化创新资源配置的合理选择[3]。然而,市场自发形成的产研合作机制中往往存在着企业创新动力不足、科研机构合作积极性不高等一系列问题,这就需要政府相关部门发挥制度环境的作用[4],通过R&D 补贴等普惠性干预手段来激励企业创新、引导和促进产研深度融合[5-7]。
学界关于政府R&D 补贴的理论分析多基于博弈论方法。Spencer 等[8]开创性地在多阶段博弈模型中引入了R&D 补贴因素,认为政府R&D 补贴可以促进企业的研发投入并改善企业利润。在此基础上,学者们进行了相关的拓展研究,发现如果没有政府R&D 补贴的介入,企业与科研机构皆不会主动进行共性技术研发[9],并且产研双方均无法实现帕累托最优[10]。这些研究论证了政府通过补贴干预产研合作及技术创新的必要性。Teirlinck 等[11]、卞元超等[12]以及徐建中等[13]均证实政府采取适当的补贴激励措施对企业和科研机构开展合作创新具有明显的驱动效果。马永红等[14]以及蒋兴华等[15]同样认为R&D 补贴作为一种激励策略,可有效改善企业和科研机构的研发收益。然而,以上研究大多聚焦企业在产研合作及创新过程中的动机与行为,而对科研机构的关注不足。另外,Blum 等[16]和Giebe 等[17]曾提出用类似拍卖机制的方式来解决固定预算补贴分配的问题,但由于科研机构与市场企业从事创新的目的存在差异:科研机构不进行生产和经营活动而仅从事研发创新工作,其科研经费、研发费用等完全由政府承担,因此目标与政府一致,皆为最大化社会总福利;而企业进行科研创新投入的目的则是最大化企业自身利润。因而拍卖机制对于科研机构来说是一种资源浪费。截至目前,有关政府R&D补贴分配策略的研究多集中在企业间的分配,并未涉及政府在科研机构与企业间应如何合理分配有限的R&D 补贴资源。
政府作为R&D 补贴政策的制定者和实施者,可用于支持创新的经费预算是有限的[18],应综合考虑资金的使用效率与成本、制定适当的补贴比率[19]。因此,在有限资源下,政府应如何优化创新“主力军”与创新“国家队”之间的创新资源配置?应如何改善R&D 补贴对科技创新的激励效果和利用效率?尤其是在面对不同的行业发展时,政府的R&D 补贴分配策略应当如何调整?这些都是政府在制定和实施R&D 补贴时面临的重要难题。为全面和深入地解答上述问题,本文通过构建涉及政府、企业和科研机构三部门的三阶段动态博弈模型,理论探寻政府补贴最优分配策略,探究行业规模、产研合作、技术溢出等一系列因素对政府R&D 补贴制定和实施的影响。
本文贡献主要在于:其一,从企业与科研机构的产研合作视角探寻政府R&D 补贴的最优分配策略,为理解R&D 补贴效能、优化实施政府R&D 补贴政策提供了一种新思路;其二,考察行业规模、企业与科研机构研发效率差异、市场技术溢出等因素对政府补贴分配策略的复合影响,为政府综合行业、市场、企业等层面信息,因势利导地制定R&D补贴政策提供理论依据。
2 理论分析
2.1 理论模型设计
假定创新系统中存在地方政府、科研机构与n家企业。政府为推动创新,以直接性R&D 补贴的形式向科研机构和市场企业提供创新支持。假设政府用于激励创新的R&D 补贴预算总额为1,θ表示政府为创新“主力军”(企业)提供的R&D 补贴额在预算总额中的比例,其具体形式如下公式(1)所示:

据此,可构建如下三阶段动态博弈模型:第一阶段,政府决定针对市场研发企业的R&D 补贴率s;第二阶段,研发企业决定其各自的研发投入水平xi,与此同时,受政府R&D 补贴支持的科研机构决定其研发投入水平;第三阶段,研发企业进行古诺竞争,并决定其各自的产量水平qi。
2.2 理论模型求解
采用逆向归纳法(backward induction)对动态博弈模型进行求解。第三阶段,企业进行古诺竞争。企业i的利润函数为:

反需求函数以及研发企业边际成本函数为:
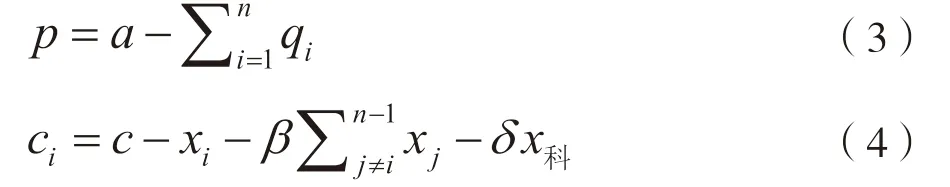
结合公式(2)、公式(3)与公式(4),企业i的利润函数可进一步整理为:

企业i通过决定产品产量qi来实现利润最大化。据此,对公式(5)求导,可得企业的一阶条件:
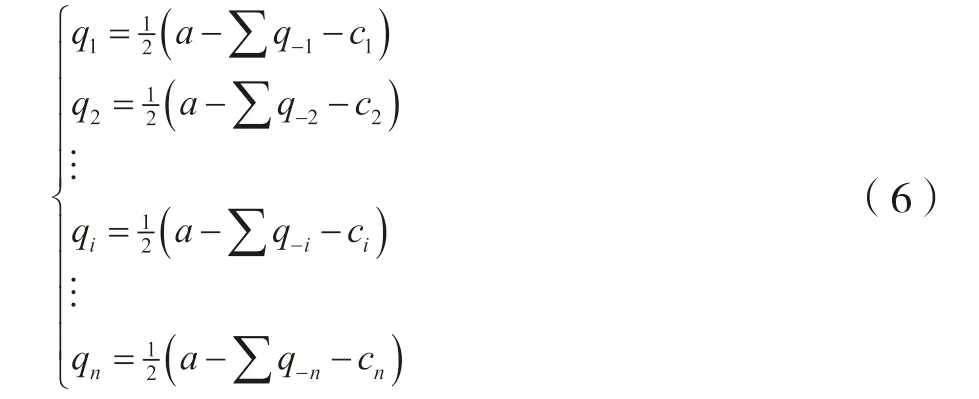
将上述n个方程加总整理后,可得总产量Q的表达式:
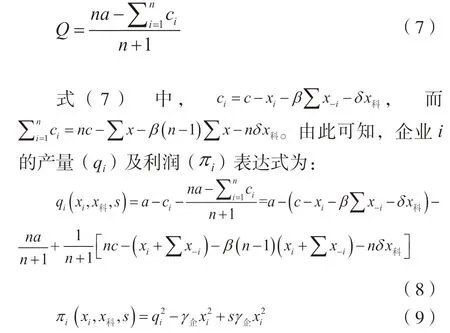
第二阶段,科研机构通过决定其研发投入水平来最大化社会福利,见公式(8),而市场企业则通过决定其研发投入水平 来最大化自身利益。


等式(12)的左侧为边际收益,右侧为边际成本,在均衡情况下,等式左侧将等于右侧。据此,可推导出科研机构研发投入 的反应函数,如公式(13):

由公式(11)与公式(13)可知,企业与科研机构的研发投入为互补策略。事实上,由于产研合作及溢出效应的存在,科研机构在研发上的投入可通过降低企业研发成本来激励企业加大研发投入。同样,企业研发投入水平的提升也能帮助科研机构更有效地最大化社会福利,进而提升其研发投入规模。将公式(11)与公式(13)联立,可计算出的表达式,如公式(14)、公式(15):


通过以上计算得到以下结论:
结论1:(1)只有当溢出效应达到或超过一定水平时,政府才会对企业实施R&D 补贴,并且该溢出效应门槛与企业所在行业的规模(即企业数量)具有一定的非线性关系。
(2)均衡情况下,政府向市场企业实施R&D补贴的强度仅与溢出效应和行业规模有关,而与产研合作程度无关。溢出效应越强,政府R&D 补贴强度越大。

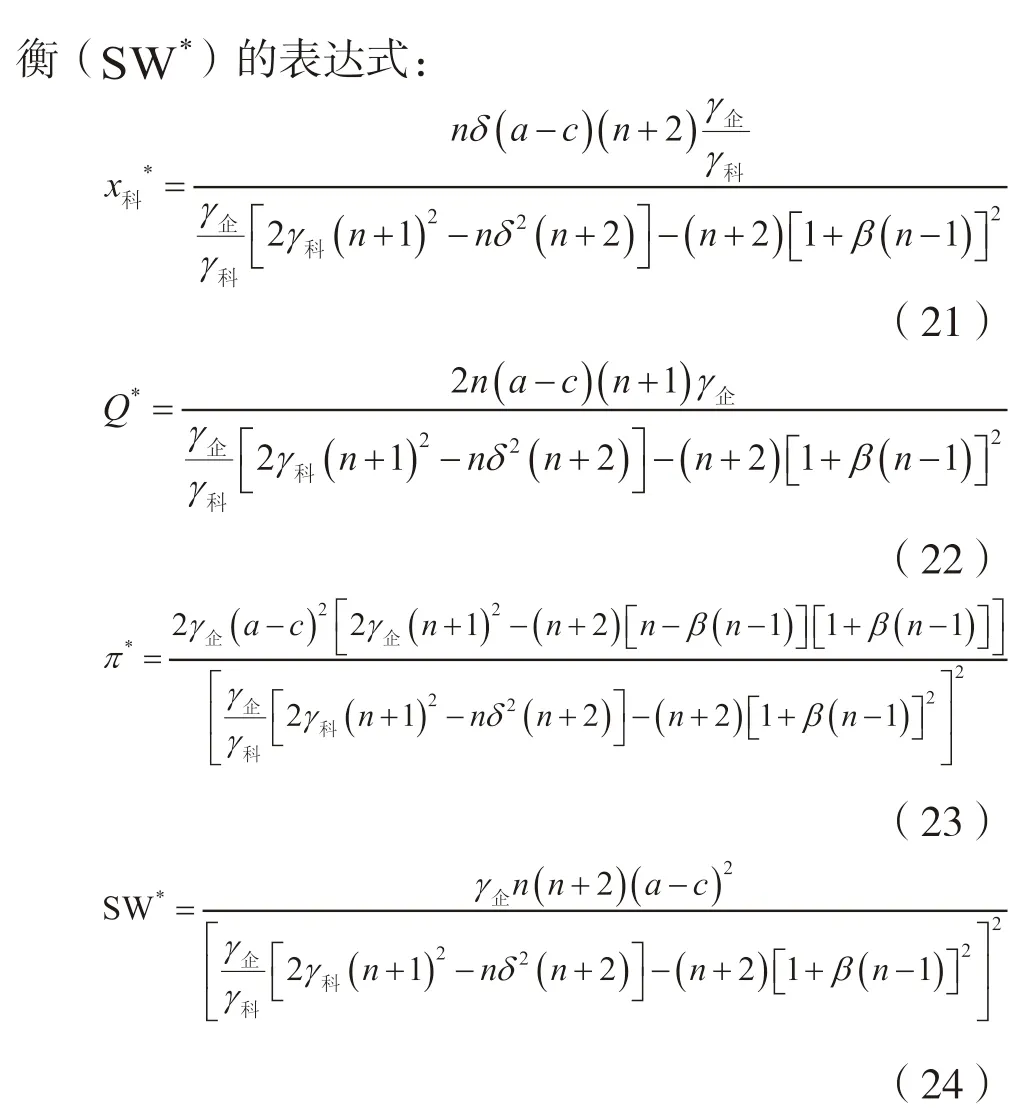
将企业研发投入均衡公式(20)和科研机构研发投入均衡公式(21)代入至公式(1),可得政府为创新“主力军”(市场企业)提供的补贴数额在预算总额中的均衡分配比例:

结论2:产研合作不仅有利于强化市场企业与科研机构的研发投入的意愿,还有益于企业利润、消费者福利以及社会福利水平的提升。
证明:对公式(20)~(25)求导,可得:
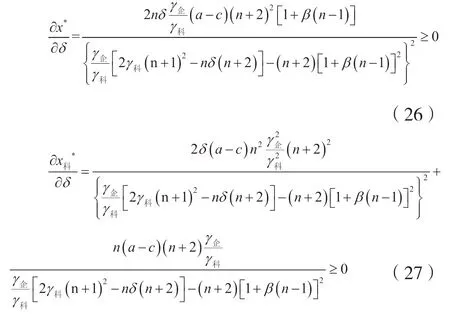

值得注意的是,政府R&D 补贴分配的实施方案往往会受到如企业研发效率、企业与科研机构的产研合作程度以及企业间溢出效应等因素的影响。借助公式(23)给出的政府R&D 补贴分配比例均衡的表达式,我们可得到如下结论。
结论3:(1)随着企业与科研机构的研发效率比值的增大,政府向科研机构投放的R&D 补贴资金比例也会相应提高。
(2)较高程度的产研合作会增强政府向科研机构实施R&D 补贴的意愿而降低政府对企业研发的支持力度。
(3)伴随溢出效应的增大,政府会提升补贴预算资金中向企业投放的比例。
证明:(1)求公式(25)关于企业和科研机构的研发效率比()的导数,可得:


行业内企业的知识和技术的溢出和共享有益于提升社会福利,这与政府利用补贴资金来推动创新以实现提高社会福利水平的目标一致。因而,伴随企业间溢出效应的增大,政府部门会提升补贴预算资金中向企业投放的比例。因此,企业要获得更多的R&D 补贴,应该加强彼此间的技术合作,设立产业技术同盟,这不仅有利于降低企业自身的生产及研发成本,更有利于社会整体福利水平的提高。
3 数值模拟
3.1 产研合作、行业规模与政府补贴分配比例
取0.25、0.5、0.75 分别代表“低”“中等”“高”三种不同水平的产研合作(),考察在不同产研合作程度下,政府补贴预算分配比例()与行业规模()间的关系,结果如图1 所示。
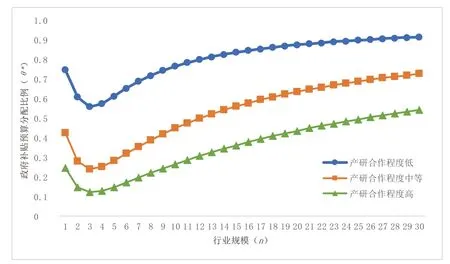
图1 产研合作、行业规模与政府补贴分配比例
由图1 可以看出,无论在何种产研合作程度下,政府补贴预算比例与行业规模之间均存在非线性关系:当时,随着行业内寡头企业数量的增加,政府更倾向于加强对研究机构的R&D 补贴力度;而当时,随着行业规模的扩张,政府会加大对企业研发的支持力度。此外,当行业规模一定时,低产研合作程度下的政府补贴预算分配比例最高,中等产研合作程度下的补贴预算分配比例次之,而高产研合作程度下的补贴预算分配比例最低。这说明较高程度的产研合作会增强政府向科研机构实施R&D 补贴的意愿,并降低政府对企业研发的支持力度。
当产研合作程度较低时,科研机构与市场企业合作研发的机会较少,科研机构较难通过企业将其研发成果产业化,难以起到提升和改善社会福利的作用,故政府会将大部分R&D 补贴分配给企业。而当产研合作程度处在中等或较高水平时,政府补贴预算分配比例往往会受到产研合作程度和行业规模的复合影响。具体来讲,行业规模较小时,产研合作对补贴预算分配比例的抑制作用占主导,政府会将大部分R&D 补贴分配给科研机构;而随着行业规模的扩张,规模效应逐渐显现,政府会逐渐将R&D补贴向市场中的研发企业倾斜。
3.2 技术溢出、行业规模与政府补贴分配比例
取0.15、0.3、0.6三个值分别代表“低”“中等”“高”三种不同水平的技术溢出效应(),考察在不同程度的溢出效应下,政府补贴预算分配比例()随着行业规模()增长的变化,结果如图2 所示。
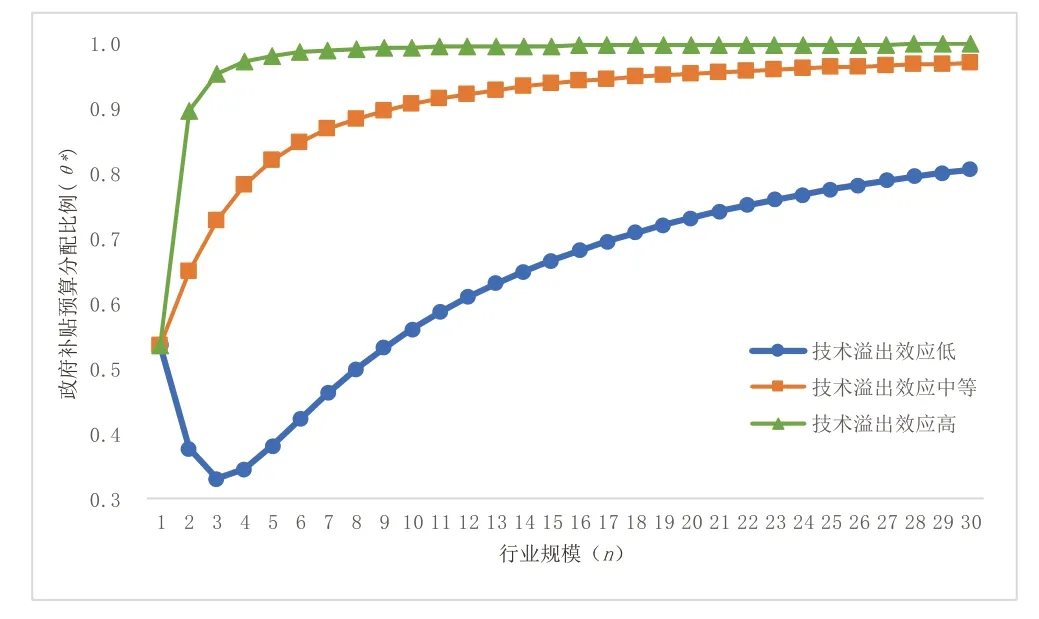
图2 技术溢出、行业规模与政府补贴分配比例
由图2 可知,在不同的技术溢出水平下,政府补贴预算分配比例会随着行业规模的扩大而显现出差异化的变化趋势。首先,当企业间技术溢出水平较低时,政府补贴预算分配比例与行业规模间呈“U”型关系。值得注意的是,当行业内部仅存在三家寡头企业时,政府补贴预算分配比例达到最小。此时,政府会将大部分补贴用于支持科研机构的研发活动。而伴随行业规模的不断扩大,政府R&D 补贴的实施目标会逐步转向市场企业。其次,当企业间的技术溢出处于中等或较高水平时,政府补贴预算分配比例与行业规模呈正相关关系,并且行业规模对补贴预算分配比例增长的边际效益是递减的。除此之外,当行业规模一定时,较高溢出效应水平下的政府补贴预算分配比例往往较大,而在较低技术溢出水平下,政府给市场企业分配的R&D 补贴比例较小。
3.3 研发效率比、行业规模与政府补贴分配比例
取0.5、1、1.5 三个值分别代表“低”“中等”“高”三类不同水平的企业与科研机构研发效率比(),考察在“企业-科研机构”研发效率比存在差异的情况下,政府补贴分配比例()与行业规模()的关系,结果如图3 所示。中等的研发效率比意味着企业和科研机构研发效率相同,而较低(较高)的研发效率比则意味着企业(科研机构)研发效率相对更高。由图3 可知,在不同水平的企业与科研机构研发效率比下,政府补贴预算比例与行业规模均存在非线性关系。政府在实施R&D 补贴时,往往会比较产研合作双方的研发效率,并将补贴预算分配比例向更高研发效率的一方倾斜。
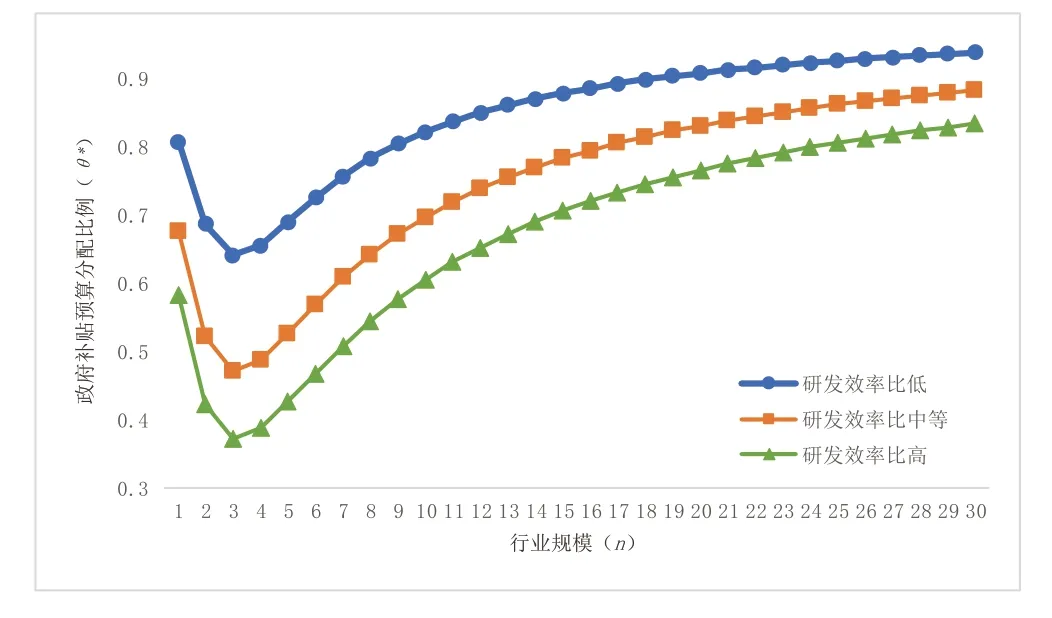
图3 研发效率比、行业规模与政府补贴分配比例
4 结论
本文针对如何将政府有限的补贴资金在“创新主力军”(企业)与“创新国家队”(科研机构)之间进行“最优”分配这一重要问题进行解答。本文通过构建涉及政府、企业与科研机构三部门的三阶段动态博弈模型,理论探寻政府补贴最优分配策略,探究行业规模、产研合作、技术溢出等一系列因素对政府R&D 补贴制定和实施的影响。研究证实:(1)只有当溢出效应达到或超过一定水平时,政府才会对企业实施R&D 补贴,并且伴随溢出效应的增大,政府会提升补贴预算资金中向企业投放的比例;(2)政府向市场企业实施R&D 补贴的强度仅与溢出效应和行业规模有关,而与产研合作程度无关,溢出效应越强,政府R&D 补贴强度越大;(3)产研合作不仅有利于强化市场企业与科研机构的研发投入的意愿,还有益于企业利润、消费者福利以及社会福利水平的提升,较高程度的产研合作会增强政府向科研机构实施R&D 补贴的意愿而降低政府对企业研发的支持力度。
本文仍存在以下不足:其一,考虑到政府对不同类型企业(如,行业龙头企业、小微企业等)可能会采取不同的策略,因而有必要在未来研究中将企业异质性纳入分析框架;其二,因市场企业间的溢出效应可能是内生引起的,未来可在溢出效应内生的情况下,进一步考察产研合作与技术溢出能否影响政府补贴预算分配比例。
