LLC谐振变换器控制策略研究

王暄

（青岛西海岸新区中德应用技术学校 山东省青岛市 266400）

近年来，随着科学技术的飞速发展，PWM变换器已经广泛应用于电工电子、航天、医药、通信等领域，对于常见的DC-DC和AC-DC电路，控制方式比较单一，只能通过控制移相角来调节输出电压，如果改变频率，体积会相应的减小，但是损耗却是成倍的增加，效果非常差。在这种背景下，LLC谐振变换器就出现了。相比于其他的DC-DC电路，LLC谐振变换器不仅可以通过改变MOS管开通和关断的频率调节输出电压，开关频率高了，功率密度也高了，整体的结构也变小了，最关键的是可以实现MOS管的零电压开通和二极管的零电流关断，减小了MOS管的损耗，整体效率就相应的提高了。

本文采用三电平半桥LLC谐振变换器为研究对象，结构如图1所示。一般有两种调制策略：变频调制策略和移相调制策略。本文根据现有控制策略的弊端，研究了一种混合式调制策略[2]，通过软开关的边缘点自由切换改变开关频率和改变移相角两种模式，使输出电压的调节幅度最大，并对该谐振变换器混合式策略的电压增益、软开关和电压调节幅度等特性进行了详细的研究分析。

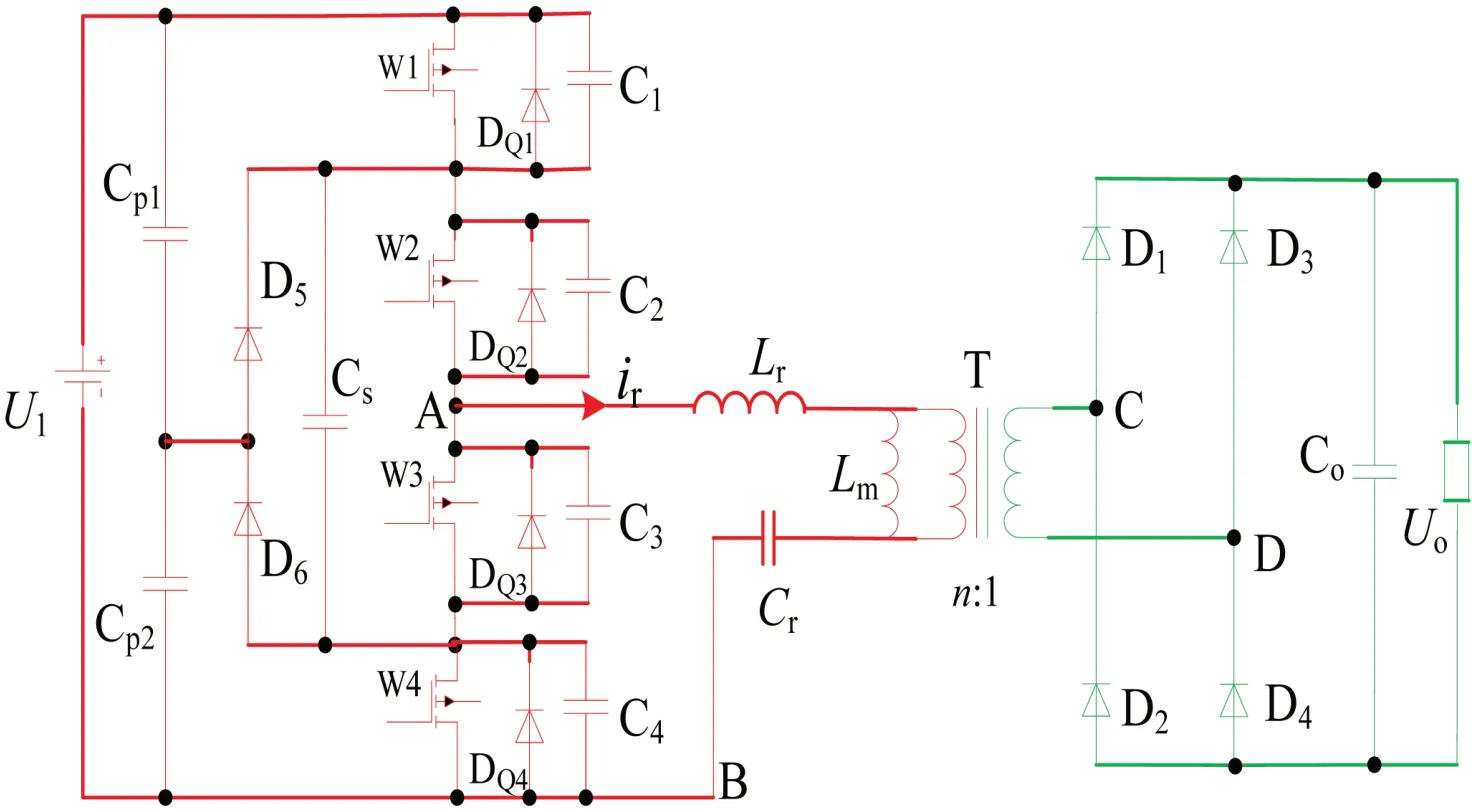
图1：三电平半桥LLC谐振变换器

1 混合式调制策略

文献[2]详细陈述了混合式调制策略的实现过程，其基本控制思想如图2所示。

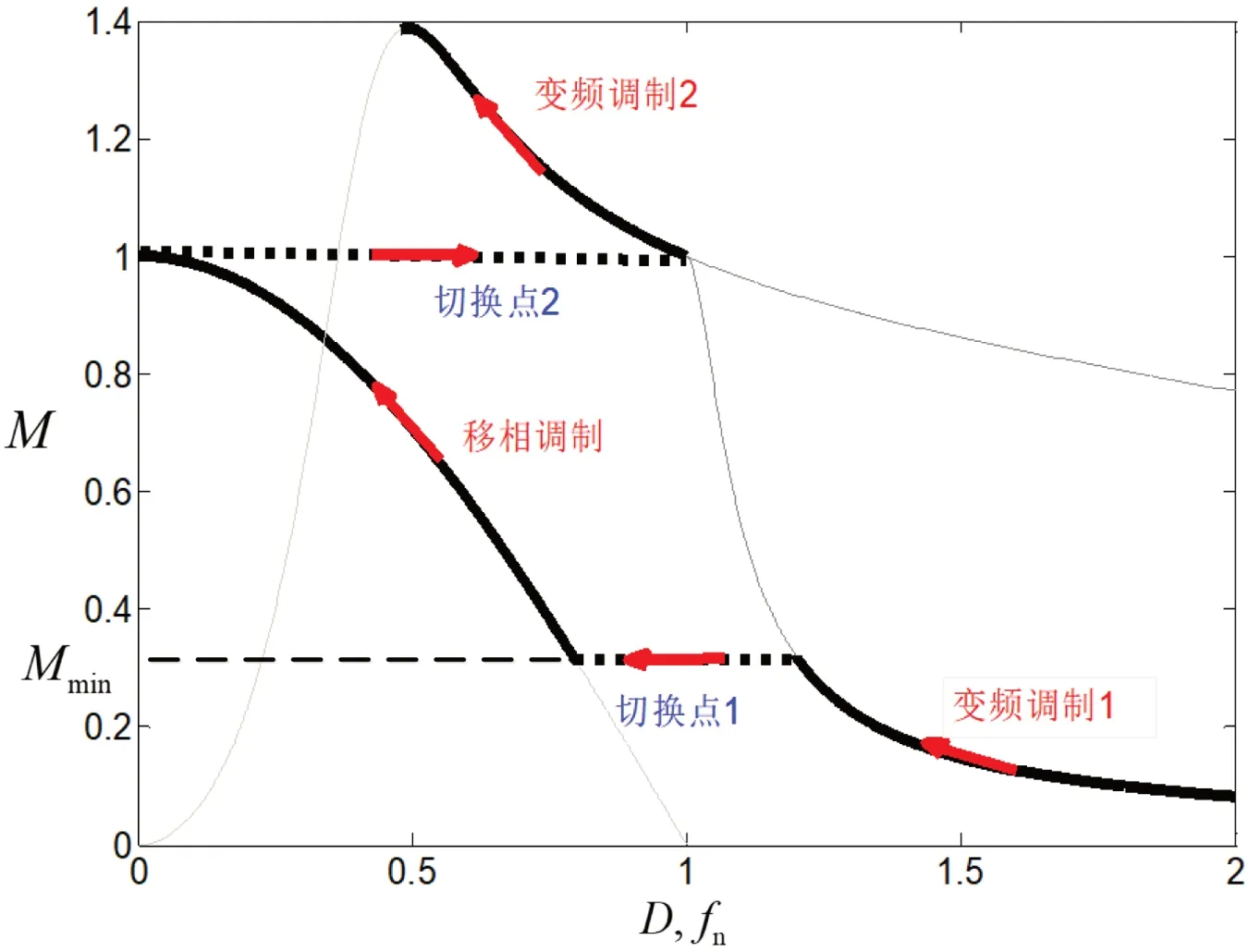
图2：混合式调制策略

其中，Mmin是根据移相调制模式下软开关的临界值求出的最小的电压增益。以Mmin为边界，电压增益低于Mmin的部分范围用改变开关频率调制模式，电压增益在（Mmin，1）的范围用改变移相角调制模式，电压增益在（1，Mmax）的范围用改变开关频率调制模式。两个切换点分别为Mmin点和1点。黑色实线描述的就是整个调制策略的控制过程。

2 工作过程

变换器在混合式调制策略下的相关曲线如图3所示。图中，U1～U4分别表示开关管W1～W4的开通与关断信号，W1与W4以及W2与W3的开通与关断正好相差180°,W2与W1的开通与关断角度产生了相位差，该相位差用移相比D来表示，其中（D'=1-D），有0≤D≤1。开关频率fs不是一个不变的值，移相比D和开关频率fs可以同时变化，同时调节D和fs使得输出电压的范围更宽。这与之前见过的只调节一个变量的控制策略相比，有了更多的可能性。

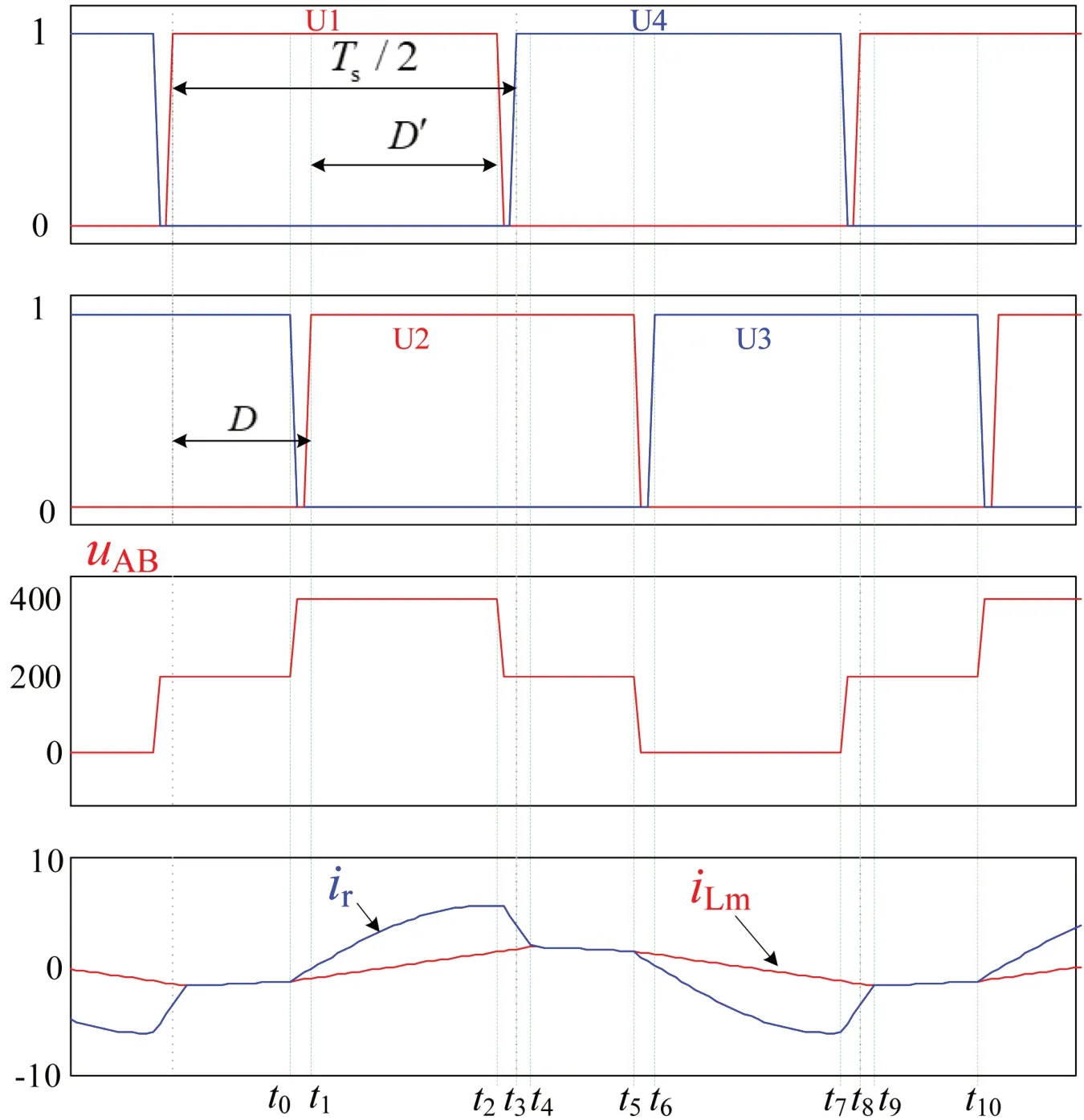
图3：变换器的工作波形

变换器在半个周期内分为6个过程，各个过程的工作原理都和移相调制的工作过程类似，只不过这里的开关频率fs是一个变化的值。

过程1[t0-t1]：

在t0时间点之前，场效应管W1和W3导通，场效应管W2和W4关断。在t0时间点，场效应管W3关断，流过谐振环的电流小于0，在电流的作用下，场效应管W3两端电容通过电容Cs充电，MOS管W2两端电容通过电容Cs放电。谐振电感和谐振电容共同工作在谐振状态，励磁电感Lm在-nUo的作用下线性下降。到t1时间点，场效应管W3两端电压为U1/2，场效应管W2两端电压为0。

过程2[t1-t2]：

在t1时间点，场效应管W2 两端电压变为0，所以W2可以实现电压软开关，流过谐振环电流的方向改变。励磁电感Lm两端电压为nUo，流过励磁电感的电流正向迅速升高，(Ui-nUo)给谐振环供电，谐振电感和谐振电容共同工作在谐振状态。

过程3[t2-t3]：

在t2时间点，场效应管W1关断，流过谐振环的电流大于0，在这一过程，场效应管W1两端电容充电，场效应管W4两端电容放电。谐振电感和谐振电容处于谐振状态，流过励磁电感的电流正向迅速升高。到t3时间点，场效应管W1两端电压为输入电压的一半，场效应管W4 两端电压变为0，二极管DQ4导通，为W4的电压软开关做好准备。

过程4[t3-t4]：

在t3时间点，场效应管W4开通，场效应管W1两端电容充电至输入电压的一半，D5导通，这时流过谐振环的电流大于流过励磁电感的电流，电容C5通过W2和DQ4给谐振环供电。谐振电感和谐振电容共同工作在谐振状态，流过励磁电感的电流继续迅速升高，流过谐振环的电流下降，直到iLm=ir。

过程5[t4-t5]：

在t4时间点，流过谐振环的电流等于流过励磁电感的电流，变压器副边整流二极管截止，和变压器原边彻底分开，励磁电感加入进来和谐振电感、谐振电容共同工作在谐振状态，当前的谐振频率变为由于励磁电感本身的数值较大，谐振周期也同样很大，电流在这一过程中基本保持不变，变压器副边大电容Co给负载供电。

过程6[t5-t6]：

在t5时间点，场效应管W2关断，在这一过程内，流过谐振环的电流流经电容Cs给W2两端电容充电，给W3两端电容放电，场效应管W2 两端电压Uc2急速升高，场效应管W3 两端电压Uc3急速下降，当Uc3减小到0时，场效应管W3导通，从而实现电压软开关。

3 特性分析

3.1 电压增益

大量文献表明基波近似法（first harmonic approximation,FHA）[11]是分析电压增益的有效方法。但是这种方法只适用于开关频率fs是恒定的值的条件下，如果开关频率是一直变化的，就不能用基波近似法来分析了。对于混合式调制来说，简单的等效电路分析已经不适用了，只能将整个变换器电路分解，分成三个部分，即三电平半桥逆变电路（DC-AC），谐振环电路，二极管全桥整流电路。这三部分电路相互独立，但又通过输入输出电压紧密的联系起来，如图4所示。

图4：LLC谐振变换器分解图

电压增益为：

3.1.1 三电平半桥逆变电路：

文献[2]移相调制模式特性分析中，谐振环的输入电压uAB为：

将uAB进行傅里叶变换，得到基波为：

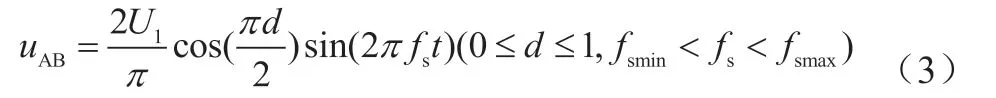
电压增益为：

3.1.2 谐振环电路

谐振环的等效电路如图5所示。

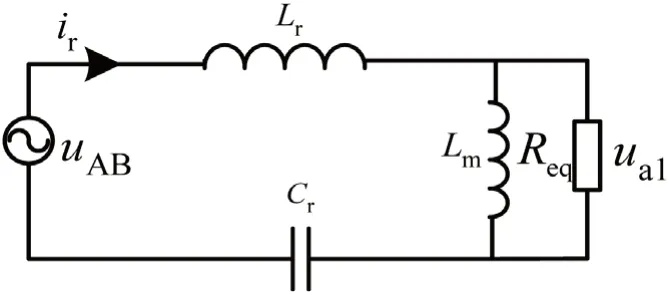
图5：谐振腔等效电路

由图5的等效电路可以得到谐振环的输入阻抗为：

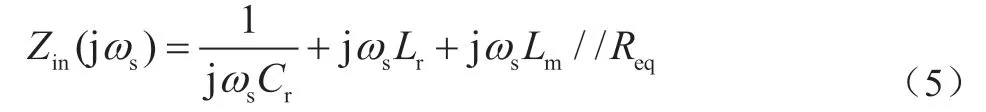
谐振环的电压增益为：

3.1.3 二极管全桥整流电路

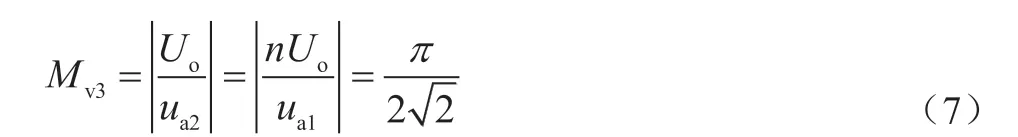
所以，LLC谐振变换器电压增益为：

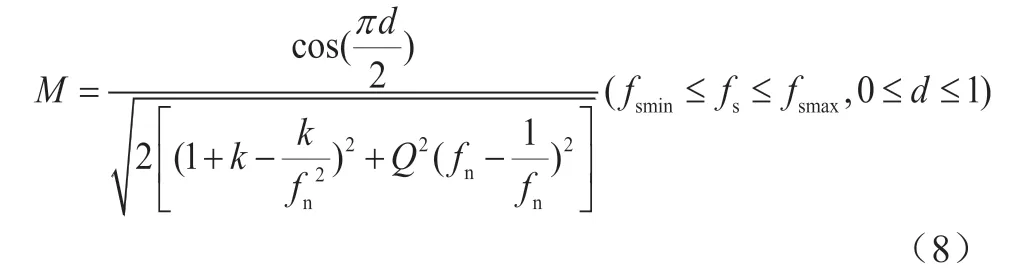
从式（8）可以看出，当移相比d=0时，电压增益的表达式和变频调制完全一样，当公式里面的fs等于谐振频率fr时，电压增益的表达式则和移相调制完全一样。从式（8）可以看出，混合式调制策略同时改变移相比d和开关频率fs，也可以改变电压的增益。

图6描述了轻载时（Q=0.4），移相比和开关频率同时变化时的曲线。从图中可以看出，随着fn从0.8增大到2，其电压增益变小了，开关频率越大，电压增益反而变小了。随着d的增大，电压增益也慢慢的变小了。同时改变两个参数，可以使电压增益发生变化。

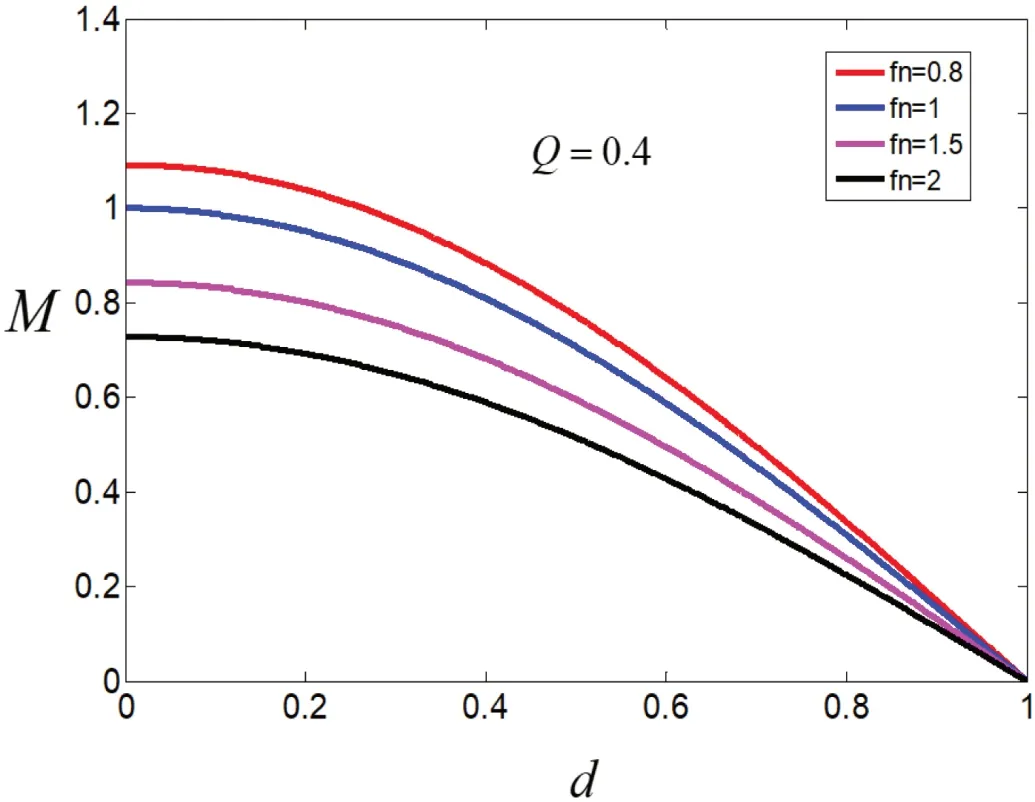
图6：不同频率（fn）下d与M的电压增益曲线

图7描述了移相比d=0.3时，改变负载的条件下，开关频率和电压增益的关系图。在此模式下，移相角为定值，这是单纯的变频调制。该曲线和变频调制的曲线非常接近，从图中可以，看出轻载时（Q越小）开关频率高于谐振频率这一段区域内电压增益基本保持不变，改变开关频率，基本对电压增益没什么影响。

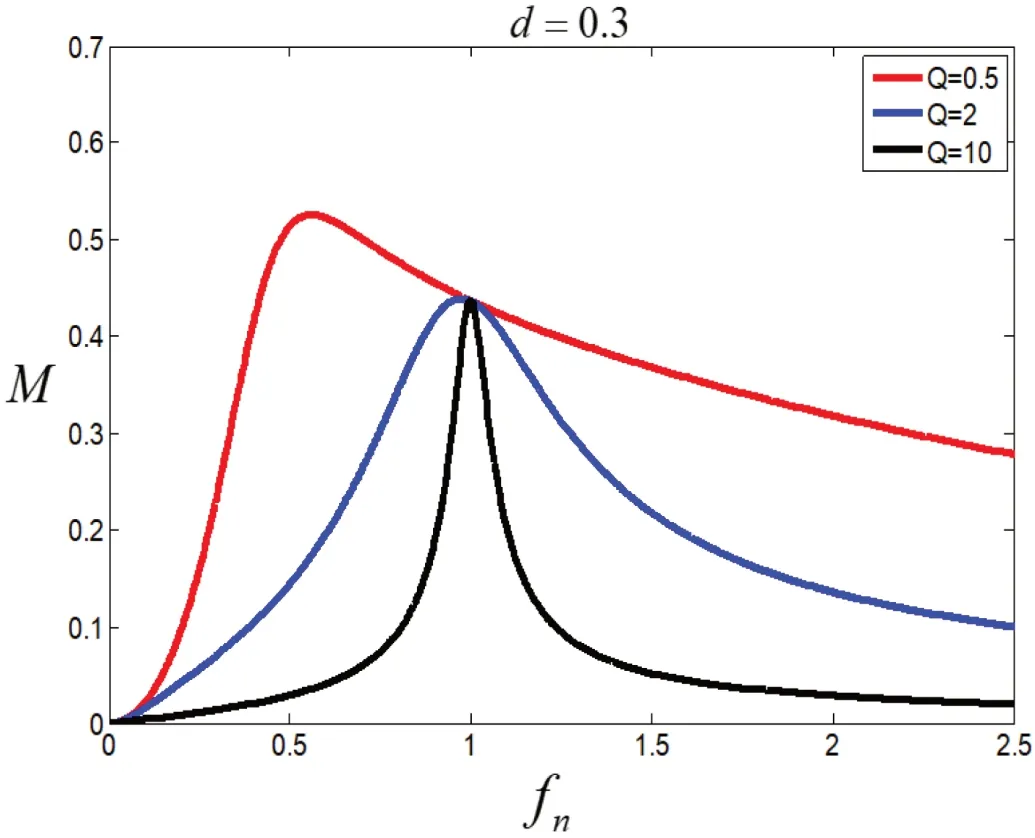
图7：不同负载（Q）下fn与M的关系曲线

3.2 软开关分析

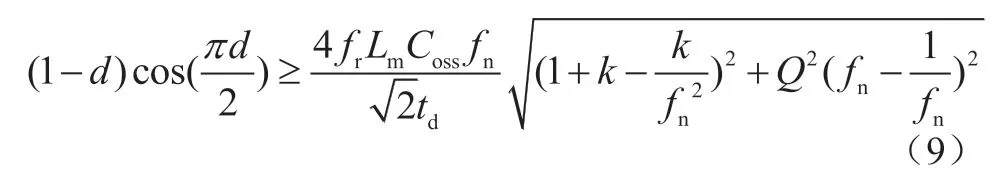
当负载变化，k=0.4时移相角和开关频率的关系曲线如图8所示。

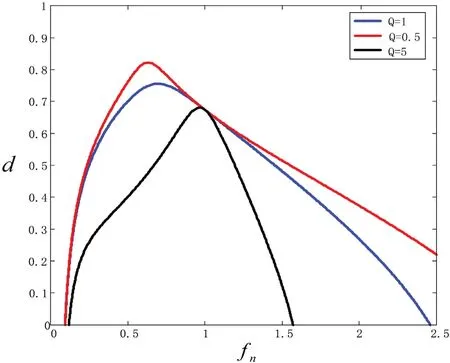
图8：移相角和开关频率fs的关系曲线

从图8中可以看到，当fn取一定值f0时，移相比d可以取到最大值dmax，但是dmax的值与负载的大小相关，当fn＞f0时，这一段范围开关频率要大于谐振频率，开关频率上升，移相比d则下降。而fn＜f0时，这一段范围开关频率要小于谐振频率，开关频率的下降，移相比d也下降。而且负载越大，开关频率变化范围却越来越小。所以，混合式调制策略在改变移相比d和开关频率fs的时候，要注意软开关的临界范围，不能超出软开关的临界范围，否则效率就会降低。

3.3 电压调节范围

从前两个特性分析可知，负载不变时，开关频率的最小值fsmin和开关频率的最大值fsmax也是不变的，是两个定值。在fsmin≤fs≤fsmax，0≤d≤1范围内，电压的调节幅度是由移相比d和开关频率fs共同决定的。

由式（8）可以得出负载Q=0.4时电压增益M与移相比d，开关频率fs的关系如图9所示。

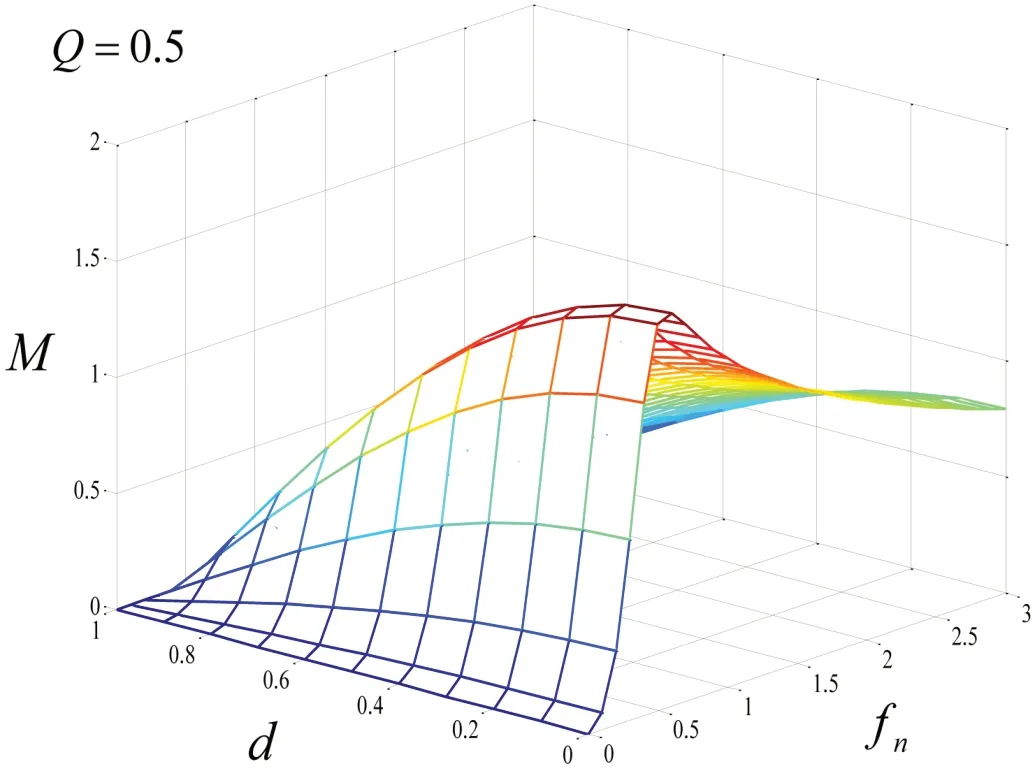
图9：电压增益M与移相角，开关频率fs的关系曲线

结合式（9），可得：

由式（10）可以推导出该变换器的电压调节范围。

3.3.1 找最小值Mmin点

根据拉格朗日乘数法可得到下式：

3.3.2 找最大值Mmax点

从式（11）可以看出，当没有移相时，电压增益有最大值Mmax，这意味着此时没有移相调制，只有变频调制。但是负载不同时，其电压增益的最大值Mmax点也改变了。当fs=fs0时，有最大值Mmax点：

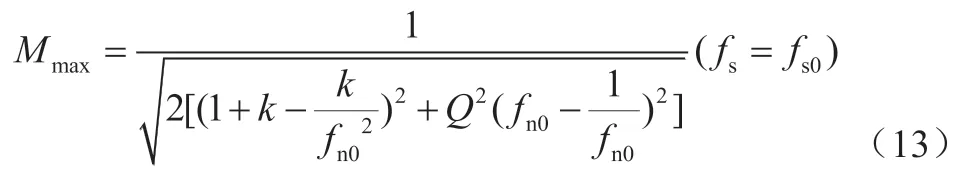
那么输出电压可调的范围为(Mmin,Mmax)，其电压调节范围如图10所示。

图10：Q=0.5时电压增益和软开关曲线

4 总结

为了解决输出电压幅度宽的控制，本文根据现有的调制策略的弊端，提出了一种混合式调制策略，在该调制策略下可以实现输出电压的调节幅度更广。并对该混合式控制策略的特性从三方面进行了研究：电压增益特性、开关管软开关特性和电压调节范围特性，分析了实现软开关的影响因子和条件，推导出了LLC谐振变换器了实现软开关的公示和影响因子，并对变换器的电压增益进行了分析，并找出该策略下输出电压的最大调节幅度。