混合梁斜拉桥边中跨比布置对受力特性影响探究

2022-11-11李大勇

中国公路 2022年16期

李大勇

（中交通力建设股份有限公司，陕西西安 710075）

边中跨比是斜拉桥总体布置的重要参数，对结构刚度及各构件受力都有重要影响。斜拉桥索塔在恒载作用下的弯矩接近于零，主梁在恒载作用下的弯矩接近于刚性支承连续梁的弯矩,这是斜拉桥理想的恒载状态[1]。混合梁斜拉桥要达到这一理想恒载状态，需要合理的边中跨比例，使得索塔两侧的主梁处于重量平衡状态[2]。在混合梁斜拉桥中，边跨混凝土梁具有锚固及配重的作用，混凝土边跨和密边跨提供的稳固支撑还能减小拉索的疲劳效应[3]。因此，斜拉桥合理的边中跨比例是使索塔和主梁处于较理想恒载状态的关键因素[3]。

本文以某大跨度混合梁斜拉桥为研究背景，参考规范选取不同的边中跨比。从理想恒载状态出发，基于空间有限元方法，分析桥梁结构的主梁应力、主塔受力、斜拉索索力及动力特性等力学性能，由此得出混合梁斜拉桥的最优边中跨比。

一、工程背景及有限元分析模型

（一）工程背景

某大桥为双塔双索面混合梁斜拉桥结构，跨径布置为150m+400m+150m，双向四车道建设。主塔采用H形桥塔，主塔塔身设置上中下三道等截面横梁；辅助墩及过渡墩采用双柱式墩。中跨采用双边“上”字形钢主梁结合桥面板的整体断面，边跨主梁采用混凝土边主梁形式。

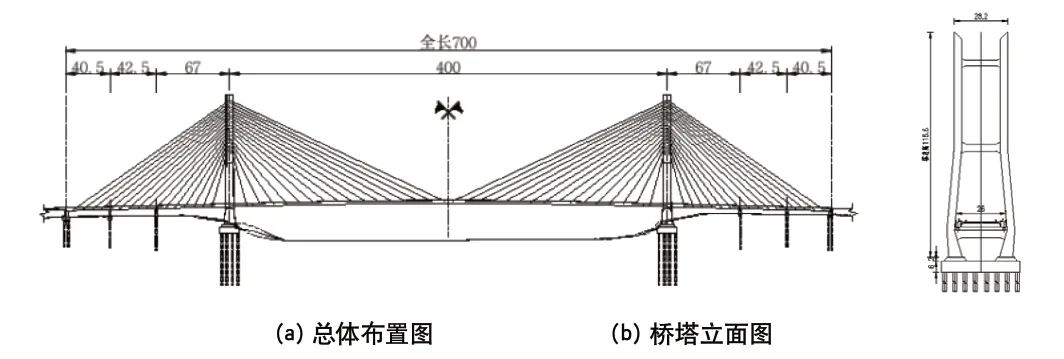
图1 某斜拉桥布置图

（二）有限元分析模型

全桥静动力分析采用迈达斯（Midas）有限元程序，共有908个节点、1386个单元，全桥有限元模型如图2所示。其中主塔和主梁采用梁单元，斜拉索采用桁架单元，塔墩底约束采用一般支撑约束模拟。该桥属于对称结构，分析时仅建立一半桥梁模型。定义荷载组合为“自重+二期恒载+车辆荷载+整体升温5度”。

图2 空间杆系有限元模型

二、边中跨比例选取

《公路斜拉桥设计规范》（JTG/T 3365-01—2020）中规定部分设计参数为区间形式，例如双塔斜拉桥的边中跨比宜为0.3～0.5，双塔及多塔斜拉桥桥面以上塔高与主跨的跨径比宜为1/3～1/6[4]。

结合背景工程特点，不改变原桥跨度，改变桥墩位置以改变边中跨比，选取了边中跨比为0.35、0.375、0.4三种体系。基于有限元分析方法，分析研究三种不同边中跨比桥梁的力学性能。

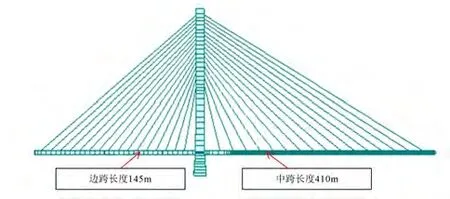
图3 边中跨比0.35桥梁

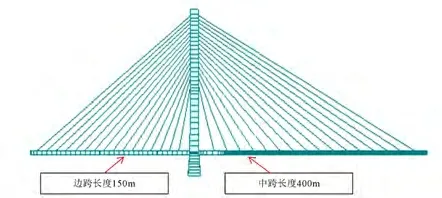
图4 边中跨比0.375桥梁

图5 边中跨比0.4桥梁

三、边中跨比例对受力特性影响

（一）主梁应力

三种不同边中跨比的混合梁斜拉桥对主梁应力的影响，如图6所示，边中跨比为0.35的混合梁斜拉桥，主梁应力最大值为13.7MPa；边中跨比为0.375的混合梁斜拉桥，主梁应力最大值为12.8MPa；边中跨比为0.4的混合梁斜拉桥，主梁应力最大值为13.3MPa。在桥塔处主梁应力会增大，且主梁下缘应力大于上缘应力，所以选取主塔处主梁下缘应力作为研究对象。如图7所示，边中跨比0.375时主梁应力最大值最小，反之，边中跨比0.35时主梁应力最大。

图6 不同边中跨比主梁上下缘应力对比

（二）塔顶位移

三种不同边中跨比的混合梁斜拉桥对塔顶位移的影响如图8所示，边中跨比0.35时塔顶位移最大，比边中跨比0.375时大36.8%；边中跨比0.4时塔顶位移最小，比边中跨比0.375时小5.3%。

图7 不同边中跨比桥塔处主梁下缘应力对比

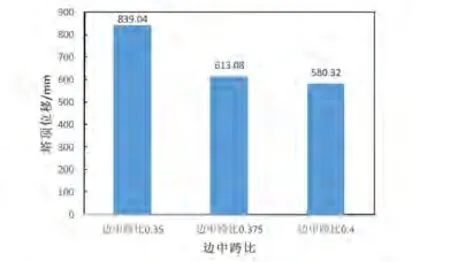
图8 不同边中跨比塔顶位移对比

（三）塔底弯矩

三种不同边中跨比的混合梁斜拉桥对塔底弯矩的影响，如图9所示，边中跨比0.35时塔底弯矩为939006.1kN·m，边中跨比0.375时塔底弯矩为700292.9kN·m，边中跨比0.4时塔底弯矩为678763.1kN·m。边中跨比0.35时塔底弯矩最大，比边中跨比0.375时大34.1%；边中跨比0.4时塔底弯矩最小，比边中跨比0.375时小3.1%。

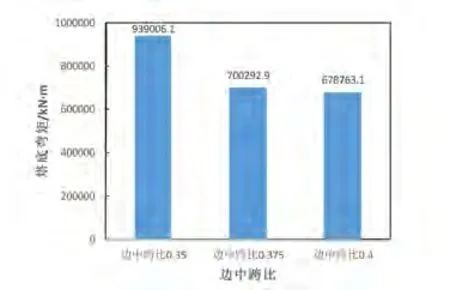
图9 不同边中跨比塔底弯矩对比

（四）斜拉索索力

三种不同边中跨比的混合梁斜拉桥对拉索索力的影响如图10所示，边中跨比0.35时拉索索力最大值为8002.4kN，边中跨比0.375时拉索索力为7836.5kN，边中跨比0.4时拉索索力为8225.4kN。边中跨比0.375时拉索索力总体最小且较为平稳，边中跨比0.4时拉索索力最大且总体变化较大，边中跨比0.35时拉索索力也较大且处于不太合理的状态，可得拉索索力在中跨第一根拉索处于结构的最大索力。如图11所示，边中跨比0.375时中跨第一根索处索力最小，边中跨比0.4时最大，边中跨比0.375时拉索索力最为合理。

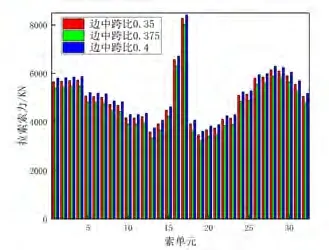
图10 不同边中跨比中跨拉索索力对比

图11 不同边中跨比中跨1号拉索索力对比

（五）动力特性

动力荷载作用下桥梁结构振动增大，可能引起结构局部疲劳损伤，会形成影响桥上行车舒适和安全的振动变形和加速度，甚至使桥梁完全破坏[5]。除车辆荷载外，桥梁结构主要承受的动力荷载包括风荷载及地震荷载[5]。本文采用子空间法计算分析混合梁斜拉桥模型的自振特性，三种结构体系前3阶自振频率和振型对比如表1所示。

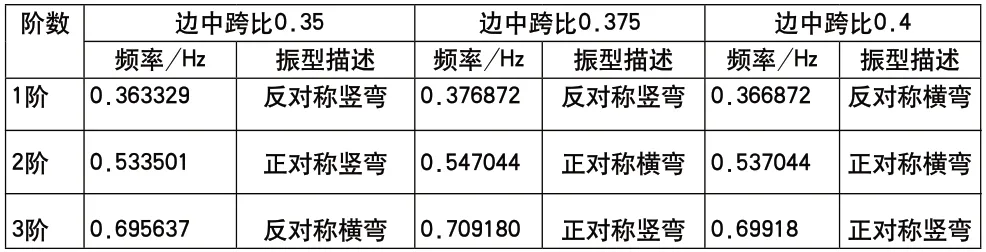
表1 不同边中跨比的自振模态对比

如表1所示，3种不同边中跨比桥梁前3阶振型均为竖弯与横弯；3种不同边中跨比模型前3阶振型特性基本一致，边中跨比0.375的各阶横弯和竖弯频率与其它两个位置相比均有所增加，边中跨比0.375的自振频率明显高于另外两处位置，整体基频增加4%左右。3种不同边中跨比的动力特性都符合规范要求。

四、边中跨比例对比分析

不同边中跨比结构的静动力有较大不同。对于主梁应力，边中跨比0.35比边中跨比0.375大7.0%，边中跨比0.4比边中跨比0.375大3.9%。对于塔顶位移，边中跨比0.35时塔顶位移最大，边中跨比0.4时塔顶位移最小，但边中跨比0.375时塔顶位移只比边中跨比0.4大33mm。边中跨比0.4时塔底弯矩最小，边中跨比0.35时塔底弯矩最大，边中跨比0.375时塔底弯矩远小于边中跨比0.35，比边中跨比0.4稍大。边中跨比0.375时中跨第一根索处索力最小，边中跨比0.4最大，边中跨比0.375时拉索索力最为合理，故对于拉索索力边中跨比0.375为最佳比例。对于动力特性，边中跨比0.375的前7阶特征值比边中跨比0.35高，边中跨比0.35比边中跨比0.4高，同时边中跨比0.375时振型变化最小，为最合理的边中跨比。综合不同边中跨比对桥梁的静动力影响分析，得出边中跨比0.375具有较大优势。