双重部分函数型回归模型的贝叶斯估计
2022-11-10徐登可田瑞琴吴刘仓
徐登可 ,田瑞琴,吴刘仓
(1.杭州电子科技大学 经济学院, 浙江 杭州 310018; 2.杭州师范大学 数学学院, 浙江 杭州 311121; 3.昆明理工大学 理学院, 云南 昆明 650093)
0 引言
在现如今大数据时代,随着电子信息技术的快速发展和先进测量工具的出现,大量数据可以廉价地被收集和存储.其中在金融工程、环境科学、医学、脑成像、公共卫生等应用领域,常常会获得带有明显函数特性的数据,即观测数据是在空间或时间上的一个或多个维度上获得的,这一类型的数据称之为函数型数据.近年来,函数型数据分析已经成为越来越热的统计研究方向,且受到了很多统计学家的关注.例如,Ramsay和Dalzell[1]详细介绍了具有函数型协变量和标量响应变量的函数型线性回归模型.Shin[2]提出了部分函数型线性回归模型,并研究了模型中未知回归系数的理论性质.Lu等[3]研究了分位数部分函数型线性回归模型,且获得了模型中未知参数和函数型系数的渐近理论性质.Yu等[4]研究了变系数部分函数型线性分位数回归模型.Zhou和Peng[5]研究了缺失数据下部分函数型线性回归模型的参数估计. Yu等[6]提出了单指标部分函数型线性回归模型.其他的函数型回归模型研究还可以参见文献[7-9].不难发现,上述函数型数据分析文献主要基于模型方差齐性的假设,即模型误差的方差是相等的.众所周知,模型或者数据存在异方差时,采用现有的大多数统计推断方法都有可能导致错误的推断.
然而,目前处理异方差数据最常用的方法是方差建模法,即不仅对均值建立回归模型,同时也对方差建立回归模型进行分析,有些文献称之为双重回归模型或者联合均值与方差模型.这个模型主要体现了对方差的重视,它能更好地解释数据变化的原因和规律.特别最近这些年已经有很多学者对基于方差建模的异方差模型研究了模型的参数估计、变量选择以及异方差检验等统计推断.例如,吴刘仓等[10]对联合均值与方差模型提出一种同时对均值模型和方差模型的变量选择方法;赵远英等[11]对响应变量带有不可忽略缺失数据的联合均值与方差模型的贝叶斯估计问题进行了研究;戴琳等[12]基于联合均值与方差模型研究了模型的参数估计与基于数据删除模型考虑了统计诊断问题.其他类似的相关研究还可以具体参见文献[13-15].发现这些文献大多数都是基于非函数型异方差模型展开统计分析的,很少有文献和学者基于方差建模研究异方差函数型数据回归模型的贝叶斯参数估计等统计推断问题.
因此,本文主要基于方差建模针对异方差函数型数据提出了双重部分函数型回归模型,应用Gibbs抽样和Metropolis-Hastings算法相结合的混合MCMC算法研究模型的贝叶斯估计.
1 模型与似然函数
1.1 双重部分函数型回归模型
考虑经典部分函数型回归模型如下:
(1)
其中:Yi表示第i个个体的实值响应变量,Zi表示p维标量型解释变量向量,Xi(t)∈L2(T)是函数型解释变量,L2(T)表示定义在概率空间上均值为零,二阶矩有限的随机过程,并且不失一般性假设T=[0,1];θ=(θ1,θ2,…,θp)T是未知p维回归参数,β(t)是定义在[0,1]上的平方可积函数;εi是独立同分布服从于均值为零,方差为σ2的正态分布,即εi~N(0,σ2).
为方便描述,使用矩阵形式表示模型(1).令Y=(Y1,Y2,…,Yn)T,Z=(Z1,Z2,…,Zn)T,ε=(ε1,ε2,…,εn)T,X(t)=(X1(t),X2(t),…,Xn(t))T.模型(1)可以表示为:
(2)
其中:随机误差ε~N(0,σ2In),In是n维单位矩阵.
类似于Xu和Zhang[16],假设模型方差为异方差,并且利用一些解释变量将方差参数建模为如下形式,即:
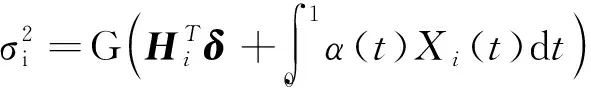
(3)
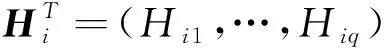
(4)
为了叙述方便,模型(4)可以简化为如下形式,包括均值模型和方差模型:
(5)
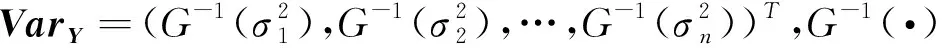
1.2 似然函数
令{(Yi,Zi,Hi,Xi),i=1,…,n}是来自模型(4)的独立同分布样本.定义函数型变量X(t)的协方差函数和经验协方差函数分别为:
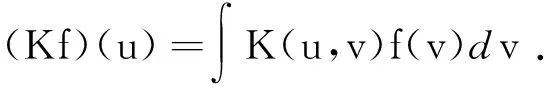
根据Karhunen-Loève表示定理可得:
(6)
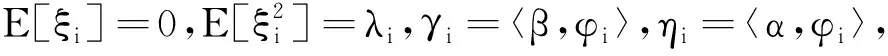
(7)
因此,双重部分函数型回归模型可以近似为:
(8)
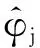
(9)
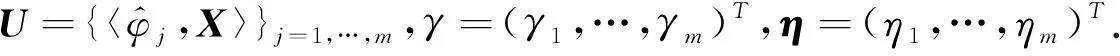
那么根据模型(9)可以得到似然函数:
(10)
其中V=Y-Zθ-Uγ.
2 贝叶斯估计
2.1 先验分布
为了应用贝叶斯估计方法,首先需要给出未知参数的先验分布,具体为θ~N(θ0,Bθ),γ~N(γ0,Bγ),δ~N(δ0,Bδ),η~N(η0,Bη),其中θ0,γ0,δ0,η0,Bθ,Bγ,Bδ和Bη是已知的超参数.那么参数Θ=(θT,γT,δT,ηT)的联合先验分布为:
π(θ,γ,δ,η)=p(θ)p(γ)p(δ)p(η)
(11)
其中p(θ)表示参数θ的先验概率密度函数.
2.2 贝叶斯后验推断
基于似然函数(10)和联合先验分布(11)就可以获得参数Θ=(θT,γT,δT,ηT)的联合后验分布p(Θ|Y,X,H,Z),具体如下:
p(Θ|Y,X,H,Z)∝L(θ,γ,δ,η|Y,Z,H,X)π(θ,γ,δ,η)
(12)
基于上式直接进行抽样和后验推断是比较困难的.为了解决这个问题,首先需要推导获得每一个未知参数的满条件分布,然后利用Gibbs抽样和Metropolis-Hastings抽样算法相结合的混合MCMC抽样算法来从各自的满条件分布中抽样,具体如下.
•θ的满条件分布:
(13)
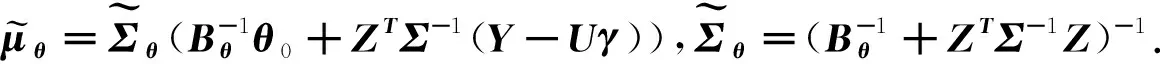
•γ的满条件分布:
(14)
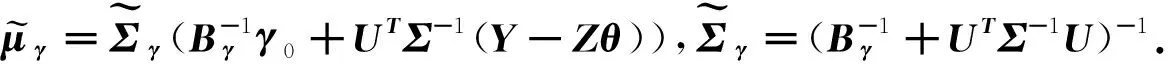
•δ的满条件分布:
p(δ|Y,Z,H,X,θ,γ,η)∝
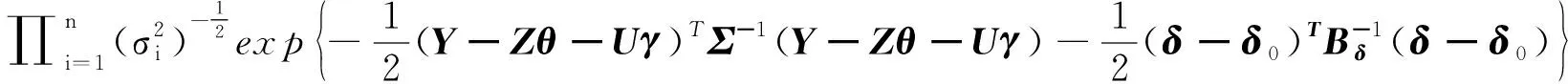
(15)
•η的满条件分布:
p(η|Y,Z,H,X,θ,γ,δ)∝
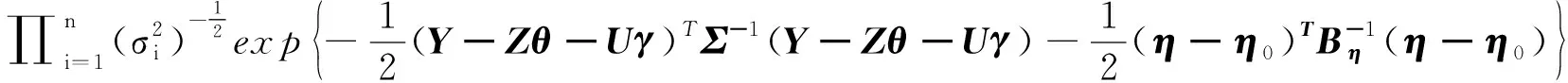
(16)
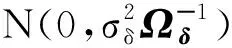
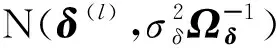
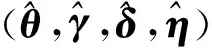

表1 未知参数Θ=(θ,γ,δ,η)的MCMC抽样算法Tab.1 An MCMC-based sampling algorithm for unknown parameters Θ=(θ,γ,δ,η)
3 模拟研究
这部分通过2个随机模拟例子来说明所提出的双重部分函数型回归模型和贝叶斯估计方法的有效性.
3.1 例1:双重部分函数型回归模型
数据从如下双重部分函数型回归模型中产生:
(17)
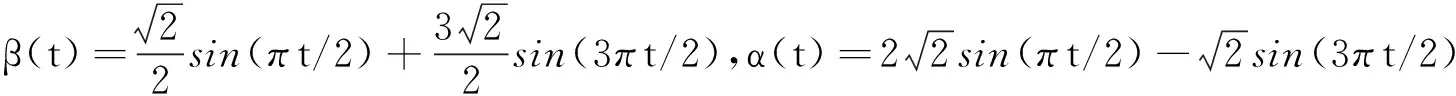
Case I:选取好的先验信息θ0=(1,-0.5,0.5)T,Bθ=0.25×I3,δ0=(1,-0.5,0.5)T,Bδ=0.25×I3.
Case II:选取无先验信息θ0=(0,0,0)T,Bθ=10×I3,δ0=(0,0,0)T,Bδ=10×I3.
Case III:选取不精确的先验信息θ0=3×(1,-0.5,0.5)T,Bθ=I3,δ0=3×(1,-0.5,0.5)T,Bδ=I3.
其他超参数设置为γ0=0m,Bγ=10×Im,η0=0m,Bη=10×Im,这也表示选取比较弱的先验信息,其中0p表示全是0的p维向量.在模拟中分别令样本量n=200,n=400和对于每一种情形下重复计算100次.
在上面设置的各种模拟环境下,应用Gibbs抽样和 Metropolis-Hastings算法相结合的混合MCMC算法来计算未知参数和函数型系数的贝叶斯估计.对于每次重复产生的每一次数据集,MCMC算法的收敛性可以通过EPSR值来检验[18],并且在每次运行中观测得到在 3 000 次迭代以后EPSR值都小于1.2.因此在每次重复计算中丢掉前 3 000 次迭代以后再收集J=2 000 个样本来产生贝叶斯估计.参数贝叶斯估计的模拟结果概括在表2~表3中. 另外,为了测量函数型系数估计的好坏,选择用如下定义的RASE来衡量精确度:
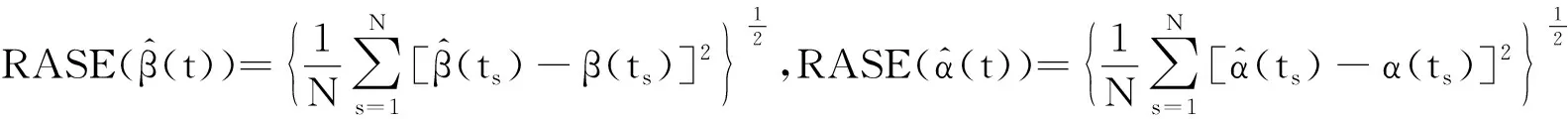
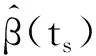
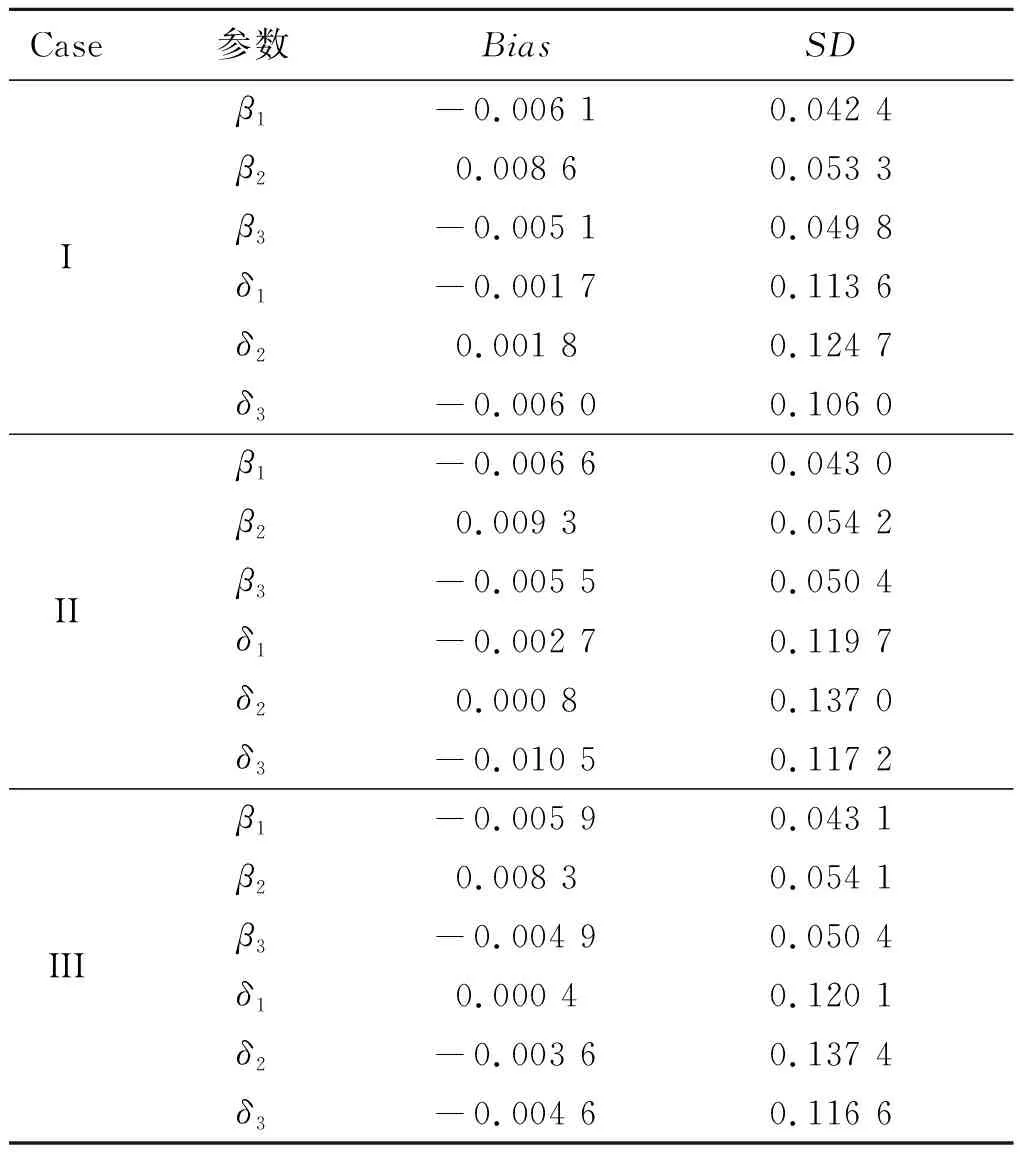
表2 例1中当样本量n=200和不同的先验分布情况下未知参数的贝叶斯估计结果
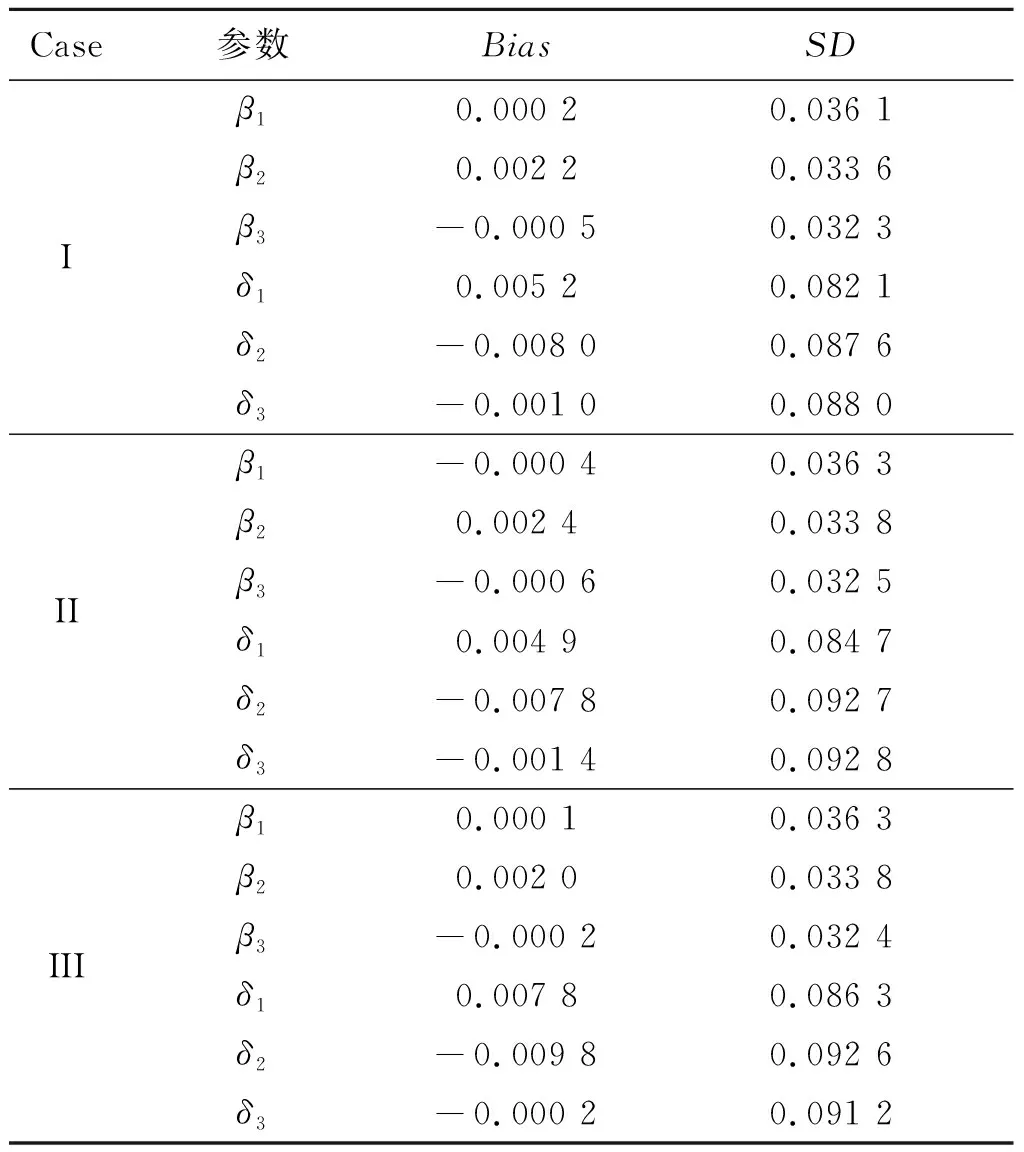
表3 例1中当样本量n=400和不同的先验分布情况下未知参数的贝叶斯估计结果
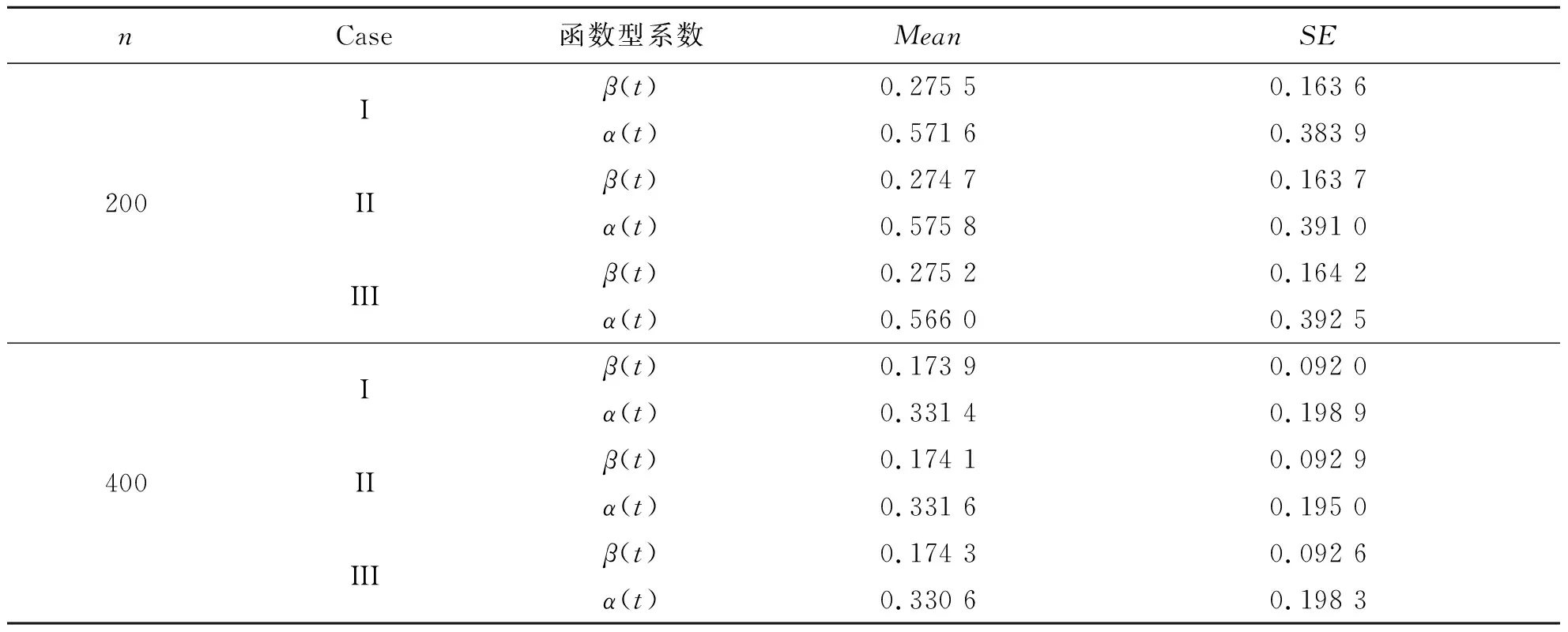
表4 例1中在不同的样本量下和不同的先验分布情况下函数型参数β(t)和α(t)的RASE的平均值和标准差
在表2~表3中,“Bias”表示基于100次重复计算未知参数的贝叶斯估计和真值之间的偏差,“SD”表示未知参数贝叶斯估计的标准差.从表2~表4中可以得到以下结论:1)在参数估计的偏差Bias和SD值方面,不管何种情形下贝叶斯估计都相当精确,并且随着样本量的增大,模型中参数部分和函数型系数部分的贝叶斯估计结果变得越来越好.2)在不同的先验分布下,贝叶斯估计结果表现得都差不多,这也说明提出的贝叶斯估计方法对先验分布的选取不是特别敏感.3)均值模型中参数估计的结果比方差模型中的参数估计效果要好一些.4)随着样本量的增大,RASE值的平均估计和标准差都变得越来越小,这也表明函数型系数估计得越来越好.从图1和图2中也展示了估计出来的函数型系数的曲线与相应的真实函数的曲线逼近得都比较好,这与表4展示出来的结果是一样的.总之,所有以上的模拟结果可以反映出所提出的贝叶斯估计方法能很好地恢复双重部分函数型回归模型中的真实信息.
3.2 例2:纯粹的双重函数型回归模型
在这个例子中,从如下纯粹的双重函数型回归模型中产生数据:
(18)
其中有关参数的设置和模拟环境与例1中一样.另外,在这个例子中仅考虑无先验信息以及所有的贝叶斯分析结果展示在表5中,其中为了节省空间和避免累赘,函数系数曲线估计图在此省略.从表中的结果可以发现,和预期的一样,在这种模型下应用提出的贝叶斯分析方法和例1中结果相似,且获得的结果也是令人满意的.这也说明提出的贝叶斯估计方法也适应于纯粹的双重函数型回归模型.

表5 例2中在不同的样本量下函数型参数β(t)和α(t)的RASE的平均值和标准差
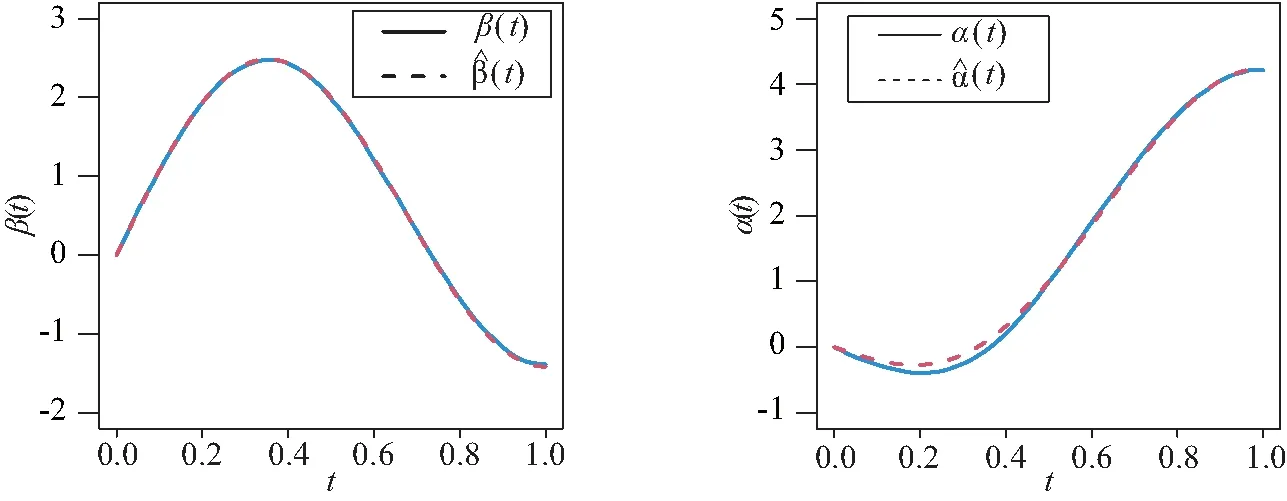
图1 例1中当n=200和Case II先验信息下函数型系数β(t)和α(t)的真实函数曲线和平均估计曲线
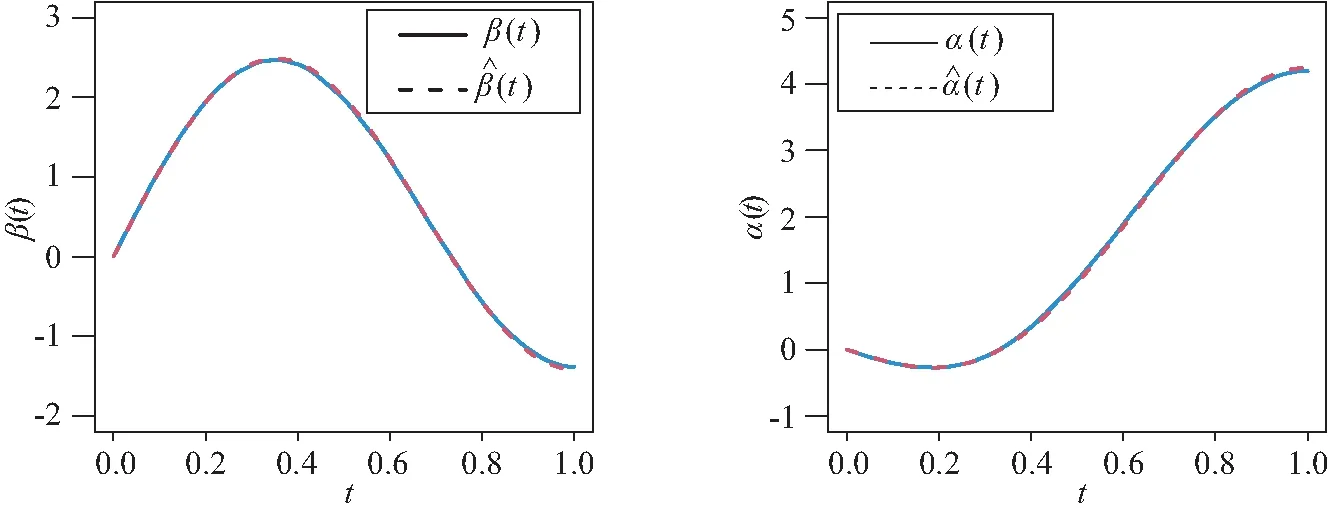
图2 例1中当n=400和Case II先验信息下函数型系数β(t)和α(t)的真实函数曲线和平均估计曲线
4 实际数据分析
这部分将提出的双重函数型回归模型应用到Growth数据集.该数据集描述了125个国家1961年到1985年的宏观经济数据.记Y表示1985年的人均GDP的对数,X(t)表示1961年到1985年年度储蓄率,由真实投资与真实GDP比值得到.首先基于1985年的人均GDP及其对数的数据给出散点图,如图3所示,通过散点图可以发现数据存在较显著的异方差性.另外,在这主要想研究历史的储蓄率对1985年的人均GDP的影响,因此考虑如下双重函数型回归模型:
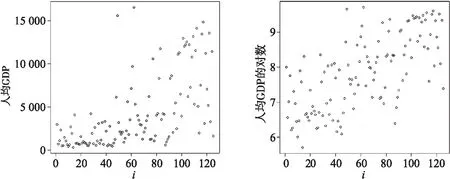
图3 人均GDP的散点图和对数的散点图
其中采用无信息先验以及截断参数选取和模拟研究中一样.另外,为了测试算法的收敛性,画出了所有未知参数的EPSR值的图, 且列在图4中.从图4中也能看出 3 000 次迭代以后所有参数的EPSR值都小于1.2,且接近1, 这表示 3 000 次迭代以后算法收敛了.在这里收集 3 000 次以后的后验样本计算贝叶斯估计.这样就可以获得函数型系数β(t)和α(t)的曲线估计,如图5所示.从图5中可以看出,均值模型中函数型系数估计的曲线和方差模型中的函数型系数估计曲线很相似,总体上都随着时间的推后而增加,在1982年达到最大,之后略有下降.这也表明历史的储蓄率对1985年的人均GDP总体上影响是正向的关系.
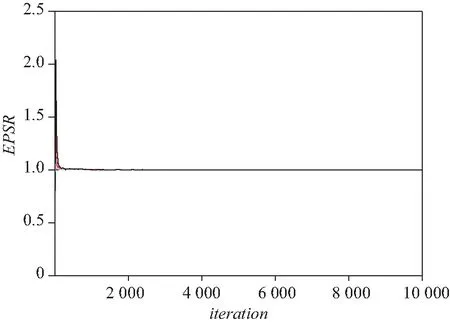
图4 实际数据分析中所有参数的EPSR值Fig.4 EPSR values of all parameters in real data analysis
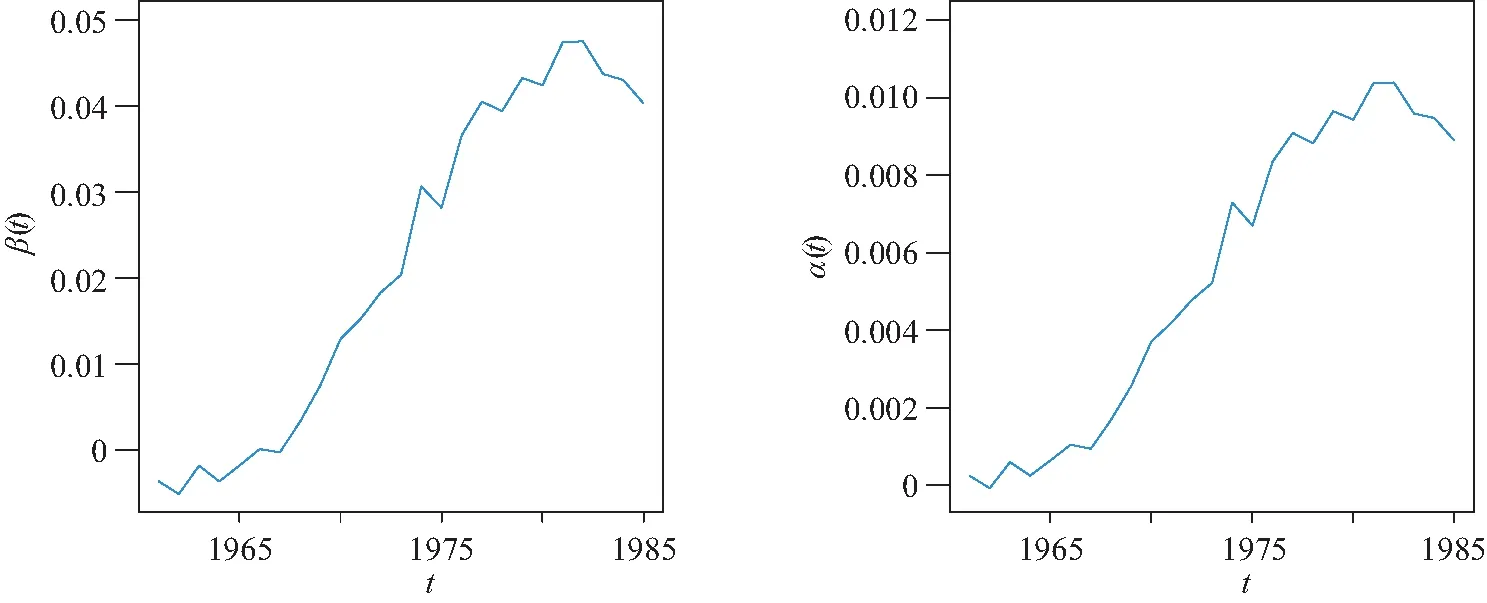
图5 实际例子中函数型系数β(t)和α(t)的真实函数曲线和平均估计曲线
5 结 论
针对异方差函数型数据,本文基于方差建模的思想提出了双重部分函数型回归模型,其中使用函数型协变量对方差参数进行建模.另外,运用Karhunen-Loève表示定理来逼近函数型系数,以及基于给定的先验分布可以获得未知参数的联合后验分布和各个参数的条件分布,然后应用Gibbs抽样和Metropolis-Hastings算法相结合的混合MCMC算法来同时获得均值模型和方差模型中未知参数和函数型系数的贝叶斯估计.模拟研究显示:1)随着样本量的增大,模型中参数部分和函数型系数部分的贝叶斯估计结果都是越来越好;2)贝叶斯估计方法对先验分布的选取不是特别敏感;3)均值模型中参数估计的结果比方差模型中的参数估计效果要好一些.另外,将提出的双重函数型回归模型应用到Growth数据集,研究了历史的储蓄率对1985年的人均GDP的影响.两个随机模拟研究例子和实际数据分析都表明所提出的双重部分函数型回归模型和贝叶斯估计方法是可行有效的.
