直升机卫星通信旋翼遮挡问题仿真评估方法
2022-11-10张学生崔建华瞿俊杰
陈 刚,张学生,崔建华,瞿俊杰
(上海清申科技发展有限公司,上海 201306)
1 研究背景
直升机被广泛应用于军事和民用各领域,承担着物资运送、应急抢险救灾、搜索救援、重大事件安保等任务,由于直升机执行任务的复杂性,全航程高可靠性通信是一个难题,利用卫星进行通信是解决直升机通信难题的手段之一。针对直升机卫星通信问题,围绕直升机旋翼遮挡的信道编码、前向链路和返向链路通信策略等方面已有大量研究成果[1][2][3][4]。近几年,随着卫星技术的发展,直升机通信速率大幅提高,国外利用静止轨道通信卫星可实现的最大通信速率已达到10 Mbps[5],国内已达到2 Mbps[6]。
随着高通量卫星通信技术的成熟[7],以及低轨宽带卫星星座的发展[8],宽带卫星通信系统和通信终端设备发展迅猛[9]。基于直升机气动特性的考虑,直升机宽带卫通天线一般安装在旋翼下方靠近尾翼的机身处,因此卫通天线会受到旋翼遮挡的影响[4][10][11]。对直升机旋翼遮挡的信道特征评估主要通过通信试验方法来获取。由于直升机卫星通信场景复杂,飞行测试成本高,需要提前对旋翼遮挡程度进行预分析评估,用于通信试飞方案设计。特别是对低轨通信卫星,通信时段和时长受限,方位角和高度角随卫星运动而变化,旋翼遮挡问题分析更为复杂。因此,本文提出采用计算天线遮挡面积占比(遮挡率)的方法来满足不同轨位卫星通信时的旋翼遮挡问题分析的需求。本文给出了完整的遮挡率计算数学模型,完成了仿真系统算法设计,最后给出了一个静止轨道卫星和低轨卫星对比分析的应用案例。
2 遮挡率计算方法
2.1 遮挡问题分析
如图1所示,旋翼对安装在旋翼下方的天线沿通信波束视线方向形成遮挡,天线遮挡面积的大小由波束入射方向、旋翼尺寸、旋翼方位、飞行姿态、天线安装位置、天线尺寸等因素决定。旋翼尺寸、天线安装位置、天线尺寸为固定参数;波束入射方向与直升机和卫星相对位置相关;旋翼方位因旋翼的旋转运动而呈现周期性变化特点;直升机飞行姿态与飞行任务有关,可以由姿态测量传感器实时获取。

图1 旋翼遮挡示意
对于静止轨道卫星,由于星地距离大(静止轨道卫星高度为36 000 km),在一定区域范围内通信波束方位角和波束角的变化幅度不大,旋翼遮挡的动态影响因素主要为飞行姿态。
对于非静止轨道卫星,卫星按照预定轨道飞行,卫星位置随时间变化,通信所在区域需满足波束高度角大于10°的建链条件,通信时间段受卫星轨道地面高度角约束。特别是低轨卫星(高度小于1 000 km),在通信时间段内,通信波束方位角和高度角随卫星位置不同而呈现较大幅度的变化,旋翼遮挡的动态影响因素必须同时考虑卫星的位置变化。如图2所示,卫星在位置1和位置2时,通信波束相对旋翼的入射角和不同,会造成旋翼对天线的遮挡面积不同。
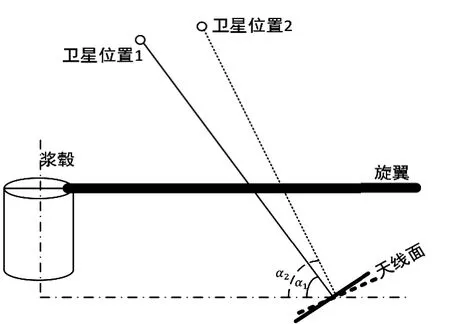
图2 卫星位置变化关系
试验表明,在全遮挡情况下,信号衰减幅度可以达到15 dB[12]。如图3所示,由于旋翼的转动,天线受遮挡呈现周期性特点,在一个遮挡周期内,可以分为不遮挡、部分遮挡、全遮挡三种情况,遮挡周期与旋翼数量和转速有关。直升机旋翼转速通常在每分150转以上,可知旋翼转动一周时长小于400 ms,2旋翼直升机遮挡周期小于200 ms,4旋翼直升机遮挡周期小于100 ms。在旋翼转动一周的时长内,直升机和卫星的位置变化引起的波束指向变化可以忽略不计,因此本文采用旋翼转动一周的平均遮挡率来进行遮挡程度的量化评估。

图3 遮挡状态变化周期
2.2 遮挡数学模型
2.2.1 遮挡投影关系模型
在通信过程中,天线伺服控制系统始终控制天线指向卫星,如图4所示,卫星波束矢量始终垂直于天线面,旋翼对天线的遮挡面积是旋翼沿波束方向到天线面的投影面积,定义旋翼在天线面上的投影面积占天线面面积的比率为遮挡率,采用遮挡率对遮挡程度变化情况进行量化分析。

图4 投影变换模型

图5 旋翼面内投影
2.2.2 坐标转换计算模型
坐标投影转换时需要在同一坐标系下进行,考虑利用旋翼转动的周期性特点,为方便计算,如图6所示,定义旋翼面坐标系为:原点在旋翼平面内位于旋翼的中心,X轴在旋翼平面内指向机头方向,Z轴垂直旋翼平面指向下方,Y轴在旋翼平面内指向右方构成右手坐标系。投影变换和遮挡率计算统一在旋翼面坐标系下进行。

图6 投影坐标计算

为描述天线面上的点坐标和天线指向,定义天线面初始参考坐标系为原点在天线平面内位于天线面的中心位置,X轴、Y轴、Z轴指向与旋翼面坐标系一致,天线面初始参考坐标系与旋翼面坐标系固联于机体上。初始状态下,天线面本体坐标系与天线面初始参考坐标系一致,设天线面参考坐标系下点A坐标记为 ,天线面法线垂直天线面向上,初始状态法向矢量记为,伺服控制系统控制天线面始终对准卫星,即天线面法线与波束矢量始终保持一致。设t时刻坐标系下的波束矢量为,天线面法向矢量为,则:




机体姿态运动变化关系用导航坐标系到机体坐标系的欧拉角转换关系来描述,设X轴、Y轴、Z轴对应的姿态欧拉角分别为则机体坐标系到导航坐标系的转换关系矩阵为:

设t时刻导航坐标系下卫星位置坐标为,直升机位置坐标为,则导航坐标系下的波束矢量为


因为天线面初始参考坐标系与旋翼面坐标系坐标轴指向一致,所以,


进而可以利用公式(1)求取t时刻点A沿波束矢量方向到旋翼面内的投影点坐标。
2.3 遮挡率仿真计算过程
场景仿真分析时,按以下步骤生成仿真所需数据和进行遮挡率计算:
(1)由飞行任务规划软件生成t时刻直升机位置坐标数据和飞行姿态数据。
(2)由卫星轨道计算软件生成t时刻卫星位置坐标数据。
(3)由直升机位置坐标数据建立导航坐标系,转换得到导航坐标系下的卫星和直升机位置坐标值,并生成t时刻波束矢量数据。
(4)根据天线尺寸生成天线面初始参考坐标系下的天线面轮廓线采样点坐标数据,按上一节所述计算模型计算t时刻天线面轮廓线采样点到旋翼面的投影轮廓线坐标。
(5)由旋翼初始位置和转速获取t时刻旋翼位置,生成旋翼轮廓线坐标。-
(6)在旋翼平面内,采用网格法计算天线面轮廓线所围区域面积,以及旋翼轮廓线与天线面轮廓线所围区域重叠部分面积。
(7)重叠部分面积除以天线面区域面积即得到t时刻的遮挡率。图7为仿真算法设计流程图。

图7 仿真算法设计流程图
3 仿真分析案例
利用上节所述算法,通过计算旋翼转动一周的平均遮挡率来进行直升机在不同飞行方位航向和飞行仰角下的遮挡问题分析。
仿真参数如表1所示,分别选择了一颗静止轨道卫星(卫星1)和一颗低轨卫星(卫星2)进行遮挡问题分析。

表1 仿真参数
卫星1为静止轨道卫星,可以近似认为飞行区域空间波束矢量保持不变,首先分析平飞时,遮挡率随方位角的变化关系,分析结果如图8所示。从图中可以看出,该区域内直升机在平飞状态下,最大平均遮挡率为16.3%,此时直升机方位角为144°,与该区域对星方位角吻合,此时直升机朝向卫星方向水平飞行。

图8 遮挡程度随航向变化(卫星1)
进一步可以选择任意方位航向,进行不同飞行仰角下的遮挡问题分析。图9为直升机在145°方位航向上飞行时,不同仰角下天线受遮挡程度的变化情况。可以直观看出,在该航向上俯冲飞行时,天线始终受到旋翼遮挡,遮挡率随俯冲角的增大而缓慢变小,最小遮挡率约为8.8%;在该航向上爬坡飞行时,遮挡率随仰角增大而快速增加,在16°仰角时天线被完全遮挡,主要原因为天线指向靠近浆毂,旋翼缝隙变小,最终被浆毂完全遮挡。仿真中仅考虑旋翼遮挡,没有考虑浆毂和机体遮挡,所以30°仰角之后天线遮挡率变为零,天线对准卫星方向在旋翼平面下方。在飞行仰角超过16°之后,由于受到浆毂或机体遮挡,天线已处于100%遮挡状态,工程应用中可以参考上节模型和算法增加浆毂和机体遮挡部分,或者加上天线转动角度阈值,使其不能指向旋翼下方。
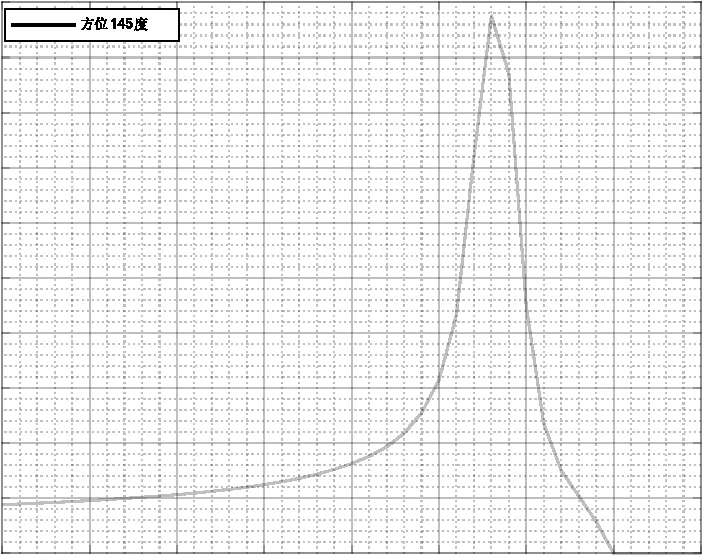
图9 遮挡随仰角变化(卫星1)
卫星2为低轨卫星,直升机所在区域内卫星高度角大于10°的时间段内才能建立视距通信链路。图10为直升机所在的位置区域,卫星2的方位角和高度角变化情况。在仿真时间段内,高度角大于10°的时长为469 s,该时间段内卫星方位角的变化范围在-120°至78°之间。由于卫星2的空间位置随时间快速变化,空间波束矢量也随时间快速变化,图11分别选择了直升机平飞时在0°、45°、90°、135°、180°、225°、270°、315°等8个方位航向上遮挡率随时间的变化关系进行呈现。从图中可以看出,对低轨卫星,直升机在不同方位方向上平飞时,在通信时间段内遮挡率随卫星运动呈现不同的变化特征,部分时间段内无遮挡,部分时间段内遮挡严重。例如,在与卫星2通信时,在方位45°航向平飞时,前180 s无遮挡问题,之后出现遮挡问题,并在380 s附近时遮挡率达到最大值(超过30%),之后遮挡率快速下降。
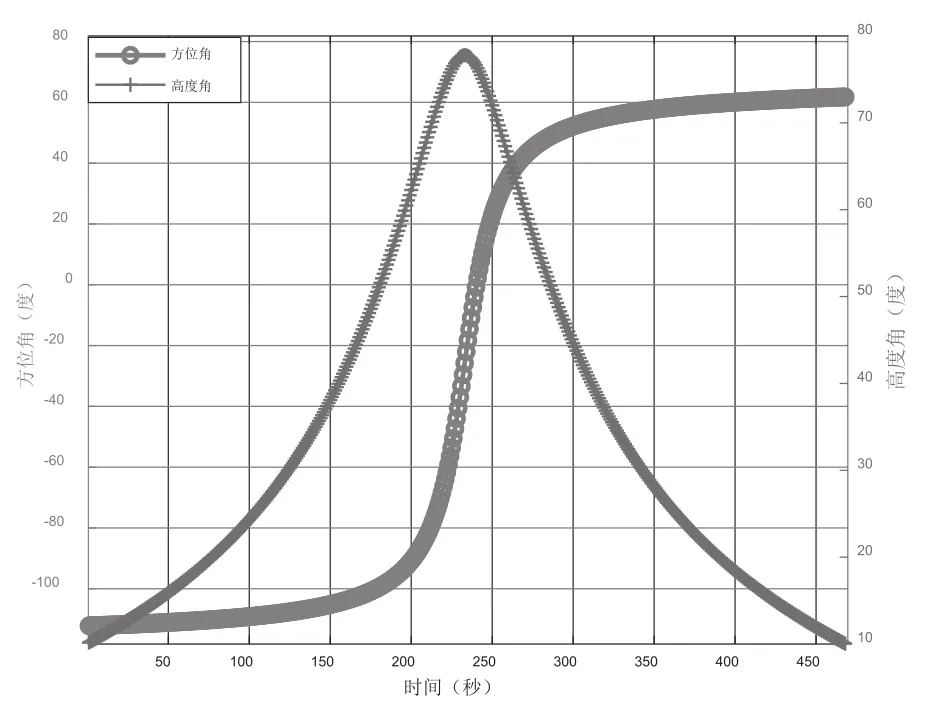
图10 卫星2方位角和高度角变化

图11 遮挡程度随航向变化(卫星2)
通过对比图11和图8可以发现,同一区域内直升机平飞时,静止轨道卫星和低轨卫星在不同航向呈现完全不同的特点,例如,在0°方位航向时,与卫星1进行通信时完全不存在遮挡问题,并且没有通信时间段约束,但与卫星2进行通信时,除受通信时间段约束外,还在部分时间段内存在遮挡问题。
同样,对低轨卫星2也可以像图9一样生成直升机在不同飞行仰角下的遮挡率变化情况,以及增加直升机侧倾角,本文不再赘述。
4 结束语
对直升机卫星通信过程中存在的旋翼遮挡问题,本文提出一种遮挡率计算方法,用来对飞行过程中的旋翼遮挡严重程度进行仿真分析评估。利用本文中的模型和算法,分别对静止轨道卫星和低轨卫星案例进行了仿真分析,结果表明该方法可以直观评估出不同轨位卫星,不同飞行姿态下天线受旋翼遮挡情况。该仿真分析评估方法可以用于优化天线尺寸设计,天线安装位置选择,以及通信试飞试验前的预分析评估等,具有较高的实际工程应用价值。■
