面向百兆瓦级应用的电池储能系统拓扑与控制方法
2022-11-09谷晴李睿蔡旭谢宝昌
谷晴,李睿,蔡旭,谢宝昌
(电力传输与功率变换控制教育部重点实验室(上海交通大学),上海市 闵行区 200240)
0 引言
近年来,人们生产生活对于能源的需求日益提高,随着传统化石能源的储量不断减少,风、光等新能源凭借其可再生、无污染等特点得到广泛关注和应用[1]。然而,与传统化石能源发电相比,新能源发电具有随机性、间歇性和波动性的特点,这会导致一系列的发电出力不连续、功率波动等问题,在并入电力系统时,对电力系统的稳定性造成影响。2022年7月,中国电力企业联合会发布的《2022年上半年全国电力供需形势分析预测报告》[2]显示,截至2022年6月底,全国全口径发电装机容量为24.4亿kW,其中,非化石能源发电装机容量为11.8亿kW,同比增长14.8%,占总装机容量的48.2%。随着新能源发电装机容量不断提升,其对电力系统运行稳定性的影响越来越不容忽视。电池储能系统(battery energy storage system,BESS)可以根据供需情况,将能量以电能的形式吸收、储存和释放,平滑功率波动,为电力系统对高比例新能源发电的消纳提供了有效的解决途径[3-5]。随着新能源占总装机比重的不断提高,电池储能电站的容量和规模不断扩大,已进入百兆瓦级并向吉瓦级发展。
电池储能电站包含若干BESS单机,为适应电池储能电站大容量的需求,增加单机数量和提升单机容量为2种有效途径。然而,随着单机数量的增加,集电系统复杂性升高,且多机并联易产生一系列稳定性问题[6],协同控制困难。因此,面向百兆瓦级乃至吉瓦级电池储能电站,需要提升BESS单机容量,减少并联单机数量,简化结构。
传统集中式BESS的电池堆经过三相两电平功率变换系统(power conversion system,PCS)[7]、升压变压器接入电网。该拓扑具有结构简单、开关器件少、易于控制等优势,但也存在一些问题。
电池堆为了获得较高的输出电压和容量,需要大量电池单体进行串并联,电池单体之间的不一致性易造成过充、过放[8],使电池堆整体输出性能下降,甚至影响电池单体的寿命,这种短板效应会随着电池单体数量的增加而不断加深。另外,为了实现系统的安全运行,需要电池管理系统(battery management system,BMS)对电池堆予以监测、均衡,而数量过多的电池单体给BMS造成较大的管理压力。同时,集中式的分布形式使得电池堆局部故障容易扩散,扩容困难,随着电池单体数量的增多,系统维护难度加大,安全性降低。因此,电池堆的输出电压等级和容量的提升受限。根据国际电工技术委员会制定的标准[9],单个电池堆的最大电压为1 500 V。目前,传统集中式BESS的单机容量多为0.63 MW,一般不超过1 MW。
受到电力电子器件耐压水平的限制,变换器的输出电压等级较低,传统集中式BESS为了获得较高的电压等级,需要通过升压变压器接入电网,能量传递环节较多,中间通信时间延时较长,且变压器损耗较大,使系统效率降低。
由于三相两电平变换器输出电平数量较少,交流侧谐波含量较高,需要大容量滤波装置满足并网需求[10],增大了系统体积。
综上所述,传统集中式BESS适用于发电侧或用户侧等低压、小容量应用场合,但是对于电网侧高压、大容量应用场合,传统集中式BESS的电池堆输出电压等级和容量的提升受限,响应延时明显,效率低,电能质量较差,体积大,难以应对电池储能电站日趋大容量、规模化的挑战。
针对传统集中式电池储能系统存在的问题,高压直挂式BESS受到广泛关注,成为研究热点。在结构上,高压直挂式BESS从集中式结构转变为模块化分布式结构,通过若干子模块(submodule,SM)级联升压,达到需求电压等级,再经过滤波器并网。与传统集中式电池储能系统相比,高压直挂式BESS具有明显优势。
通过子模块级联升压,储能系统不再受到单个电池堆输出电压等级和容量的限制,随着子模块数量的增加,可达到较高输出电压等级,满足高压和大容量应用的需求,扩容灵活。另外,电池单体分散于各SM中,BMS分割管控,均衡、管理难度降低,在系统发生局部故障时,可切除故障SM,将其隔离检修[11]。同时,无需变压器和大容量滤波装置,便可实现中高压并网,系统体积相对较小。
高压直挂式BESS的典型拓扑主要有星型结构[12]、三角形结构和模块化多电平(modular multilevel converter,MMC)结构[13-14]3种。在3种结构中,星型结构为最基本的结构,其他结构可由此推演得到。
面向电池储能电站大容量、规模化的需求,目前的研究多集中于单机数量的增加。为探究在单机容量和扩容方面更具优势的BESS拓扑,本文首先通过计算对比分析了星型结构、三角形结构和MMC结构的单机容量;然后以星型结构为例,介绍了其拓扑结构和数学模型,分析了高压直挂BESS的控制策略,包括网侧功率控制和荷电状态(state of charge,SOC)均衡控制,并通过仿真验证了控制策略的有效性。
1 高压直挂BESS容量分析
图1为高压直挂BESS的星型结构,SM由H桥(H bridge,HB)变换器、滤波电容和若干串联的电池单体组成。每个H桥中包括4个绝缘栅双极型晶体管(insulated-gate bipolar transistor,IGBT),为估算单机BESS的容量,令IGBT的电压等级为Vsmax,系统的电压等级为Vl,则每相的SM数量NSM可以表示为

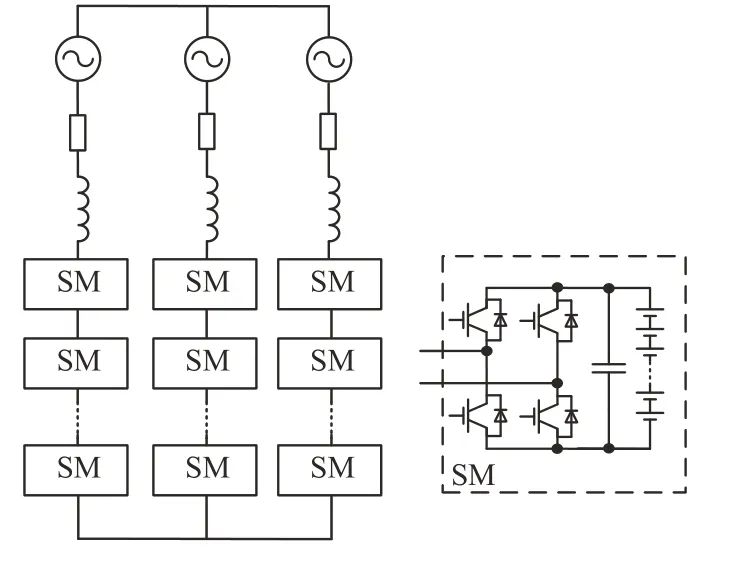
图1 星型结构Fig.1 Star structure
每个SM中包含若干串联的电池单体,单个SM中的电池单体数量Nbat可以表示为

式中:Vbmin为电池单体的最低电压;kv为电压裕量。
为保证电池单体与电网之间能够正常地进行能量交换,H桥直流侧电压要高于交流侧电压,因此kv的取值一般为1.05~1.15。则单机容量Ssys可以表示为
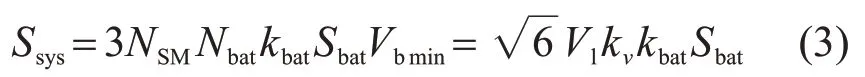
式中:kbat为电池单体充放电倍率;Sbat为电池单体额定容量。可以看出,Vsmax和Vbmin并不是影响Ssys的决定性因素,可以通过改变NSM和Nbat,使交流侧输出电压达到系统的电压等级。
目前常用于储能的电池单体容量为280 A·h,取充放电倍率为0.5 C,电压裕量为1.15,代入式(3),可以得到35 kV的高压直挂BESS星型结构的单机容量约为14 MW。
对于三角形结构和MMC结构,该单机容量的分析过程同样适用,其单机容量可以通过星型结构的分析结果推演得到。
图2为高压直挂BESS的三角形结构,其SM与星型结构一致。由于三角形结构线电压为相电压的1.732倍,因此,在系统电压等级和SM规格相同的情况下,三角形结构的SM数量为星型结构的1.732倍,单机容量也扩展到1.732倍,约为24 MW。

图2 三角形结构Fig.2 Triangular structure
图3为高压直挂BESS的MMC结构,其SM有2种结构,一种为基于H桥的SM结构,与星型结构一致;另一种为基于半H桥的SM结构。MMC结构由2个星型结构并联构成,每一相具有上下2个桥臂,在系统电压等级和SM规格相同的情况下,当SM中的变换器为H桥时,SM数量为星型结构的2倍;当SM的变换器为半H桥时,由于半H桥不能输出负电平,因此SM数量为星型结构的4倍[15]。基于半H桥SM结构的输出电压相当于在基于H桥SM结构的输出电压上叠加了一个直流偏置,以达到相同电压等级。因此,MMC结构的单机容量也相应扩展到原来的2倍、4倍,分别约为28、56 MW。

图3 MMC结构Fig.3 MMC structure
通过对比,高压直挂BESS三种结构的单机容量远高于传统集中式BESS,在组成电池储能电站时,单机数量更少,结构简化,控制复杂性降低,更加适用于高压、大容量的应用场合。
2 高压直挂BESS的星型结构
2.1 拓扑结构
高压直挂BESS的星型结构如图4所示,呈三相星形连接,每一相由N个模块级联构成,经电感Lg接入电网。Lg为滤波电感,用以滤除电网侧电流所含谐波[16],改善电能质量;Rg为滤波电感的寄生电阻。SM包括功率模块和电池模块,其中,功率模块由H桥变换器和滤波电容Cb构成,负责电网与电池模块之间的能量交换。电池模块由若干个电池单体串联而成,是能量储存的载体,按照功率模块的调控,进行充放电行为。

图4 高压直挂式BESS的星型结构Fig.4 Star structure of high voltage transformerless BESS
2.2 数学模型
N个功率模块级联连接,功率模块交流端为电网侧,直流端为电池侧,级联后第k相功率模块电网侧的输出电压vk由N个功率模块的输出叠加得到,如式(4)所示:

式中skj为第k(k=a,b,c)相第j个功率模块的开关函数,如式(5)所示:

由于电路呈三相星型连接,根据基尔霍夫电压定律和基尔霍夫电流定律,电网侧的电压电流关系如式(6)所示:

式中:ek为第k相电网电压;ik为第k相电网侧电流;vO'O为系统的零序电压分量。
由式(6)可以推导出vO'O的表达式为

vO'O由电网电压和功率模块电网侧的输出电压所决定[17]。当电网电压三相对称,且没有通过功率模块注入零序电压时,系统的零序电压分量为0。此时式(6)可以简化为
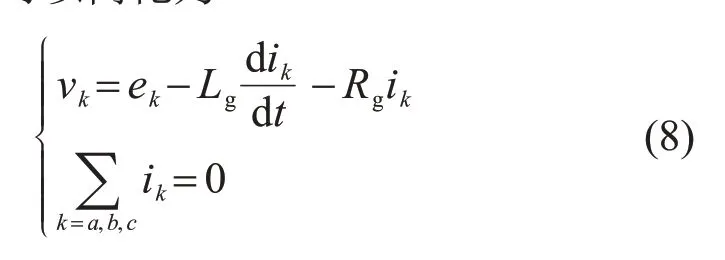
第k相第j个电池模块的荷电状态为SOCkj,则第k相和整个系统的荷电状态如式(9)所示:
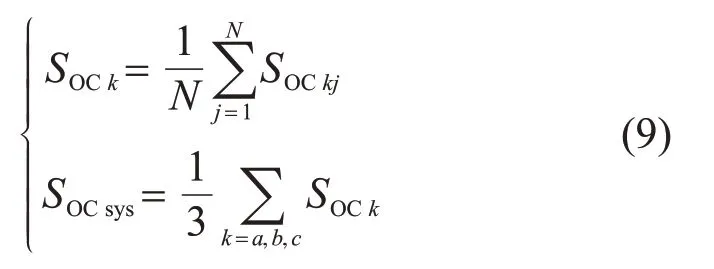
为了更加直观地表示各相荷电状态的不均衡程度,定义第k相SOC不均衡度为

3 高压直挂BESS的控制策略
3.1 网侧功率控制
网侧功率控制是高压直挂BESS的基本功能之一,根据控制对象的不同,可以分为电压源型控制和电流源型控制。电压源型控制通过模拟同步发电机的调压、调频特性,控制功率模块电网侧的输出电压,实现对功率的调节,同时为电网电压及频率提供支撑作用[18]。但电压源型控制环路中存在较大的惯性延迟,响应速度较慢。相比之下,电流源型控制在应对功率波动等暂态情况时,具有更快的响应速度,被广泛应用于储能系统的控制中。其中,电流解耦控制是最常见、最可靠的控制方法之一[19-20]。通过Clark变换和Park变换,将三相静止坐标系下的交流量转换到两相旋转坐标系下的直流量,简化了控制器的设计。对式(8)作变换,可以得到dq坐标系下的电压电流关系,如式(11)所示:

其中,T(θ)3s-2r为变换矩阵,如式(12)所示:

可以看出,dq轴之间存在电感耦合项,相互之间并不完全独立,即在调节d轴电流分量的过程中,q轴电流也会受到影响,反之亦然。并且影响程度与频率成正比例关系,系统频率越高,耦合程度越高[21]。因此,为了消除耦合项的影响,需要引入电感交叉解耦项。同时,电网电压作为扰动分量,需要引入电网电压前馈解耦项。
θ通过锁相环(phase locked loop,PLL)获得,PLL以功率模块电网侧的输出电压q轴分量vq为控制对象,通过PI控制器得到一个使得vq为0的角度θ,此时d轴分量vd与功率模块电网侧的输出相电压幅值相等,据此可以得到dq轴电流分量的参考值。带有PLL的电流解耦控制如图5所示。其中:P0、Q0分别为参考有功、无功功率;Vl为功率模块电网侧输出线电压的有效值;vsabc为控制变换器输出电压的参考信号。

图5 基于锁相环的电流解耦控制Fig.5 Current decoupling control with phase locked loop
为了验证该控制策略的正确性,利用Matlab/Simulink搭建35 kV/10 MW的高压直 挂 式BESS仿真模型进行验证,系统参数设置如表1所示。

表1 仿真参数Tab.1 Simulation parameters
仿真所得电压vabc、电流iabc和有功功率的波形如图6所示,可以看到,系统稳定运行,符合理论预期。

图6 电流解耦控制仿真波形图Fig.6 Waveforms of current decoupling control simulation
3.2 荷电状态均衡
对于星型结构,注入零序电压不会引入零序电流,电能质量得以保证。因此,考虑采用注入零序电压的方式实现SOC相间均衡。设注入的零序电压的表达式为
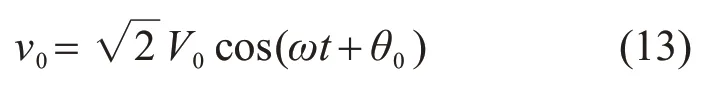
式中:V0为零序电压的幅值;ω为系统的当前实时角速度;θ0为零序电压的相角。则注入零序电压后的网侧三相电压的表达式如式(14)所示:

式中Vg为网侧三相电压的幅值。网侧三相电流的表达式为
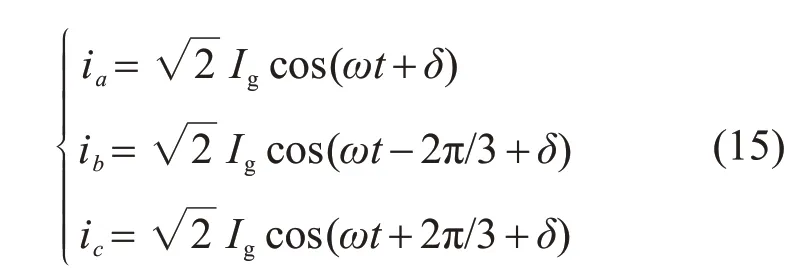
式中:Ig为网侧三相电流的幅值;δ为合成电流矢量与d轴的夹角,表达式为

三相功率的表达式为:

式中:ΔPa、ΔPb、ΔPc分别为a、b、c三相的附加功率,对其求和,可得
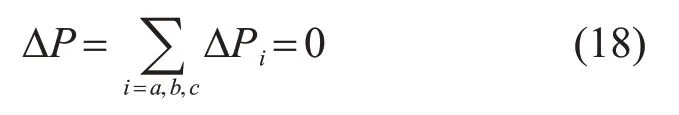
可以看出,注入的零序电压只会影响有功功率在三相之间的分配,而不会影响储能系统总功率。注入的零序电压会在各相产生附加功率,从而改变各相的有功功率,以实现SOC的相间均衡。SOC的不均衡度越大,所需的附加功率越大,因此,在控制中,使各相附加功率与SOC不均衡度呈正比关系。

式中λ为附加功率与SOC不均衡度的比例系数。由式(9)和式(10)可知,三相SOC的不均衡度有如下关系:

三相SOC不均衡度之和为0,三相对称电压、电流也具有三相分量之和为0的性质,该性质反映的是随着时间的变化,三相分量的瞬时值之和始终为0,本质上是标量的计算,是数值的相加减。但如果考虑空间相位,就不仅仅是数值的加减,而应该将各相分量放到abc三相坐标系中考虑,此时的合成矢量不再是0。通过类比,将三相SOC不均衡度视为a、b、c方向上的3个矢量,合成矢量ΔSOC的表达式为
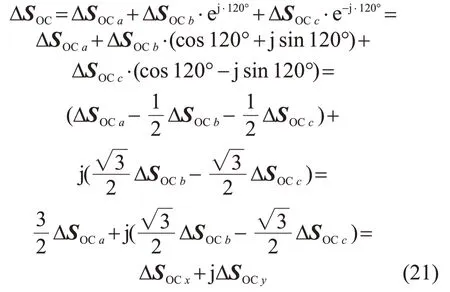
通过式(21)可以看出,合成矢量ΔSOC除了可以分解到abc坐标系,还可以分解到xy坐标系,其中,x轴与a轴重合,y轴由x轴逆时针旋转90°得到,如图7所示。

图7 合成矢量ΔSOC的分解Fig.7 Decomposition of synthetic vectorΔSOC
由式(21)可以得到如下对应关系:

合成矢量ΔSOC与x轴的夹角为γ。
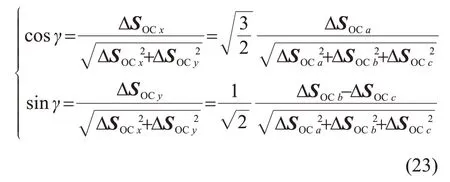
通过式(23)可以得到:

定义:

则附加功率式(19)可以表示为:

通过式(26)可以得到如下对应关系:

系统在稳态运行时,λ、Ig均为恒定值,因此可以得到注入零序电压的幅值和相位如式(28)所示,其中,K0为一比例系数。

图8为SOC相间均衡控制框图,为了验证该均衡策略的有效性,在2.1节所搭建的仿真系统上进行仿真验证。设置三相的SOC初始值分别为10%+0.1%、10%、10%-0.1%,设置系统在0.2 s时能使SOC相间均衡控制,所得仿真波形如图9、10所示。

图8 SOC相间均衡控制Fig.8 Clustered SOC balancing control

图9 三相SOC波形Fig.9 Waveforms of three-phase SOC

图10 零序电压的PWM波形Fig.10 PWM waveform of zero-sequence voltage
可以看到,从0.2 s开始,三相SOC差值逐渐减小,在4.5 s左右达到一致,并保持均衡状态稳定运行。随着三相SOC不均衡度的降低,由于零序电压的注入而产生的额外脉冲宽度调制(pulse width modulation,PWM)信号从0.2 s开始幅值不断衰减,在达到均衡后变为0。
4 结论
针对面向百兆瓦级应用的电池储能系统拓扑与控制方法展开了详细研究。通过计算,分析了35 kV下星型结构的单机容量,并将分析结果推演到三角形结构和MMC结构,结果表明:
1)3种高压直挂BESS可达到的单机容量远高于传统集中式BESS的单机容量,且扩容灵活,更加容易实现。
2)在构成同等规模的电池储能电站时,采用高压直挂BESS所使用的单机数量更少,结构得到简化,控制复杂性降低,高压直挂BESS更适用于高压、大容量的应用场合。
