强对流条件下使用p-VOF 方法的低温圆管二维结霜模拟

2022-11-09梁新刚徐向华

空气动力学学报 2022年5期

夏斌，梁新刚，徐向华，*

(1. 清华大学航天航空学院，热科学与动力工程教育部重点实验室，北京 100084；2. 中国空气动力研究与发展中心空气动力学国家重点实验室，绵阳 621000)

0 引言

英国反应发动机公司研发的协同吸气式火箭发动机（synergistic air-breathing rocket engine, SABRE）作为一种新型预冷组合式发动机的典型代表，被认为是未来20 年内最有可能实现单级入轨的动力系统[1]。由于SABRE 采用了先进的进气预冷却技术，提高了发动机进气量、增加了压缩机的压比和燃油加入量，其吸气模态的工作马赫数上限可提高到马赫数5[2]，能够顺利衔吸气模态和火箭模态，从而避免了动力模态衔接的推力陷阱问题。为了保证SABRE 在高马赫数下的进气量和推力，需要将来流冷却至最低-130℃[2]。然而，发动机吸气模态工作包线内12 km 左右的空域中含有大量水蒸气，如不采取有效的抑霜措施，这些水蒸气将在低温的预冷换热器表面结霜，并在数秒内将换热器堵塞[3]。因此，预冷换热器的抑霜技术是SABRE 的核心技术之一。然而，目前这种预冷器抑霜技术的具体技术途径未见诸报道。

虽然目前已有大量结霜抑霜的研究，但这些研究绝大多数是针对自然对流或低速流动条件且冷面温度高于-30℃的结霜[4-5]，而SABRE 的进气预冷器工作在来流速度很快（10 m/s 以上[1]）、冷面温度很低的环境。由于快速来流空气的作用，所结霜层较致密，不同于在自然对流或低速流动下所形成的晶枝结构和稀疏霜层[6]。这种预冷器的结霜也不同于飞机结冰，飞机结冰是液态过冷水滴撞击机翼表面凝固为冰的过程[7-8]，而预冷器结霜是空气中的水蒸气在低温表面直接凝华为霜的过程。

发展类SABRE 的组合式发动机，进气预冷器的结霜机理和抑霜技术是必须解决的难题，其中，强对流条件下低温表面的结霜特点和规律又是其基础。本文中将大于流速10 m/s 的流动称为强对流条件，以区别于目前大多数低速流动条件下结霜研究中的强迫对流。目前，低温表面上结霜的模拟方法可分为三类：第一类是使用基于实验经验关系式的一维模型[9-11]，但该类方法是单向的流动影响结霜，无法求解与霜层动态变化对流场和传热的影响，并且无法求解复杂外形上的结霜，主要用于平板上的结霜模拟；第二类是同时分别求解湿空气中的流场、传热传质，以及霜层中的传热传质，湿空气与霜层之间的耦合作用通过界面上的传热传质交换实现[12-15]；第三类是使用多相流方法，将霜层看作流体，使用一套方程组同时求解空气和霜层中流场和传热传质[16-20]。以上三类模型中，多相流方法不需要处理网格移动和重构问题，因此适合模拟流动、传热、传质强耦合条件下的霜层生长问题。然而，已有的结霜模拟仍集中在自然对流或低速流动条件下的结霜。

本文发展了一种新的多相流模拟方法—p-VOF 方法（pseudo-VOF），针对作为预冷换热器基本单元的圆管，开展了强对流条件下的常物性霜层二维圆管动态结霜模拟研究，分析了强对流条件下低温圆管结霜的大致规律，为预冷换热器结霜特性研究提供了基础方法。

1 动态结霜模拟算法

p-VOF 方法是一种多相流模拟伪VOF 方法。该方法是基于VOF 方法的整体架构，求解简化的质量守恒方程，替代求解CFD 软件中原有的体积分数方程。由于不解决原有的体积分数方程，所以称这种方法为伪VOF 方法。

模拟进行了以下简化和假设：1）湿空气是具有常物性的不可压缩牛顿流体；2）当霜面温度低于冰点，且湿空气中水蒸气浓度大于霜面饱和水蒸气浓度时，水蒸气在霜面凝华为霜，反之亦然；3）由于强对流条件下形成的霜层致密，可忽略霜层内部的传质；4）相变只在水蒸气和霜层（冷表面）之间的接触面上发生。

1.1 控制方程

p-VOF 方法采用两相流模型，其中湿空气是主相，霜是第二相，湿空气包含干空气和水蒸气两种组分。

1.1.1 质量守恒方程

原VOF 方法中，湿空气相和霜相两相使用相同的速度，其质量守恒方程（体积分数方程）如下：

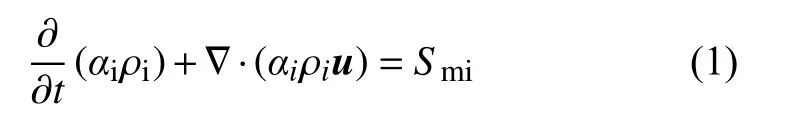
式中：α为体积分数，%；ρ为密度，kg/m3；u为速度矢量，m/s；t为时间，s；下标i代表a 或f，分别表示湿空气相或霜相；两相的体积分数之和为1。Sm是相变引起的质量源相或质量汇项，kg/(m3·s)，当i取f 时，Sm即为Smf。

由于原VOF 方法将所有物相均当作流体处理，所以每种物相均有对流项。但由于实际中的霜相是不会移动的，加之湿空气为不可压缩的假设，所以对于结霜模拟，质量守恒方程（1）中的对流项（方程左边第二项）可以忽略。因此，方程（1）可以简化为：

式中：p为压力，Pa；μ为混合物的黏性，N·s/m2；F是体积力或动量源相，N/m3。所有的变量都定义为两相混合，并且能够通过各相的体积分数权重计算出相关参数。

1.1.3 能量守恒方程

能量守恒方程也由湿空气相和霜相两相共用：

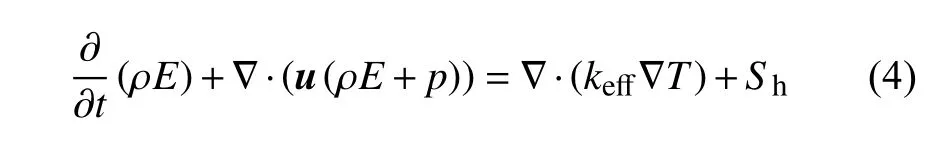
式中：E是两相混合物的内能，J/kg；keff是有效热导率，W/(m·K)；Sh是相变导致的放热或吸热，J/(m3·s)。

1.1.4 水蒸气扩散方程

湿空气相中水蒸气组分的扩散方程如下：

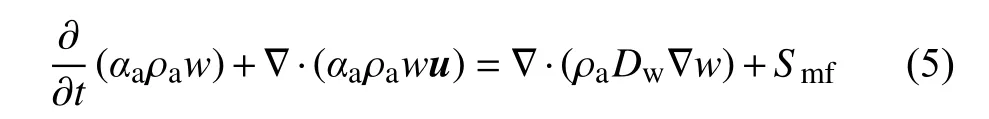
式中：w为湿空气中水蒸气的质量分数，即水蒸气含量；Dw是水蒸气扩散系数，m2/s。

1.1.5 相变质量传递速率模型

按照假设，相变只发生在霜层表面或冷板表面，发生相变的地方为相界面。在相界面处，霜相相变质量源项，也即湿空气相中水蒸气变为霜相的质量传递速率可根据动理论[21]计算得到：

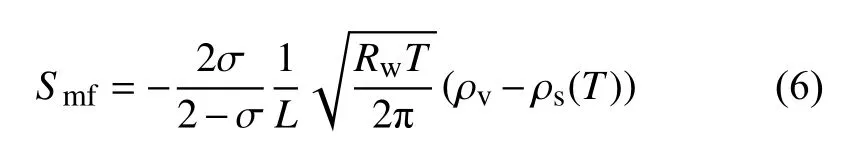
式中：ρv是相界面处水蒸气密度，kg/m3；T是相界面的温度，K；ρs是相界面处温度为T时对应的饱和水蒸气密度，kg/m3；L是网格单元特征长度，m；Rw是水蒸气气体常数，J/(kg·K)；σ是校正系数，对于水的相变一般取0.03[21]。其中，除以网格单元特征长度L的目的是将面相变速率转化为体积相变速率。

能量守恒方程（4）中的能量源项Sh为相变引起的潜热变化，在该模拟中只在相界面处为非零值：

式中：γ为相变潜热，J/kg。

1.2 解算方法

1.2.1 模拟流程

该瞬态二维结霜模拟基于FLUENT 的VOF 方法框架通过用户自定义函数（user defined function，UDF）实现。模拟的整体流程如图1 所示，图中n为已进行的时间步数，N为设定的总时间步数。

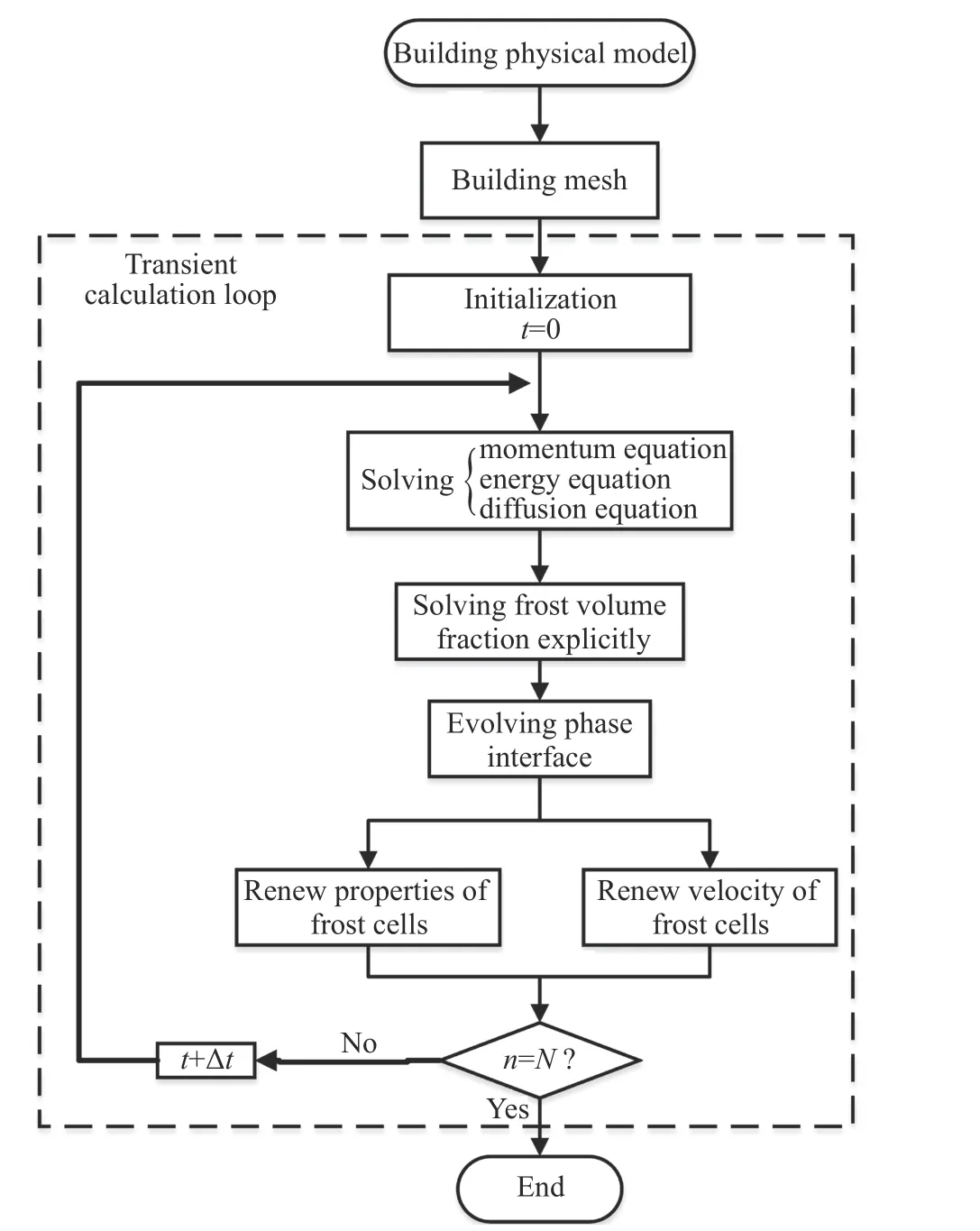
图1 结霜模拟流程图Fig. 1 Flow chart of frosting simulations

使用压力-速度耦合解算的PISO 算法，速度使用PRESTO！方法离散。动量方程和能量方程采用二阶迎风格式，水蒸气扩散方程采用一阶迎风格式。

在每个计算时间步中，可由方程（2）整理得到方程（8）。相界面上霜相的体积分数变化值，即可通过显式求解方程（8）得到：

其中，Δt是时间步长，s；Δαf是时间步长Δt内的霜相体积分数变化，%。由于显式求解方程（8），稳定计算的时间步长可提高至1 s 量级。

1.2.2 相界面判定方法

由于相变只发生在相界面，只需要对相界面上的单元格进行结霜相变计算即可。满足如下条件的网格单元则判定为相界面单元（以下ε为一个极小值，例如1×10-12）：

1）单元格中霜相的体积分数介于ε和1-ε之间；

2）单元格中霜相的体积分数小于ε，但该单元格的毗邻单元中有霜相体积分数大于1-ε的单元格；

3）单元格毗邻低温表面且霜相体积分数小于ε。

1.2.3 实现与修正方法

p-VOF 方法中霜相体积分数更新、源项计算、相界面网格单元搜索等功能均通过UDFs 实现，并关联到FLUENT 的非稳态计算过程中。为实现霜层固定不动，将霜相的黏性系数设置为一个大值（例如1×108）并将霜相的速度置零。此外，由于p-VOF 方法使用了FLUENT 的VOF 方法架构却未求解FLUENT原有的VOF 方程，热导率和黏性系数不能正确传输用于计算，因此还需要使用UDFs 对各相的热导率和黏性系数进行赋值，以得到正确的结霜模拟。

2 二维圆管动态结霜行为预测

对二维低温圆管动态结霜行为进行了模拟，并比较了各种因素的影响。本研究的主要目的是确认p-VOF方法能够用于强对流条件下低温圆管外形的结霜模拟，且能正确反映圆管外形下流动、传热与霜层形貌变化的相互耦合关系。因此，卡门涡街现象作为次要因素而暂时忽略（捕捉卡门涡街流动的时间步长需为10-6s 量级以下，时长30 min 及以上的结霜模拟也无法承受这种巨大的时间开销）。同时，鉴于圆管外形的对称性并为减小计算量，使用半圆管模型网格进行模拟，模拟所使用的网格如图2 所示，圆管半径为5 mm。对管壁附近的网格进行了加密处理，如图3所示。使用SA 湍流模型，时间步长使用1 s。模拟所使用的霜层密度为560 kg/m3、热导率为0.2 W/(m·K)。模拟状态如表1 所示。

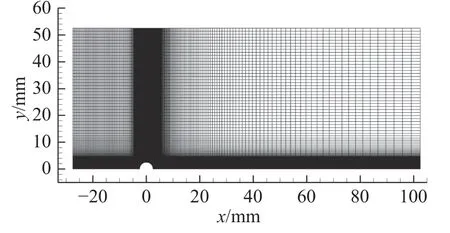
图2 结霜模拟使用的网格Fig. 2 Mesh for frosting simulations

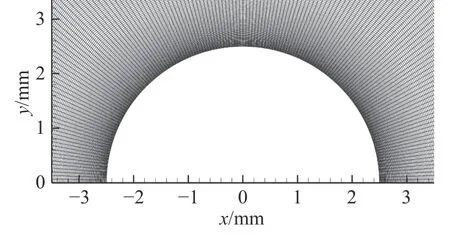
图3 管壁附近的的加密网格Fig. 3 Close-up view of the refined mesh around the tube

表1 结霜模拟状态表Table 1 Parameters for frosting simulations

2.1 低温圆管动态结霜行为

以管壁温度250 K、来流速度10 m/s、来流温度310 K 和相对湿度7%（对应水蒸气含量为0.002 7）为基准状态。二维圆管上结霜60 min 的霜层平均厚度变化情况如图4 所示（霜层平均厚度由霜层截面积除以1/2 圆管周长得到）。在结霜初期，霜层生长速率较快，随着结霜的进行，霜层生长速率逐渐变慢。结霜30 min 时的平均霜层厚度为0.77 mm，结霜60 min 时的平均厚度为0.93 mm，即后30 min 的霜层平均厚度仅增加了0.16 mm。

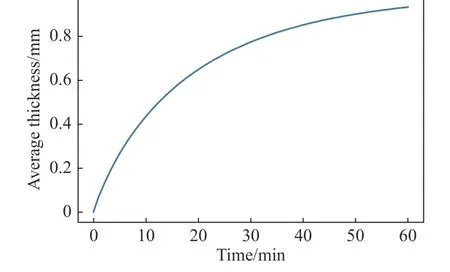
图4 圆管表面霜层平均厚度变化情况Fig. 4 Variation of the average thickness of the frost layer with time on the tube surface

霜层形貌随时间变化情况如图5 所示，来流方向为从左至右，红色区域为霜相，蓝色区域为湿空气相，黑色区域为圆管。随时间变化，圆管上的霜层形貌呈现明显的非均匀特征，反映了霜层与圆管扰流流动相互耦合作用的影响。在结霜初期，圆管前缘和后缘的结霜厚度较相近且较厚，圆管侧后方位置的霜层相对较薄。随着结霜的进行，圆管前缘和后缘的霜层厚度逐渐变大，但到20 min 以后，这两处的霜层厚度增加已不明显。然而，圆管侧后方位置的霜层一直持续生长：在结霜初期，该处的霜层最薄，在10 min 时其厚度已经和前后缘的霜层厚度基本相当，到20 min时，已高于其他位置的霜层，在60 min 时形成明显凸起。

图5 圆管表面霜层形貌随时间变化情况Fig. 5 Evolution of frost layer morphology on tube surface

图6 为不同时刻的圆管附近的速度场和温度场变化图，其中，上半部分为带流线的速度云图，下半部分为带流线的温度云图。从速度云图中可以看到，在圆管前缘位置处为流动滞止区，在圆管的侧面靠前的位置有一个高速区，气流在此位置有一定的加速。在圆管侧后方位置，开始发生流动分离，从此处位置开始在圆管后部产生明显的回流区，在回流区内的空气流速较低。随着结霜进行，霜层的增厚，圆管后部的回流区逐渐变大。从温度云图中可知，在圆管前缘的温度梯度大，后缘的温度梯度稍小，在侧后方的温度边界层呈凸出的形式，该部分的温度梯度最小，这与圆管上流动的滞止、分离和回流直接相关。

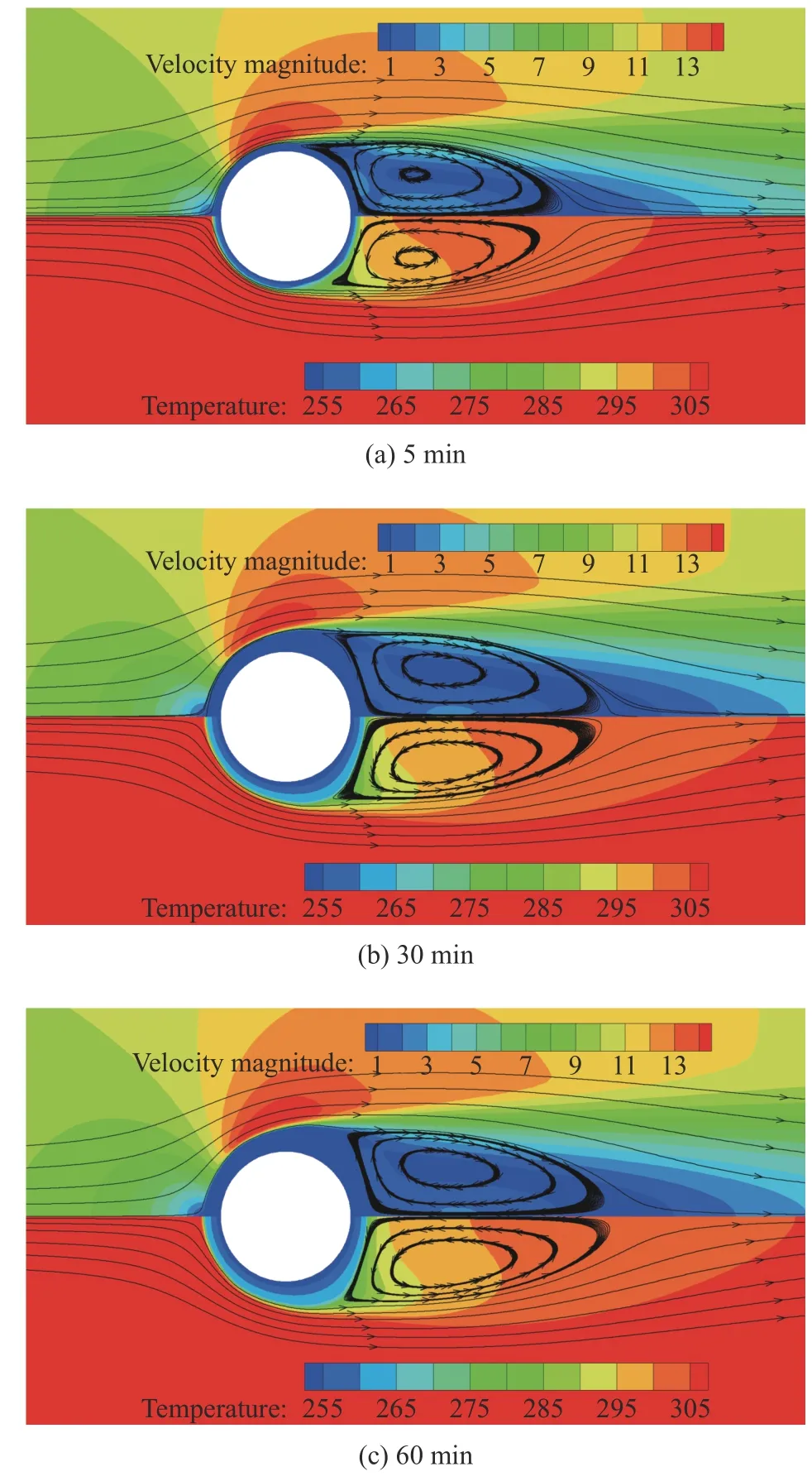
图6 圆管附近速度场（上半部分）和温度场（下半部分）随时间变化情况Fig. 6 Variations of velocity (upper) and temperature (lower)contours with time near the tube

图7 是圆管附近湿空气中水蒸气含量变化情况。该图中，圆管上的蓝色部分为霜层，霜层内的湿空气相体积分数为0，因此水蒸气含量也相应地为0。在5 min 时，圆管侧后方位置附近的水蒸气含量最低，随着结霜的进行，霜层附近的水蒸气含量逐渐升高，在60 min 时，除了霜面附近极少区域有低水蒸气含量的地方，霜层附近其他位置的水蒸气含量基本都已达到了来流水蒸气含量的0.002 7。

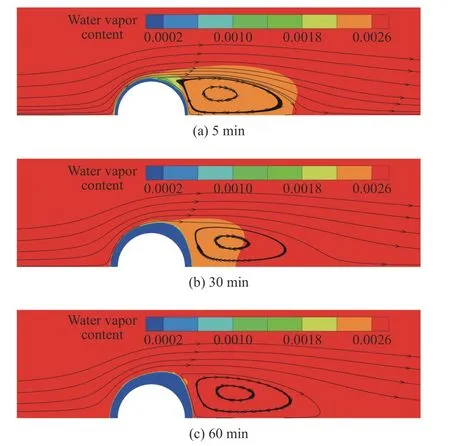
图7 圆管附近水蒸气含量随时间变化情况Fig. 7 Variation of the water vapor content with time near the tube

对比霜层形貌、温度、速度场以及水蒸气含量变化情况，圆管侧后方位置在结霜初期霜层较薄是因为此处速度梯度小、温度梯度小、水蒸气含量低，导致此处的传热较弱、水蒸气传质较慢，由此表现为侧后方位置霜层生长较慢、霜层较薄。而圆管后缘处，虽然湿空气流速较低，但是由于该处的流动方向是朝向圆管后缘的，使得该处的温度梯度和水蒸气含量相对于圆管侧后方位置更大，霜层生长速率更高，使得圆管前缘和后缘处的霜层厚度无未明显差异。

随着结霜的进行，圆管侧后方位置的霜层逐渐凸起高于其他位置的霜层。其原因是圆管侧后方位置的空气流速低且温度梯度小，虽然结霜速率小，霜层增长慢，但此处的热流密度更小、达到传热平衡时的霜层更厚。

2.2 来流速度对圆管动态结霜行为的影响

不同来流速度条件下霜层平均厚度变化如图8所示，在结霜初期，来流速度越快，霜层生长速率越大，相同时间内霜层的平均厚度越大。但是，来流速度越大，结霜速率明显减慢的时间越早，霜层的最终厚度也越薄。不同来流速度条件下霜层形貌变化情况如图9 所示，当来流速度越高，圆管上的霜层越薄，侧后方的霜层凸出越明显。

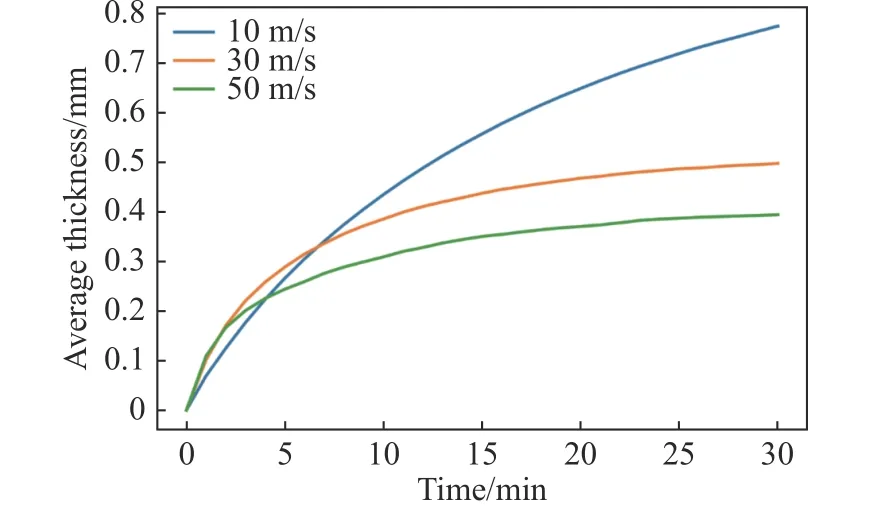
图8 不同来流速度下霜层厚度变化情况Fig. 8 Variations of the average frost layer thickness with time on the tube surface under different air velocities

图9 不同来流速度下圆管霜层形貌变化情况Fig. 9 Temporal evolutions of the frost layer morphology on the tube surface under different air velocities

不同来流速度条件下30 min 时刻的速度场和温度场情况如图10 所示，当来流速度越快，霜层越薄，是因为速度越快，对流换热量越大，达到换热平衡时，霜层热阻更小，所以霜层越薄。来流速度越快，圆管侧后方位置的温度梯度较其他位置的温度梯度相对越小，该处热流密度和传热较其他位置也相对越小。因此，来流速度越高，圆管侧后方位置的霜层凸起越相对明显。

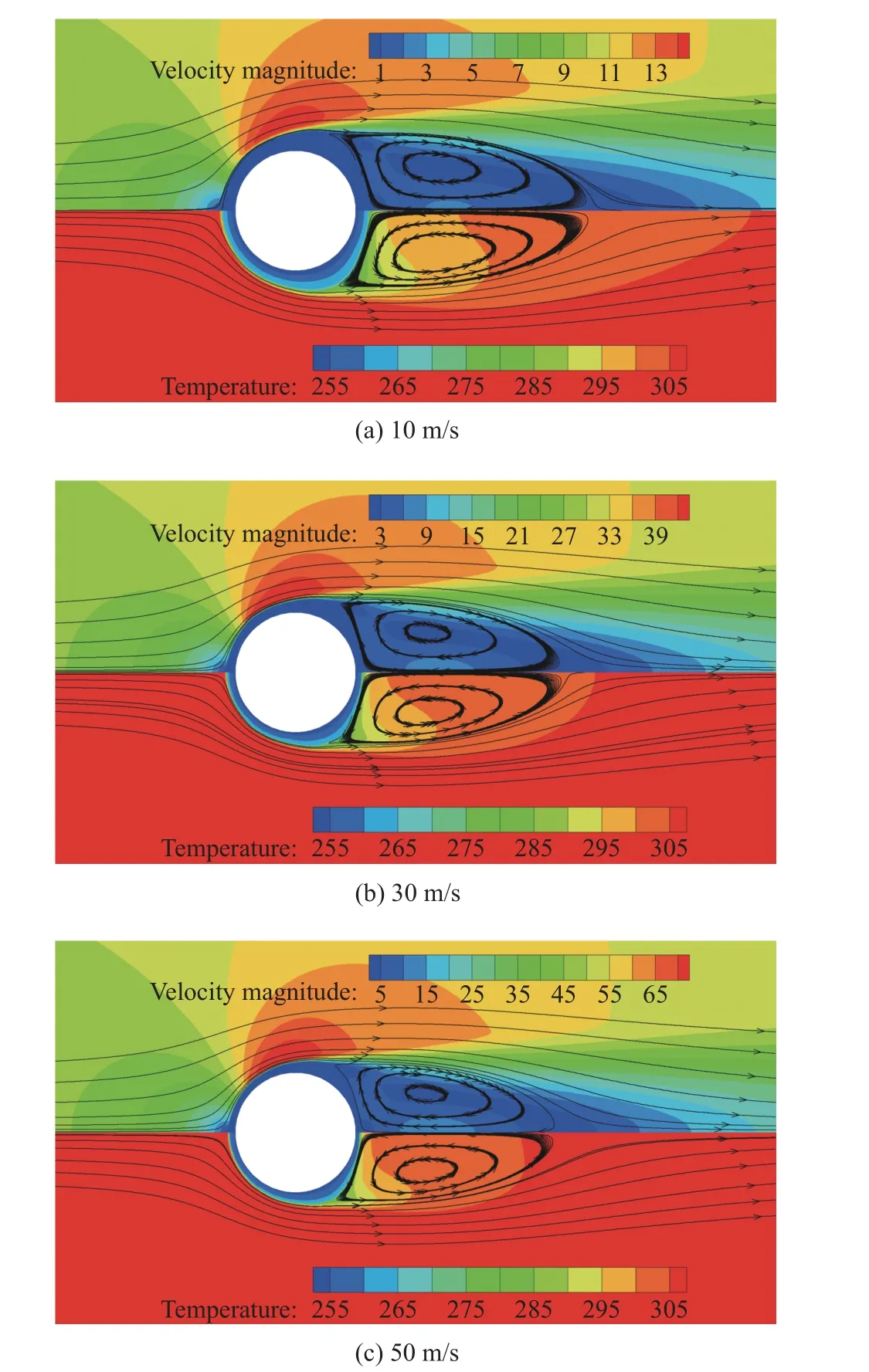
图10 不同来流速度下速度场（上半部分）与温度场（下半部分）分布情况（30 min）Fig. 10 Velocity (upper) and temperature (lower) contours under different air velocities at 30 min

2.3 来流湿度对圆管动态结霜行为的影响

不同湿度条件下的平均霜层厚度变化情况如图11 所示，相对湿度（RH）分别为5%、7%和9%。随着来流湿度的增大，霜层生长速率加快，相同时间内霜层的平均厚度越大。这是因为来流湿度越大，作为结霜驱动力的水蒸气浓度差也越大，这使得水蒸气相变速率越大，结霜速率越大，从而霜层更厚。

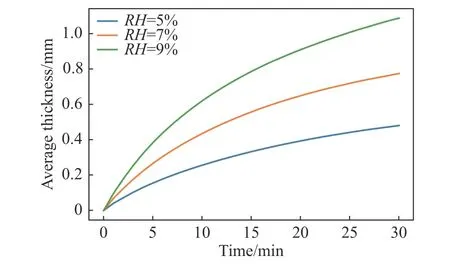
图11 不同来流湿度下平均霜层厚度变化情况Fig. 11 Variations of the average frost layer thickness with time under different air humidity

不同来流湿度条件下，霜层形貌随时间的变化情况如图12 所示。圆管上霜层的形貌，随着来流湿度的增大，呈现出圆管各处霜层均增厚的情形。这是因为来流湿度的增大，只是通过式（6）来增大结霜速率，对流动和传热没有直接影响，而这种湿度增大对结霜速率的增益，对圆管各处结霜的影响较一致。

图12 不同来流湿度下霜层形貌变化情况Fig. 12 Temporal evolution of the frost layer morphology under different air humidity

不同来流湿度条件下30 min 时刻的速度场和温度场如图13 所示，当来流湿度越大，圆管上霜层越厚，由此导致的阻挡来流的实际圆管半径越大，使得霜层后部的回流区域更大。当来流湿度越大，圆管上霜层越厚，霜层内部的温度梯度越小，但霜层外部的流场的温度分布无明显差异。

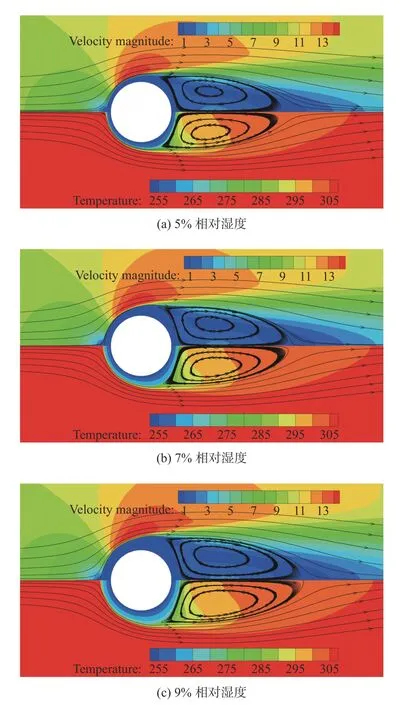
图13 不同来流湿度下速度场（上半部分）和温度场（下半部分）分布情况（30 min）Fig. 13 Velocity (upper) and temperature (lower) contours under different air humidity at 30 min

2.4 管壁温度对圆管动态结霜行为的影响

不同管壁温度的霜层平均厚度变化曲线如图14所示，圆管表面温度越低，霜层生长速率越快，相同时间内霜层的平均厚度越大。

不同管壁温度下霜层形貌变化情况如图15 所示，管壁温度越低，圆管上的霜层生长越快。管壁温度越低，在结霜初期圆管侧后方的霜层凹陷越明显，但随着结霜进行，侧后方位置的霜层均会逐渐凸起并高于其他位置的霜层厚度。在侧后方的位置会出现霜层有空隙的形貌，且管壁温度越低，这种现象越明显。发生这种现象的原因可能是，管壁温度低、结霜速率大，一旦有扰动形成小的孔隙，孔隙周围的霜层仍会迅速生长，并导致孔隙周围的水蒸气含量维持较低水平，这样孔隙处的结霜速率将更小，这就使得孔隙特征一直保持下来而不会被填满。这种现象是由于水蒸气供给能力相对较小和水蒸气凝华能力相对较强（温度相对较低）的结霜环境所导致的。这种水蒸气供给慢和相变转化（凝华）能力强的情况，与雪花或自然对流下结霜的晶枝生长的原理类似。

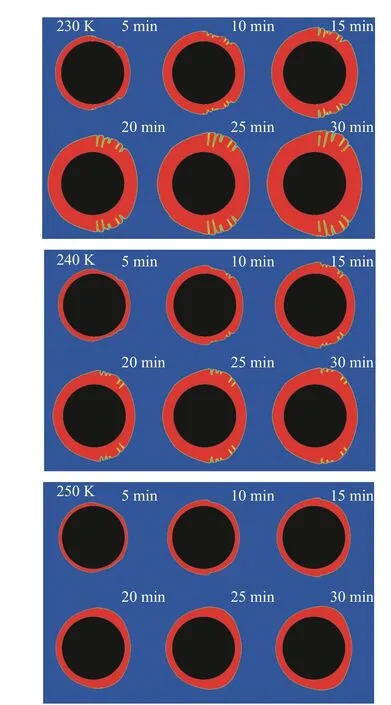
图15 不同壁面温度下圆管表面平均霜层形貌变化情况Fig. 15 Temporal evolutions of the frost layer morphology under different tube surface temperatures

不同管壁温度条件下30 min 时刻的速度场和温度场如图16 所示。从图中可看出，当管壁温度越低，霜层表面温度也越低，式（6）中霜面温度所对应的饱和水蒸气密度越低，从而水蒸气相变速率越大、结霜越快。此外，当管壁温度越低，圆管上霜层越厚，由此导致的阻挡来流的实际半径越大，使得霜层后部的回流区域越大。

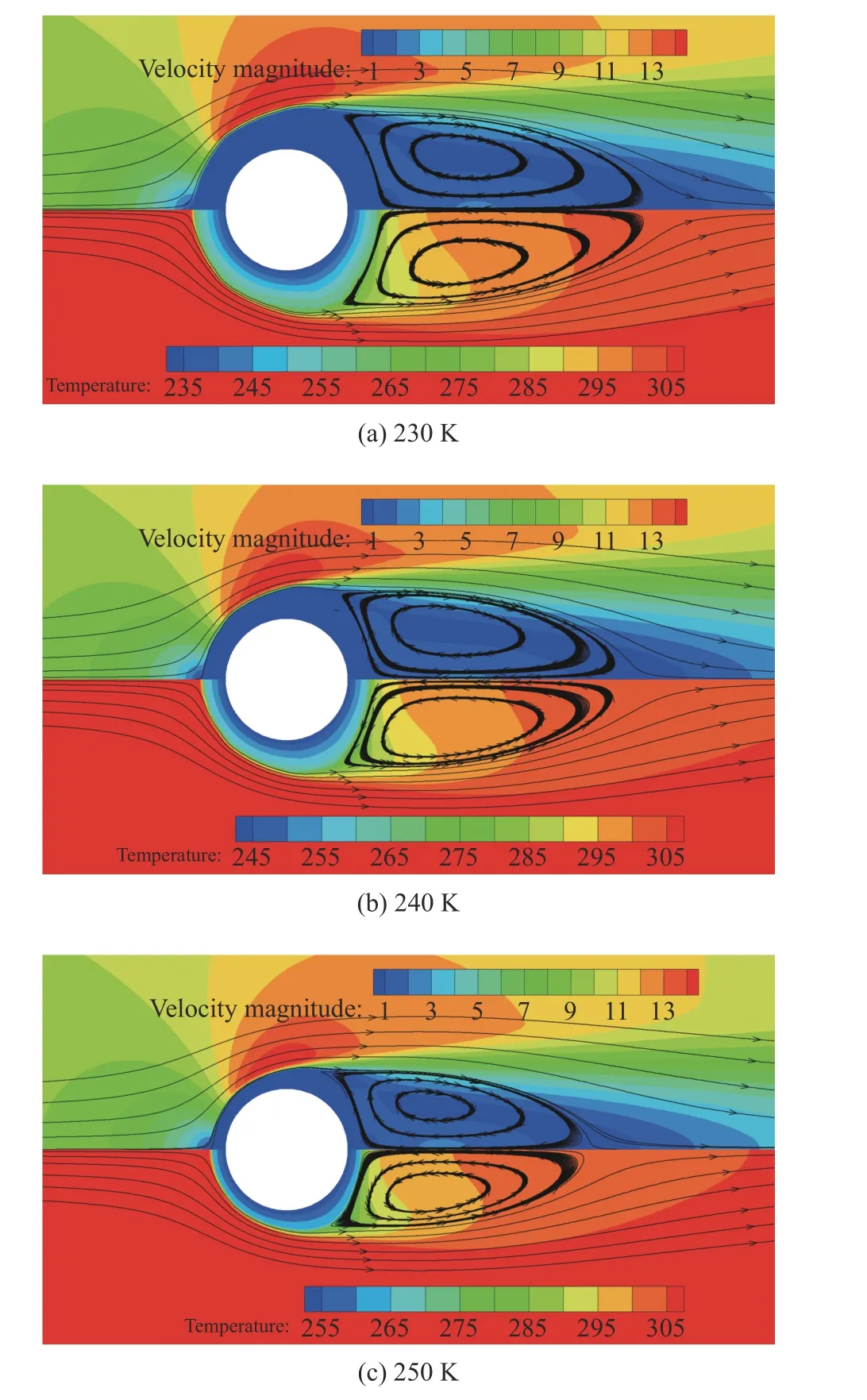
图16 不同管壁温度时的速度场(上半部分)和温度场（下半部分）分布情况（30 min）Fig. 16 Velocity (upper) and temperature (lower) contours under different tube surface temperatures at 30 min