两地中考数学试题的综合难度比较研究——以某省C市与H市为例

石玲瑜,王彦棋,谢 琼

(1.贵州师范大学 数学科学学院,贵州 贵安 新区 550025;2.怀化师范高等专科学校 小学教育学院,湖南 怀化 418000)

0 引言

中考是我国检测义务教育结果的一个重要方式,也是各所高级中学招生的重要依据,具有测评选拔的功能[1].数学作为义务教育阶段的重要学科之一,被大部分学生认为是“最让人头疼的科目”,其考试的风向必然使其成为受关注较多的一门学科,所以对中考数学试卷的研究非常必要.《义务教育数学课程标准(2011版)》提出:“合理地设计和实施书面测验有助于全面考查学生的数学学业成就,及时反馈教学成效,不断提高教学质量.”[2]而试题难度一直是研究者关注的问题,其中综合难度系数模型是研究试题难度的重要工具之一.该模型起源于美国学者Nohara提交给美国国家教育统计中心的一份工作报告,在此报告中首次提出了总体难度的概念.2002年,我国学者鲍建生在此基础上提出了数学学习评价的综合难度系数模型[3]48,随后多位研究者利用该模型对课程与试题难度进行国际比较.2013年,周九诗等以中国“人教版”和英国《数学连接》为例对中英初中数学教科书难易程度进行了比较研究[4];2014年,王建磐等选取中国、美国、法国、俄罗斯、澳大利亚的6套高中数学教材,对例题进行了难度因素的水平分析,比较了各教材中例题的难度特征,为我国高中数学教材编写提供了参考[5];2015年,邝孔秀等对中、日、韩、新、美、英、法、德、俄、澳10国有代表性的12套小学数学教科书的难度进行了定量分析,为中国小学数学教科书的编写提出了相关建议[6];2015年,卢建川等对英国数学英才选拔考试MAT的综合难度进行了分析,为中国数学英才的培育提供了借鉴[7];2018年,武小鹏等对中国与韩国高考数学试题综合难度的比较研究,为中国高考试题的命制提供了参考[8];2020年,张玉环等基于2015～2019年中国和法国高考数学试卷在综合难度视角下的比较研究,提出了关于新高考的命题建议[9].近年来,对于国内试题综合难度系数的研究也是层出不穷,但对于中考试题综合难度的研究较少,大多是对高考卷的研究,比如:张怡等基于综合难度系数模型的新高考数学试题评价研究[10];刘清等对核心素养视角下的高考试题难度进行探析[11];刘菲菲等对近5年高考数学全国卷(理科)数列试题难度的分析等[12]51.本研究在鲍建生教授的综合难度系数模型的基础上,对某省C市与H市近5年的中考试题进行对比分析,以期为各地对中考试题难度的把控提供参考.

1 研究设计

1.1 研究对象

分别选取C市与H市2017～2021年中考数学试卷作为研究对象,共10套,所有试卷的题型都只包含选择题、填空题和简答题.其中,C市2017～2019年这三年中考试题数均为26道,2020年与2021年试题数均为25道;而H市只有2019年试题数为23道,其他4个年份试题数均为24道.

1.2 研究工具

鲍建生等构建的综合难度系数模型中难度因素的水平划分如表1所示[3]49.本研究在此基础上进行了适当的修订,将“探究”这一因素改名为“认知水平”,并将水平四“探究”去掉,该因素只保留识记、理解、应用3个水平;将“背景”也只分成无背景、生活背景及科学背景3个水平;通过整理试题发现,所研究的10套试卷中涉及符号运算较少,因此“运算水平”中不考虑符号与数值运算的区别,并将“运算水平”分为无运算、简单运算及复杂运算;由于近几年对学生数学阅读能力的关注越来越多,阅读能力是学生可持续发展能力的一个重要标志[13],所以本研究增加了“阅读量”这一因素.

表1 综合难度因素的水平划分

综上所述,本研究将影响试题综合难度的因素修订为:认知水平、背景、运算水平、推理水平、知识含量及阅读量.基于中考试题的综合难度系数模型结构与内涵见表2[12]52(2页).根据表2的综合难度系数框架,建立各因素的难度系数模型

表2 基于中考试题的综合难度系数模型结构与内涵

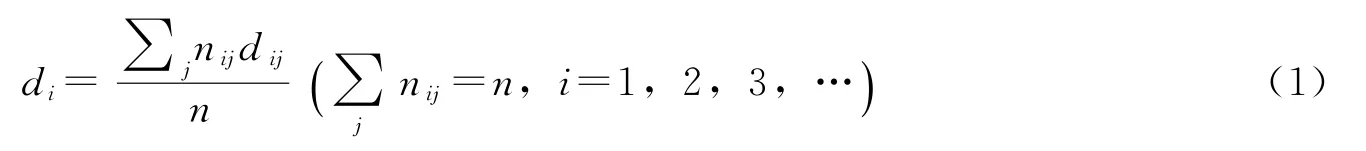
其中:d i(i=1,2,3,4,5)表示不同的维度;d ij表示第i个维度中第j个水平的权重(根据不同的水平分别取1,2,3,…);nij表示本组题目中属于第i个维度中第j个水平的题目数;n表示本组题目的总个数[3]50.

1.3 数据收集与处理

利用以上的综合难度系数模型对C市与H市共10套试卷进行分析.为方便分析,将C市的中考试卷用“C卷”表示,H市的中考试卷用“H卷”表示.下面以2道试题为例进行分析,根据6个难度因素系数的水平进行赋值.

例1(2018年C市第9题)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里、12里、13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为().

A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方干米

本题认知水平为理解、背景为科学背景、运算水平为简单运算、推理水平为一般推理、知识含量为2个知识点、阅读量为＞100个字符,其赋值情况如表3所示.

表3 例1难度因素赋值情况

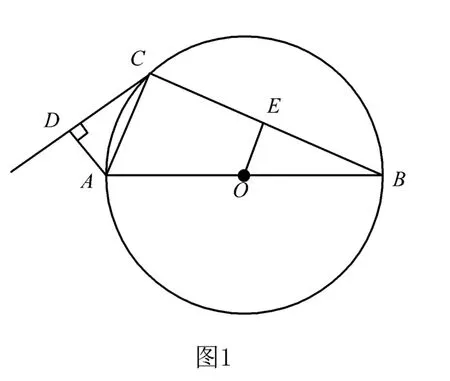
例2(2021年H市第22题)如图1,在半径为5 cm的☉O中,AB是☉O的直径,CD是过☉O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,E是BC的中点,OE=3 cm.

(1)求证:CD是☉O的切线;

(2)求AD的长.

本题有2个小问,难度因素水平按最高的水平计算,其中知识含量与阅读量为2个小问的和,本题认知水平为应用、背景为无背景、运算水平为简单运算、推理水平为一般推理、知识含量为多个知识点、阅读量为50～100个字符,其赋值情况如表4所示.

表4 例2难度因素赋值情况

按照表2中的难度系数模型结构与内涵对C市与H市中考试题进行如例1与例2的赋值,通过公式(1)计算出综合难度系数.由于篇幅有限,将最终形成的原始数据整理计算后得到表5(4页).

2 研究结果

根据表5的统计结果,下面对C市与H市2017～2021年中考数学试题在认知水平、背景、运算水平、推理水平、知识含量与阅读量6个难度因素上进行分析比较,最后通过综合难度模型雷达图对因素进行对比说明.

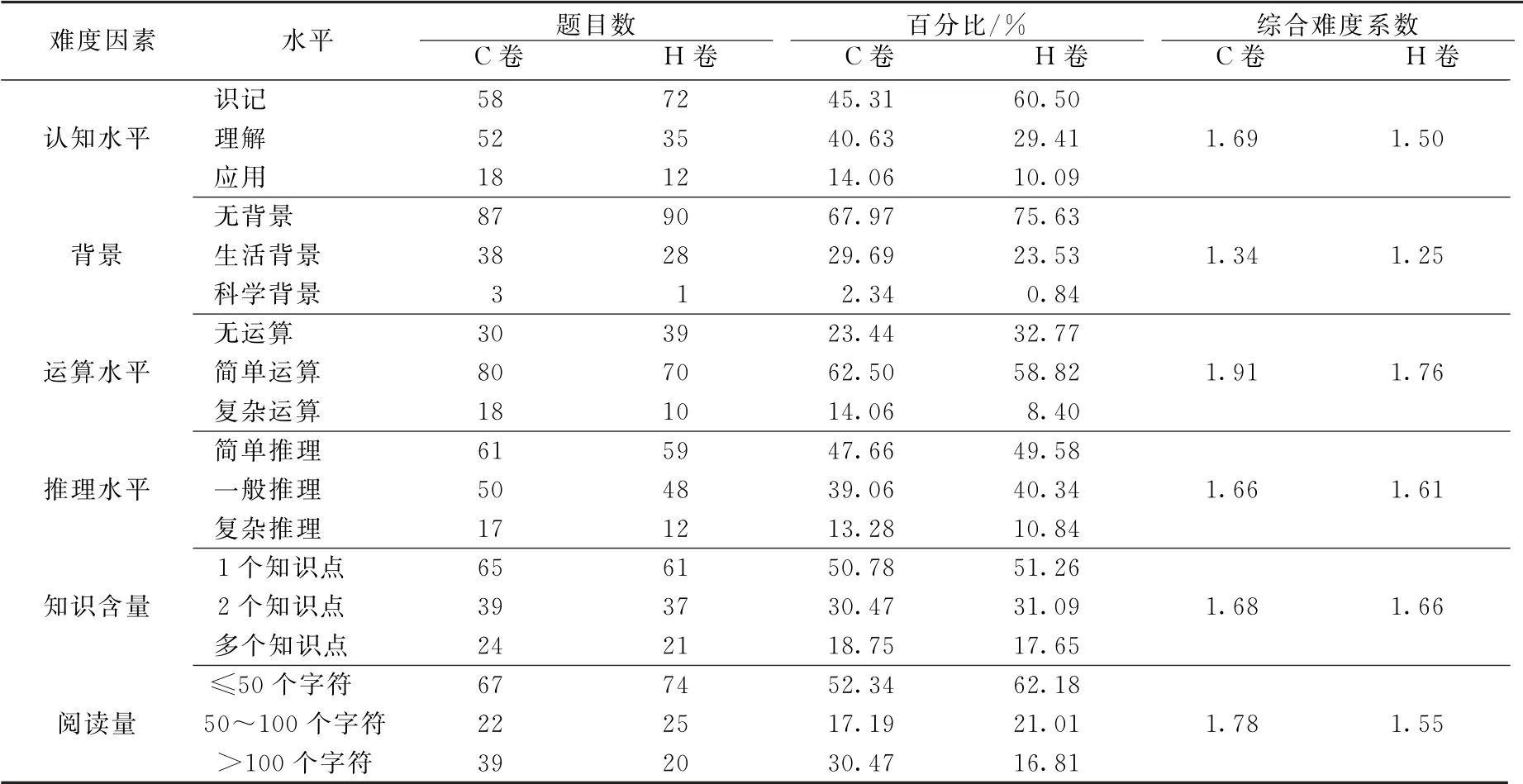
表5 2017～2021年C市与H市中考数学试题综合统计[14]

2.1 认知水平

在认知水平因素上的统计结果如图2所示.

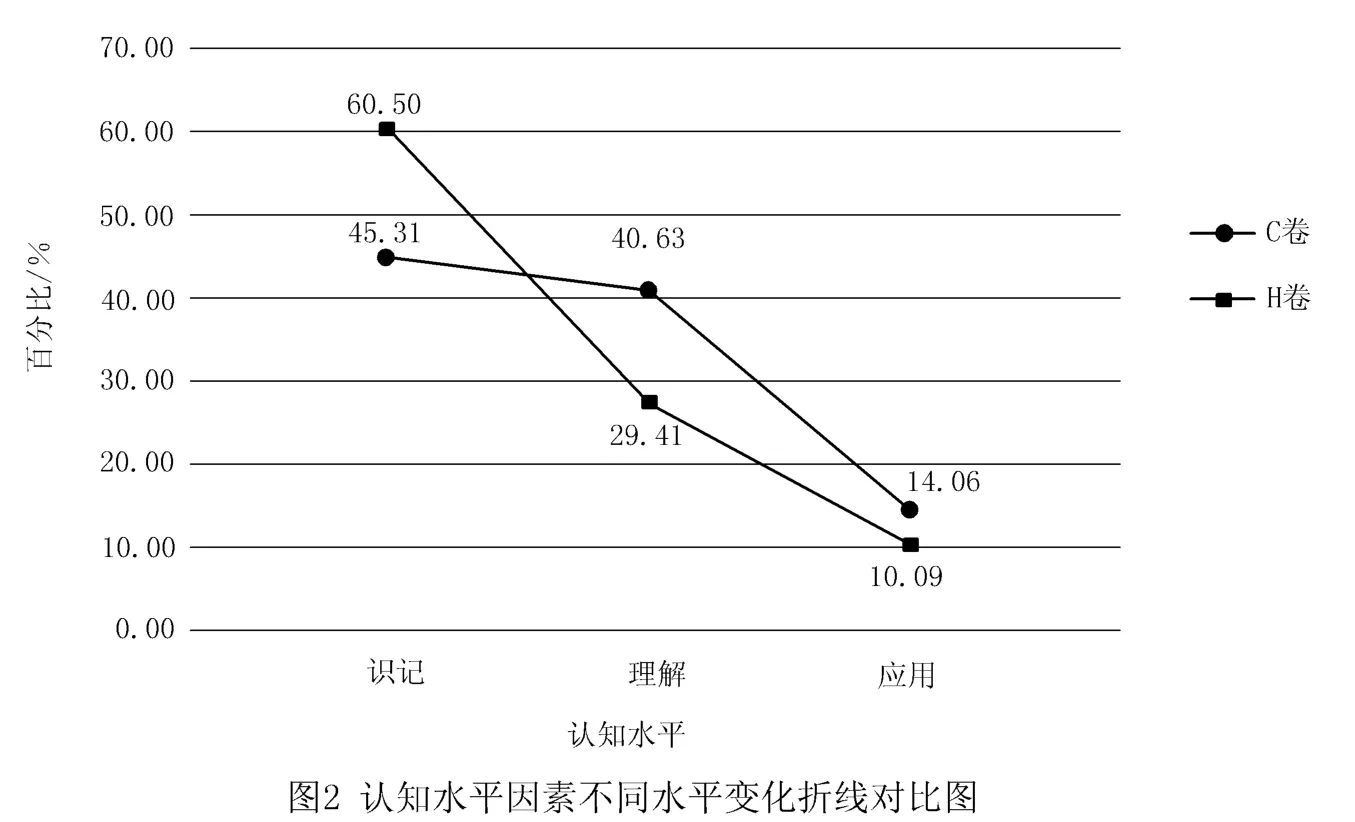
根据图2可知,2套试卷认知水平的比例随着水平层次的提高而依次递减.H卷识记水平的试题数占一半以上,而应用水平的试题数仅占总试题数的10.09%.C卷理解水平与应用水平的试题数占总试题数的54.69%,说明C卷的大部分试题需要对知识点进行理解与综合分析才能解答.C卷识记水平的试题数少于H卷,而理解水平与应用水平的试题数均多于H卷,这说明C卷重在考查对知识点的灵活运用.

2.2 背景

在背景因素上的统计结果如图3所示.

根据图3可知,H卷的无背景试题数占75.63%,科学背景试题在近5年的所有试卷中只出现了1道,仅占0.84%.C卷的无背景试题数也占据总试题数的很大一部分,有背景的试题数占32.03%,其中以生活背景为主,占29.69%.总体来看,C卷含背景的试题数要多于H卷,无论是含生活背景的试题数还是含科学背景的试题数均多于H卷.从数据统计的结果可以看出,2套试卷都重视对数学知识本身的考查,涉及背景的试题较少,尤其涉及考查科学背景的试题更是微乎其微.

2.3 运算水平

在运算水平因素上的统计结果如图4所示.

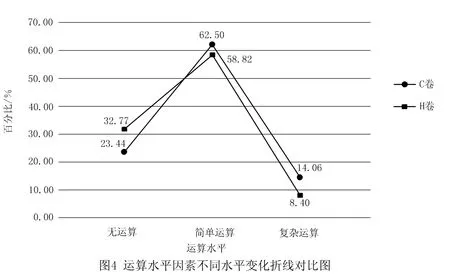
根据图4可知,H卷简单运算占58.82%,复杂运算只占8.40%,其他的试题均不需要进行运算,说明H卷对于运算能力的考查集中于简单的基础运算.C卷涉及运算的试题占76.56%,其中简单运算占62.50%,说明C卷也是重在考查学生的基本运算能力.C卷的复杂运算水平试题数约是H卷复杂运算水平试题数的2倍,而对于无运算的试题数,H卷要多于C卷,这足以说明就运算水平而言,C卷的难度明显高于H卷.

2.4 推理水平

在推理水平因素上的统计结果如图5所示.

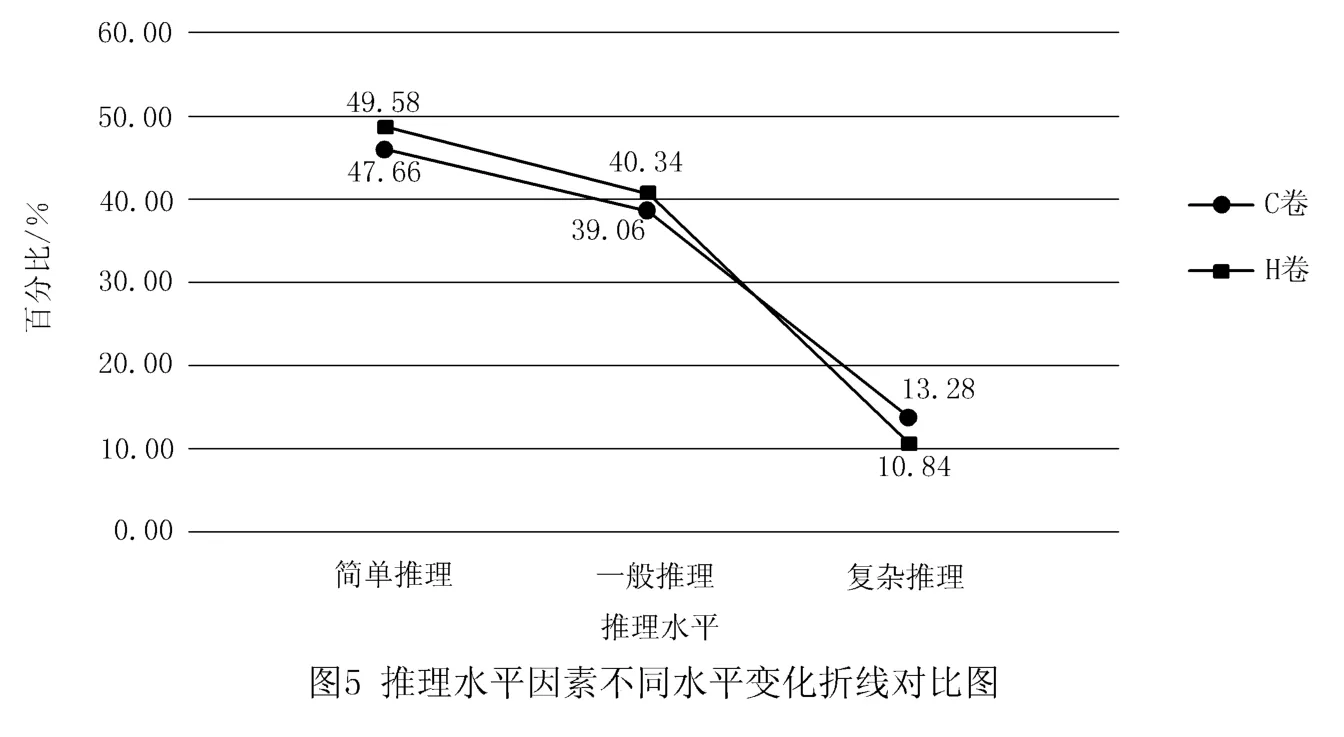
根据图5可知,2套试卷对于推理水平的考查都是随着水平的提高而依次减少,而且3个水平的考查所占比例差不多.H卷考查简单推理水平的试题数约占总试题数的一半,考查一般推理水平的试题数占40.34%,考查复杂推理水平的试题数仅占10.84%.C卷在简单推理与一般推理的考查上试题数均略少于H卷,而考查复杂推理水平的试题数占13.28%,高于H卷.总体来看,两者考查简单推理水平与一般推理水平的试题数总和都接近90%,即考查复杂推理的试题数较少,更多偏重考查学生对于基础知识的掌握情况.

2.5 知识含量

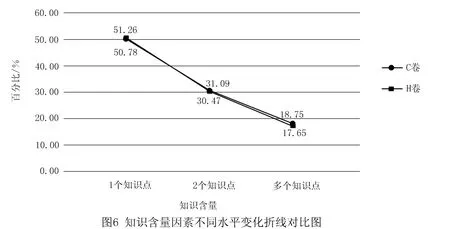
在知识含量因素上的统计结果如图6(6页)所示.

根据图6可知,两条折线几乎重合,说明H卷与C卷在知识含量的考查上区别不大,都集中在1个知识点这一水平上,占据整套试题的一半以上,对于多个知识点的考查较少.H卷在1个知识点与2个知识点水平上的试题数均略多于C卷,而在多个知识点这一水平上的试题数略少于C卷.

2.6 阅读量

在阅读量因素上的统计结果如图7所示.

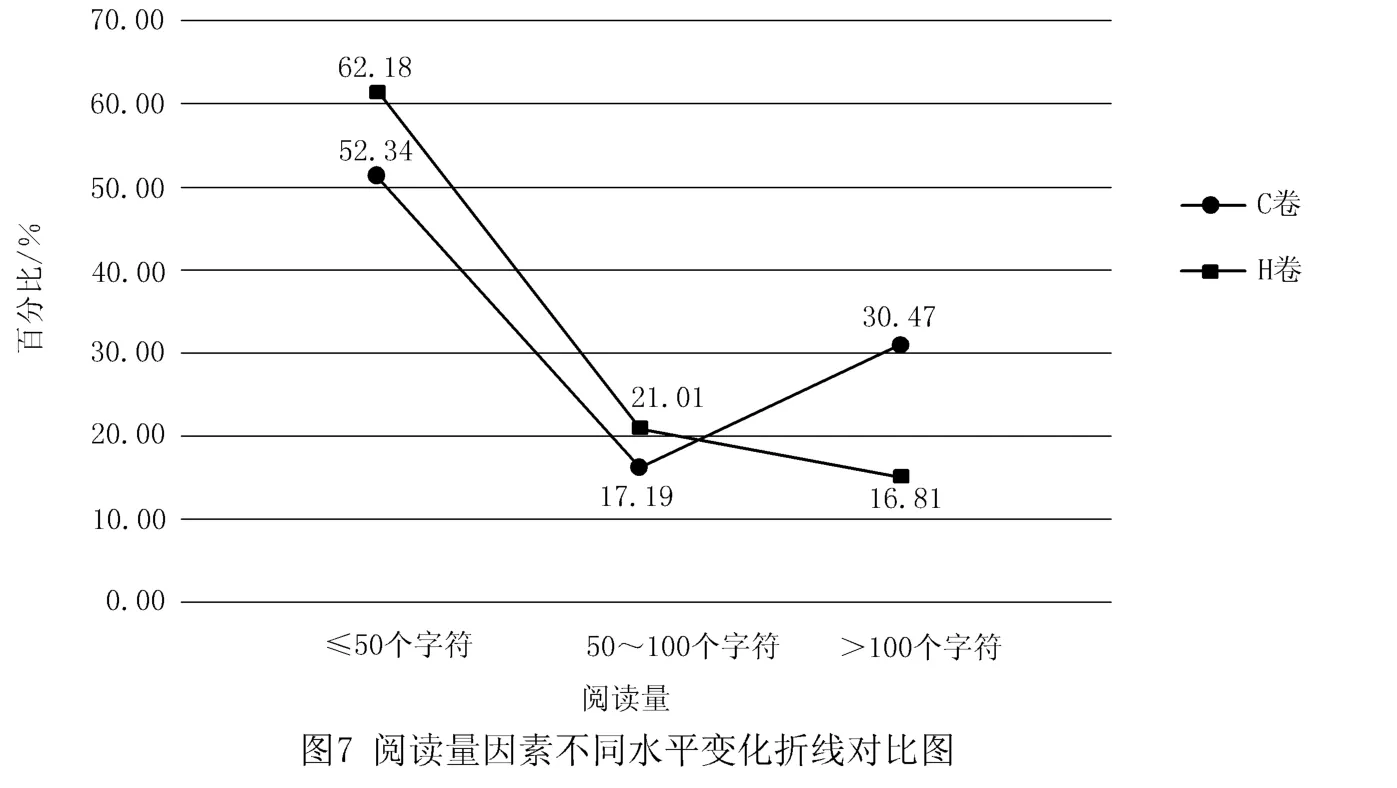
根据图7可知,H卷≤50个字符的试题数占62.18%,说明大部分试题的阅读量水平较低,＞100个字符的试题数只占16.81%.C卷≤50个字符的试题数相较于H卷少,处于第二水平的阅读量也低于H卷,而＞100个字符的试题数接近H卷 的2倍,说 明C卷的阅读量水平比H卷的阅读量水平高.总体来看,处于第二水平,即字符数在50～100个之间的试题数最少,说明2套试卷的阅读量水平均不高.

2.7 综合难度分析

表5是通过公式(1)计算出的6个难度因素各自的难度系数,根据表5中的数据得到C市与H市中考数学试题不同因素综合难度系数的雷达图,如图8所示.

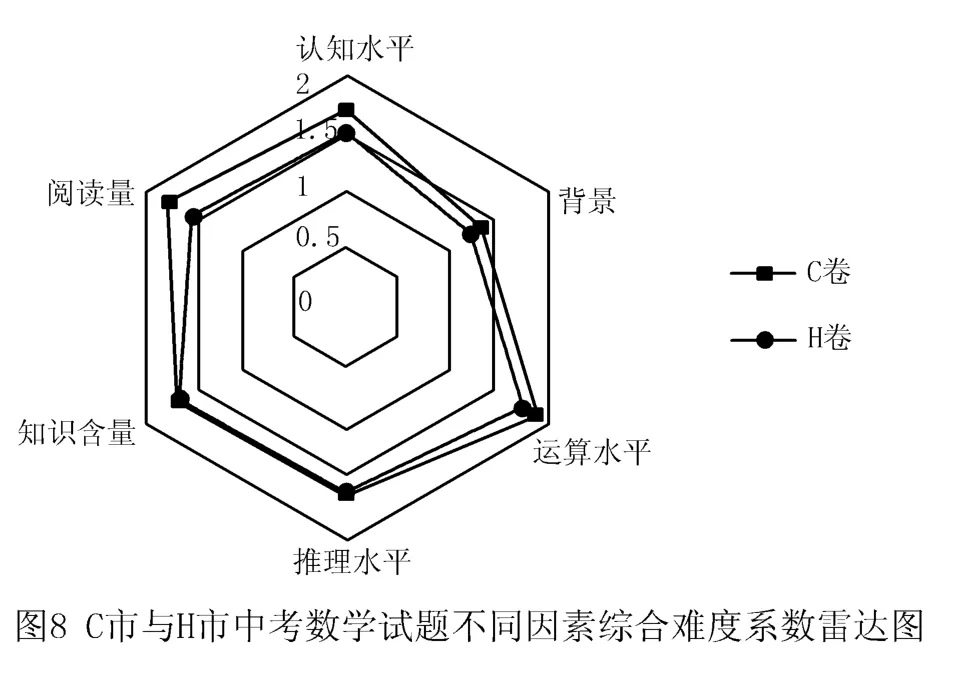
由图8可以看出,C卷与H卷在整体难度上相近,但在各难度因素上还是有差异的.在认知水平、运算水平与阅读量3个因素中,C卷的难度系数比H卷的难度系数高出大约0.2;在推理水平与知识含量2个因素中,两者之间的差异微乎其微,表现出一致性;在背景因素中,C卷的难度系数大于H卷的难度系数,说明C卷更加注重在数学试题中添加背景.由以上分析可以看出,C卷的6个难度因素系数均高于H卷,这足以说明C卷的难度大于H卷.但是,本研究只考虑了影响试题难度的6个因素,而影响试题综合难度的因素肯定不止这6个,因此这些数据仅成立于综合难度系数模型这一理论下.

3 结论与建议

3.1 研究结论

3.1.1 C卷与H卷试题在阅读量因素上有明显的差异,C卷更注重考查学生的数学阅读能力

根据图7可以看出,C卷字符数多于100个的试题数比例远远大于H卷.通过分析试卷发现,字符数较多的试题往往含有背景,仅考查纯数学知识的试题一般字符数较少.由背景因素的相关数据可以得出,C卷涉及生活背景与科学背景的试题明显多于H卷,在试题中添加背景目的就是让学生明白数学在实际生产生活中的作用,而背景的添加需要文字的描述,这就自然而然地增加了题目的阅读量.

3.1.2 H卷认知水平的难度较低,注重对学生识记水平的考查

根据表5与图2的数据统计结果可知,H卷识记水平的试题比例偏高,只要学生能记住相关概念、公式或者法则就可得出答案,不需要对相关知识点进行理解与分析;而理解水平的试题数只占识记水平试题数的一半:由此可以看出,H卷在不同认知水平的试题数不太均衡,这可能与当地的教育水平有一定的关系,H市的教育水平相对落后,出卷人也会考虑学生的实际情况.虽然杜绝在考试中出现繁难偏杂的“怪题”,但是试题过于简单,就会失去“数学味”.而C卷识记水平与理解水平的试题比例约为1∶1,可以看出C卷重在考查这2个水平.中考是由各市自主命题,如果只考虑当地学生的实际情况,那么中考过后学生面临的将是与全国各地的学生进行竞争,所以提高当地的教育质量才是关键,而不是一味地降低考试难度.

3.1.3 C卷6个因素的难度系数均高于H卷,即C卷的综合难度高于H卷

研究结果显示,C卷6个因素的难度系数都比H卷的难度系数高,这意味着C卷每一个因素的考查水平都高于H卷,即C卷难于H卷.C市属于该省的省会城市,拥有全省最好的教育资源,学生的综合水平要高于H市学生的综合水平,所以这一结果也符合当前的教育现状.尤其是认知水平、运算水平及阅读量这3个因素上,C卷明显高于H卷.从各因素不同水平变化折线对比图来看,C卷在各因素不同水平的出题比例上也优于H卷,试卷的结构更加合理.H卷在各因素不同水平的出题比例上应该有所优化,比如含有背景的题目较少,应该将实际生产生活融入到试题中.

3.2 命题建议

3.2.1 均衡各难度因素,优化试卷质量

C卷除了背景这一因素外,其他5个因素的难度相差不大,具有一定的平衡性,总体来看均衡性表现不错.但是,H卷在认知水平、背景与阅读量3个因素上的难度系数明显小于其他几个因素.在编制试题时,应该综合考虑各难度因素对试卷总体难度的影响程度,这样才能更好地凸显中考的评价与选拔功能.各地区自主命题赋予了地方更多选拔人才的权利,所以各地也应该充分考虑本地区的教育水平,了解本地区不同层次的人对中考试题的需求,同时也要学习其他地区在试题编制上的优点.目前,教育者十分重视学生数学核心素养的形成,所以考试命题要紧跟教育趋势,充分考虑各因素在核心素养形成过程中所起的不同作用,均衡各难度因素,优化试卷质量[15].

3.2.2 丰富试题背景,贴近实际生活

充分考虑初中生的年龄特点,结合其认知能力在试题中编入适当的背景,从而使他们对数学能有更好的认知.由本研究的统计数据可见,目前中考试题的编制对背景的应用有所欠缺.初中阶段所学习的数学知识绝大部分来源于生活并应用于生活,在考题中融入生活情境可以让学生更加深刻地体会这一点.本研究将科学背景的内涵定义为以数学文化为背景或涉及其他学科.2套试卷中涉及科学背景的试题极少,说明这两个地区对于数学文化的教学不够重视,或者在考题编制时忽视了数学文化的渗透;没有凸显学科之间的联系,在中考命题中融入其他学科的相关内容,会使学生了解到各学科之间是相互关联的.只有将数学知识的考查添加适当的背景,在日常教学过程中教师才会更加注重将数学与实际生产生活联系起来,从而激发学生学习数学的兴趣.

3.2.3 创新题型设置,培养思维能力

通过对两个地区近5年中考试题的分析发现,试题的类型都是“循规蹈矩”,具有创新性的试题少之又少.国家大力提倡培养创新型人才,而创新能力是需要通过教育去培养的,如果我们用来评价学生学习效果的试题都是几十年如一日,在题型和内容上没有新的突破,表现出千篇一律的风格,那么学生的思维能力又如何能得到提高.近几年,还是有一部分教育研究者意识到了这一点,总体趋势在向着好的方向发展,很多地方的中考试卷出现了开放性的试题,包括一些游戏与活动等,这些元素的融入可以活跃学生的思维.

3.3 研究不足

综合难度系数的影响因素很多且较为复杂,除了本研究中所提到的6个因素,吕世虎等人还提出了试题量、试题难度分布、试卷新颖性等因素[16],所以本研究存在一定的局限性,还有待进一步的完善.在各难度因素水平的确定过程中,会存在一定的主观性,这会导致研究结果存在误差,但对研究结果的影响不大.