统计分析理论在大学生学习成绩分析中的应用
2022-11-09江志冬
江志冬
(福州大学至诚学院经济管理系,福建 福州 350002)
0 引言
现阶段,各高等院校正着力推进本科教育内涵式发展[1],本科生培养质量是教育部门、高等院校关注的重点.大学生的学习成绩是检验课程学习成果的重要指标,作为高等院校的教务部门不能仅仅关注学习成绩的及格率,更应该分析隐藏在这些成绩背后的现象,为提高教学质量奠定基础.何韵竹等采用数据挖掘算法分析了大学生成绩,研究发现计算机网络、操作系统及英语是影响软件工程专业学生能否获得奖学金的重要科目[2];黄蕙等采用关联规则方法研究学生成绩,建议教务管理部门根据关联规则分析结果调整排课顺序,提升教学效率[3];贾连广等采用相关性检验发现线性代数成绩与高等数学成绩具有很强的相关性,建议对线性代数成绩不高的学生应多加指导,以便更好地学习高等数学[4].此外,大学生成绩分析的常用方法还有决策树算法、聚类方法、回归分析方法、主成分分析方法等.
通过以上分析可知,许多学者正尝试用统计学理论、数据挖掘技术、机器学习方法等研究大学生成绩,并取得了良好成果.大部分教务管理人员采用Excel对成绩进行分析,但计算步骤较为繁琐;而如果采用数据挖掘技术、机器学习方法,则要求教务管理人员掌握数据分析技术.基于此,本文结合成绩分析的总体思路,采用常用的统计分析方法对学生学习成绩进行分析,并以某学院A专业学生学习成绩为例进行实证研究.
1 学习成绩分析思路
首先,确定分析对象并导出学习成绩,必要时对数据进行清洗,确保分析数据的准确性;其次,采用描述统计方法对成绩进行描述统计分析,计算课程成绩的及格率,对于成绩及格率较低的课程,考查其成绩结构分布情况;再次,采用差异分析方法研究成绩在性别、班级等方面的差异,采用相关性分析方法研究课程成绩的相关性;最后,根据成绩分析结果提出教学优化措施.
2 统计分析方法
本文采用的统计分析方法有两独立样本T检验、单因素方差分析、Mann-Whitney U检验、多独立样本Kruskal-Wallis检验和皮尔逊相关性分析.
(1)两独立样本T检验.该方法利用来自两个独立总体的样本推断两个总体的均值是否存在显著性差异,使用的前提是两个样本相互独立,并且样本来自的总体应服从或者近似服从正态分布.
(2)单因素方差分析.该方法用于检验两个以上总体的均值是否相等,要求数据服从或者近似服从正态分布.当总体存在差异时,可采用多重比较技术分析各组之间的均值是否存在显著性差异.
(3)Mann-Whitney U检验.该方法是一种双独立样本的非参数检验方法,两组的观测值被合并,而后赋予秩,如果秩和检验的差值较大,可认为两个样本来自不同分布[5].
(4)多独立样本Kruskal-Wallis检验.该方法用于检验多个(两个以上)总体的分布是否存在显著差异,是一种非参数统计方法,适用于数据呈非正态分布的情况[6].
(5)皮尔逊相关性分析.皮尔逊相关系数可用于度量两个变量之间线性相关性的密切程度及方向.如果计算得到的P值小于给定显著水平a(一般默认为0.05),表明变量之间存在显著的线性相关关系,否则认为变量之间不存在显著的线性相关关系.
3 实证分析
3.1 数据来源
以某学院A专业148名学生学习成绩作为数据来源.该学院为地方普通本科高校,A专业的人才培养目标为基础扎实、适应面宽、应用能力强的高级应用型人才.分析数据为A专业某个年级大一学年通过正常考试获得的成绩(不包含补考、重修).
3.2 结果与分析
3.2.1 课程成绩描述统计分析
对各门课程成绩进行描述统计分析,整理结果如表1所示.军事训练是大一新生的必修课程,通过该门课程则成绩记为60分;体育成绩包含早晨、晚上的体育锻炼成绩,如未通过规定 测 试则记0分.结合极差、标准差统计量可发现学生成绩差异较大,高数是及格率最低的科目.
3.2.2 及格率较低科目成绩结构分析
高数(上)的及格率为84.82%,高数(下)的及格率只有67.86%,说明下降幅度较大.究其原因,是由于高数(下)是高数(上)的延续,难度系数会有所增加,对于高数(上)没通过的学生而言,学习难度更是会剧增;而且,平均成绩排名靠前的学生也出现了高数(下)不及格的情况,如某学生上学期平均分位列第12名(位列年级前10.7%),但却出现高数(下)不及格的现象.通过进一步分析还发现,高分段人数较少,主要集中在60~70分;从分布结果上看,数据呈负偏态分布,说明学生成绩受到试卷结构的影响.
线性代数的及格率为75%,高分段学生的人数较为正常,但低分段学生的人数偏多.通过进一步分析发现,学生学习水平的差异很大.
3.2.3 成绩在不同维度的差异分析
学生某一学期各门课程的平均分是衡量该学生学业水平的重要指标,其计算以课程的学分为权重.从及格率的分析可以看出,大学英语(上)、计算机(上)、高数(上)、高数(下)、线性代数、微观经济学、大学英语(下)和计算机(下)的及格率具有较大的提升空间,因此以下重点分析这8门课程的平均分在性别、班级维度上的差异.在进行差异分析前,采用单样本K-S检验方法判断8门课程的成绩是否服从正态分布.经过检验发现,当显著性水平为0.05时,计算机(上)、线性代数、大一上平均分、大一下平均分近似服从正态分布,其余成绩均不服从正态分布.
3.2.3.1 成绩在性别维度上的差异分析
对服从正态分布的成绩采用两独立样本T检验,对不服从正态分布的成绩采用Mann-Whitney U检验,分析成绩在性别维度上是否存在差异.
两独立样本T检验结果见表2.从表2可以看出,当显著性水平为0.05时,可认为计算机(上)成绩在性别维度上不存在显著性差异;女生线性代数成绩显著高于男生;大一上平均分女生显著高于男生,但是大一下平均分在性别上不存在显著性差异.

表2 两独立样本T检验结果
表3显示的是Mann-Whitney U检验结果,采用中位数度量不服从正态分布的成绩水平.由表3可见,在显著性水平为0.05时,可认为女生的大学英语(上)成绩显著高于男生,其他成绩不存在显著性差异.
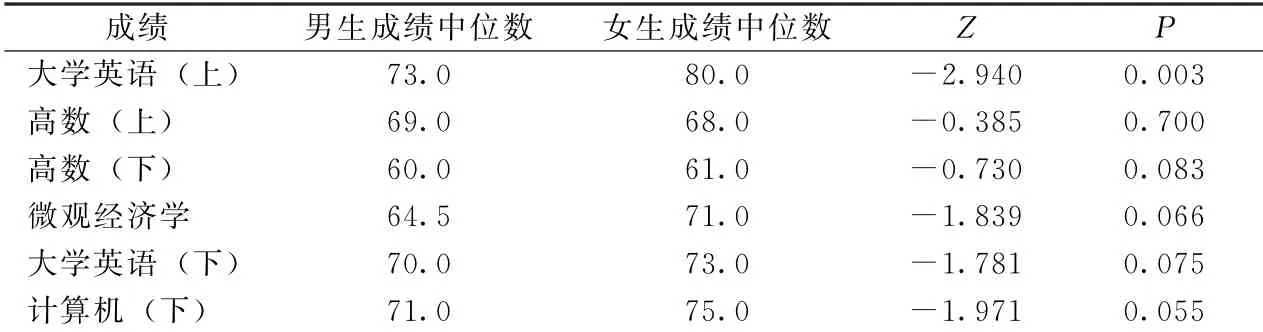
表3 Mann-Whitney U检验结果
3.2.3.2 成绩在班级维度上的差异分析
本次分析的A专业有3个班级,因此对服从正态分布的成绩采用单因素方差分析,对不服从正态分布的成绩采用多独立样本Kruskal-Wallis检验,分析成绩在班级维度上是否存在差异.
单因素方差分析结果如表4(12页)所示.由表4可见,当显著性水平为0.05时,可认为计算机(上)成绩、线性代数成绩在不同班级不存在显著性差异;大一上平均分、大一下平均分在不同班级存在显著性差异.进一步采用多重比较技术可以发现,1班大一上平均分、大一下平均分显著高于其他两个班级.

表4 单因素方差分析结果
表5显示的是多独立样本Kruskal-Wallis检验结果.由表5可见,当显著性水平为0.05时,可认为高数(上)成绩在班级维度上存在显著性差异,采用中位数度量成绩水平可发现,1班的高数(上)成绩显著高于2班、3班,其他成绩在班级维度上不存在显著性差异.
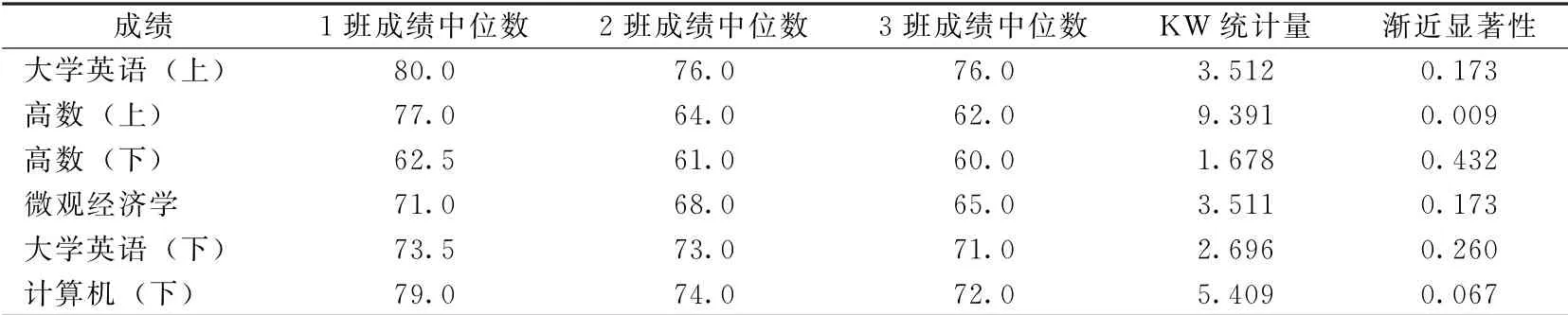
表5 Kruskal-Wallis检验结果
所选取的A专业3个班级中,学生的划分是随机的,而且3个班级的学生高考成绩没有显著差异.经过一学年的学习,总体来看,1班的成绩优于其他两个班级.根据后续的调查及座谈发现,1班的班委更为团结,注重加强班级学风建设,学习氛围良好,这也是影响班级总体成绩的重要因素.
3.2.4 课程成绩的相关性分析
采用皮尔逊相关性分析研究高数(上)成绩与高数(下)成绩和线性代数成绩的相关性,课程间的相关性分析结果如表6所示.由表6可见,当显著性水平为0.05时,可认为高数(上)成绩与高数(下)成绩、线性代数成绩存在显著正线性相关关系.因此,对高数(上)不及格或者分数较低的学生要加强辅导,从而有利于学生学好高数(下)和线性代数课程.

表6 课程间的相关性分析
4 结论
利用常用的统计分析方法对某学院A专业学生的学习成绩进行实证研究,得到以下研究结果:(1)数学类课程的及格率偏低;(2)部分课程成绩在性别维度上存在显著性差异,班级学习氛围是影响学习成绩的重要因素;(3)从相关性分析角度看,高数(上)成绩与高数(下)成绩、线性代数成绩存在显著正线性相关关系.可见,采用统计分析方法能够识别成绩分布情况,分析成绩在性别、班级维度上的差异,以及测算课程成绩的相关关系.
基于以上分析结果,该专业教学活动可从以下方面进行优化:(1)提高学生对数学类课程的学习兴趣,可从多方面、多角度展示数学的重要性,培养学生数学思维,同时开展多样化的辅导活动,加强对数学底子较弱学生的辅导;(2)营造良好的班级学习气氛,建立定期查课制度、随堂听课制度、学风督查通报制度,促使学生养成自主学习的良好习惯,以利于提升学习成绩;(3)重视数学类前置课程的学习,专业负责人应向学生阐述前置课程与后置课程之间的内在关系,引导学生重视前置课程的学习,要重点关注前置课程挂科的学生.
本文尝试采用统计分析方法对大学生成绩进行分析,为大学生成绩分析提供了可借鉴的路径.下一步,可增加成绩样本量,如分析多届学生同一门课程学习成绩的差异,分析学生在参加社团活动、担任班干部等情况下学习成绩的差异,从而拓展统计分析理论在大学生成绩分析领域的应用范围.
