利用PSS4B和GPSS附加阻尼控制抑制云南电网超低频振荡的对比分析
2022-11-09黄伟刘蔚黄润江出阳张杰
黄伟,刘蔚,黄润,江出阳,张杰
(1. 南方电网云南电力调度控制中心,云南 昆明 650011;2. 南方电网科学研究院有限责任公司,广东 广州 510663)
云南电网与南方电网主网异步联网运行后出现了长时间、大幅度的超低频振荡现象,严重危害了云南电网的安全稳定运行。经过初步研究认定,此次超低频振荡是由电网中的水电机组调速系统向系统提供了负阻尼导致,并采取了抑制措施[1-2]。
国内外学者针对水电机组引起的超低频振荡问题开展了机理研究和模型仿真等工作[3-9],研究表明:对于水电占比较大的电网,水电机组存在的水锤效应在调速器PID参数设置不合理时会恶化系统阻尼,引发超低频振荡。
国内外学者同时开展了超低频振荡的抑制措施研究,抑制措施主要分为2类。
第1类是直接优化水电机组调速器PID参数,例如:文献[9]采用极点配置法和临界参数法来优化调速器控制系统的参数,以达到抑制超低频振荡的目的;文献[10]提出考虑鲁棒稳定约束下最大化跟踪性能的调速器参数频域优化方法,可以同时满足多个方式的稳定需求,且可同时对多个机组调速器进行优化;文献[11]通过计算超低频振荡的特征根灵敏度,对调速系统参数进行优化,增大了超低频振荡模式的阻尼比;文献[12]利用矩阵扰动理论验证了统一频率模型的适用性,并提出基于结构奇异值理论的水轮机调速器参数设计方法;文献[13]提出了一种调速器参数优化方法,约束是原动机在整个振荡频率范围内的阻尼转矩,目标是原动机在不同载荷下阶跃响应综合的时间乘以误差绝对值积分(integral time multiplied absolute error,ITAE)指数,优化的参数可以保证系统在不同条件下的稳定性;文献[14]提出基于启发式方法的调速器PID参数多机协调优化策略,用于云南电网主力机组调速器PID优化;文献[15]研究了不同负荷和工作水头下原动机相频特性变化规律,基于保守工况下的原动机简化模型对调速参数开展优化整定。优化调速器PID参数虽然可以有效抑制超低频振荡,但同时也会削弱水电机组的一次调频特性,直接影响电网的频率特性和对水电机组一次调频的考核[16-17]。
第2类是通过基于附加阻尼控制的方式来抑制超低频振荡。采用的附加阻尼控制方式主要有2种:①利用电力系统稳定器(power system stabilizer,PSS)作为附加阻尼控制手段;②利用调速器侧电力系统稳定器 (governor PSS,GPSS)作为附加阻尼控制手段。其中前者加装在机组励磁系统的附加阻尼控制,后者加装在机组调速器的附加阻尼控制。文献[18]分析了PSS影响超低频振荡的机理,认为当负荷具有电压调节效应时,励磁系统通过影响负荷电压来影响负荷功率,进而影响超低频振荡;文献[19]基于复转矩系数法分析超低频振荡机理,推导出附加阻尼控制的可行性,构建了一种抑制超低频振荡的PSS控制结构,提出计及系统工况变化的控制参数鲁棒整定算法;文献[20]提出一种多机系统中同时考虑低频振荡和频率振荡的PSS优化方法;文献[21]研究了在汽轮发电机组调速器侧加入GPSS,产生正阻尼力矩,抑制低频振荡的方法;文献[22]针对云南水电机组研究和设计了一种调速器附加阻尼控制器结构,用于抑制超低频振荡;文献[23]基于含PID 型调速器的多机系统线性化状态空间模型求解超低频振荡模式,用阻尼转矩法分析调速器控制系统阻尼特性,提出一种基于相位补偿原理的GPSS抑制超低频振荡的设计方法。
目前云南电网通过优化水电机组调速器PID参数的方式来抑制超低频振荡,实际运行中出现了频率较频繁波动、稳定性变差的情况。基于附加阻尼控制方法可以协调抑制超低频振荡和一次调频性能,是可选技术方案。PSS和GPSS附加阻尼控制方式在理论和机理上都可以抑制超低频振荡,但对2种方式的特点和效果还缺少进一步对比研究。
本文主要针对云南电网超低频振荡问题,结合云南水电机组实际参数,对比分析PSS4B型的PSS和GPSS附加阻尼控制用于抑制超低频振荡时的特点和效果等。首先建立基于单机带负荷无穷大系统的小干扰分析模型,然后以云南电网某大型水电机组为算例,分析机组低频振荡和超低频振荡模式间的同源关系,并通过特征根轨迹对比分析PSS4B和GPSS附加阻尼控制用于抑制超低频振荡时的特点和效果差异。
1 PSS4B和GPSS简介
1.1 PSS4B简介[24]
PSS是抑制电力系统低频振荡的一种重要手段,目前常用的是PSS2B型为代表的单频段PSS。
2000年加拿大魁北克电力局提出了PSS4B型多频段PSS。PSS4B的特点在于将转速/功率信号分为低频(0.01~0.1 Hz)、中频(0.1~1 Hz)及高频(1~10 Hz)3个频段,并通过3个可以单独调节增益、相位、输出限幅及滤波器参数的通道进行调节,从而可以分别为高、中、低3个频段提供合适的阻尼。
PSS4B解决了PSS2B存在的一些不足,包括:①在中低频段采用转速信号,经过低通滤波处理,解决了高频段转速测量精度问题;在高频段采用有功功率信号,解决了无功“反调”问题。②采用差分滤波和超前滞后结合的方式,解决了PSS2B中只有超前滞后环节而导致的增益单调性问题,提高了中、低频段的增益。
1.2 GPSS简介
GPSS作为附加阻尼控制手段,其输入信号为转速或功率偏差的1种或几种信号组合,其控制目标是:当出现超低频振荡时,能产生与发电机转速偏差Δω反向的机械功率(力矩)增量ΔTm,为系统增加正的机械阻尼。GPSS改变机组原动机的输入功率,而不参与电磁功率改变。
GPSS模型中的斜坡跟踪函数以及二级隔直环节的作用是对超低频段进行带通滤波和隔直。GPSS输出信号一般叠加到开度指令信号上。GPSS模型如图1所示[21]。图1中:Δω为发电机转速偏差,m、n、T8和T9为轴系扭振滤波环节的参数,Tw1和Tw2分别为2个隔直环节的时间常数,T1和T2、T3和T4、T5和T6分别为3个超前滞后环节的时间常数,KGP为放大倍数,YGPmax、YGPmin分别为输出YGP的上、下限幅值,s为微分算子。

图1 GPSS模型
接入GPSS的水电机组调速系统的模型如图2所示,图2中:Kp、Ki和Kd为调速器的PID参数,bp为调差系数,Ty为伺服环节时间常数,Tw为水锤效应时间常数,ΔTm为机械功率输出变化量。

图2 带GPSS的水轮发电机调速系统传递函数
2 单机带负荷无穷大系统建模
考虑到分析电网低频振荡问题时一般采用基于考虑励磁系统和PSS的单机无穷大系统模型[25],对于云南电网这种典型的水电占比较大(约占85%)的电网,分析调速系统引起的超低频振荡问题时一般采用基于考虑调速系统的单机带负荷系统模型[1-15]。
本文通过建立单机带负荷无穷大系统模型,建立单机无穷大系统和单机带负荷系统之间的联系,以方便分析低频振荡和超低频振荡模式之间的联系,以及比较PSS和GPSS抑制超低频振荡的效果。
2.1 单机带负荷无穷大系统模型
单机带负荷接入无穷大系统模型如图3所示。

图3 单机带负荷无穷大系统

(1)
(2)
式(1)、(2)中:PL0、QL0、UL0分别为工作点稳态运行时负荷母线的有功功率、无功功率和电压幅值;系数ap、bp、cp和aq、bq、cq与负荷组成有关,且满足ap+bp+cp=1,aq+bq+cq=1;方括号内的3项为负荷组成(第1项为恒阻抗,第2项为恒电流,第3项为恒功率)。
发电机采用的励磁系统如图4所示。图4中:Ut为发电机机端电压测量值,Uref为机端电压给定值,KE为励磁环节放大倍数,TE为励磁环节时间常数,Efd为励磁电压输出值。
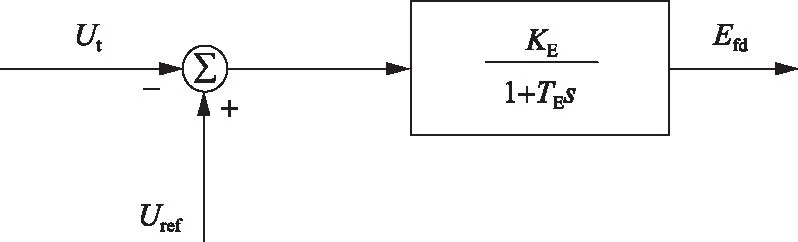
图4 发电机励磁系统传递函数
当图3中的无穷大系统母线与负荷母线间的线路等值电抗XS=0时,系统变为单机无穷大系统;XS=∞时,系统变为单机带负荷系统。可以看出,图3的单机带负荷无穷大系统模型建立了单机无穷大系统和单机带负荷系统之间的联系。
2.2 单机带负荷无穷大系统的线性化模型
以下将图3所示的单机带负荷无穷大系统在运行点处进行线性化处理,并建立其传递函数。
2.2.1 网络部分的线性化
图3中的负荷母线满足以下电流方程(采用发电机dq坐标):
(3)

将式(1)、(2)代入式(3),然后将式(3)在工作点附近作线性化处理,得到方程
ΔId+jΔIq=-j(Id0+jIq0)Δδ+
(4)

根据式(4)可以得到
(ΔUL+jUL0Δα)=
(5)

图3中的发电机满足电压方程
(6)
式中Eq=E′q-(X′d-Xq)Id。
将式(6)在工作点附近作线性化处理,得到方程
(UL0d+jUL0q)Δδ+(X+Xq)(ΔId+jΔIq).
(7)
式中ΔEq为Eq的增量。
将式(5)代入式(7)得到
(8)

由式(8)得到:
ΔId=Kgd1ΔEq+Kgd2Δδ,
(9)
ΔIq=Kgq1ΔEq+Kgq2Δδ.
(10)
式(9)、(10)中Kgd1、Kgd2、Kgq1和Kgq2是根据式(8)得到的系数。
根据Eq=E′q-(X′d-Xq)Id,得到状态量Eq、E′q和Id的增量ΔEq、ΔE′q和ΔId的方程为
ΔEq=ΔE′q-(X′d-Xq)ΔId.
(11)
将式(11)代入式(8)、(9)得到:
ΔId==Kd1ΔE′q+Kd2Δδ,
(12)
ΔIq=Kq1ΔE′q+Kq2Δδ.
(13)
将式(12)代入式(11)得到
ΔEq=Keq1ΔE′q+Keq2Δδ.
(14)

2.2.2 发电机部分的线性化
图3中的发电机三阶实用模型的微分方程为:
(15)
式(15)中:T′d0为直轴暂态开路时间常数;TJ为转子惯性时间常数;Pm为机械功率;Pe为电磁功率;W为阻尼转矩系数;ω0为额定转速;ω为转速。
式(15)工作点附近线性化后的方程为:
(16)
ΔPe=Kpe1ΔE′q+Kpe2Δδ.
(17)
式(16)、(17)中:ΔEfd、ΔPm和ΔPe分别为Efd、Pm和Pe的增量;Kpe1=Iq0Keq1+Eq0Kq1;Kpe2=Iq0Keq2+Eq0Kq2。
根据图4的发电机励磁系统传递函数,得到方程
(18)

根据式(14)、(16)—(18),可以得到单机带负荷接入无穷大系统的传递函数,如图5所示,图中:GGOV(s)为图2所示的调速系统传递函数,GPSS(s)为PSS(如PSS2B型或PSS4B型)的传递函数。

图5 单机带负荷无穷大系统传递函数
图5的传递函数框图和单机无穷大系统的框图基本一致,但系数不同。
3 算例分析
基于单机带负荷无穷大系统及其传递函数模型,可以分析水电机组的超低频振荡模式,以及PSS4B和GPSS抑制超低频振荡的效果和影响因素等。
本文以云南电网某大型水电机组为算例进行分析。建模中机组采用实测参数,励磁系统根据实测参数简化为图4的传递函数,调速系统根据实测参数简化为图2的传递函数,GPSS采用文献[22]的方法得到,PSS4B采用基于频域稳定裕度的参数优化设计方法得到。
3.1 低频振荡和超低频振荡模式的关系
根据图3所示的系统,当无穷大系统母线与负荷母线间的线路等值电抗XS=0时,系统变为单机无穷大系统;XS=∞时,系统变为单机带负荷系统。
在不考虑PSS和GPSS的情况下,采用MATLAB编程,建立图5的传递函数方程,计算得到XS=0~∞时的特征根轨迹,图6给出了与机组的低频振荡和超低频振荡相关的特征根的轨迹曲线。该特征根是1对复数根,为方便显示,图中仅显示其中1个特征根的轨迹曲线。
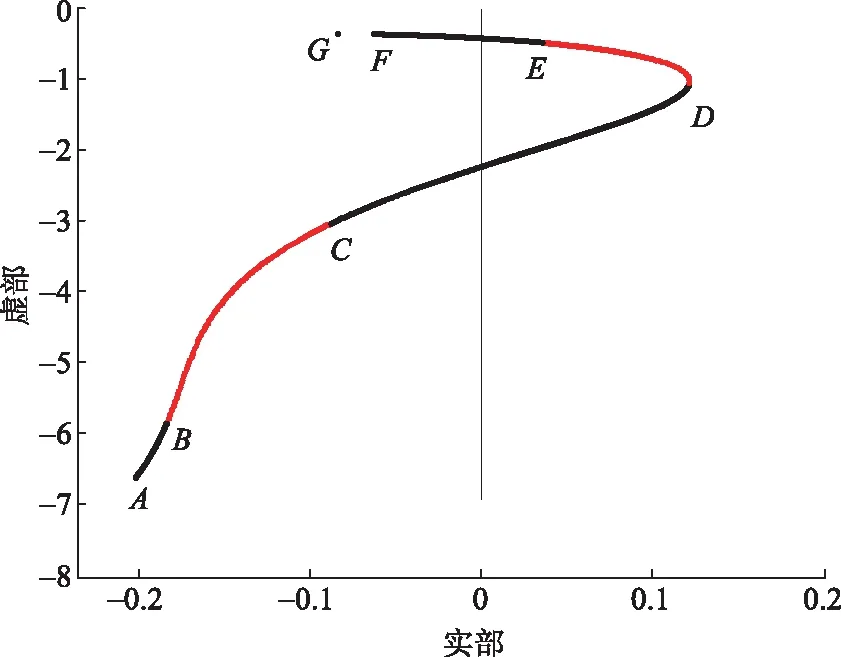
图6 特征根轨迹曲线
图6中点A—F分别对应XS取值为0.01X、X、10X、100X、1 000X和10 000X时的特征根值,其中X为图3发电机与负荷母线间的线路电抗值。点G为XS为无穷大时的特征根值。具体见表1。
XS取值为0.01X,点A对应的是发电机的本机振荡频率。XS取值为无穷大时,点G对应的是发电机的超低频振荡频率。
由表1可以看出,发电机的低频振荡模式和超低频振荡模式是同源的,即2种振荡模式是同一对特征根变化而来。该特征根随着XS/X的增加从低频振荡模式向超低频振荡模式变化。
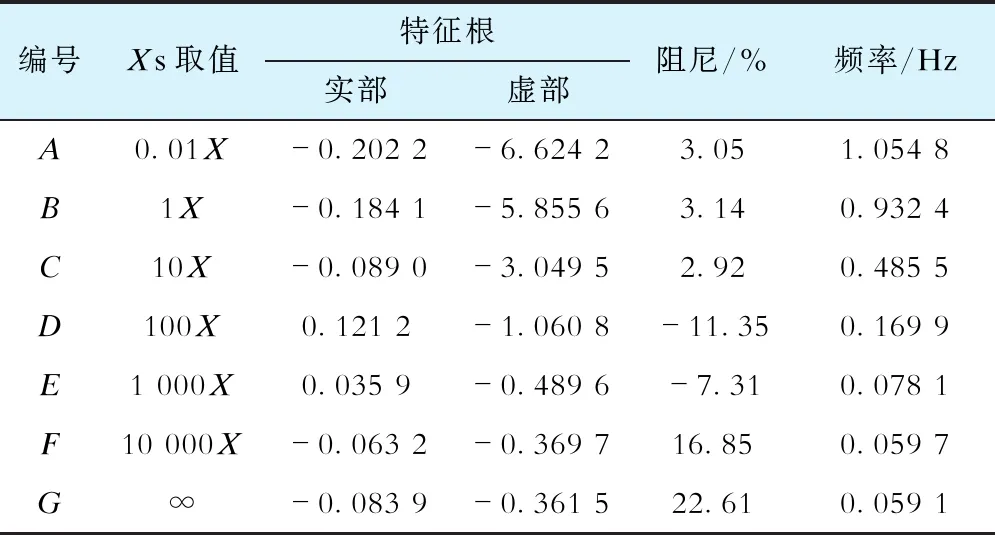
表1 特征根值
以上过程可以理解为:将云南电网等值为由火电机组和水电机组等值机构成的两机系统,其中火电机组侧的等值电抗为XS,水电机组侧的等值电抗为X。当水电机组占比很小时,对应的XS/X很小,此时两机系统近似为单机无穷大系统;随着水电机组占比的增加,XS/X逐渐增加,此时两机系统向单机带负荷系统转化,因此特征根从低频振荡模式向超低频振荡模式的变化可以理解为由系统中水电机组所占比例逐步增加导致。
3.2 PSS抑制低频和超低频振荡的特性
在考虑PSS4B模型的情况下,根据图6的传递函数,将PSS4B的放大倍数逐步增大相同值,观察不同XS取值对特征根轨迹的影响,结果如图7所示。为方便对比,图中保留了图6中的根轨迹曲线。

图7 PSS4B对特征根轨迹的影响
由图7可以看出,随着PSS4B放大倍数的增加,点A—F对应特征值均向左移动至A′—F′,移动距离无明显差异。表明PSS4B对从本机振荡频率到超低频振荡频率之间的频率均有较好的抑制效果。
3.3 GPSS抑制低频和超低频振荡的特性
在考虑GPSS模型的情况下,将GPSS的放大倍数逐步增大相同值,观察不同XS取值对特征根轨迹的影响,结果如图8所示。为方便对比,图中保留图6中的根轨迹曲线。
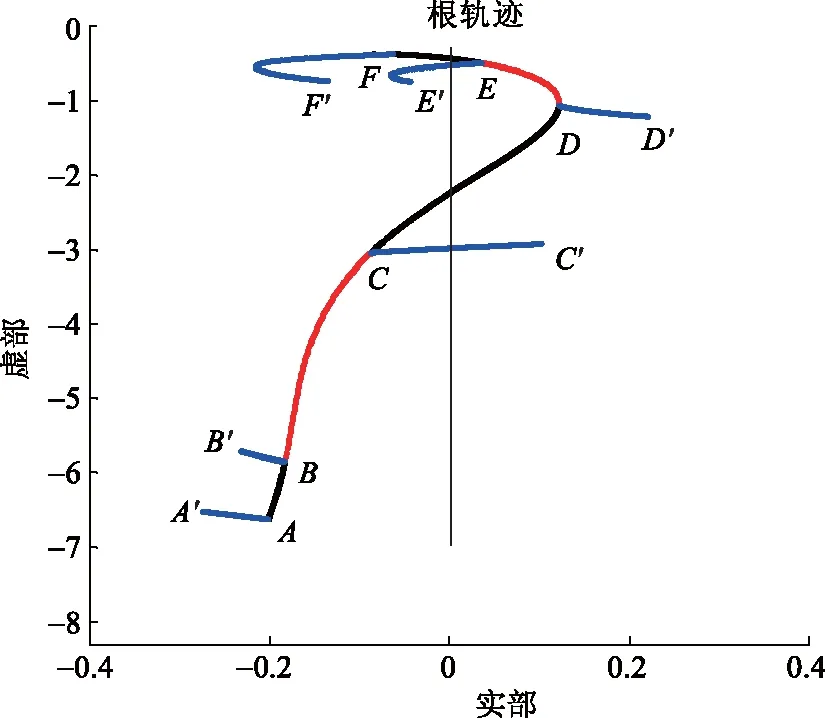
图8 GPSS对特征根轨迹的影响
由图8可以看出:①在超低频段,GPSS可以将特征值向左移动,但随着放大倍数的增大,特征根轨迹存在一个拐点,表明GPSS放大倍数不能过大。②在本机振荡频率附近,GPSS可以将特征值向左移动,表明GPSS不会恶化本机振荡频率附近的阻尼。③对于点C和D对应的0.17~0.5 Hz的振荡频率,这一频段对应云南电网地区间的低频振荡模式,GPSS会将特征值向右移动,即会恶化该频段附近的阻尼。
3.4 PSS4B和GPSS提高阻尼的效果对比
为了对比PSS4B和GPSS这2种基于附加阻尼控制的方式提高机组超低频振荡阻尼的能力,将机组调速器PID控制器的参数设置为云南电网异步运行前的参数,设置XS为无穷大,然后在图5的传递函数中分别投入PSS4B模型和GPSS模型,计算将其放大倍数逐步增大时的根轨迹曲线,结果如图9所示。其中点A是初始运行点超低频振荡频率对应的特征根位置,曲线AC是PSS4B对应的根轨迹曲线,曲线AD是GPSS对应的根轨迹曲线,曲线AB是作为对比给出的机组当前使用的PSS2B对应的根轨迹曲线。
由图9可以看出:①PSS4B具备将超低频振荡模式的阻尼从负值提高到正值的能力。②机组当前配置的PSS2B具备一定的提高超低频振荡模式阻尼的能力,但无法将超低频振荡模式的阻尼提高到正值,说明PSS2B在超低频段的能力有限;PSS4B由于可以专门针对0.1 Hz以下的超低频段进行参数优化配置,因此具备比PSS2B更优的提高超低频段阻尼的能力。③GPSS也具备一定的提高超低频振荡模式阻尼的能力,但随着放大倍数的增加,根轨迹会出现拐点,因此也无法将超低频振荡模式的阻尼提高到正值。

图9 PSS4B和GPSS提高阻尼效果对比
3.5 负荷模型的影响
以上分析中的负荷模型均采用100%恒阻抗模型。进一步分析发现,负荷模型中的负荷组成对PSS4B抑制超低频振荡的效果有影响,而GPSS则不受负荷模型中负荷组成的影响。
图10给出了负荷模型采用100%恒功率模型时,随着PSS4B放大倍数增大时的根轨迹曲线。

图10 100%恒功率下PSS4B对特征根轨迹的影响
通过与图7对比可以看出,随着XS取值的增加,PSS4B抑制低频振荡的效果减弱,在超低频段几乎没有抑制效果。
通过将式(16)、(18)—(20)中的XS取值为无穷大,得到传递函数如图11所示。由图11可以看出,单机带负荷系统的传递函数中与Δδ相关的系数全部变为0。
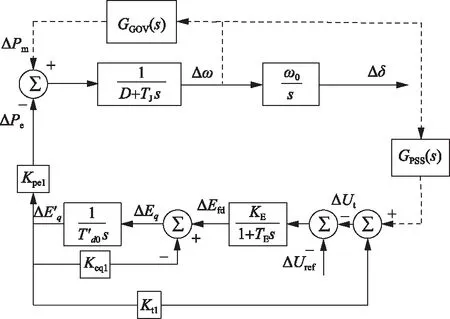
图11 单机带负荷系统传递函数
进一步将负荷模型设为100%恒功率模型,得到的传递函数如图12所示。由图12可以看出,当XS取值为无穷大且负荷模型为100%恒功率模型时,PSS4B对应的反馈环节无法构成闭环,此时PSS4B无法起到作用,而GPSS所在环节则不受影响,从而验证了以上结论。

图12 100%恒功率下单机带负荷系统传递函数
综合以上分析结果可以看出:
a)单机带负荷无穷大系统模型很好地建立了单机无穷大系统和单机带负荷系统之间的联系,可以利用该模型揭示机组低频振荡和超低频振荡的联系,也可以用于定性分析PSS和GPSS抑制超低频振荡的效果。
b)建立的模型适用于分析云南电网这种典型的水电占比较大的电网的低频和超低频振荡问题。
4 结论
本文针对云南电网超低频振荡问题,建立了基于单机带负荷无穷大系统的小干扰分析模型,然后以云南电网某大型水电机组为算例,对PSS4B和GPSS附加阻尼控制用于抑制超低频振荡时的特点和效果进行了对比分析。主要结论如下:
a)发电机的低频振荡模式和超低频振荡模式是同源的,即2种振荡模式是同一对特征根变化而来。该特征根随着XS/X的增加从低频振荡模式向超低频振荡模式变化。这一变化可以理解为系统中电源中的水电机组所占比例逐步增加导致的。
b)PSS4B对从本机振荡频率到超低频振荡频率之间的频率均有较好的抑制效果。在机组调速器PID控制器参数为云南电网异步运行前参数的情况下,PSS4B仍可以将超低频振荡模式的阻尼由负值提高正值,因此采用PSS4B有利于云南电网恢复一次调频特性。
c)PSS4B抑制超低频振荡的效果会受到负荷组成的影响,因此整定PSS4B参数时应考虑云南电网的负荷组成带来的影响。
d)GPSS在超低频段具有抑制效果,也不会恶化本机振荡频率附近的阻尼,但可能会恶化云南电网地区间低频振荡模式的阻尼,并且其抑制效果还存在拐点。在机组调速器PID控制器参数为云南电网异步运行前参数的情况下,GPSS提高超低频振荡阻尼的能力有限。以上是在整定GPSS参数时需要关注的问题。
以上分析结论对云南电网以及其他水电占比较大的电网均具有参考价值,这是基于单机带负荷无穷大系统得到的初步结论,今后会进一步结合云南电网实际情况进行理论分析、仿真和现场验证。
