基于重启动全纯函数嵌入的电力系统经济调度

潘世贤，李志刚，郑杰辉，季天瑶，陈思思

(华南理工大学 电力学院，广东 广州 510641)

如何以经济、安全、可靠的方式调度现有的发电机组以满足用户的负荷需求，一直是电力系统最关注的问题之一。这类优化问题被称为经济调度问题，即在满足负荷需求、机组出力和运行限制等一系列等式和不等式约束条件下，确定电力系统不同发电机组的出力计划，最小化机组的总燃料成本。根据是否考虑爬坡约束等动态约束，可以分为静态经济调度和动态经济调度[1]。用户的负荷需求波动很大，而发电机组的出力受到机组自身及其他条件限制，难以完全实时跟随负荷波动，需要在一段时期内进行优化，因此动态经济调度更符合实际。提高经济调度问题求解算法的准确性、高效性、鲁棒性，可以为电力系统高效运行创造巨大的经济效益。

在求解经济调度问题的算法中：数学规划算法计算速度较快，有严格的理论基础，但是其性能对初始猜测很敏感，容易收敛到局部最优，出现发散时难以确定解的存在性[2]；启发式算法(如遗传算法[3]、差分演化[4]、模拟退火法[5]等)在一定程度上可以跳出局部最优，但计算时间长，算法针对性比较强，具有大量特定参数，鲁棒性差。

近年来，非迭代的全纯函数嵌入式方法(holomorphic embedding method，HEM)凭借良好的性能，受到不少学者的关注，已经被应用到电力系统潮流分析[6]、交直流潮流分析[8]、电压稳定性分析[10]、系统薄弱点识别[11]、连续潮流计算[12]和电气联合网络的动态仿真[13]等方面。HEM本质是一种递归的等式方程组求解器，可以用于求解经济调度问题的Karush-Kuhn-Tucker(KKT)方程，寻找最优的调度方案。在KKT方程嵌入复变量，构造全纯的嵌入式方程；代入展开的变量级数，推导出系数间的线性递归方程，并计算级数的各阶系数；为了加快收敛速度，可以利用帕德近似扩大幂级数的收敛半径，使原问题尽快落在收敛域内，得到满足要求的近似解。当收敛精度高或者系统规模比较大的时候，HEM将消耗较多时间来进行帕德近似计算[6]，而高阶帕德近似计算可能导致近似解停滞，无法进一步收敛到最优[14]。

针对上述问题，本文提出一种用于求解电力系统经济调度的重启动全纯函数嵌入式算法(restarted holomorphic embedding method，RHE)，在HEM中引入重启动机制和启发式规则，使算法仅涉及低阶帕德近似计算，并对不等式约束进行筛选，减小计算规模，同时确定合适的初始值以充分发挥HEM的性能。最后，结合不同规模的静态和动态经济调度问题，对所提出的RHE进行性能测试。

1 经济调度模型

假设求解的电力系统包含NB个节点、NG个发电机组和NF条输电线路。

1.1 目标函数

经济调度以最小化调度期间的发电机组总燃料成本F为目标[15]，即

(1)

式中：t为调度时段；T为调度时段个数；Q、C、k分别为发电成本的二次项、一次项和常数项系数；Pt为发电机组在时段t的有功出力(下标t表示时段t，下同)。

1.2 约束条件

经济调度问题的约束条件可以表示为[16]：

(2)

式中：Bbus、BF分别为节点导纳矩阵、支路导纳矩阵；列向量Θt、Dt分别为节点电压相角和有功负荷；CG为发电机关联矩阵，当发电机g连接在节点h，其元素(g,h)为1，否则为0；Fmax为线路允许传输功率上限；Pmin、Pmax分别为发电机组出力的下限、上限；Rt为发电机组的最大爬坡功率。式(2a)为基于直流潮流的功率平衡方程，式(2b)为线路的传输约束，式(2c)、(2d)分别为发电机组的出力约束和爬坡速率约束。

相比于仅考虑系统输出总有功功率与总负荷平衡关系的经济调度模型[18]，本文采用基于直流潮流的功率平衡方程，考虑了电网架构对潮流分布的影响，模型更准确。

1.3 模型求解

通过引入非负的松弛变量Z将不等式约束转换为等式约束，得到经济调度问题形式为：

(3)

式中：λt、μt分别为对应约束条件的等式、不等式拉格朗日乘子；下标F、G、R分别表示线路传输约束、发电机容量约束以及爬坡约束，上标+、-分别表示约束的上限、下限，下同。

对于时段t，令Ht为等式约束、Gt为不等式约束，则经济调度问题的拉格朗日函数

(4)

问题对应的KKT方程为：

(5)

2 HEM

对于KKT方程，可以利用HEM求解，主要包含4个步骤。

2.1 步骤1：构造嵌入式方程

在式(5)中嵌入复变量s，构造全纯的嵌入式方程为

L(X(s))=L(X(0))+s(RHS-L(X(0))).

(6)

式中X(s)为关于s的函数。s=0时，式(6)恒成立，X(0)为可以任意选取的变量初值。

X(s)可以展开成麦克劳林级数[19]：

(7)

式中X[k]为级数的第k阶系数。可以推导出，变量级数的常数项等于变量初值，即X[0]=X(0)。

2.2 步骤2：求解幂级数系数

将式(7)代入到式(6)中，可以推导出线性的递归方程为

AX[n]=B[n-1].

(8)

式中：X[n]为变量幂级数的第n阶系数；其余项仅涉及前n-1阶系数，移到等式右侧构成右端项B[n-1]；A为系数矩阵，仅包含常数项，不会随着n改变，其表达式如式(9)所示，其中μt、Zt取初值，D(a)表示将向量a对角化，EG为单位矩阵。当n=1时，B[0]=RHS-L(X(0))；当n≥2时，右端项B[n-1]如式(10)所示。

(9)

(10)

2.3 步骤3：计算帕德近似

为了将幂级数的收敛域扩展到最大，解析延拓一般选取对角或近似对角的帕德近似，即

(11)

2.4 步骤4：判断收敛条件

采用常规的方程组最大不匹配度Mi来判断收敛，对于不等式约束只需判断是否满足条件，收敛判据为

max(Gt),‖μtZt‖∞)≤ε.

(12)

(13)

如果近似解满足收敛条件，将其作为原问题的解输出；如果不满足收敛条件，则返回步骤2计算更高阶的系数，重新计算新的帕德近似值。

3 RHE

HEM的运行时间主要消耗在帕德近似计算，当收敛精度高或者计算大规模系统时，帕德近似需要计算到非常高阶，不仅耗时长，还可能在不满足收敛精度的近似解停滞不动[14]。动态经济调度问题需要优化整个调度时段的机组出力，涉及的计算量很大，直接利用HEM进行求解时，求解速度可能很慢。考虑到在求解过程中，有部分不等式约束在多数情况下不起作用，可以先不考虑它们，放开相应的限制，求解一个可行范围更大但计算规模较小的新问题。通过降低问题的求解规模，提高算法效率。

本文在HEM中引入重启动机制和启发式规则，提出了用于求解动态经济调度问题的启发式全纯函数嵌入算法。RHE设定幂级数系数的最高次数nmax，将计算过程分为初始过程和重启动过程。初始过程中，当系数计算到最高次数算法仍未收敛时，停止计算更高阶系数，进入重启动过程。重启动过程中启发式规则利用上一过程得到的近似解，筛除优化问题的不等式约束，简化当前过程中需要求解的问题，并为构建的新问题选取合适的初始值。

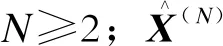
3.1 初始过程

(14)

将近似解代入式(12)判断是否收敛，不满足时算法进入重启动过程。

3.2 重启动过程

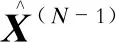
当I为空集时，重启动过程暂时无需考虑额外的不等式约束，变量初始值选取为上一过程的近似值。

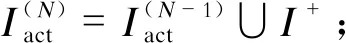
将考虑的不等式约束和对应的互补条件添加到方程组式(14)中，构成当前过程求解的方程：

(15)

确定好方程和初值后，式(15)可依据第2章的HEM进行求解。构造与式(6)同形式的嵌入式方程，则推导出递归方程AactX[n]=Bact，其中系数矩阵

(16)

(17)

右端项Bact由式(10)的对应行组成，

(18)

在重启动过程中，障碍因子不断更新，逐步逼近0，即

(19)

为了防止问题无解时算法一直发生重启，需设定最大重启动次数Nmax。当重启动次数达到最大依旧未计算到收敛解，输出结果不收敛。RHE无需事先确定初始值，初始过程的线性方程组可以直接求解，重启动过程的初值由启发式规则确定。

重启动机制使该算法只涉及到低阶帕德近似计算，避免了高阶帕德近似计算的高耗时和停滞解问题；启发式规则能够根据上一过程的近似解，筛选可能起作用的约束加入方程组进行求解，同时确定合适的初始点，降低了解方程的规模，提高了HEM的计算效率。

RHE的计算流程如图1所示。

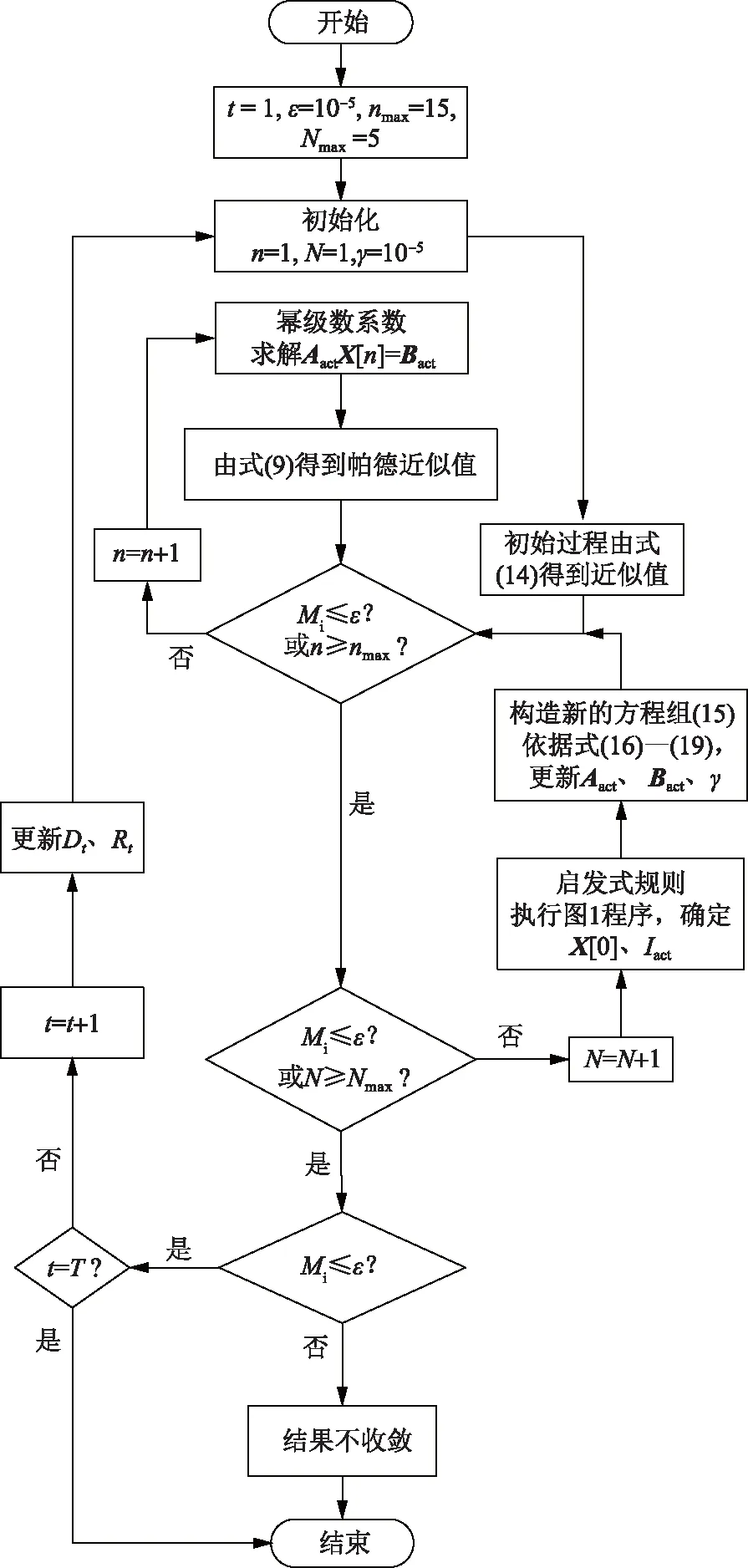
图1 RHE的计算流程

4 算例测试

为了验证RHE的性能，结合不同规模的静态和动态经济调度问题进行测试。所有测试都在MATLAB平台上建模实现，并在硬件配置为Intel 3.0 GHz四核处理器和8 GB RAM的计算机上进行仿真。为了验证本文提出方法的准确性，以MATPOWER包的内点法(MATPOWER interior point solver，MIPS)作为基准[21]，同时结合基于传统经济调度的HEM(HE method bases on the primitive economic dispatch，EDHE)进行分析[22]。设收敛精度ε=10-5，幂级数系数最高次数nmax=15，重启动最高次数Nmax=5。

4.1 静态经济调度

为了研究RHE的有效性和重启动机制对算法的影响，利用RHE求解不考虑爬坡约束的静态经济调度问题。为了便于与EHDE对比，使用与文献[22]相同的算例进行测试，系统的信息汇总见表1。每新增3个幂级数系数进行1次帕德近似，视为1步递归计算。

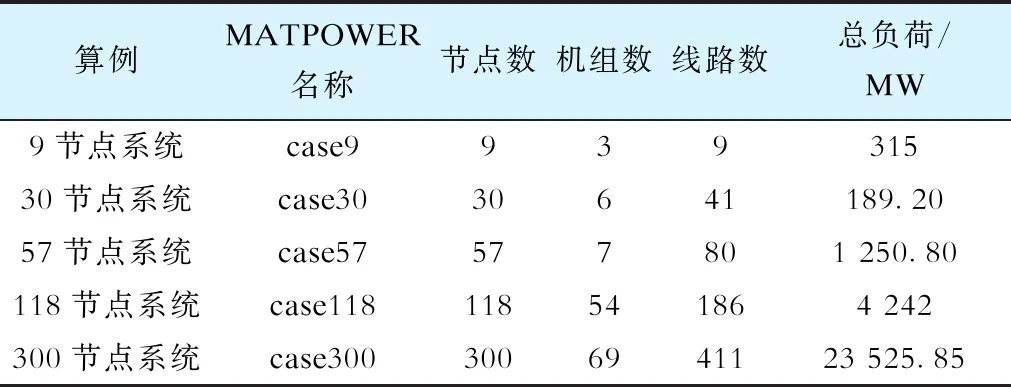
表1 静态经济调度的测试算例

图2、图3分别是RHE和EDHE的不匹配度变化情况。2种方法都能在10步内达到收敛精度，RHE的步数明显少于EDHE，说明重启动机制能有效提高收敛速度。

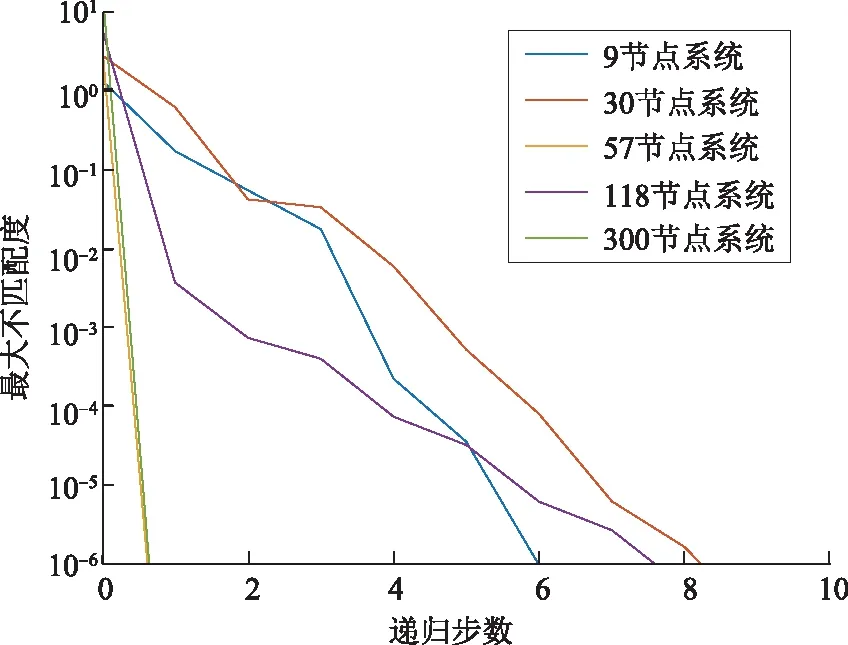
图3 EDHE的不匹配度

比较RHE和MIPS、EDHE在发电成本和有功出力上的差异，结果见表2、表3。发电成本的最大误差在4.1×10-5美元以内，有功出力误差不超过5.6×10-8MW，这个计算误差可以忽略不计，说明3种方法都能准确收敛到同一最优解。

表2 RHE与MIPS的计算误差

表3 RHE与EDHE的计算误差

表4统计了RHE、EDHE、MIPS求解不同算例的执行时间。RHE的耗时基本少于EDHE和MIPS。求解57节点系统时，RHE耗时略高于EDHE，但相较于MIPS，两者的执行时间都较短。相比于其他4个算例，RHE计算IEEE 118节点系统的时间明显更长，这是因为在求解过程中多执行了一个重启动过程，但耗时依旧少于EDHE。

通过与MIPS、EDHE对比，验证了RHE的计算准确性和良好的收敛特性。引入重启动机制，明显提高了收敛速度，减少了算法的执行时间。

4.2 动态经济调度

为了进一步验证RHE的性能，结合改进IEEE 14节点和300节点系统的动态经济调度问题进行测试，考虑调度时长为24个时段(1 h为1个时段)的调度问题。发电机成本参数和负荷需求见附录A。

附录A

4.2.1 IEEE 14节点系统

在IEEE 14节点系统中，为了测试RHE求解动态经济调度问题的性能，设计3种爬坡约束限制，分别为发电机组当前容量的25%(算例1)、18%(算例2)、10%(算例3)。

利用RHE和MIPS分别求解以上3个算例，仿真结果表明2种方法的最大不匹配度都能达到收敛精度要求。表5给出RHE与MIPS的计算误差，发电成本的误差在3.1×10-6美元以内，有功出力的误差不超过2.0×10-6MW，说明2种方法成功收敛到同一个最优解。

表5 RHE与MIPS的计算误差(算例1、2、3)

各个发电机组在每个调度时段的有功出力如图4所示。算例1中，发电机组的爬坡速率限制足够宽松，没有动态约束起作用，能够根据负荷需求以最经济的方式进行功率分配。算例2中，机组4的爬坡约束在5个时段起作用，机组5的爬坡约束只在1个时段起作用。算例3中，5个机组的爬坡约束均有起作用。表6列出了机组爬坡约束起作用的具体时段。

表6 发电机组起作用的爬坡约束

随着发电机组爬坡约束限制不断收紧，相邻时段内功率可变化的范围缩窄。为了保持系统功率平衡，功率分配占比高的机组的出力曲线波动较大，峰谷更加明显，如机组2；功率分配占比低的机组的出力曲线相对平缓，如机组4。动态约束起作用后，系统功率分配的经济性下降，发电成本有所上升，从算例1到算例3的成本逐渐升高。

接下来分析2种方法的收敛速度。图5给出了RHE、MIPS算法的最大不匹配度随递归步数、迭代步数的变化情况。随着动态约束起作用，2种方法所需的计算步数都会增多，其中RHE的变化更明显：MIPS需要8～10步才能收敛；RHE的步数从不到4步增加到7步。总体表现上，RHE具有更好的收敛速度。

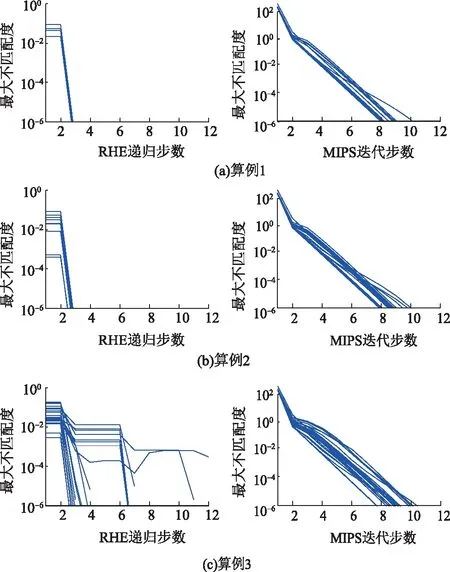
图5 IEEE 14节点系统最大不匹配度

RHE和MIPS计算3个算例的执行时间见表7。考虑到帕德近似计算的高度可并行性，可以从总执行时间中剔除其计算时间，得到调整时间，这个时长更具有代表性[6]。无论忽略与否，RHE的耗时都明显少于MIPS；此外，RHE求解算例3的耗时明显增加，是因为起作用的动态约束增多，需要更多重启动过程才能收敛。

表7 IEEE 14节点系统的执行时间

4.2.2 IEEE 300节点系统

在IEEE 300节点系统中，同样设计3个不同爬坡约束限制的算例，测试RHE求解大规模系统的性能。速率限制分别设定为发电机组当前容量的25%(算例4)、20%(算例5)、10%(算例6)。

RHE和MIPS的计算误差见表8。虽然算例6的发电成本误差数量级在10-4美元，但相对于数量级在107美元的总成本，这样的误差可以忽略不计。2种方法的有功出力误差也非常小，它们成功收敛到同一个最优解。

表8 RHE与MIPS的计算误差(算例4、5、6)

表9列出了机组爬坡约束起作用的时段。25%爬坡速率限制下，测试系统中有13个机组的爬坡约束起作用，在无限制下速率可能超过25%，影响到发电机的运行寿命，实际运行中有必要对爬坡速率进行限制。随着爬坡约束的收紧，约束起作用的机组明显增多，算例6中只有13个机组没有受限；同一机组约束起作用的时间也逐步延长。

表9 发电机组起作用的爬坡约束

2种方法的最大不匹配度如图6所示。MIPS达到收敛的计算步数主要分布在8～10步或16～20步；RHE的步数分布较分散，主要在4步或者16步左右，需要的步数一般少于MIPS，表现出更好的收敛速度。

图6 IEEE 300节点系统最大不匹配度

2种方法的执行时间见表10。RHE的总执行时间多于MIPS，但是其忽略帕德近似计算后的调整时间略少于MIPS，两者相差不大，这也说明帕德近似计算占据了HEM的大部执行时间(尤其系统规模较大时)。RHE采用的是常规的帕德近似方法，已有文献提出更高效的帕德近似方法[23]，计算时长可以压缩到原来的1/6以下。考虑并行运算时，仍然可以采用调整时间作为近似耗时。

表10 IEEE 300节点系统的执行时间

5 结束语

本文提出了一种求解电力系统经济调度问题的RHE。在常规全纯嵌入算法中引入了重启动机制和启发式规则，该算法只涉及到低阶帕德近似计算，减少了计算高阶帕德近似的时间，同时避开了近似解可能停滞的情况；在每个重启动过程中，筛选可能起作用的约束加入方程组进行求解，无需计算完整的KKT方程，降低了方程的求解规模，同时可以为HEM求解方程提供合适的初始点。

经过测试，验证了该算法能高效、准确地求解静态和动态经济调度问题。求解静态经济调度问题时，RHE的表现优于EDHE和MIPS。在求解动态经济调度问题方面，与MIPS相比：计算小规模系统时，RHE在收敛速度和执行时间上具有明显的优势；计算大规模系统时，RHE需要消耗很多时间去计算帕德近似，不考虑这部分可并行运算的时间，RHE在收敛速度和执行时间上仍有优势。

未来的工作可以着眼于：①使用更准确的交流潮流模型，考虑合约出力约束等更多动态约束；②提高算法的计算性能，开发更高效的帕德近似计算方法，实现并行运算。