基于改进RRT的智能巡检机器人狭窄通道路径规划*

陈法法，蒋 浩，李 振，肖文荣，陈保家

(三峡大学水电机械设备设计与维护湖北省重点实验室，宜昌 443002)

0 引言

巡检机器人通过在传统机器人上安装各类传感器，实现对在役设备的日常巡查。通过机器人的智能巡检，可以及时发现在役设备在运行过程环节中的异常事件和安全隐患，帮助运维人员准确掌握设备故障的初期信息[1]。智能巡检机器人已经广泛应用于石化、燃气、电厂、铁路等行业， 大大减轻了巡检员高频、高强度和低脑力的日常巡检任务[2]。尽管智能巡检机器人在各个行业均取得了一定成功，然而在面对一些特殊的巡检任务，如：当应用场景中存在密集的障碍物、通道狭窄时依然存在一定的局限性[3]，其平顺性、稳定性、快速性等性能均出现不同程度的下降[4]。智能巡检机器人平稳通过狭窄通道在很大程度上取决于其路径规划算法[5]，通过高效的路径规划算法可以得出一条穿过狭窄通道的最优路径而不碰撞障碍物[6]。近年来，快速搜索随机树(rapidly-exploring random tree，RRT)的发展为巡检机器人在狭窄通道处的路径规划提供了一种新的思路，它具备在未知空间中找到一条合适路径的能力。同时，针对于RRT算法存在的一些不足，许多研究学者改进出了不同的方法。

KARAMAN等[7]针对RRT算法搜索速度慢的问题，改进出了RRT*算法，该算法在继承 RRT概率完备性的同时具备渐进最优性；QURESHI等[8]在RRT算法基础上改进了基于多树搜索的双向搜索算法(Bi-RRT)，提高节点的扩展效率和算法的收敛速度；然而上述改进算法只提升了搜索速度，无法避免陷入局部最优的问题；阮晓钢等[9]结合三种子目标搜索策略，改进出了一种基于子目标搜索的机器人目标导向 RRT路径规划算法，使机器人具有逃离局部极小环境的能力；JEONG等[10]通过扩大 RRT*算法重选父节点和剪枝的范围，改进出了一种Quick-RRT*算法；但是上述算法只能针对一般复杂的地图环境，却无法有效通过狭窄通道；付久鹏等[11]结合RRT-connect算法与桥测试算法，通过在两个障碍物中间“架桥”的方式自动探寻狭窄通道的入口；钟建冬等[12]利用星形试验法辨识出狭窄通道形状，增加了狭窄通道中的路标密度，提高了通过狭窄通道的概率；孙逸武[13]设计了一种A*-RRT算法，能够快速定位到初始节点和目标节点，通过A*算法在狭窄通道中循迹并形成最终路线。

上述算法能在一定程度上提高巡检机器人通过狭窄通道的概率，但是各类改进算法也存在占用内存空间大、搜索效率低、采样节点利用率不充分等局限性。为此，本文在深入分析上述算法的基础上，设计了一种面向狭窄通道的多次根节点快速扩展随机树算法(multiple second root-RRT*，MS-RRT*)，旨在找出场景中的狭窄空间区域，从而对该区域进行合理化扩展。其核心思想是采用多个有限扩展次数的根节点生成局部扩展树，使用局部扩展树实现对局部区域的扩展，同时通过不断重启和生成多个次根节点，找到狭窄通道区域，进而减少采样节点落在障碍物中的数量，提高通过狭窄通道的概率。实验结果表明，本文算法中，采样节点落在障碍物中的数量明显减少，巡检机器人通过狭窄通道的性能明显提高。

1 RRT*算法原理

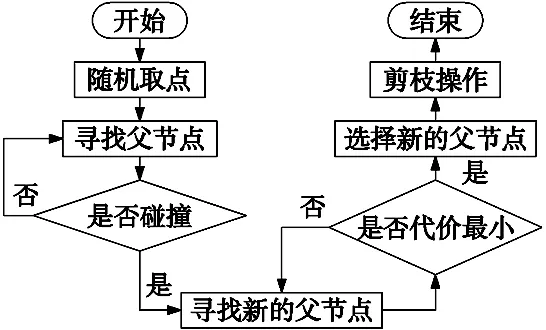
图1 RRT*算法流程示意图

RRT算法[14]以初始节点为根节点进行增量式地扩展随机树，同时避开障碍物[15]。RRT*算法在RRT算法的基础上，增加重新选择父节点与剪枝优化过程[16]以保证路径的最优性。RRT*算法的流程图如图1所示。 RRT*算法的伪代码如表1所示。

表1 RRT*算法伪代码

从图1和表1可以看出， RRT*算法使用CollisionCheck函数得到符合条件的qrand之后，将符合条件的qrand加入到搜索树T中[13]，记此时qrand为qnew，其父节点变为qnearest。

当得到qnew之后，通过Near函数，RRT*会启动重选父节点过程[14]，以qnew为中心，R为半径找到在搜索树T中的一系列节点Vnear，并计算出qnew经过Vnear中的任一节点到达根节点qinit的代价值。随后使用Chooseparent函数选定Vnear中代价值最小的节点作为qnew新的父节点[15]，并插入到搜索树T中。RRT*算法通过Rewire函数对搜索树T实现剪枝优化策略。

传统RRT*从根节点开始，采用随机采样的方式扩展搜索树T。在复杂环境地图下，随机采样节点易落在障碍物中，节点使用率低，影响搜索树T生成效率[17]。同时，在狭小空间处，不能稳定的得到一条合适路径。

2 MS-RRT*算法

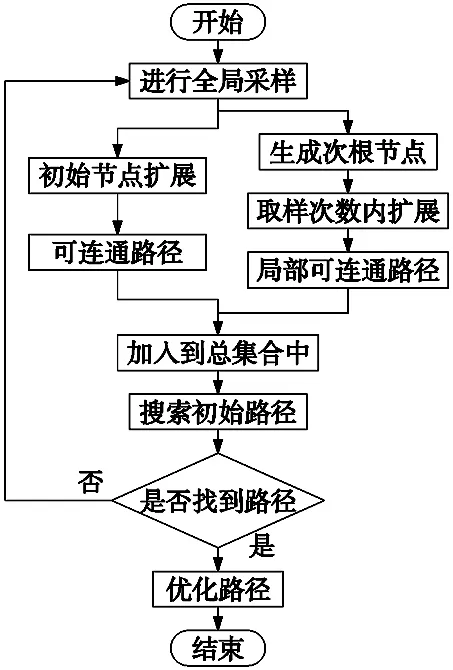
图2 MS-RRT*算法流程示意图

针对RRT*算法在复杂环境地图下节点使用率低、不能有效生成路径的问题[18-19]，设计了一种面对狭小空间的多次 根节点快速扩展随机树算法(multiple second root-RRT*，MS-RRT*)，以期提高RRT*算法采样节点的使用率，增强算法的完备性。基本原理如下：首先通过生成局部的次根节点，形成局部可连通路径，减少采样节点落在障碍物上的概率，提高采样节点用率；然后找出在狭窄通道附近的次根节点，将次根节点不断的优化，实现对狭窄通道探索，提高通过狭窄通道的成功率；最后，通过在全局地图中不断的迭代搜索，并采取优化路径策略，得到一条从起点到目标点的代价小、无碰撞的最优路径，该算法的流程如图2所示。

2.1 基于次根节点的局部搜索策略

本算法在RRT*算法基础上，通过设置多个次根节点来进一步提升算法性能。设Qfree为无障碍区域，Qobs为障碍区域，在无障碍区域Qfree中随机生成M个次根节点ai，N={a1,a2…ai…aM}。设置总的探索次数为有限值K。当前的探索次数为变量t，此时次根节点ai可记为ai,t。

以次根节点ai,t为中心在周边区域进行探索，当找到最小的可连通路径Tdi为止，所有次根节点生成的最小可连通路径的集合记为T。设置次根节点ai,t的权重为wB(i)，wB(i)越大，表明该区域生成最小可连通路径Tdi越困难。将wB(i)标准化，使得在点集N中的所有ai,t对应的wB(i)之和为1。

同时，次根节点ai,t在生成最小可连通路径Tdi时，也设置奖励值R(ai,t)。当采样成功时R(ai,t)的取值为0，失败时为1。通过次根节点总的奖励值R(ai,t)得到其wB(i)，步骤如下：

步骤1：计算次根节点ai,t连接失败的概率：

(1)

步骤2：点集N中所有节点权重wB(i)与p(ai,t)一致，为使得wB(i)总和为1，对wB(i)做标准化处理：

(2)

次根节点ai,t的权值wB(i)判断该次根节点落在可连通路径上的概率，当权值wB(i)越大，表明该次根节点落在狭窄通道区域的概率越大。当次根节点ai,t当前采样次数t为K时，MS-RRT*算法根据次根节点的权值wB(i)判断是否给该次根节点赋予新的采样次数。

表2 次根节点探索算法伪代码

探索算法中，首先判断次根节点ai,t是否符合条件，随后开始迭代。以次根节点ai,t为中心，在ai,t附近生成一个采样点qrand，对qrand和ai,t使用CollisionCheck函数实行碰撞检测，在可以生成可连通路径的前提下将qrand加入到搜索树Tdi中。随后以qrand作为新的次根节点，以此类推。

图3 窄小通道采样示意图

狭窄通道的采样示意如图3所示，图3中，次根节点为ai,t，虚线圆是次根节点的采样区域，采样点1～3是次根节点ai,t在狭窄通道中的扩展节点。根据算法3，在逐次迭代过程中，节点3变成新的次根节点ai,t，在节点3处继续扩展，得到采样节点4，落在了障碍物Qobs中，连接失败。随后生成采样节点5，同样连接失败，次根节点ai,t继续扩展得到采样结点6，此时采样节点6落在自由空间Qfree内。此得到一条通过狭窄通道的局部搜索树Tdi，Tdi包含初始节点在内的节点1、2、3和6。

2.2 基于次根节点再选择的全局搜索策略

MS-RRT*算法通过不断重启和生成局部的次根节点，对全局地图中复杂环境狭窄通道的探索。

表3 次根节点再选择restart算法

MS-RRT*算法通过对点集N中数量为M的次根节点ai,t所对应权重值wB(i)进行正向排序，选取前P个次根节点加入到新的点集中并重新赋予新的采样次数；随后将每次次根节点ai,t得到的局部搜索树Td加入搜索树集合T中；当初始节点qinit和目标节点qgoal通过搜索树T实现连接后，则生成一条从初始节点qinit到达目标节点qgoal的可行路径。同时，停止对次根节点的再选择策略。

2.3 优化策略

生成一条可行路径后，MS-RRT*算法将停止重启和生成新的次根节点ai,t。随后，以初始点qinit为起点采取重选父节点的操作，按照规定步长选取qinit附近空间的采样点qrand，在可以生成可连通路径的前提下，将采样点加入到可行路径集合中。

若采样点qrand加入到可行路径中后，可行路径的长度小于集合中现有的路径长度，则该采样点qrand作为新的父节点加入路径中，按照次序对路径中下一采样点进行该操作，最终得到最优路径。

3 实验与分析

为了验证本文所设计算法的有效性和优良性能，通过本文算法与RRT*算法和Bi-RRT*算法以及Informed-RRT*算法[20]进行对比实验，实验中的电脑配置：处理器为Inter(R)Core(TM) i5-11400 CPU @2.70 GHz，16.00 GB内存，Windows11操作系统。

基于python3环境，各个对比算法的参数设置如下：最大迭代次数为5000次，实验次数10次，每次生成的次根节点个数为16个，最大扩展次数为10次，每次扩展时扩展次数增加1次。

3.1 狭窄通道路径规划的有效性对比

图4 包含多层狭窄通道的地图map1

(1)地图构建。为了验证狭窄通道路径规划的有效性，构建包含多层狭窄通道的简单地图如图4所示，该地图中黑色区域为障碍物空间Qobs，白色区域为无障碍物空间Qfree。实验过程中，希望得到一条从初始节点经过白色自由空间到达目标节点的无障碍路径。

(2)结果对比。实验结果如图5～图8所示，图中黑色点为初始节点qinit，灰色点为目标节点qgoal，黑曲线为算法最终得到的路径。

原始RRT*算法在狭窄空间地图map1下的实验结果如图5所示，从图5可以看出，从初始节点到目标节点的取样过程中，取样节点的分布逐渐稀疏。在初始节点附近，生成了大量的取样点，降低了探索效率。当单向扩展树进入到狭窄通道后，由于包含多层狭窄通道，在有限的迭代次数内甚至无法得到连通路径。

原始Bi-RRT*算法在狭窄空间地图map1下的实验结果如图6所示，从图6可以看出，在地图的中间区域，取样节点的分布比在初始节点和目标节点附近稀疏。由于初始节点和目标节点双向扩展的过程中，在各自节点附近生成了大量的取样点，使得取样效率降低。当双向扩展树进入到狭窄通道后，在有限的迭代次数也极有可能无法得到有效的连通路径。

图5 RRT*算法在地图map1中实验结果 图6 Bi-RRT*算法在地图map1中实验结果

Informed-RRT*算法在狭窄空间地图map1下的实验结果如图7所示，从图7可以看出，算法在初始节点附近生成了大量的取样点，使得取样效率降低，图中红色为使用椭圆优化策略的图样，可以看出，优化策略的结果并不明显。

本文所设计的MS-RRT*算法在狭窄空间地图map1下的实验结果如图8所示，图8中灰色大点为初始节点qinit，灰色小点为随机采样节点，黑色和浅灰色点为随机生成的次根节点。算法开始运行后，除初始节点随机生成采样节点外，所有的次根节点也随机生成采样节点，并且随着探索次数的增加，次根节点的颜色由浅灰色逐渐变成黑色。

图7 Informed-RRT*算法在地图map1中实验结果 图8 本文算法在地图map1中实验结果

从初始节点到目标节点的单向扩展过程中，借助次根节点探索大大提升了得到可连接通道的概率，减少了取样节点落在障碍物上的概率。由于采用了重启和再选择次根节点的策略，也有效排除了性能低劣的次根节点，进一步提升了取样效率。

为了进一步定量分析，本文采用了探索成功率、路径成本均值、首次探索到合适路径平均时间、取样节点在障碍物中数量、总耗费平均时间等指标进一步分析。

(1)探索成功率。探索成功率是衡量算法有效性的一个指标，其值越大，算法在狭窄通道路径规划的有效性越高。在第j次实验中是否得到连通路径记为H(j)，H(j)的取值为0时，代表未能得到连通路径，H(j)的取值为1时，代表得到连通路径；实验总次数为D；探索成功率为P。

(3)

(4)

(5)

(3)首次探索到合适路径平均时间。首次探索到合适路径的耗费时间是衡量算法效率的一个重要指标，其值越小，算法在狭窄通道找到合适路径的效率越高。由于算法有机率无法探索到合适路径，因此，本算法中首次探索到合适路径平均时间代表在得到连通路径的情况下，首次探索到合适路径时间的均值。

(4)取样节点在障碍物中数量。取样节点在障碍物中数量反应算法的取样效率，数量越多，表明算法在生成可连通路径的过程中，浪费的取样节点数量越多。由于算法采用随机生成取样节点的方式，取样节点可能落在障碍物区域Qobs中，也可能落在无障碍物区域Qfree中，落在障碍物区域的取样节点无法使用，造成了取样节点的浪费。

(5)总耗费平均时间。总耗费时间表明算法在有限迭代次数下，算法运行过程中耗费的时间，反应算法在进行路径规划时的效率，其值越小，表明算法的效率越高。在本文中，无论算法是否在狭窄通道中探索到有效路径，在有限迭代次数下，算法仍有一个运行时间。因此，总耗费平均时间代表算法在有限迭代次数在，运行时耗费时间的平均值。

4种算法在地图map1的对比实验如表4所示，从表4中可以看出，4种算法的路径成本均值相差不大，但是在探索成功率、取样节点在障碍物中数量等指标方面，本文算法的优势十分明显。本文设计的MS-RRT*算法，较之原始RRT*算法，其取样节点落在障碍物中的数量减少了29.36%；较之原始Bi-RRT*算法，其取样节点落在障碍物中的数量减少了42.83%；较之Informed-RRT*算法，其取样节点落在障碍物中的数量减少了38.43%。在路径探索的成功率上，本文提出的算法达到了100%，远高于RRT*算法的63.33%和Bi-RRT*算法的90%以及informed-RRT*算法的60%。在首次探索到合适路径平均时间上，本文提出的算法所耗费的时间相较于原始RRT*算法减少了90.45%，相较于Bi-RRT*算法减少了60.37%，相较于Informed-RRT*算法减少了89.56%。在总耗费时间上，本文提出的算法所耗费的时间相较于原始RRT*算法减少了35.55%，相较于Bi-RRT*算法减少了35.4%，相较于Informed-RRT*算法减少了36.67%。

表4 4种算法在地图map1的实验仿真结果

3.2 狭窄通道路径规划的优良性对比

图9 含有多个障碍物的狭窄空间地图map2

(1)地图构建。为了验证多次根节点算法对于狭窄通道路径规划的优良性，构建多障碍物组成的狭窄通道简单地图如图9所示，该地图中黑色区域为障碍物空间Qobs，白色区域为无障碍物空间Qfree，该地图中含有多个障碍物，且初始节点到目标节点包含多条可行路径。实验过程中，希望得到一条从初始节点经过白色自由空间到达目标节点的无障碍路径。

(2)结果对比。实验结果如图10～图13所示，图中红色点为初始节点qinit，绿色点为目标节点qgoal，蓝色线段为算法最终得到的路径。

原始RRT*算法在狭窄空间地图map2下的实验结果如图10所示，从图10可以看出，在多障碍物地图环境下，从初始节点到目标节点的取样过程中，取样节点的分布仍然是逐渐稀疏。但是由于地图map2中存在多种可行通道，原始RRT*算法在有限的迭代次数下，仍能够得到有效的连通路径。

原始Bi-RRT*算法在狭窄空间地图map2下的实验结果如图11所示，Bi-RRT*算法将初始节点区域和目标节点区域得到了充分探索，但是在地图的中间区域，仍未能充分探索。

图10 RRT*算法在地图map2中实验结果 图11 Bi-RRT*算法在地图map2中实验结果

Informed-RRT*算法在狭窄空间地图map2下的实验结果如图12所示，图中可以看出，算法的优化策略在地图中开始扩展，但是在地图map2中的效果并不明显。

本文所设计的MS-RRT*算法在地图map2下的实验结果如图13所示，比较图10～图13可以看出，本文算法从初始节点到目标节点的单向扩展过程中，借助次根节点对地图map2的各个狭窄通道处实现探索，因而在得到合适路径后，通过后续的路径优化策略，得到路径距离更优。

图12 Informed-RRT*算法在地图map2中实验结果 图13 本文算法在地图map2中实验结果

表5是采用了探索成功率、路径成本均值、首次探索到合适路径平均时间、取样节点在障碍物中数量、总耗费平均时间等指标进一步分析的实验结果，4种算法的路径成本均值和探索成功率相差不大，在首次探索到合适路径平均时间指标上，本文算法和Bi-RRT*算法差不多，但是比RRT*算法减少了73.6%，比Informed-RRT*算法减少了38%。并且，在总耗费平均时间和取样节点在障碍物中数量指标方面，本文算法的优势十分明显。设计的MS-RRT*算法，较之原始RRT*算法，其总耗费平均时间减少了35.24%；较之原始Bi-RRT*算法，其总耗费平均时间减少了37.4%，较之Informed-RRT*算法，其总耗费平均时间减少13.65%。取样节点在障碍物中数量指标上，本文算法相较于RRT*算法减少了16.77%，相较于Bi-RRT*算法上减少了19.83%，相较于Informed-RRT*算法上减少了34.95%。

表5 4种算法在地图map2的实验仿真结果

综合两种地图的对比实验可以看出，本文算法探索可连通路径时，在整个连通路径上，取样节点的分布更加均衡，出现过度取样和欠缺取样的概率大大降低。在定量指标上，探索成功率、路径成本均值、首次探索到合适路径平均时间、取样节点在障碍物中数量、总耗费平均时间等指标也更加优异。这主要得益于改进MS-RRT*算法将次根节点分布在整个地图环境之中，次根节点使用少量的取样节点对狭窄通道空间进行探索，同时，基于次根节点再选择的全局搜索策略，对全局地图中的狭窄通道探索，大大提高通过狭窄通道的概率。

4 结论

本文针对RRT*算法在狭窄通道搜索效率低、取样节点利用率不充分等局限性，设计了一种面向狭窄通道的多次根节点快速扩展随机树算法MS-RRT*。采用多个有限扩展次数的次根节点生成局部连通路径，同时通过不断重启和生成多个次根节点，找到狭窄通道区域，进而减少采样节点落在障碍物中的数量，提高通过狭窄通道的概率。

与传统的RRT*算法和Bi-RRT*算法以及Informed-RRT*算法进行对比实验，在多层狭窄通道环境下和含有多个障碍物的狭窄通道地图中，本文算法在在整个连通路径上取样节点的分布更加均衡，出现过度取样和欠缺取样的概率大大降低。在定量指标上，探索成功率、路径成本均值、首次探索到合适路径平均时间、取样节点落在障碍物中的数量、总耗费平均时间等性能指标也更加优异，通过狭窄通道的性能明显提高。