一种水声瞬态信号的下降沿检测方法

游 波，蔡志明

（1.武昌工学院电信与物联网工程系，湖北武汉 430065；2.海军工程大学电子工程学院水声工程系，湖北武汉 430033）

1 引言

水中声纳目标进行战术动作时会辐射瞬态信号.信号出现与消失时被检测序列概率密度函数（Probability Density Function，PDF）的变化是其统计特性的基本变化，累积和检测方法能够利用该变化进行有效的信号检测.在主动声纳检测方面，累积和检测后置处理利用匹配滤波的脉压效应将检测问题转化为瞬态信号检测问题，依据脉冲出现前后概率密度特性的变化来实现检测［1，2］.在被动检测方面，由于水声瞬态信号未知结构、未知长度、未知到达时间［3］和未知PDF模型等问题，检测难度大于主动声纳.变门限累积和方法［4］解决了未知长度瞬态信号的上升沿检测稳健性问题，用非高斯模型t分布假设［5］作为描述瞬态信号的PDF形式也进一步提高了上升沿的检测性能.实际上，下降沿出现时被检测序列PDF的变化与上升沿相反，检验统计量、门限等检测参数需要重新推导计算.原有累积和序贯检测理论假设将0作为下降沿的判别门限，会带来较大的检测误差，工程上采用的基于检验统计量均值和方差连续变化趋势的下降沿判断方法，需要反复调整经验系数，精确度并不高.

低信噪比情况下瞬态信号检测常采用基于变换域思想的方法，如基于高阶谱的Power-law检测器［6，7］、倒三谱［8］、短时傅里叶变换、Winger-Vill分布、小波变换、经验模态分解（Empirical Mode Decomposition，EMD）等.常规傅氏变换不能兼顾时间和频率分辨率的要求，小波变换基函数的选择对信号检测分析结果有较大影响，基于EMD分解方法［9，10］能将本地干扰和信号分解到不同固有模态函数中，去除干扰后的重构信号能提高检测性能.有规瞬态信号的EMD分解是有效的，但对于比如鱼雷出管这样由宽频噪声填充的无规瞬态信号，EMD分解反而会增加模态混叠程度，效果并不理想.累积和检测方法另辟蹊径，依据瞬态信号出现与消失时PDF的变化进行检测，因而建立PDF模型是关键环节.区分上升沿和下降沿被检测序列PDF变化，重新构建下降沿的累积和检测过程，提高下降沿检测精度，对于获取瞬态信号清晰的时频结构、进行有效的瞬态信号分类识别和作出及时的战术判断有着十分重要意义.

2 检验统计量推导

考虑到水声瞬态信号的突发性和不稳定性、声信道传播特性未知等因素，在一般意义上将声纳接收机输入信号中的瞬态变化视作方差发生变化的高斯分布［11］.给定独立观测值序列X={x1，x2，…，xn}，n为被检测序列长度.假设瞬态信号结束时，概率分布律从f0变化至f1，变化发生点θ未知，即：

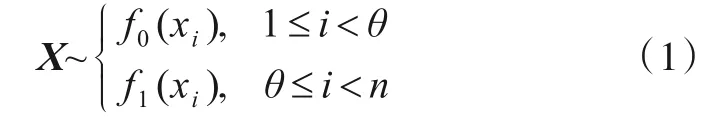
式中f0(xi)=N(0，σ2)表示在H0假设（信号未结束）下被检测序列服从均值为零、方差σ2的分布；通过对背景零均值化和功率归一化处理，可将H1假设下（信号结束）背景噪声的PDF分布设为f1(xi)=N(0，1).备择假设｛H1：θ=ν(ν＜n)｝对原假设｛H0：θ=∞（无变点）｝的对数似然比统计量［12］为：

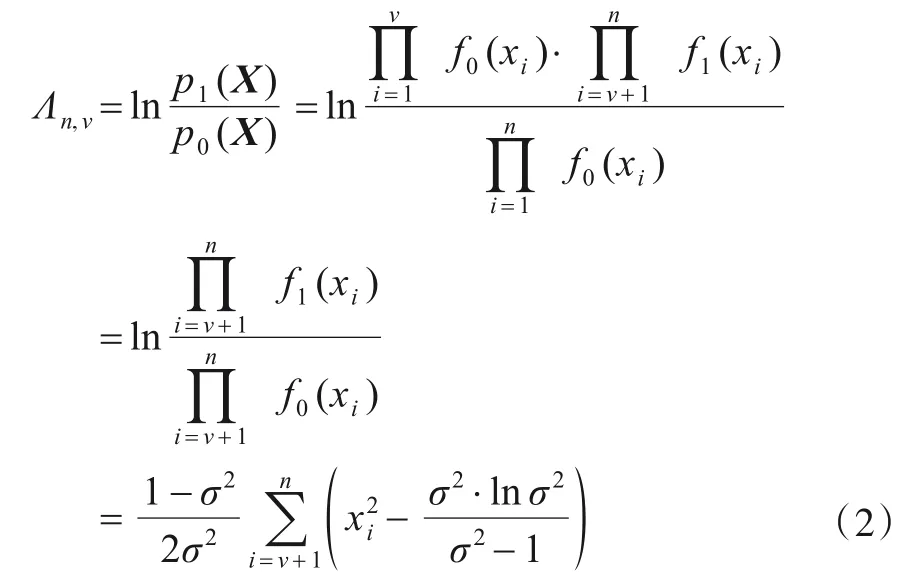
式（2）中p1(X)表示H1假设下检验统计量X的多点联合PDF，其中变点发生在i=ν的位置.p0(X)表示H0假设下X的PDF分布.令b=σ2·lnσ2/(σ2-1)为偏差，则对数似然比可写成：

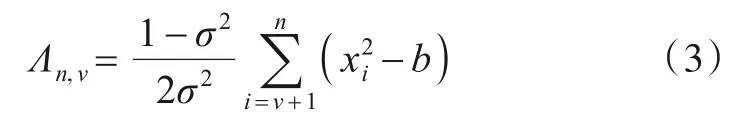
由于σ2为变化发生前瞬态信号加噪声的总方差，因此σ2＞1，(1-σ2)/2σ2＜0.依据最大似然比准则，对数似然比统计量等价于下述统计量：

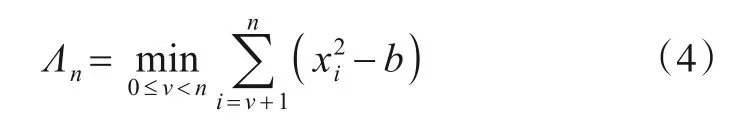
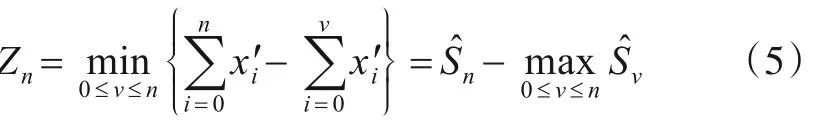
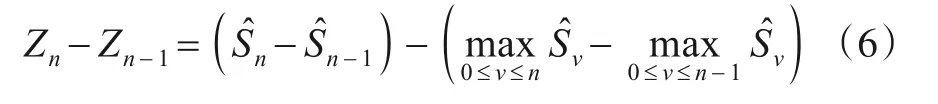
由于

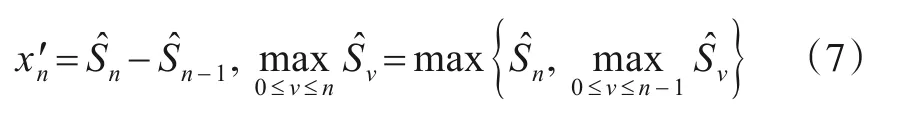
则

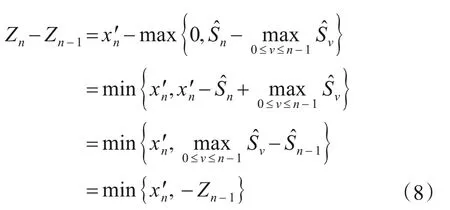
所以，Zn可递推实现，即得到下降沿检测完整的检验统计量：

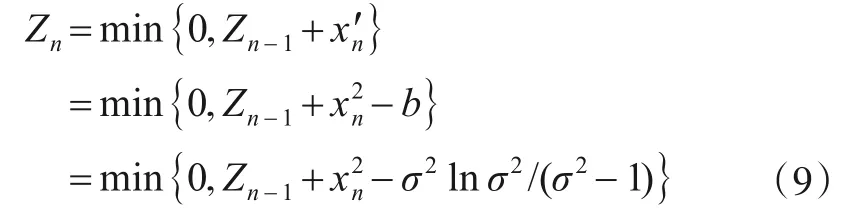
定义检测器非线性量或更新量为yn=g(xn)=x2nb=x2n-σ2lnσ2/(σ2-1)，是被检测序列X的函数.根据雅可比行列式，可得更新量的概率分布密度PDF：

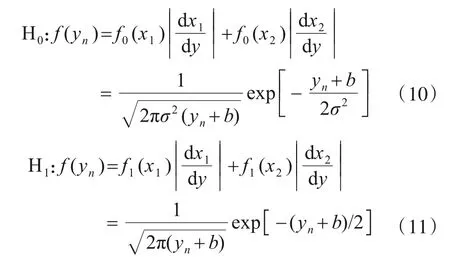
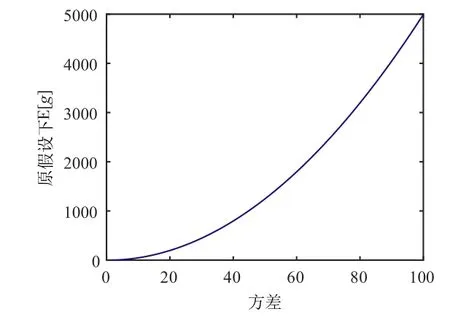
图1 原假设下E[g]随方差σ2的变化关系

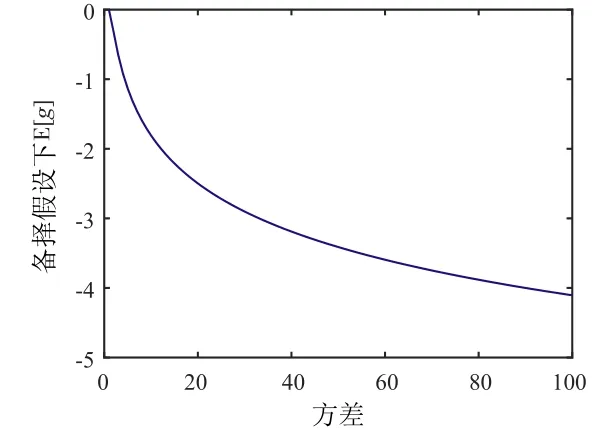
图2 备择假设下E[g]随方差σ2的变化关系

常规累积和上升沿检测理论模型可描述为序贯检测［4，5］：

式（13）中0和h分别设为上、下门限，显然将下降沿的检测门限简单设为0是不合适的，应根据本节的结论重新推导和计算.完整的累积和瞬态检测过程应包括上升沿和下降沿的同时检测，是两者的结合.

3 检测参数计算

3.1 下降沿检测性能分析模型

下面分析在序贯检测三种状态下（如式12）第n时刻检验统计量Zn的概率，再进行N步状态转移和递推，得到检测概率和虚警概率的数学表达.该分析模型为后续基于纽曼-皮尔逊准则，在给定检测和虚警概率条件下推算门限提供理论基础.该过程分析步骤与上升沿性能分析模型类似，下面重点给出下降沿分析模型的不同点.

关注具体的累积过程：Zn=Zn-1+g(xn)，n时刻检验统计量Zn的概率分布律等于n-1时刻Zn在范围(h，0)间的概率分布律fn-1(z)与更新量g(xn)概率分布律fg(z)的卷积［13，14］：

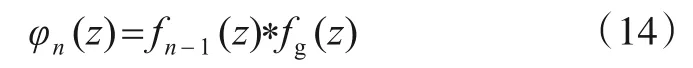
比较式（12）和式（13）可见，在推算三种状态下检验统计量Zn的概率时，下降沿检验统计量Zn的范围与上升沿显著不同.定义π0(n)表示未检测到下降沿的概率：

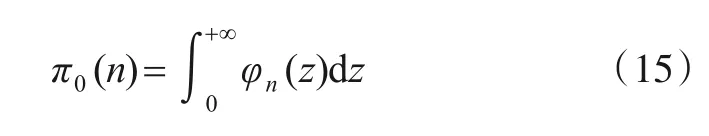
定义π1(n)表示在上述条件下在时刻n结束且检测结果为检测到下降沿的概率：

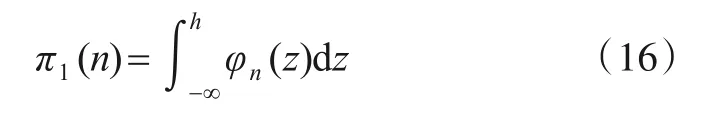
定义π2(n)表示检测过程能持续到下一个时刻的概率，即检验统计量Zn在范围(h，0)间的概率：

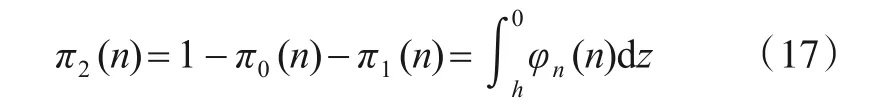
对结果进行归一化处理，一次检测过程持续到n时刻检验统计量Zn在范围(h，0)间的概率分布密度fn(z)表为：

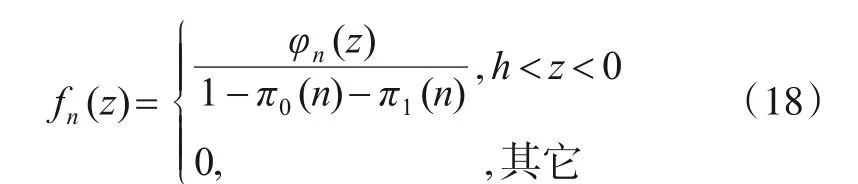
接下来的思路与上升沿检测类似［13，14］，由式（14）～（18）对累积过程进行状态递推，可得在n时刻之前未过门限或置零复位的假设下，检测持续到时刻n+1的概率pon(n)=pon(n-1)π2(n)、持续到n时刻并判为未检测到下降沿的概率p0(n)=pon(n-1)π0(n)、在n时刻结束且检测到下降沿的概率p1(n)=pon(n-1)π1(n).

下降沿检测包括正常检测和延迟检测两部分之和［13，14］，但与上升沿检测不同的是，正常检测是指初始检测状态为检验统计量进入稳态（即瞬态信号已经发生，H0假设），在H1假设下低于检测门限，此时不必考虑0初始状态的情形.延迟检测是指H0假设下进入稳态，在H1假设下未低于门限，但在重新转换成H0假设时低于门限的情形.检测概率可表为：

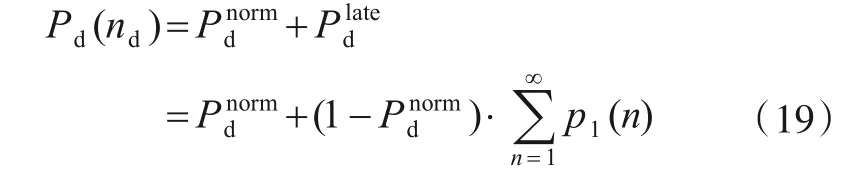
式中p1(n)为H0假设下持续到n时刻，检测到下降沿的概率.正常检测概率Pdnorm包括初始状态为稳态时未经置零低于门限和经过k次置零低于门限的概率之和［14］：

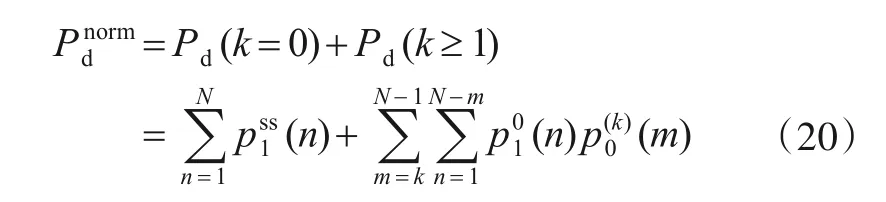
式中ps1s(n)表示H0假设下稳定初始状态为fss(z)时检验过程一直持续到n时刻检测判决为下降沿（记为1）的概率，N为被检测序列的长度.p(0k)(m)为k次置零复位（未检测到下降沿，记为0）的概率.p01(n)表示剩余(N-m)个序列点从0状态开始，检测到下降沿，记为1的概率.H0假设下进入稳态时检验统计量Zn的概率密度函数［14］表为：

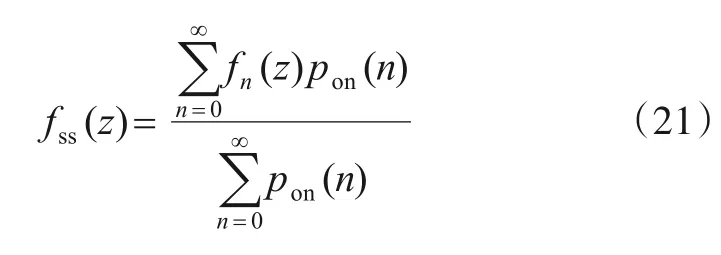
对累积过程进行状态递推的基础是对更新量g(xn)进行量化，根据式（10）、式（11）更新量的PDF构建马尔科夫状态转移矩阵，这是进行虚警概率和检测概率推算的必要条件，具体过程详见之前的工作［14］.虚警概率的计算考虑在H0假设下低于检测门限的概率，详细过程不再赘述.

3.2 检测参数的计算结果

前两节性能分析模型给出了基于状态递推的检测和虚警概率的计算过程，反过来，根据纽曼皮尔逊准则，在方差变化高斯分布的PDF假设，如式（1），在满足虚警概率Pfa=10-4和检测概率Pd=0.6条件下，可以反推累积和方法的门限h和方差σ2等检测参数.根据其随瞬态变化长度N的变化规律，计算搜索过程可以进行优化，结果如图3和图4所示.

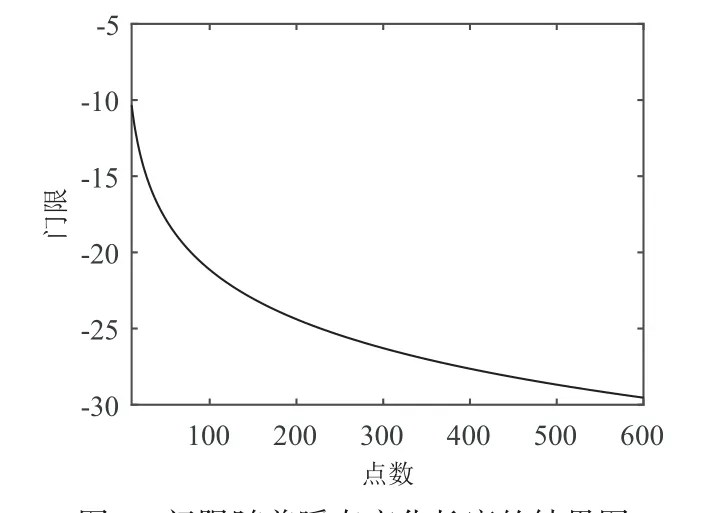
图3 门限随着瞬态变化长度的结果图

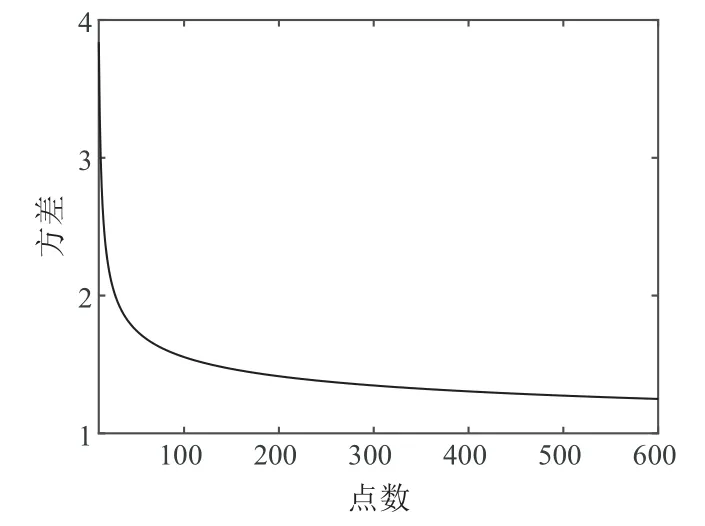
图4 方差随着瞬态变化长度的结果图

4 数据验证

在工程实现上，常规累积和检验方法的下降沿检测是从当前时刻开始，将检验统计量以L为长度分成M段，分别计算每段数据的方差V(xi)和均值J(xi)，i=1～M.如果出现M段V(xi)的增大或者J(xi)的连续下降，即判为信号下降沿.M和L与采样率、信噪比和瞬态信号特征有关，均为经验值，检测稳健性较差.本文三个例子信号采样率fs=1000 Hz，M=50，L=5.下面利用常规方法和改进方法对舰船转舵仿真信号、鱼雷出管仿真信号和水池重物落水实测信号进行下降沿检测分析比较.

4.1 舰船转舵信号仿真和检测结果

舰船转舵辐射噪声主要由机械撞击和空化气泡破灭噪声组成.仿真信号模型采用多个起始时间不同的指数衰减正弦信号之和，同组合高斯包络信号的叠加来表示，表达为［15］：

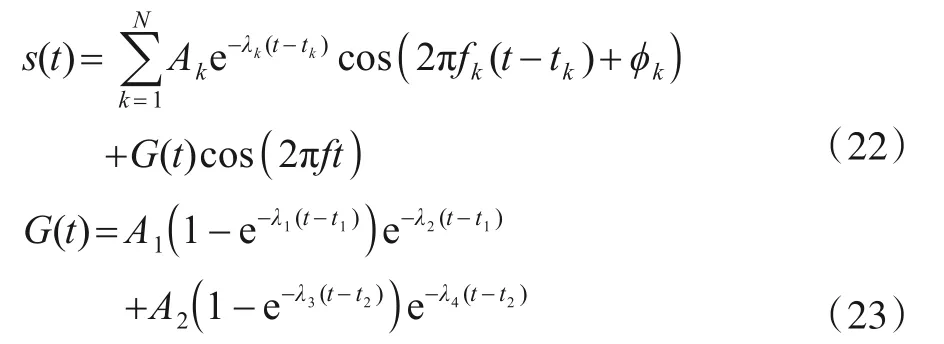
式中G(t)为组合高斯包络，设N=5，正弦信号幅度A1=A2=A4=0.23，A3=0.25，A5=0.08，指数衰减系数λ1=0，λ2=λ4=3.3，λ3=1.96，λ5=5.2，正 弦 信 号 频 率f1=f4=150 Hz，f2=f3=120 Hz，f=50 Hz，f5=100 Hz，初相φk=0.仿真波形如图5所示，时长1 s，采样率为1000 Hz.

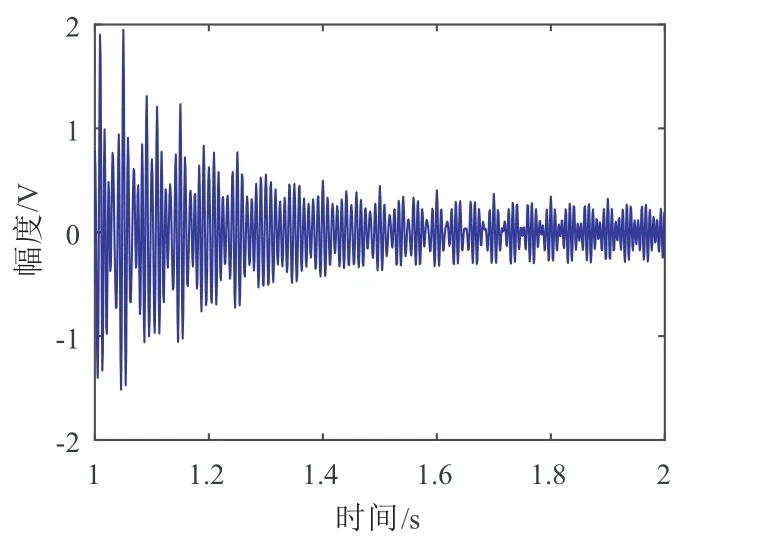
图5 转舵仿真信号

将信号以3 dB的信噪比叠加到高斯白噪声背景1s处，2 s处信号结束，如图6所示.转舵信号由强变弱，在信噪比变弱时常规累积和下降沿判定误差较大，判为1.792 s，而新方法判定结果为2.034 s，绝对误差为0.034 s，精度更高.表1为不同信噪比下进行1000次蒙特卡洛实验得到的两种方法平均绝对误差，新方法下降沿检测误差有明显下降.

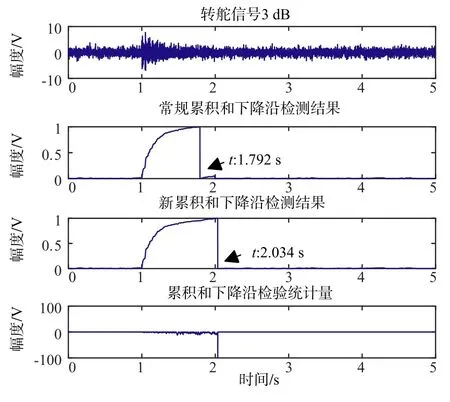
图6 转舵仿真信号下降沿检测效果比对

表1 不同信噪比下1000次蒙特卡洛实验两种方法平均绝对误差

4.2 鱼雷出管信号仿真和检测结果

鱼雷发射过程中的瞬态信号［16］主要包括三部分，盖板声、出管声和启动点火声.盖板声是在发射管与海水保持连通后，前盖板开启过程中产生的机械冲击类信号.采用包络加权的多次谐波敲击瞬态信号进行模拟，压缩空气膨胀将鱼雷推出管的信号采用指数衰减包络加权的带限噪声进行模拟，启动点火信号为燃料点火燃烧和螺旋桨运动的噪声，采用对数调频和均匀分布的宽带填充噪声复合构成，该噪声相比前两者信噪比更大，并且热动力雷和电动力雷的启动点火噪声特性不同，因而本文针对前两部分相对比较弱的噪声进行仿真和检测.

多次谐波敲击瞬态信号的包络设为上升沿陡、下降沿缓的形状，可表为［16］：

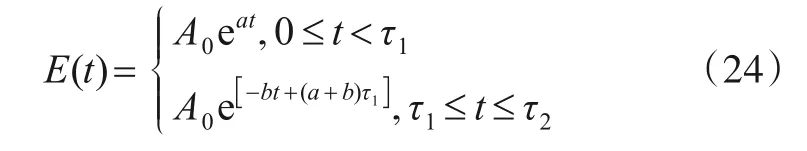
式中A0为幅度，τ1和τ2为信号上升时刻和信号持续时间，仿真中τ1=0.2s，τ2=0.6s，a=1，b=0.5.被调制的是以平台自身固有频率为主、含有多次谐波分量的信号，可表为：

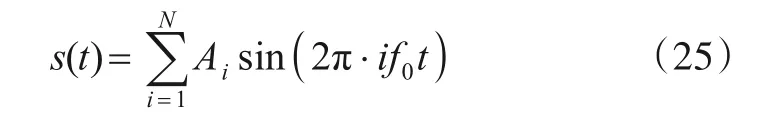
式中Ai为对应谐波信号幅度，N为谐波次数.取基频为f0=100 Hz，谐波幅度分别为1、0.4、0.2、0.1.鱼雷出管仿真结果如图7所示，盖板声时长0.6 s，出管信号时长0.8 s，分别在1 s和3 s处以-3.7 dB和-3.5 dB的信噪比叠加到高斯白噪声N(0，1)上，真实下降沿分别为1.6 s和3.8 s.检测效果比对如图8所示.可见当瞬态信号信噪比较低时，常规下降沿检测易受到随机噪声的干扰，出现误判，出现多次下降沿.而新下降沿检测算法的检测结果更加准确，绝对误差为0.028 s和0.029 s.表2为不同信噪比下进行1000次蒙特卡洛实验得到的两种方法平均绝对误差，可见新方法对盖板声和出管声下降沿检测精度更高.

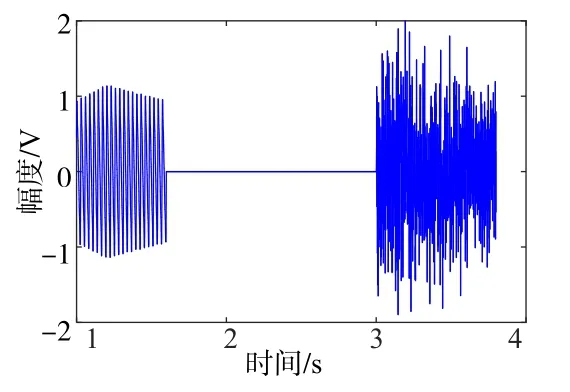
图7 鱼雷出管信号仿真

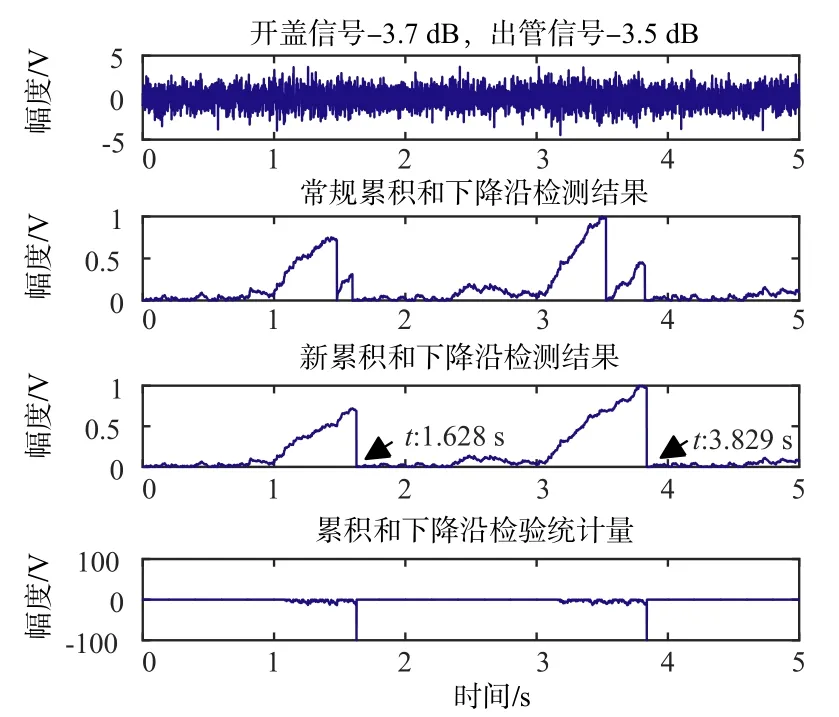
图8 鱼雷出管信号下降沿检测效果比对

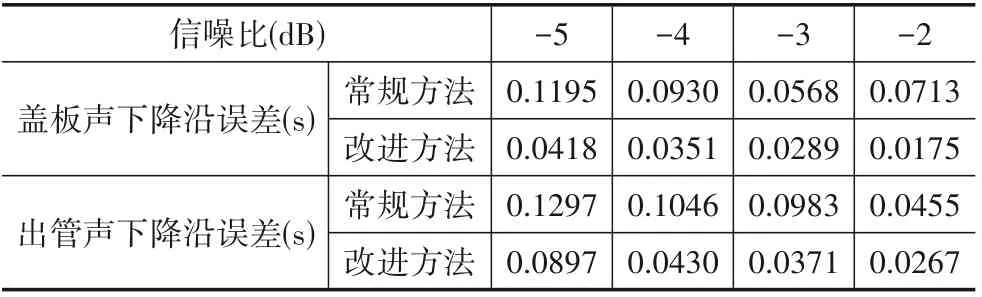
表2 不同信噪比下1000次蒙特卡洛实验两种方法平均绝对误差

4.3 水池数据验证

将重物小铁锤在2 m高度自由落入消声水池，由于重物体积小，击水声弱，故采集的信号主要为脉动声，如图9所示.信号时长4 s，疏样后的采样率1000 Hz，主要频率范围为100～210 Hz，带通滤波频段［50 Hz，300 Hz］，以-5 dB信噪比添加到带限高斯白噪声上，如图10上图所示.进行零均值化和背景噪声功率归一化处理，常规和改进下降沿的检测结果如图10中图所示.依据均值和方差变化的常规方法在脉动信号信噪比逐渐减弱时出现较大的下降沿检测误差，精度明显低于新方法.常规方法检测到的信号下降沿为2.557 s，改进方法检测到的信号下降沿为2.855 s.事实上信号的主要能量约分布在2.1 s至2.8 s的时间段，可见改进方法精度更高，稳健性更好.图11为不同信噪比下进行1000次蒙特卡洛实验得到的两种方法平均绝对误差对比，可见随着信噪比的降低，相对于常规方法，新方法对重物落水信号下降沿检测误差更小.

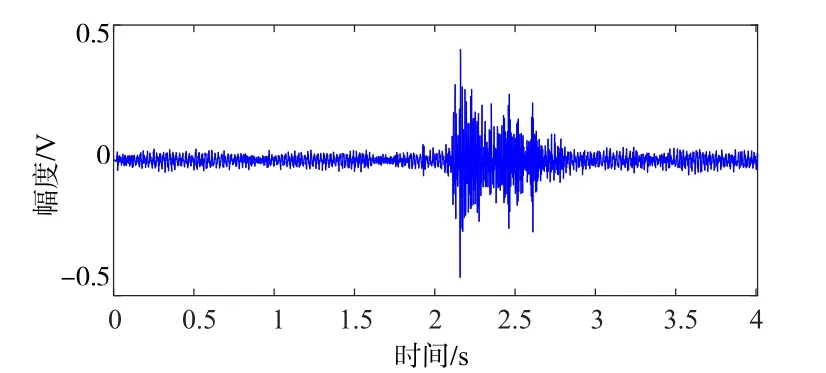
图9 水池重物落水脉动信号

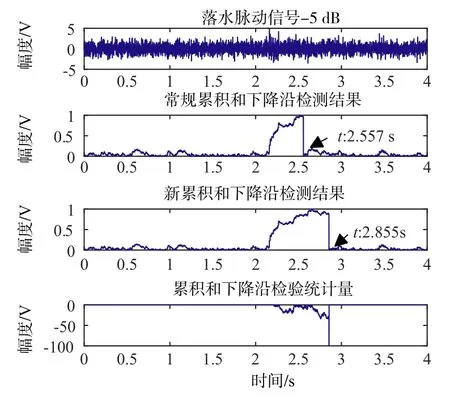
图10 水池重物落水信号下降沿检测效果比对

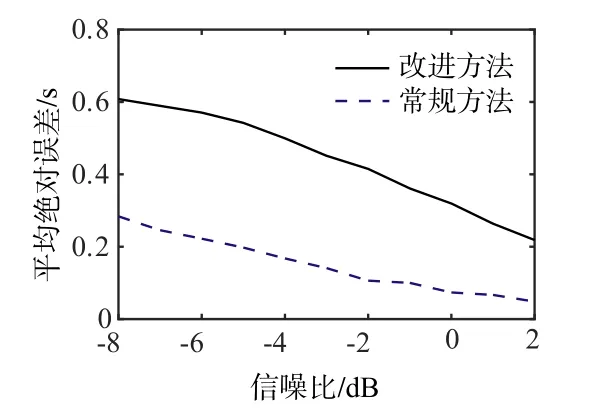
图11 不同信噪比下1000次蒙特卡洛实验两种方法平均绝对误差对比

5 小结

在利用累积和算法对瞬态信号上升沿检测的基础上，本文依据信号结束时PDF的变化重新推导了检验统计量和更新量的概率密度函数表达；在性能分析模型方面，仍然利用FFT方法，但严格区分了上升沿检测和下降沿检测的不同，推导了检测概率的计算公式；依据纽曼皮尔逊准则计算了在虚警概率Pfa=10-4和检测概率Pd=0.6条件下，方差变化高斯过程假设下的检测参数.舰船转舵仿真信号、鱼雷出管仿真信号和水池重物落水实测脉动信号的验证结果表明，低信噪比下，新方法对瞬态信号下降沿的判断精确度更高，稳健性更好.