基于易损性分析的特种设备结构体系研究

王全伟，文豪，徐格宁，孟文俊

（太原科技大学机械工程学院，山西 太原 030024）

特种设备具有高能量积聚、高危险性作业等特点。截至2020年底，全国仅起重机械就达253.84万台［1］，结构失效事故约占全国特种设备事故总起数一半以上。

特种设备的大型化常常表现为庞大的结构尺度［2］，结构在长期使用中因其材料自身的性能退化损伤导致结构坍塌的事故频发［3］，而仅通过增大构件安全裕度、控制加工工艺质量、加强制造监督等方法，并不足以彻底解决结构安全问题，仍须考虑结构整体可能存在的连续失效机制，即易损性。

易损性分析起源于军事工程领域，后逐步应用于建筑［4］和桥梁［5］工程。1973年，Whimtann等［6］在建筑结构最先提出采用离散型破坏概率矩阵描述不同类型建筑结构的地震易损性。2000年，Shinozuka等［7］结合实际桥梁震灾首次提出以极大似然法估计的双参数对数正态分布模型建立易损性曲线。杨毅等［8］率先从地震破坏等级和性能水平，以结构位移角给出一种岸桥结构性能水准的确定方法。

在设备结构健康监测中，为获得最佳的监测效果，常将传感元件布置在结构响应较大的测点处，造成传感元件布设数量大而集中，导致检测成本增加、数据海量冗余、维护保养不便等一系列难题。因此，如何有效捕捉结构易损伤的关键区域决定了结构健康监测的效果。

本文拟从易损性概念及原理入手，结合特种设备特定机型结构，将易损性分析应用于设备结构健康监测的具体工程实践，进行论证和研究。

1 结构易损性基本概念

结构的易损性是指结构容易受到伤害或损伤的程度，反映了特定条件下结构的脆弱性和结构对意外损伤的承受能力，主要表现在连续性破坏与倒塌事故中，即结构由于荷载作用产生局部破坏，进而造成相邻连接构件发生连续破坏，最终导致结构发生局部或整体倒塌［9］。目前，国内外易损性分析方法主要有经验分析法、数值解析法、实验模拟法等［4-5］。经验分析法多依靠主观因素较多的专家经验或规范规定；实验模拟法可信度较高，但需要模拟真实破坏条件；数值解析法结合理论模型并同时兼顾定量计算和定性分析，并可引入多项不确定因素，故被多数专家学者认可和广泛采用。

2 相关易损性分析理论

2.1 重要性系数和冗余度

机电类特种设备的结构体系的构造型式以格构式的桁架二力杆系和实腹式的箱型梁柱为主。结构体系（桁架或刚架）可视为不同构件的组合，当考虑构件刚度的抗破坏失效能力时，可采用基于刚度的重要性系数方法来反映构件重要程度。

任意构件i的重要性系数γi［9］为

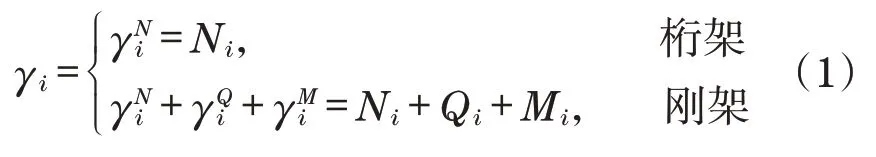
式中：构件i两端施加单位平衡力系后，对于桁架体系，Ni为杆件轴力（拉力/压力）；对于刚架体系，Ni、Qi、Mi为杆系轴力、剪力、弯矩；ri为构件i的冗余度，力系单位进行了无量纲化处理。

构件重要性系数γi与冗余度r的关系：

式中：n为结构的构件数。

通过构建节点位移向量到构件实际变形量的转换矩阵A，并以杆系内力构建变形刚度矩阵K，通过公式变换得到结构转换矩阵B=A（ATKA）-1ATK，由此得到各构件的重要性系数和冗余度。

2.2 失效模式和失效路径

通过移除具有最小冗余度的构件，将剩余结构作为新的平衡体系进行静不定动不定分析［10］，根据分析条件判定结构存在的失效模式和失效路径。

若总构件数为b，节点数为n，约束数为c，则非约束节点位移数为（3n-c），平衡方程为

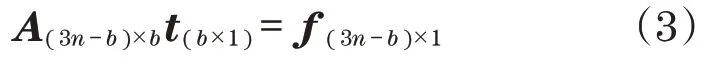
式中：A（3n-c）×b为结构平衡矩阵；tb×1为构件内力向量；f（3n-c）×1为节点载荷向量。

若用r表示平衡矩阵A的秩，则结构自应力模态数u和机构位移模态数v分别为

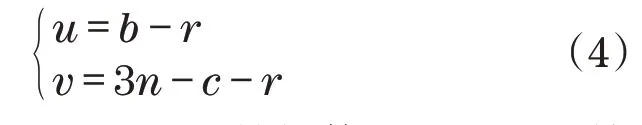
当且仅当u≥0、v＞0时，结构体系是不能再持续承受载荷的静不定动不定体系，可判定结构失效并形成某条固定的失效路径；否则，移除剩余平衡体系中的最小冗余度构件，形成新的结构平衡体系持续进行失效分析并判定，直至判定失效。失效路径总体表现为结构体系中构件发生破坏或失效后的能量传递关系，以应变和应力形式贮存在物体中的势能（应变能［11］）U来体现能量需求：

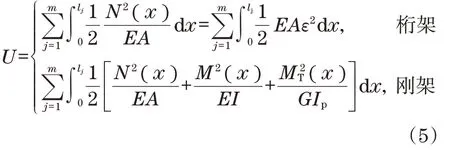
式中：m为失效路径中的总构件数；lj为第j个构件的长度；对于桁架体系，EA为抗拉压刚度，ε为材料应变；对于刚架体系，EA、EI、GIp分别为抗拉压刚度、弯曲刚度、抗扭刚度。

2.3 能量流动势和损伤指标

结构体系的构件在载荷作用下内部将产生能量流动场（矢量），能量流动方向（势高→势低）为流动势［12］，构件任意截面（a、b）的流动势ΔPab为

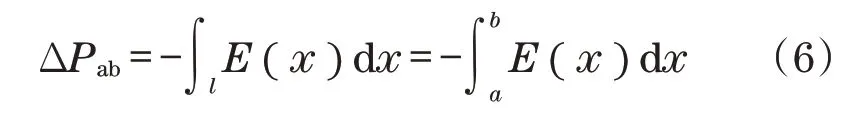
式中：E（x）为构件截面的能量流动；l为构件的长度。

由于结构体系中内在能量的流动过程中会转化为应变能，根据流动势分布及应变能密度为基础，可建立结构整体的损伤指标γF：

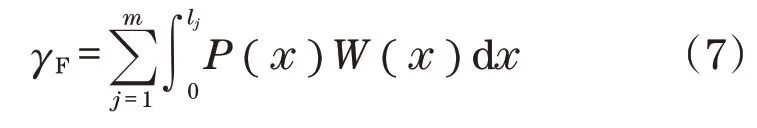
式中：P（x）为构件流动势；W（x）为构件应变能密度。

3 基于易损性分析的结构健康监测技术

设备结构健康监测技术的传感系统最优布设设计方案主要分为易损性计算、分析、判定3个模块，以此评估结构体系的最易损关键区域，并将该位置作为传感系统的最佳布设区域，分析流程如图1所示。

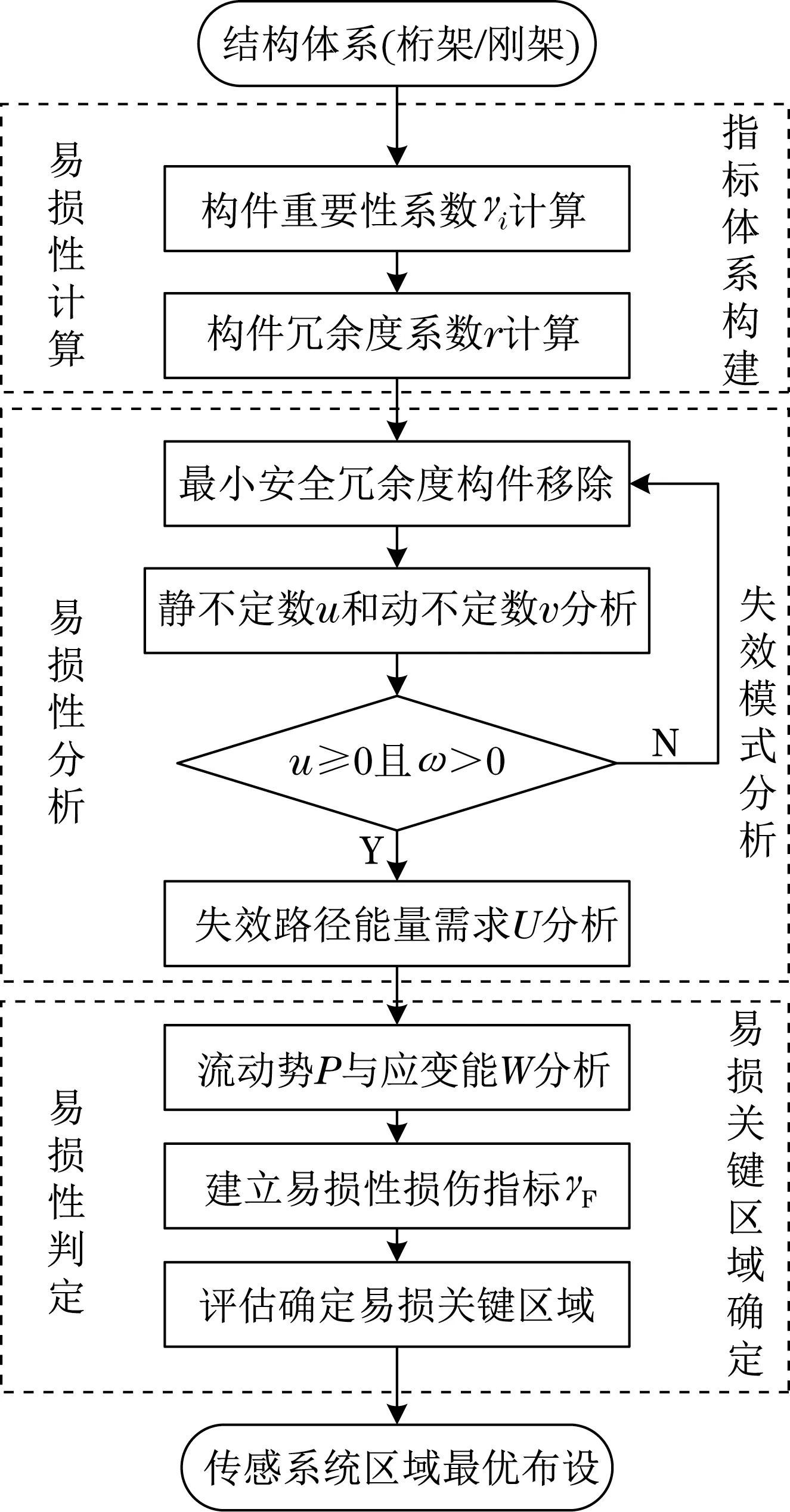
图1 传感系统最优布设方案流程Fig.1 Flow chart of optimal layout of sensor system

4 典型案例分析

4.1 桁架结构体系

1）模型基本介绍。某桁架式金属结构主梁，由角钢和工字钢构成，基本模型如图2所示。

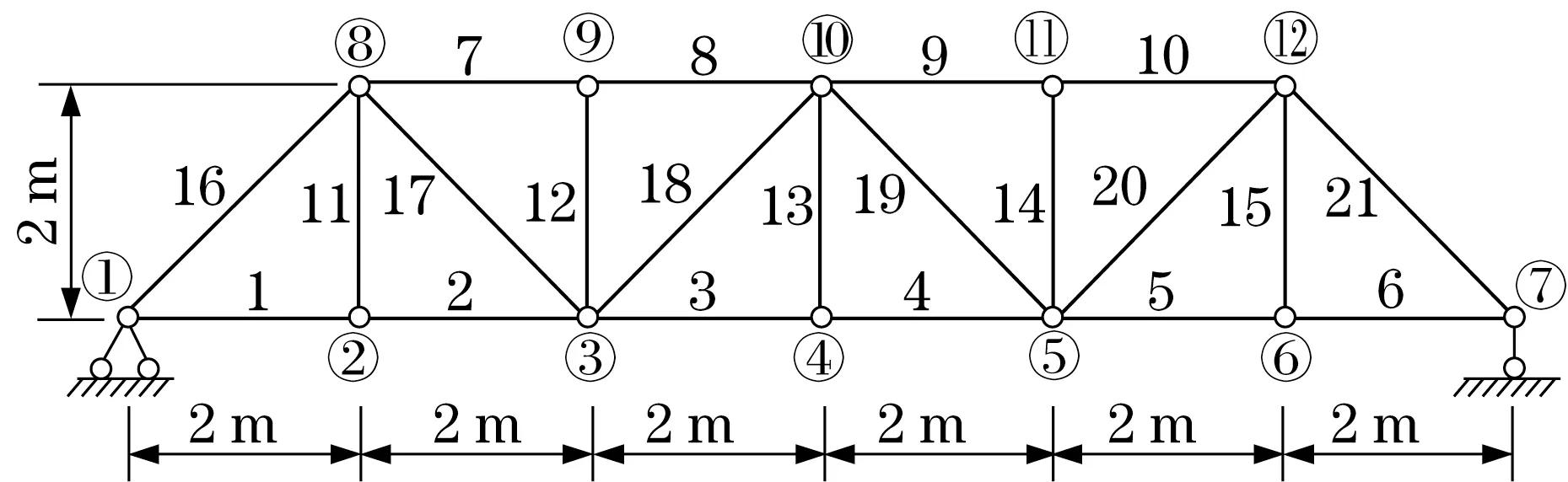
图2 桁架结构模型Fig.2 Truss structure model

2）构件系数计算。通过B=A（ATKA）-1ATK变换公式，得到各构件的重要性系数和冗余度，见表1。

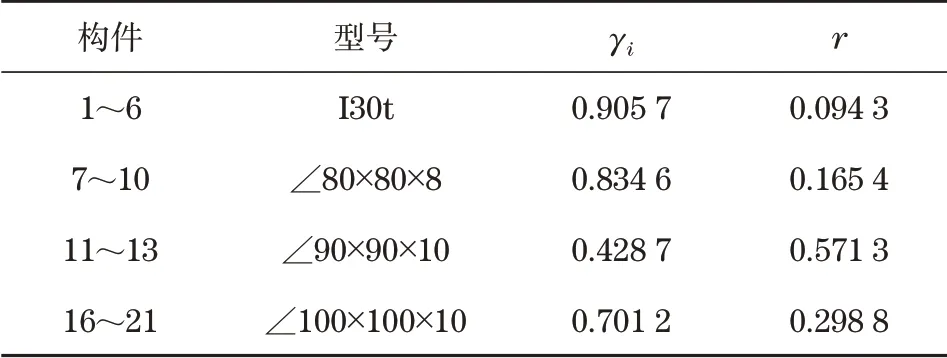
表1 构件重要性系数和冗余度Tab.1 Component importance coefficient and redundancy

3）失效模式分析。依据桁架结构体系失效模式分析，经过判定得到4条失效路径，见表2。

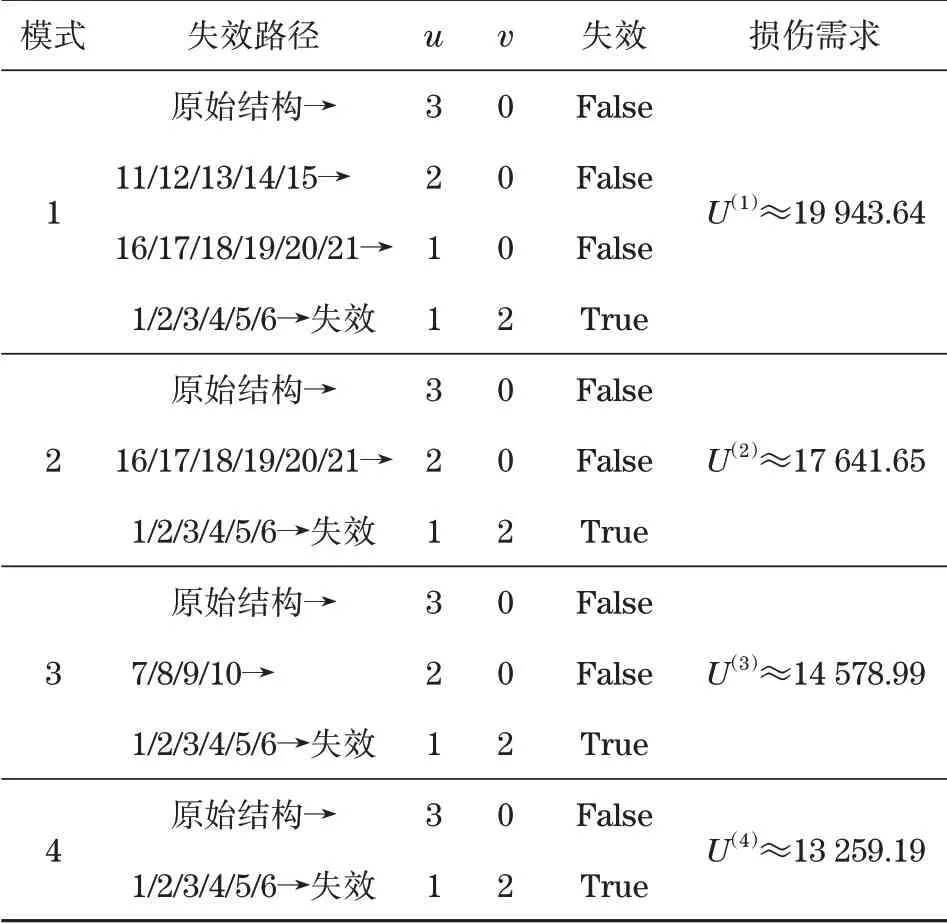
表2 失效模式分析与判定Tab.2 Analysis and identification of failure modes

失效模式4为最易损失效路径。

4）结构能量流动及流动势分析。在构件相应节点位置施加端梁q1（10 kN）、主梁q2（20 kN）、移动小车和吊重p（55 kN）载荷，结构损伤指标如图3所示。

尽管戈尔巴乔夫为消除改革阻力与疏通改革之路采取了一系列措施，但是，经济体制改革最后仍然没有取得成功，这是因为戈尔巴乔夫在改革过程存在不少严重的失误。

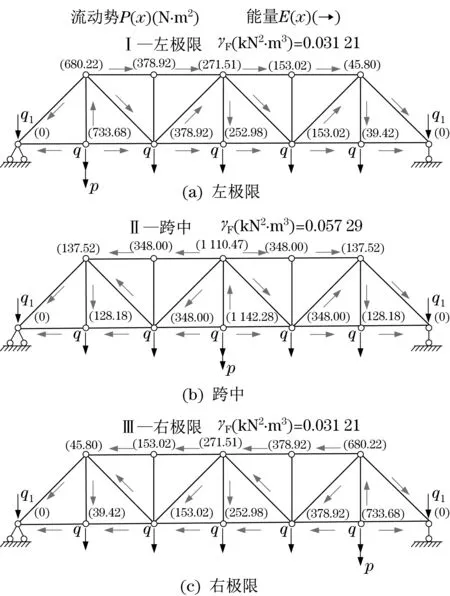
图3 桁架结构在不同载荷工况位置时的易损性指标Fig.3 Fragility of truss under different load conditions

4.2 刚架结构体系

1）模型基本介绍。某铸造起重机采用箱型截面的主梁和端梁结构，单侧两根端梁之间采用中间连接梁铰接，模型如图4所示，截面尺寸如图5所示。

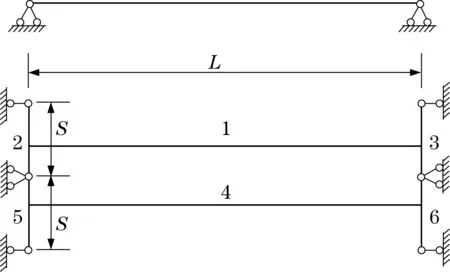
图4 刚架结构简化模型Fig.4 Simplified model of bridge structure

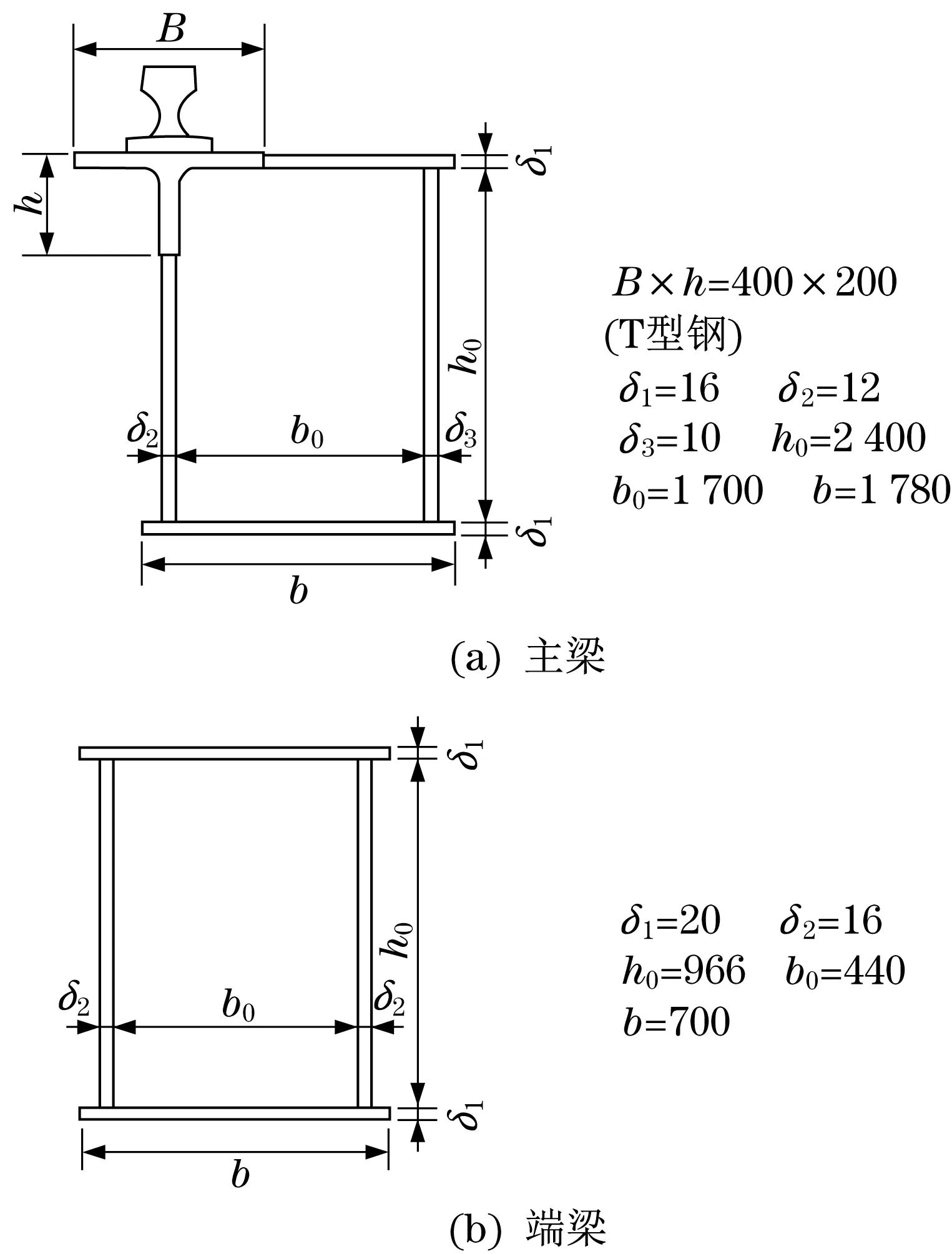
图5 铸造起重机尺寸参数Fig.5 Dimension parameters of the casting crane

2）构件系数计算。通过B=A（ATKA）-1ATK，变换公式，得到各构件的重要性系数和冗余度，见表3。

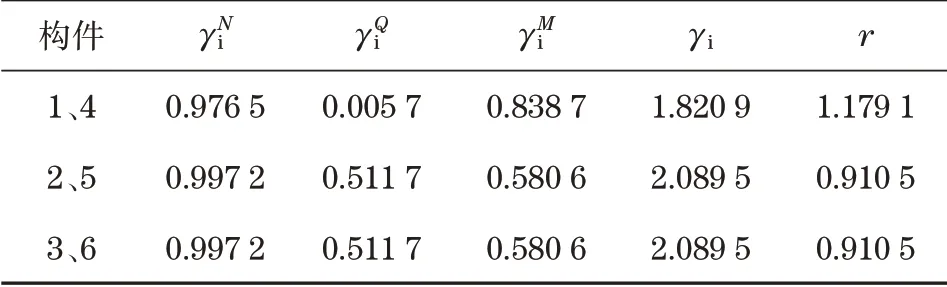
表3 构件重要性系数和冗余度Tab.3 Component importance coefficient and redundancy

3）失效模式分析。依据刚架结构体系失效模式分析，经过判定得到2条失效路径。失效路径1：1→2/3→失效破坏，U（1）≈492 770 J；失效路径2：2/3→失效破坏，U（2）≈63 198 J。结构体系最易损路径为失效路径2。

4）结构能量流动及流动势分析。在构件相应位置施加载荷，结构主梁自重为均布载荷q（x），移动小车和吊重为集中载荷p（A和B），如图6所示。

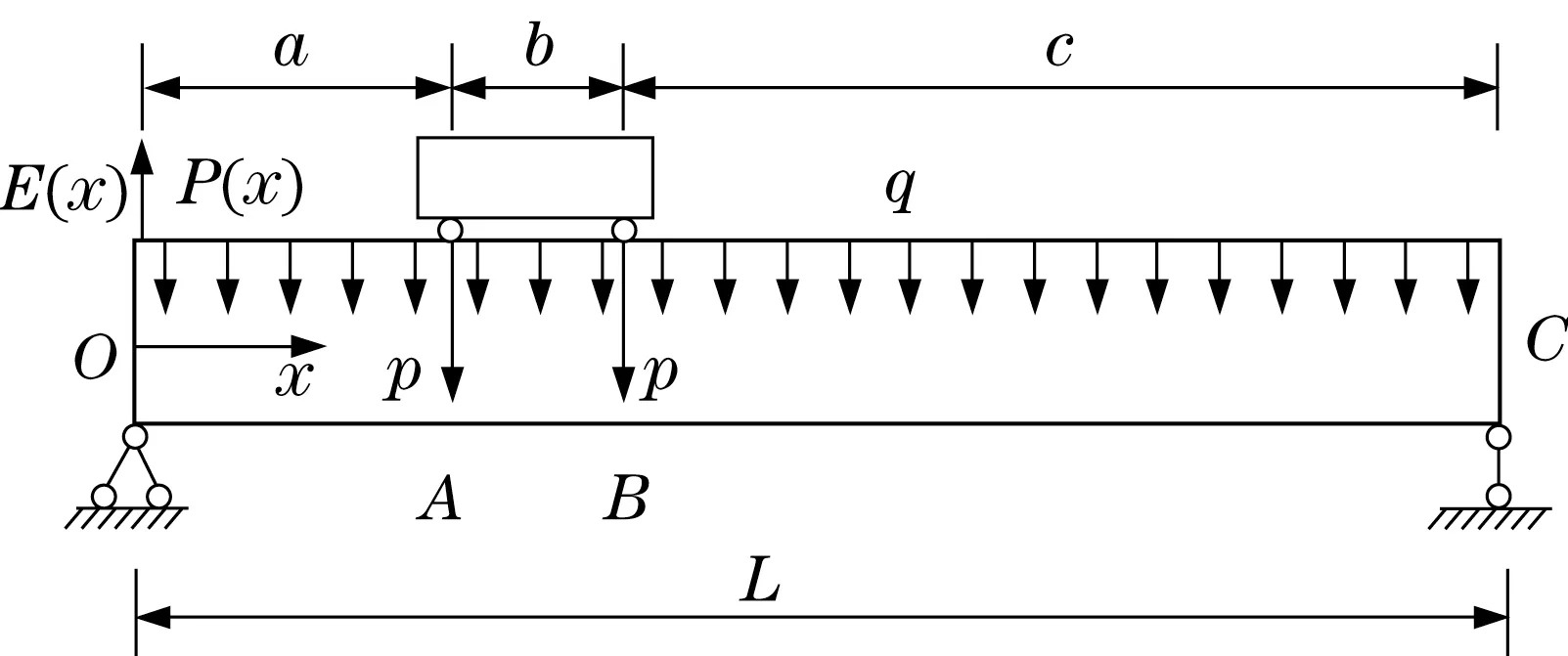
图6 结构主梁力学模型Fig.6 Mechanical model of main beam

为便于计算，建立坐标系记α=x/L，α∈［-0.5，0.5］，结构损伤指标如图7所示。

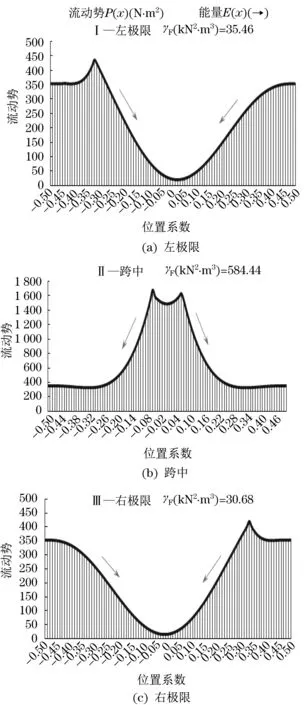
图7 刚架结构在不同载荷工况位置时的易损性指标Fig.7 Fragility index of rigid under different load conditions

4.3 讨论分析

桁架结构体系中，γi的排序为：下弦杆＞上弦杆＞斜杆＞竖杆；下弦杆同时承受自重和移动载荷，因其无可替代传力构件，如失效必将引起整体失效；竖杆所受的内力较小，局部构件甚至为零杆，因存在可替代传力构件（斜杆），如失效并不会导致整体失效；上弦杆和斜杆发生失效时情况类似。

刚架结构体系中，主梁的γi低于端梁，符合“强柱弱梁”的设计思想；主梁的轴向γiN略低于端梁，剪切γiQ明显低于端梁，弯曲γiM则明显高于端梁，体现了“主梁承弯端梁承剪”的主要功能。

当起重小车作用于跨中时，能量流动传递形式表现为跨中分布较大而两侧较小，说明在跨中载荷作用力较大则弯曲变形较大，吸收较多的外力作用能量，从而对结构体系的能量流动影响也较大，易损指标γF相对较大。

从易损性总体指标的特征分析，跨中作用工况的易损性指标明显高于两侧极限位置，说明吊重载荷较大引起的能量集中，也使得主梁的跨中区域更易受损（即能量吸收最多区域）。

5 结语

针对特种设备结构体系，采用重要性和冗余度系数、静不定动不定、能量流动势等易损性分析方法，构建结构关键区域的损伤指标，可评估结构体系的最易损关键区域，并将此薄弱环节作为设备结构健康监测传感系统的重点布设区域，为工程实践提供参考。