脆性岩石多裂缝干扰扩展机理研究

钟 权，罗攀登，罗天雨

（1.中国石油化工股份有限公司西北油田分公司，新疆 乌鲁木齐 830011；2.广东石油化工学院，广东 茂名 525023）

我国有着辽阔的海域，在东海区域、渤海区域和南海区域都有着丰富的石油及天然气储备[1]，加速对海洋油气资源的开发，对实现我国经济可持续发展具有重大保障[2-3]。

据测算，南海北部湾海域涠西南凹陷页岩油资源量达8 亿吨，整个北部湾盆地页岩油资源量约12亿吨，展现了良好的勘探前景[4]。海下页岩油与陆地页岩气，都属于非常规油气资源，具有非均质程度强、岩性变化大、低渗致密、存在天然微裂缝等特性。低渗透油田的开采一直是限制海洋油气资源行业发展的重要原因，突破技术瓶颈，加强对非常规油气资源开发技术的研究是海洋油气高效开发的途径[5-8]。

体积压裂技术[9-10]是开发非常规油气田的重要手段，它是指在水力压裂过程中，在地层中形成裂缝网络，使得油气渗流到裂缝和井筒的距离缩短，渗流阻力减小，从而提高油气产量。在页岩油、页岩气等类脆性岩石中发育多重天然微裂缝，天然裂缝的扩展对裂缝网络的形成起着制约作用[11-12]，而多裂缝岩体在不同应力作用下的宏观破坏规律至今未被很好揭示。因此对多裂缝岩体宏观断裂破坏规律进行研究，无论从理论上还是工程实际上都具有十分重要的意义。

岩石是一种结构非常复杂的固体材料，它是由多种胶结物、矿物晶粒和孔隙组成的混合体。岩石中存在的断层、节理和裂隙等缺陷对岩石力学性质有很大影响，岩石在各种应力（包括水力压裂）作用下形成裂缝网络的实质就是岩石中天然裂缝的开启、扩展、相互作用和贯通的过程，所以对岩石裂缝尖端的力学性质进行研究有很大的意义。传统的断裂力学研究的对象主要是3 种基本裂缝类型：张开型（Ⅰ型）、滑开型（Ⅱ型）和撕开型（Ⅲ型）。但实际结构中的受力是非常复杂的，使得裂缝尖端的应力场多为复合型，其中又以压剪复合型居多。国内外学者对裂缝的失稳研究取得了丰硕的成果，建立了相应的断裂准则，需要解决的核心问题是裂缝尖端的起裂（延伸）角度及在何种力学条件下起裂。目前比较常用的裂缝扩展准则主要有两类：①应力参数法：如最大周向应力理论[13]、Mises 准则、岩石压剪断裂判据Mohr-Coulumb 准则和Drucker-Prager 准则[14]、Hoke-Brown 准则[15-16]、最大拉应变[17]、径向剪应力准则[18]、双剪应力准则[18]等。②能量参数法：如应变能密度因子理论[19]、最大能量释放率理论[20]、复合型裂缝的应变能准则[21]、最小J2 准则[14，22-23]等。脆性破裂有剪切和张拉两种主要的破裂形式[24]。应变类准则在压剪Ⅰ-Ⅱ复合型断裂问题中给出的结果与岩石及类岩石材料的实验结果最为接近[17]。本文拟用最大周向拉应变理论，并在平面应变条件下对主裂缝周围的脆性岩石进行起裂分析。

由于压剪断裂问题的复杂性，还有许多问题需要进一步的研究。目前对于水力压裂主裂缝的破裂及扩展延展规律研究较多[25]，对于主裂缝形成过程中，主裂缝壁面上、主裂缝两侧岩体的水平切面上的天然裂缝在何种条件下破裂、如何扩展的规律，较少进行研究。而这种研究，对于水力压裂过程中裂缝网络的形成至关重要。同时，以往对压剪复合型断裂问题的研究，侧重于单裂缝断裂规律的研究，较少对多条裂缝同时存在条件下的裂缝扩展规律进行研究，应用断裂力学理论建立页岩沿层理面裂缝起裂扩展准则鲜有报道。通过实验可知，单裂缝体的承载能力显然会高于相同类型的多裂缝体，多裂缝体的应力强度因子有所提高[26-27]。在脆性地层中同时存在多裂缝的情况比较普遍，因此需要研究多个裂缝同时存在时裂缝的开启及扩展规律。在同一无限大平面板中，多个裂缝之间的关系可分为平行裂缝、非平行裂缝（相交裂缝、非相交同轴裂缝），其中非相交同轴裂缝随着裂缝的扩展延伸将会发展为相交裂缝。因此本研究着重研究同轴裂缝情形下的裂缝扩展规律。

1 多裂缝应力强度因子计算

本文旨在揭示在水力压裂过程中，主裂缝壁面上多个天然裂缝在压裂液压力的作用下的开启规律。引入以下假设：①认为所研究岩石属于脆性材料，并符合线弹性应变规律。对于页岩油、页岩气等，在一定条件下属于脆性材料；②材料各向同性；③天然裂缝为理想裂缝，裂缝尺寸远远小于岩体的尺寸，而岩体尺寸为无限大；④不计体力；⑤裂缝为穿透型。

在水力压裂过程中，已经开启了垂直主裂缝，在主裂缝壁面上存在多条同轴穿透型裂缝，这些裂缝属于Ⅰ-Ⅱ型复合裂缝。假设无限大的岩体远端边缘上受到均匀分布的双轴压力分别为σy′和σx′的作用。以第1 条裂缝为研究的目标裂缝，分别建立直角坐标系x′oy′（x′轴和y′轴分别与远端σx′和σy′平行） 和直角坐标系xoy（x 轴与裂缝方向平行，y 轴与裂缝中垂线重合）。第1 条裂缝方向和σy′作用方向的夹角为β（称为裂缝角）。在裂缝面上（y=0，|x|＜a，a 为裂缝半长，单位为m）受到压力（σh+P） 的作用（σh为水平最小主应力，单位为MPa；P 为裂缝内净压力，即液体压力超出最小地应力的部分，单位为MPa）。假设第j 条裂缝与第1 条裂缝夹角为γj。

基于以上假设，受压脆性岩石Ⅰ-Ⅱ型复合裂缝水力压裂力学模型如图1（a）所示。应力符号采用弹性力学惯例。按照材料力学的规定，以拉应力为正，压应力为负；剪应力对单元体内任意点的矩为顺时针时为正。如图1 所示，无限大的岩体的边缘受均匀双轴压力作用，裂缝表面受水压力作用的裂缝问题扩展（问题a），可以转化成问题b 与问题c的叠加。

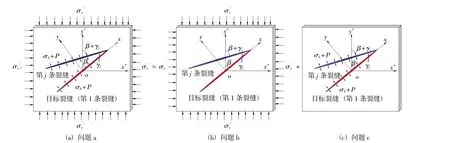
图1 受压脆性岩石Ⅰ-Ⅱ型复合裂缝水力压裂力学模型及叠加原理的应用

设在坐标系xoy 中，无限大的岩体远端边缘上应力分别为σx（对应x 轴） 和σy（对应y 轴） 及τxy，对于第j 条裂缝，分别为σx(j)、σy(j)、τxy(j)。对远端应力进行坐标系x′oy′和坐标系xoy 之间的坐标变换，得到坐标系xoy 中应力。

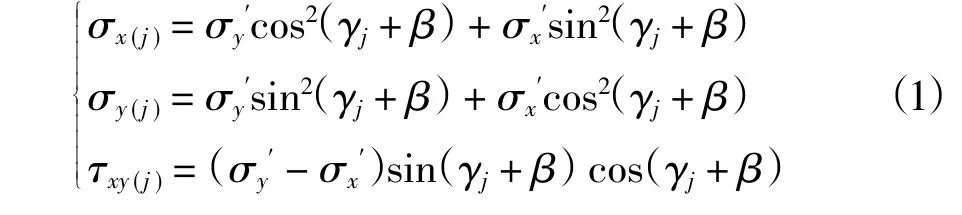
应力进行转标变换后，为更清楚地表达远端应力的变化，图1 可以表示为图2。

针对图2 的所示问题，根据岩体边缘应力大小，应用叠加原理可求得天然裂缝端部的应力强度因子如下。

图2 坐标变换后受压脆性岩石Ⅰ-Ⅱ型复合裂缝水力压裂力学模型及叠加原理的应用

式中，KΙa为问题（a）中裂缝端部的Ⅰ型应力强度因子，MPa·m1/2；KⅠb为问题（b）中裂缝端部的Ⅰ型应力强度因子，MPa·m1/2；KⅠc为问题（c）中裂缝端部的Ⅰ型应力强度因子，MPa·m1/2；KⅡa为问题（a）中裂缝端部的Ⅱ型应力强度因子，MPa·m1/2；KⅡb为问题（b）中裂缝端部的Ⅱ型应力强度因子，MPa·m1/2；KⅡc为问题（c）中裂缝端部的Ⅱ型应力强度因子，MPa·m1/2。

对于第j 条裂缝，问题（b）与问题（c）对应的裂缝缝端应力强度因子见式（3）。

情形一：主裂缝壁面上存在多条天然裂缝

对于主裂缝壁面（图3）上的天然裂缝，考虑实际受力状况，在直角坐标系x′oy′中，岩体边缘垂直方向受力σy′=-σv（σv为垂向地应力，MPa），水平方向受力σx′= -σH（σH为水平最大主应力，MPa）。在裂缝面上（y = 0，| x|＜a） 受到常压力（σh+P）的作用。

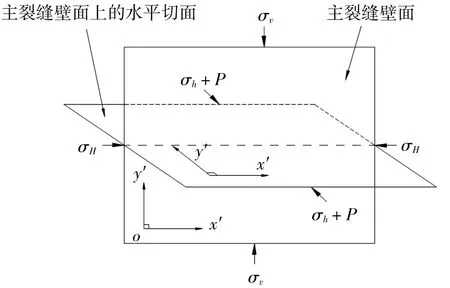
图3 主裂缝壁面受力示意图

结合裂缝壁面上岩石的实际受力状况，考虑应力符号，得到式（5）。

对于第1 条裂缝（目标裂缝），可看作是γ1=0（j =1）的特殊情形。

情形二：主裂缝壁面的水平切面上存在多条天然裂缝

考虑主裂缝壁面上的水平切面（如图3），当该面上存在多个穿透型裂缝时，远端边缘上受到均匀分布的周向压力分别为σy′和σx′的作用，此时σy′=-σh-P，σx′=-σH。在天然裂缝面上（y=0，|x|＜a）受到孔隙压力p0的作用（此时假设压裂流体压力尚没有传导到裂缝）。分析方法如上，得到式（7）。

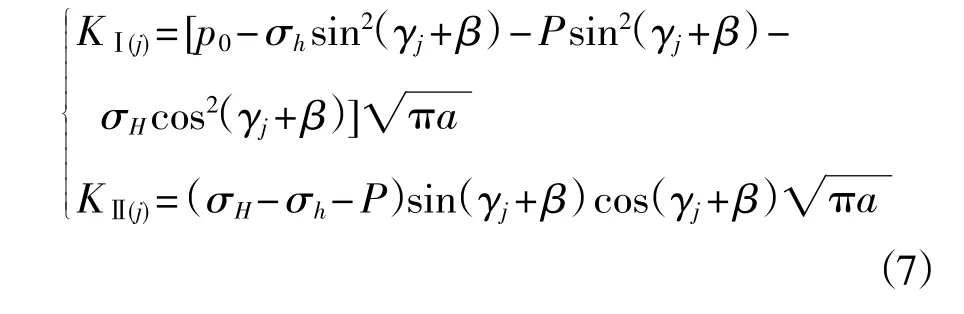
2 多裂缝应力干扰计算

假设所研究的无限大平面岩体中存在多条穿透型裂缝，远端存在正应力与剪切应力。以第一条裂缝为研究目标裂缝，位于水平方向。如前所述，在坐标系xx-o-yy 中，假设第j 条裂缝与第1 条裂缝同轴（端点相交于一点），缝间夹角为γj，如图4所示。

图4 多裂缝缝端应力叠加计算原理图

引入以裂缝端点为原点的极坐标（称为裂缝前缘坐标系），根据线弹性理论，在远端应力作用下，在目标裂缝（第1 条裂缝）裂缝尖端附近的极坐标系中，半径为r 的单位圆上圆周角度为θ 处（对应M 点）的应力极坐标表达式如下。

式中，σr(1)为极坐标系下第1 条裂缝尖端单元圆周上M 点的轴向应力，MPa；σθ(1)为极坐标系下第1 条裂缝尖端单元圆周上M 点的径向应力，MPa；τrθ(1)为极坐标系下第1 条裂缝尖端单元圆周上M 点的剪切应力，MPa；KⅠ(1)为第1 条裂缝尖端的Ⅰ型应力强度因子，MPa·m1/2；KⅡ(1)为第1 条裂缝的Ⅱ型应力强度因子，MPa·m1/2；r 为单元圆周距离裂缝尖端的距离，m。

对于任意第j 条裂缝，在极坐标中M 点的应力分量奇异项用下式表示（此时M 点在其极坐标中的圆周角度为（γj+θ））。

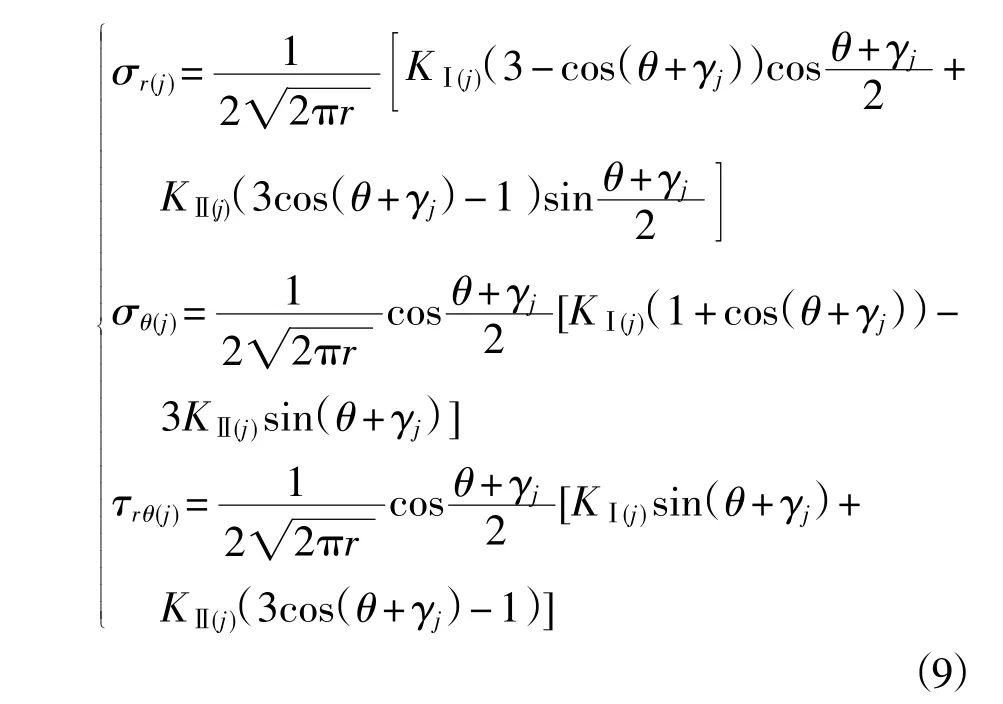
式中，σr(j)为极坐标系下任意第j 条裂缝尖端圆周上M 点的轴向应力，MPa；σθ(j)为极坐标系下任意第j 条裂缝尖端圆周上M 点的径向应力，MPa；τrθ(j)为极坐标系下任意第j 条裂缝尖端圆周上M 点的剪切应力，MPa；KⅠ(j)为第j 条裂缝尖端的Ⅰ型应力强度因子，MPa·m1/2；KⅡ(j)为第j 条裂缝的Ⅱ型应力强度因子，MPa·m1/2。

则对于Ⅰ-Ⅱ复合型裂缝问题，n 条同轴裂缝在M 点的应力组合见式（10）。

式中，σr为极坐标系下n 条同轴裂缝尖端M 点的轴向应力代数和，MPa；σθ为极坐标系下n 条同轴裂缝尖端M 点的径向应力代数和，MPa；τrθ为极坐标系下n 条同轴裂缝尖端M 点的剪切应力代数和，MPa。根据每条裂缝缝端应力大小，组合在一起时，得到M 点的应力。

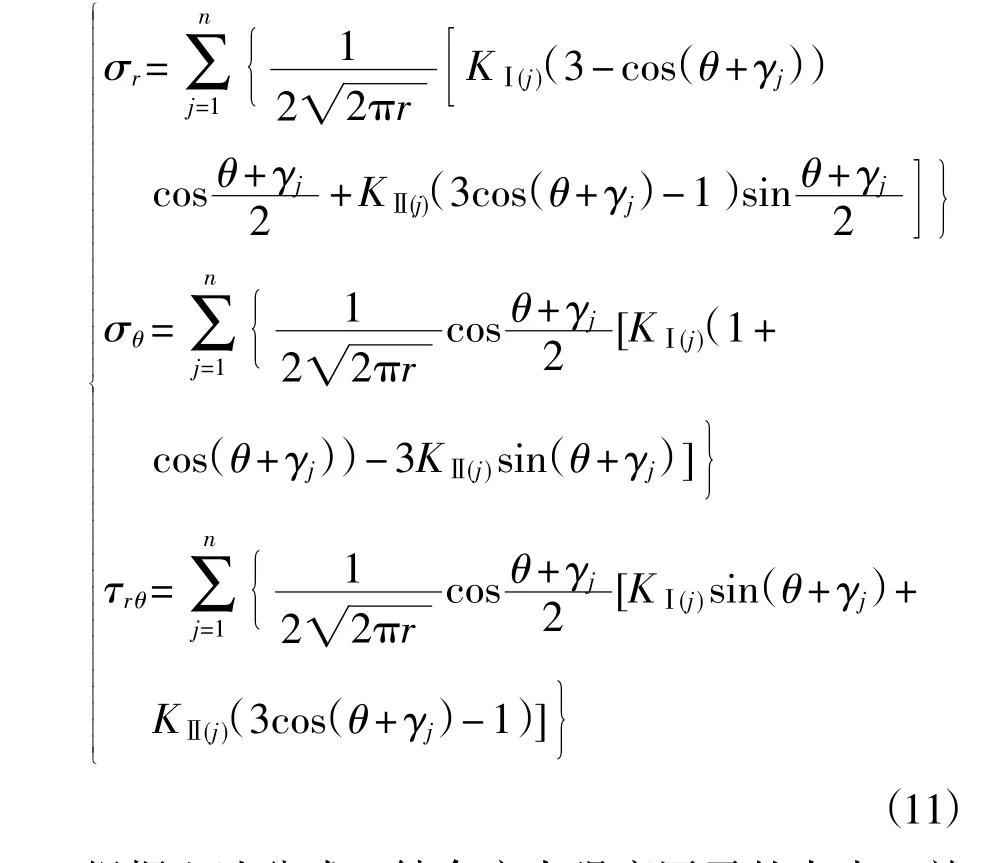
根据上述公式，结合应力强度因子的大小，就得到所研究裂缝尖端单位圆上任意角度处的应力大小。

3 多裂缝拉张破裂模型及应用

3.1 裂缝拉张破裂模型

3.1.1 最大周向拉应变理论

进行天然裂缝起裂分析的核心是选取合理的起裂准则。目前，还不存在一个万能的准则，能够适用于所有尺度和条件。本文拟用最大周向拉应变理论对上述模型进行起裂分析。最大周向拉应变理论认为：①裂缝起裂方向垂直于周向应变εθ最大的方向；②当εθmax达到临界值εc，裂缝开始起裂扩展。需要说明的是，边界载荷虽然为压剪载荷，根据起裂机理，在混合型断裂模式下，在岩体中天然裂缝的内部存在张应力（净压力、孔隙压力）的条件下，裂缝端部可能产生拉张破裂或剪切破裂，两种破裂在达到一定条件后都可能产生。本文重点讨论的是最大拉应变破裂，剪切破裂在另外场合讨论研究。

3.1.2 裂缝起裂扩展的方向

平面应变情形下，所研究对象3 个方向均有受力，只在平面内有应变，与该面垂直方向的应变可忽略。平面应力条件变为平面应变时，弹性模量与泊松比都要发生变化，分别用下式代替。

式中，KⅠ(j)、KⅡ(j)分别为I、Ⅱ型裂缝端部的应力强度因子。根据最大周向拉应变理论，裂缝起裂扩展的方向应满足以下条件。

式（16）为按最大周向拉应变理论所预测的多裂缝干扰情况下的开裂角公式，开裂角度由泊松比、裂缝尖端的应力强度因子KⅠ(j)和KⅡ(j)确定。

3.1.3 裂缝起裂扩展的条件

最大周向拉应变理论认为，当εθmax达到临界值εc时，裂缝开始起裂扩展。当只存在第1 条天然裂缝（目标裂缝）时，当εθmax=εc，且KⅠ(1)=KⅠc，KⅡ(1)=0（纯I 型裂缝），KⅠc为材料的断裂韧性。此时θ0=0。根据（14）式，可得式（17）。

公式（18）就是按照最大周向拉应变理论建立的Ⅰ-Ⅱ型复合型的断裂准则。

3.2 裂缝拉张破裂模型应用分析

3.2.1 主裂缝壁面存在1 条裂缝拉张破裂

基础参数：根据川东南地区川焦石坝构造高部位页岩气水平井焦页M 井压裂设计书，目的层段为志留系龙马溪组2 769～3 607 m，全井段水平段岩性，主要为黑灰色碳质泥岩和深灰色粉砂质泥岩。σh=50.39 MPa，σH=63.50 MPa，σv=58.2 MPa，μ=0.2，p0= 30 MPa，E = 2.6 × 104MPa，KⅠc= 1 MPa·m1/2，裂缝长度a=0.05 m。第1 条裂缝，β=60°，γ1=0。

考察主裂缝壁面上天然裂缝（层理、弱面）进行扩展并形成体积缝网的条件。根据式（16），代入应力强度因子式（6）后，得到θ0满足的公式；再根据式（18），代入应力强度因子式（6），得到应变满足的公式。联立以上公式，得到满足第1 条裂缝的尖端发生张性破裂（最大张应变）的最小净压力P。

固定σh=50.39 MPa，σH=63.50 MPa，逐步改变垂向压力σv的大小，计算不同垂向压力下，第1条裂缝（目标裂缝）端部发生张性破裂的最小净压力，得到表1。令δ = （σH- σv）/σv为垂向应力系数。根据模拟结果，随着垂向应力差异系数减小（垂向应力增加），裂缝最小起裂净压力增加，夹角逐渐减小。可见，裂缝的扩展与垂向应力的大小有重要关系。垂向应力越小，则越容易形成缝网。根据本井地应力条件，对于a=0.05 m 的天然裂缝，1条裂缝时，裂缝扩展净压力为6 MPa；2 条裂缝时，裂缝扩展净压力为5.6 MPa；3 条裂缝时，裂缝扩展净压力为5.3 MPa。当天然裂缝条数增加，会降低开启净压力，有利于形成主裂缝壁面上的裂缝网络，达到体积压裂的效果。本井实际施工时，净压力为5～12 MPa，所预测的天然裂缝净压力在此范围内，压裂过程中形成了理想的压裂缝网，天然气无阻流量43.8×104m3/d。

表1 垂向地应力变化时，裂缝开启净压力的变化

如表2 所示，只存在第1 条裂缝时，在给定的三维地应力条件下，随着天然裂缝与垂向夹角角度的增加，裂缝呈现拉张破裂所需要的缝内压力逐渐增加。相比有一定角度倾斜的裂缝，垂向天然裂缝容易破裂扩展（且不需要较大的净压力，小于最小主应力的滤液压力即可破裂），而向水平方向倾斜的层理裂缝难以破裂，且角度越大，越难以破裂。可见，垂向发育的天然裂缝有利于形成缝网。

表2 裂缝角度变化时，裂缝开启净压力的变化

3.2.2 主裂缝壁面上存在2 条、3 条裂缝拉张破裂的条件

沿用3.2.1 部分的地层参数。此时取j =1、2、3，γ1=0，γ2=20°，γ3=40°，根据式（16），得到存在2 条、3 条裂缝时，第1 条裂缝端部的张性开启角度θ0满足的公式。再联立式（18），得到结果见表1、图5。根据模拟结果，在同样地应力条件下，存在2 条、3 条裂缝时，使得天然裂缝破裂的净压力降低，有利于形成裂缝网络。可见，存在同轴（相交）的天然裂缝，或者延伸后形成相交的裂缝时，继续破裂的净压力大幅度降低，形成裂缝网络的可能性增加。

图5 垂向地应力变化时，开启净压力的变化

3.2.3 水平切面存在1 条裂缝时拉张破裂

存在1 条裂缝时γ1=0，根据式（16），代入应力强度因子式（6）后，得到θ0满足的公式；再根据式（18），代入应力强度因子式（6），得到应变满足的公式。联立以上公式，得到满足第1 条裂缝的尖端发生张性破裂（最大张应变） 的最小裂缝内压力p0。根据模拟结果（表3、图6），在给定的地应力条件下，随着天然裂缝与最小主应力方向夹角角度的增加，裂缝呈现拉张破裂所需要的缝内压力逐渐减小。与最小主应力方向的夹角越小，破裂压力越大；与最小主应力方向的夹角越大（与最大主应力方向的夹角越小），破裂压力越小，且不需要较大的缝内压力，具有一定大小的滤液压力（小于最小主应力）即可破裂。可见，与最大主应力方向一致的天然裂缝，有助于形成裂缝网络。

表3 裂缝角度变化时，开启压力的变化

图6 裂缝角变化时，裂缝开启压力的变化

3.2.4 水平切面存在2 条、3 条裂缝时拉张破裂

沿用3.2.1 的地层参数。取j=1、2、3，γ1=0，γ2=20°，γ3=40°。根据式（16），代入应力强度因子式（6）后，得到存在2 条、3 条裂缝时，第1 条裂缝端部的张性开启角度θ0满足的公式。再联立式（18），得到结果见表3、图6。存在2 条裂缝、3 条裂缝时，在同样地应力条件下，使得目标裂缝张性破裂的缝内压力均降低，甚至略大于孔隙压力即可开启。

4 结 论

我国海洋油气资源丰富，加强对非常规油气资源开发技术的研究是海洋油气高效开发的途径，而体积压裂技术是提高海洋页岩油生产产量的关键技术，研究清楚水力压裂过程中，岩体内存在多个天然裂缝的情况下，裂缝壁面上天然裂缝的扩展规律，对于体积压裂技术的顺利实施、水力压裂参数的设计、裂缝形态的认识至关重要。

本文采用应力叠加原理，建立了压剪条件下，受到相邻裂缝影响时，目标裂缝张性起裂扩展的准则。结合水力压裂过程，主要研究了水力压裂主裂缝壁面上及主裂缝两侧脆性岩体水平切面上天然裂缝的起裂方向及起裂条件模型。

根据模拟可知，在水力压裂主裂缝壁面上，随着垂向应力减小，使得天然裂缝开启的最小净压力减小，天然裂缝开启更容易。因此天然裂缝的扩展与垂向应力的大小有重要关系，垂向压力越小则越利于形成缝网。当天然裂缝条数增加时，天然裂缝开启所需要的净压力降低，这样有利于形成裂缝网络，达到充分改造的效果。相比倾斜赋存的天然裂缝，垂向发育的天然裂缝容易破裂扩展，而朝向水平方向倾斜的层理性裂缝难以破裂。可见，垂向发育的天然裂缝有利于形成缝网，对形成裂缝网络更有价值。在主裂缝两侧岩体的水平切面上，天然裂缝与最小主应力方向的夹角越大，破裂压力越小；且缝内压力小于地层最小主应力时，即可破裂。存在多条裂缝时，目标裂缝张性破裂的缝内压力均降低。上述模型及应用模拟揭示了脆性岩石在水力压裂过程中，主裂缝壁面岩体中形成复杂裂缝网络的内在机理。