一种基于最短路径分析的双向交互模式排队系统构建

容尔健，易桂轩，魏金占，蔡素影

(1.广东中冶地理信息股份有限公司，广东 东莞 523000； 2.武汉市测绘研究院，湖北 武汉 430022；3.北部湾大学，广西 钦州 535000)

1 引 言

排队等号系统在社会领域扮演非常重要的角色，对于社会稳定，人民素质的提升意义重大。但传统的广播模式排队等号系统不能及时与客户沟通，很容易造成客户时间的浪费，同时因为各类原因造成排号机会错失需要再次排号，给客户造成巨大浪费，极易造成服务方和客户的矛盾，增加社会不稳定因素。

近年来随着物联网技术快速发展，排队等候业务逐渐与个人多媒体终端如手机、平板等融合，客户可以在多媒体终端实现电子排号申请。这些手段在一定程度上方便了客户，节约了一定时间，但本质上与纸质申请或排队等候模式差异不大，都是以时间序列为基准的单向模式，仍有巨大的提升空间。

对于排队问题的本质，实际上是服务资源的单一串行服务于突发的并行服务需求的矛盾。基于此理解，对于串行单向服务，一是增加服务资源，二是将服务对象合理分组串行化，即通过排队候服以实现两者的匹配，达到服务数量与服务对象的合理匹配。

从空间信息学的角度分析，可以做如下分析：一是服务点的位置不变；二是服务对象的空间分散与动态化；三是服务对象运动轨迹沿着道路行进。基于此三个基本特点，可以通过基于服务点的范围分析，对服务对象进行分组，协助两者实现合理匹配。

结合以上分析，可以认为该问题将涉及范围分析、最短路径分析和时空互动，基于此笔者提出一种交互式的排队等号方法，其主要依托空间位置关系，充分考虑客户的时间安排，做到等号效率与客户时间利用率的最佳组合。

2 问题解决

服务点不动服务对象从多方位靠近，因此就涉及两个核心技术：点点之间的最短路径问题和服务范围问题。

对于点点之间的最短路径问题，这是一个经典空间问题。对于最短路径技术，当前常见技术多以数学方法和生物学思维实现问题求解。前者以Dijkstra算法为主，后者以蚁群算法、遗传算法为主[1～6]。

对于前者，该算法具有可以求得精确解的特性，而且对于样本空间的所有结点都可以求得最短路径，因此在面向点对点服务时，当数据量较大则该算法适用性和效率欠佳[5]。

对于生物学思维，其采用进化思维，该类方法的特点是可以并行计算，但难于给出最优解，因此适用于并发、高效率路径最短搜索[6]。

本问题最短路径具有服务点不动特性，路网不会轻易变更的特性，基于此对于前者，可以采用传统Dijkstra算法，将每个样本空间的节点间的最短路径求解，过滤出基于服务点的所有最短路径[5]。待客户发出需求服务时，临近节点迅速被选中并调出该结点到最近服务点的最短路径。其特点是也决定了对样本量的要求不能过大，可以前期进行预运算，适用于一般规模城市的该类问题解决。

若采用生物学类的相关技术，因其具有并发高效的特点，适用于大范围、高效率的路径分析，因此不需要进行预运算即可实现问题求解[6]。该类技术原理简单易于实现，特别适合于云时代并行计算，因此对于建设各类城市大脑模式服务的资源调度具有普适性。

以上技术虽然具有最优和最快的特点，各有优劣，但是经过分析可知，前者最怕的是样本空间的扩大化，后者最怕的是快的同时缺失精准度。因此可以将后者的搜索结果，作为前者的样本空间，进而实现两种技术优劣互补。

笔者选用由魏金占等人提出的基于空间分析技术的最短路径搜索技术。其特点在于通过将样本区间通过升维进行拓展，将长度区间升维到椭圆空间，通过面空间约束搜索范围，进而实现了最短路径搜索。与前两者相比，其特点是可以实现实时、动态、海量样本的最优搜索，是将以上两种思维进行融合的新产物[7～11]。特别是其利用的是空间分析相关技术，与本问题求解的覆盖分析部分，技术同源，因此对于该问题的求解，本文优选采用空间思维的新技术。

对于覆盖问题，通常可以采用简单缓冲区分析思维来实现。但由于行人多基于道路行动，因此简单缓冲区思维将造成实际点位到服务点的道路距离大于直线距离。基于此弊端，结合如上提及的距离升维方法，将对样本区间进行如下操作：

首先确定客户行进的速度和距离，得到其返回的最理想时间。把距离减半，以服务点为中心，将所有减半后的范围内路口节点都作为满足条件的节点。对于处于一半距离以上但在该距离之内的，通过空间分析过滤后，将各个节点到服务点的最短距离求解出来，满足条件标识出来。最后将所有处于该环内的满足条件的节点依次相连，范围内部即为该客户的自由活动范围。

该步骤的优势在于通过一半距离的过滤，减少计算机的运算量。后期通过距离分析，过滤出最终范围，类似于双层过滤，结合自然思维“设置的约束条件越多”求解速度越快，实现了问题求解快与准的协调统一[12]。

3 案例分析

基于以上思维，本文旨在提供一种双向互动模式的排号呼叫方法，该方法克服现有排号系统单向广播模式的缺陷，实现了客户与服务点的双向互动，具有原理简单，易于实现、适用性强的特点[12]。

为了简化问题，对于活动区域的定义，暂时只采用缓冲区分析模式，通过距离判定实现问题分析，实际实现时必须结合路网实际进行细化，确保问题求解的精确可靠[12]。

图1为本文实施例的服务点与客户位置点示意图，图中各部分名称及序号如下：

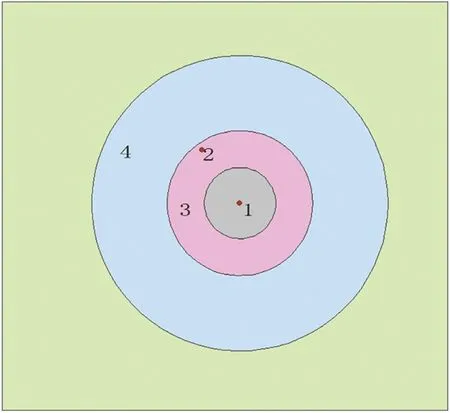
图1 服务点、客户位置及范围类别示意图

1为服务点，2为客户位置点，3为当次叫号时间差对应范围，4为下班前时差对应活动范围。

下面结合图2和实施例具体说明本发明的实施过程：

图2 客户及时返回范围示意和保留资格范围示意

A、计算当前号码与客户号码的差值n=10；

B、根据差值及平均服务时间t=5 min，预估排队时间T=n×t=10×5=50；

C、以预估排队时间为准，根据交通方式的参考速度v=5 km/h，分析出活动范围R=n×t×v=10×5×5÷60=4.16 km，取整为4 km；

D、以如图2中第一个4 km范围小圆为界，若在该范围内呼叫客户并给出返回时间建议，若超出范围，下一位客户进入步骤A，当前客户进入步骤E；

E、以下班时间为准得到当前时间差Tt，当前时间为9点，下班时间12点，时间差3个小时，计算出对应活动范围区Rt=Tt×v=3×5=15 km；

F、以如图2中第二个15 km范围大圆为界。若该范围内通知客户是否愿意返回，若同意则保号保留排队资格，若不同意则进入步骤G；

G、取消排队资格，下一位客户进入步骤A。

2、步骤D中包括以下步骤：

D1、以步骤C所生成的如图2中第一个4 km范围小圆为例，分析客户当前位置是否在缓冲区内；

D2、若在缓冲区内如图2中1号客户位置，则根据当前客户位置及参考速度计算到达服务点的时间并通知客户在该时间内返回服务点；

D3、若在缓冲区外，则通知当前客户超出排队距离，下一客户自动进入步骤A，当前客户进入步骤E；

所述的步骤D2优选基于空间分析技术的最短路径搜索算法[8]，若求得最短路径长度为S=3 km，则返回路程时间为36 min，排队时间为50 min，则客户必须在14 min内返回；

4、步骤E中包括以下步骤：

以下班时间12点，当前时间9点为例，时间差Tt=3 h，交通方式的参考速度v=5 km/h，测算出下班前返回范围半径Rt=Tt×v=3×5=15 km，以服务点生成如图2中第二个15 km范围大圆为界的缓冲区。

5、步骤F中包括以下步骤：

F1、以步骤E所生成的15 km范围缓冲区为例，分析客户当前位置是否在缓冲区内；

F2、若在15 km范围缓冲区内如图2中2号客户位置，则根据当前客户位置及参考速度计算到达服务点的时间并通知客户在该时间内返回服务点，若当前客户不同意则进入步骤G；

F3、若在15 km范围缓冲区外，则通知当前客户超出排队距离，当前客户进入步骤G；

所述的步骤F2优选基于空间分析技术的最短路径搜索算法[8]，若求得最短路径长度为10公里，则返回路程时间为10÷5×60=120 min，预留排号时间为180 min，则客户必须在180-120=60 min内返回[12]。

4 小 结

本排号方法通过客户和服务点位置，计算出服务时间差，为客户进行其他社会活动提供参考。其特点在于将时空因素和人机交互综合运用，变更了传统排号系统广播模式，同时对于首次排号机会错失的客户，在不影响他人服务质量同时，人性化考虑个性需求[12]。此外该发明也间接地存在加急排号而不影响他人服务质量的可能，对提升客户体验、节约社会资源、减少社会不稳定因素都具有重要意义。本发明技术原理简单成熟，是将串行服务与并行服务矛盾解决的新思路，可以在社会各个行业进行推广，应用潜力巨大。