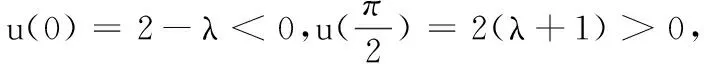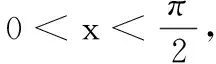对一道全国高中数学联赛试题的探究*

湖南省长沙市周南中学 (410201) 周思宇 谢建军 刘四平

一、试题呈现

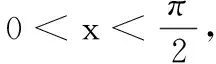
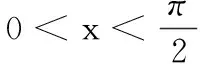
二、背景探究

三、试题推广

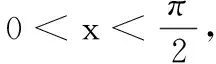
解析：当λ≤0时，由①式知tanx-x>0，x-sinx>0.所以tanx-x>λ(x-sinx)恒成立，故tanx+λsinx>(λ+1)x恒成立.

现考虑λ>0时的情况.

(ⅰ)当λ=2时，tanx+2sinx>3x恒成立.

(ⅱ)当0<λ<2时，u(x)>u(0)>0，故g′(x)>0，即g(x)单调递增，所以g(x)>g(0)=0，即f′(x)>0，所以f(x)单调递增，即f(x)>f(0)=0，所以tanx+λ(sinx-x)-x>0，故tanx+λsinx>(λ+1)x恒成立.