短肢剪力墙新型多垂直杆单元模型研究

张品乐, 王金玉琳, 张智吉, 贾 毅, 陶 忠

(昆明理工大学建筑工程学院， 昆明 650500)

由于建筑功能的需要，在实际工程中大部分短肢剪力墙是由一字形截面短肢剪力墙组合而形成的T形、C形、U形和L形等形式[1]. 现有研究多集中于剪力墙抗震性能研究[2-4]，对钢筋混凝土(reinforced concrete，RC)异形截面短肢剪力墙，尤其是高强箍筋约束钢筋混凝土L形截面短肢剪力墙抗震性能方面的研究较少. 因此，本文以钢筋混凝土L形截面短肢剪力墙为研究对象，对其进行低周往复加载试验研究. 通过变化剪跨比、轴压比及无翼缘腹板端部箍筋间距等设计参数来探究此类构件的抗震性能.

由于翼缘和腹板的相互作用，钢筋混凝土异形截面短肢剪力墙的受力机理与变形状态非常复杂[5-6]. 建立能够真实反映其力学性能和变形状态的力学模型，为我国广大地震区建造这类新型结构提供科学计算依据，具有重要的理论意义. 常见的短肢剪力墙力学模型主要有：空间薄壁杆件模型、等效梁模型[7]、壳元模型[8-9]、梁壳模型[10]及多垂直杆模型等[11-14]. 上述力学模型不便处理各种异形截面，较少能够考虑墙体弯剪相互作用；且多数模型基于平截面假定建立，不能考虑剪力滞后效应影响；此外，现有力学模型较少能够考虑材料动态损伤累积效应影响，更不能直接评估结构的地震损伤程度，只能预先通过结构地震反应分析，最后基于反应量，借用某种损伤评估模型来间接预测结构震后损伤状态[15]，其评估的准确性无法衡量. 鉴于此，本文以多垂直杆元模型为基础，通过结合多垂直杆的轴向刚度和剪切刚度来考虑多垂直杆中正应力对剪切刚度的影响，引入剪力滞后翘曲位移函数和材料动态损伤累积指标，建立能够考虑剪力滞后和材料连续损伤累积效应影响的钢筋混凝土短肢剪力墙非线性分析单元模型，以此来精确模拟钢筋混凝土异形截面短肢剪力墙的真实力学响应. 最后对低周反复荷载作用下的高强箍筋约束钢筋混凝土L形截面短肢剪力墙进行非线性数值模拟，对比试验结果验证新型多垂直杆单元模型的有效性.

1 短肢剪力墙非线性分析单元模型

1.1 剪力滞后翘曲位移函数

图1为试件的有限元模型图，本研究将短肢剪力墙模型沿高度划分3段进行数值模拟，将短肢剪力墙截面共划分为21个多垂直杆，分析多垂直杆中正应力对剪切刚度的影响，每根垂直杆均考虑了轴向刚度和剪切刚度，即每根垂直杆传递轴力的同时还传递剪力.

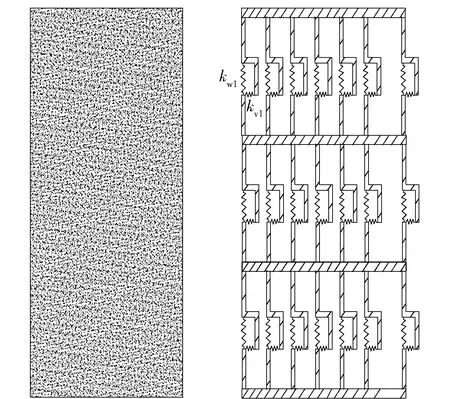
kw1为第1根垂直杆的轴向刚度；kv1为第1根垂直杆的剪切刚度. 图1 试件的有限元模型Fig.1 Finite element model of specimen

图2为多垂直杆单元模型，在多垂直杆单元模型中引入剪力滞后翘曲位移函数来考虑剪力滞后效应. 对腹板远离翼缘中和轴的L形截面短肢剪力墙，其截面位移模式可表示为

w(x,y,z)=wo-xθy+yθx+wζxζx+wζyζyv(x,y,z)=vsu(x,y,z)=us

(1)

式中：w(x,y,z)为截面w任意点处的线位移分量；v(x,y,z)为截面v任意点处的线位移分量；u(x,y,z)为截面u任意点处的线位移分量；θx为L形截面绕x轴任意点的角位移；θy为L形截面绕y轴的角位移；wo为形心o位置的初始竖向位移；vs为剪切中心s位置在y方向的线位移；us为剪切中心s位置在x方向的线位移；ωζx为xoz平面内因为单位剪滞变形ζx=1而产生的剪力滞后翘曲位移函数；ωζy为yoz平面内ζy=1而产生的剪力滞后翘曲位移函数.

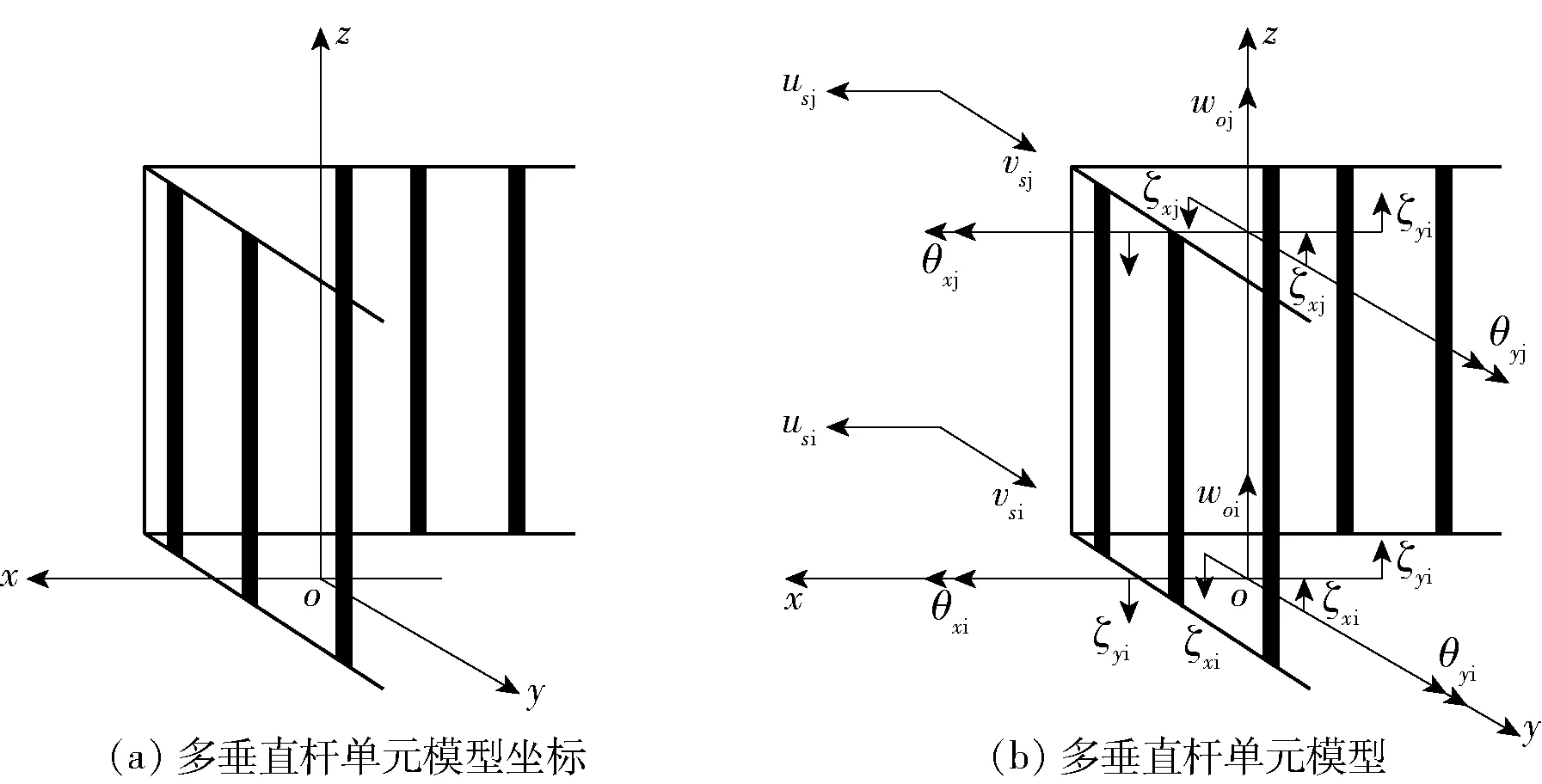
图2 考虑剪力滞后效应的多垂直杆单元模型Fig.2 Multi-vertical truss shear wall member mode

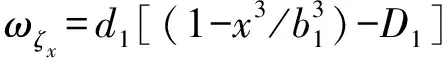
(2)

(3)

式中：d1和d2分别为翼缘中面至形心轴的距离和腹板中面至形心轴的距离；D1=3tb1/(4A)；D2=3tb2/(4A)；b1和b2分别为翼缘与腹板的宽度；t为墙体厚度；A为墙体截面面积.

1.2 考虑剪切滞后和材料动态损伤累积效应的单元刚度矩阵

单元两端的自由度和相应的杆端力向量分别表示为

(4)

(5)

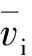
(6)

(7)

式中：r=0.5[16]，代表墙体转动高度与墙高之比根据小变形假定，sinθxi=θxi，sinθxj=θxj[17]，式(7)减去式(6)，得到因为剪切变形而引起的相对位移为

(8)

同理，能够得到第m根杆的轴向变形为

δωm=ωoj-ωoi+am(θxj-θxi)+ym(ζxj-ζxi)

(9)

式中：am为第m根杆距离横截面轴的水平距离；ym为第m根杆的剪切翘曲函数值.

混凝土单轴拉压循环时的累积损伤指标[18]为

(10)

(11)

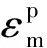
(12)

式中：Asi为钢筋面积；Aci为杆单元中混凝土面积；γ为损伤指标校核系数，取γ=6[18].

第m根垂直杆在第j次加载循环周期后的轴向刚度为

kωmj=(1-ξ1Dc,mj)kcm+(1-ξ2Ds,mj)ksm

(13)

式中：Dc,mj表示为第m根垂直杆中混凝土材料在经历第j次循环加载后的损伤值；Ds,mj表示为第m根垂直杆中钢筋在经历第j次循环加载后的损伤值；kcm为该垂直杆所模拟的截面积混凝土材料的初始轴向刚度；ksm为该垂直杆所模拟的截面积钢筋的初始轴向刚度；ξ1和ξ2分别为混凝土和钢筋的损伤常数，取ξ1=0.27，ξ2=0.23[20].

轴向变形引起的墙单元应变能计算公式为

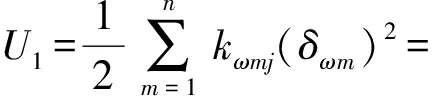
(14)

剪切变形引起的墙单元应变能计算公式为

(15)

式中kvmj为第m根垂直杆经历第j次循环加载后的剪切刚度，其值可以根据多垂直杆的不同状态来确定[21].

墙单元端部节点力F在节点位移d上做的功为

W=-dTF

(16)

总势能为

Π=U1+U2+W

(17)

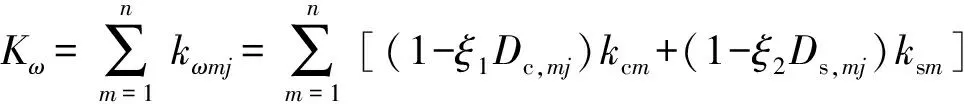
根据变分原理，推导出yoz平面内的单元刚度矩阵K为

(18)

同理，xoz平面内的单元刚度矩阵可以按照式(18)得到，平面yoz和xoz在局部坐标下的单元刚度矩阵得到后，按式(4)(5)所排列的自由度顺序可得到空间单元刚度矩阵[22].

2 高强箍筋约束钢筋混凝土异形截面短肢剪力墙拟静力试验与非线性分析

2.1 试验概况

设计了6个L形截面高强箍筋约束钢筋混凝土短肢剪力墙试件，采用C40混凝土浇筑，试件的高度和宽度分别为1 400、100 mm，设计参数见表1. 各试件的截面配筋如图3所示，分别布置了8、12 mm的受力纵筋，采用4 mm的高强钢筋配箍，详细的钢筋实测力学参数见表2. 现场试验测试得到的立方体抗压强度平均值为47.2 MPa.

试验测试装置如图4所示，试验加载方案采用力- 位移混合加载制度，首先采用油压千斤顶在试件截面形心处施加竖向力并加载至设计轴压力并保持稳定. 水平加载制度分2步进行，见图5，试件屈服前采用荷载控制，试件屈服后采用位移控制加载制度，按照屈服位移Dy的倍数进行逐级循环加载，每级循环3次. 当构件承载力下降至峰值承载力的85%或试件破坏时停止加载.

表1 试件设计参数

图3 试件配筋(单位：mm)Fig.3 Reinforcements details (unit: mm)

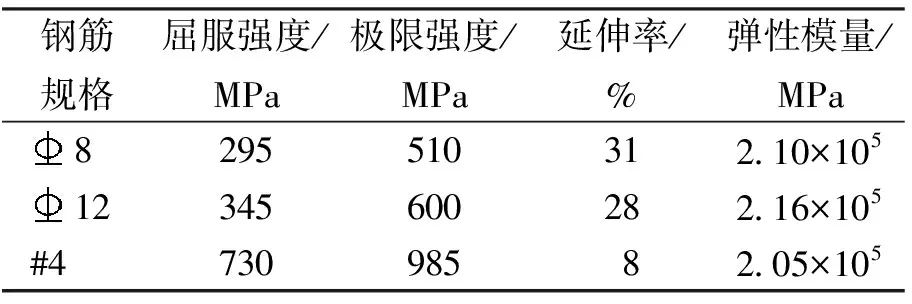
表2 钢筋实测力学性能

图4 测试装置整体Fig.4 Test setup

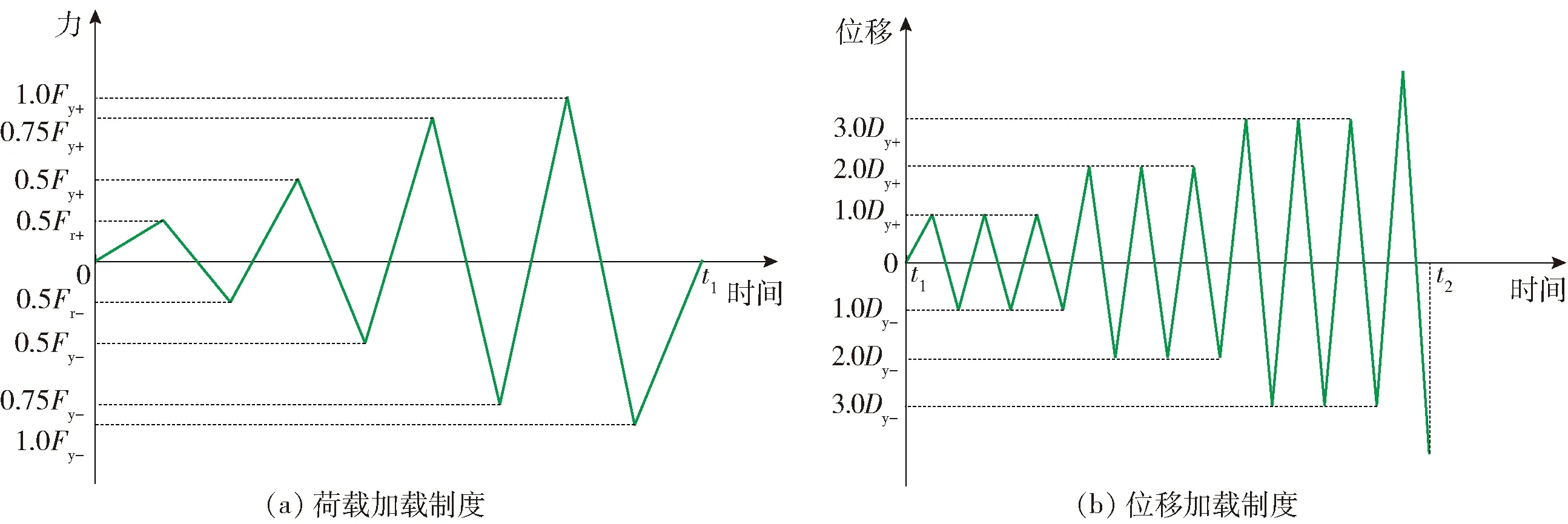
Fr、Fy、Dy分别代表开裂荷载、屈服荷载、屈服位移，符号“+”表示正向加载，符号“-”表示负向加载，以腹板受拉为正向加载，腹板受压为负向加载. 图5 加载制度Fig.5 Loading program

2.2 试件破坏特征及损伤历程分析

试验观察到6个试件的破坏特征均表现为受拉纵筋屈服及无翼墙腹板端约束边缘构件底部混凝土被压碎的弯曲破坏. 现以HSL650-1试件为例，说明试件的破坏特征及损伤历程，试件HSL650-1的破坏形态如图6所示，所有试件的损伤历程如图7所示. 如图6所示，正向加载至100 kN时无翼缘腹板端底部出现轻微水平裂缝，此时Dy=0.10，此阶段前可认为试件基本完好. 正向继续加载至140 kN时腹板水平裂缝加宽至0.2 mm，此时Dy=0.20，此阶段可认为试件发生轻微破坏. 反向加载至180 kN时试件反向加载屈服，此时Dy=0.60，此阶段可认为试件出现中度损伤. 此后采用位移控制加载方式. 3倍正向加载屈服位移下最外层纵筋出现拉断情况，此时Dy=0.90，此阶段可认为试件出现严重损伤，见图6(a)；3倍反向加载屈服位移下无翼墙腹板端底部边缘混凝土出现压溃剥落现象，承载力急剧下降，试验结束，此时Dy=0.96，见图6(b). 整个试验加载过程中翼缘及翼缘和腹板交接位置处混凝土无压碎现象出现，见图6(c).

图6 试件HSL650-1裂缝分布及破坏形态Fig.6 Crack patterns and failure modes of HSL650-1

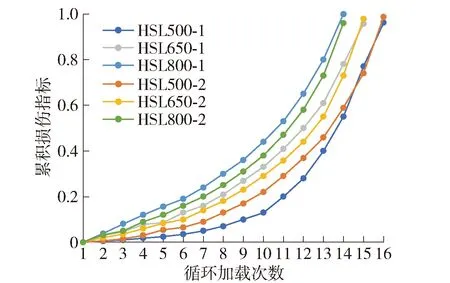
图7 短肢剪力墙损伤历程Fig.7 Damage evolution of short-limb shear wall

2.3 滞回性能分析

试验测试得到的荷载(F)- 位移(Δ)曲线如图8所示，各荷载- 位移曲线的滞回环比较饱满，呈现较好的耗能能力. 在正向加载和反向加载下的滞回环呈现不对称现象. 腹板受压时承载力大但延性差，腹板受拉时承载力小而延性好. 如果在腹板端部同时使用高强纵筋和高强箍筋则可使得L形截面短肢剪力墙在受拉、受压2个方向的受力性能更为均匀[23].

2.4 承载力及变形能力分析

各试件在不同特征状态下的承载力和变形能力见表3所示，由表3可知：随着剪跨比的减小，试件延性明显下降. 例如保持轴压比0.2不变，从剪跨

图8 试验荷载- 位移滞回曲线Fig.8 Lateral load-top displacement hysteretic loops of test

表3 承载力与变形能力

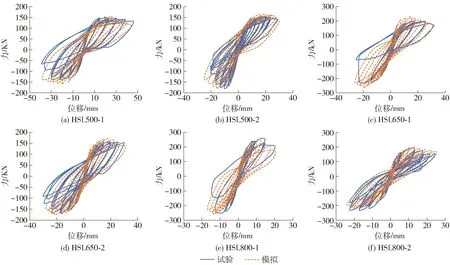
图9 试件计算滞回曲线及试验滞回曲线对比Fig.9 Hysteretic curves of calculation and test

比为2.80减小到2.15时，试件HSL650-1延性较HSL500-1下降34.6%；从剪跨比为2.15减小到1.75时，试件HSL800-1延性较HSL650-1下降44.1%. 随着轴压比的提高，试件承载力增加，但延性明显下降. 由于密配较细直径的高强箍筋能够有效约束无翼缘腹板端部混凝土受压产生的横向变形及抑制纵筋屈曲，所有试件的塑性变形能力较好，破坏时的位移角都大幅度超过规范中的弹塑性层间位移角限值(1/120).

2.5 计算与试验结果对比

为验证本文提出的计算模型，笔者对所有试件在拟静力作用下的滞回性能进行非线性数值模拟分析，得到其基底剪力与顶点位移之间的模拟滞回曲线，模拟滞回曲线和试验滞回曲线的对比见图9所示. 由图9可知，模拟滞回曲线和试验滞回曲线在承载力和变形能力等方面都较为接近，整体吻合度也较好，验证了本文所提出的钢筋混凝土短肢剪力墙新型多垂直杆单元模型比较合理，模型可以精确模拟钢筋混凝土异形截面短肢剪力墙的真实力学性能和变形状态，可用于钢筋混凝土异形截面短肢剪力墙的非线性分析.

3 结论

本文进行了钢筋混凝土异形截面短肢剪力墙的低周反复加载试验与精细化非线性分析单元模型研究，主要结论如下：

1) 本文引入剪力滞后翘曲位移函数和材料动态损伤累积指标，在多垂直杆单元模型的基础上建立能够考虑剪力滞后和材料动态损伤累积效应影响的钢筋混凝土异形截面短肢剪力墙非线性分析单元模型，改进的多垂直杆元模型能够精确模拟异形截面短肢剪力墙的真实力学性能和变形状态，可用于异形截面短肢剪力墙的非线性分析.

2) 无翼缘腹板端部密配较细直径的高强箍筋能够有效约束无翼缘腹板端部混凝土受压产生的横向变形及抑制纵筋屈曲，高强箍筋约束异形截面短肢剪力墙具有非常好的耗能能力和延性.

3) 钢筋混凝土异形截面短肢剪力墙试件均发生弯曲破坏，破坏集中在无翼缘腹板自由端的边缘构件内，应加强无翼缘腹板端部约束边缘构件设计，防止无翼缘腹板端部提前发生受压破坏.