基于深度全连接神经网络的离港航班延误预测模型
2022-11-08徐海文史家财汪腾
徐海文,史家财,汪腾
(1.中国民用航空飞行学院 理学院,四川 广汉 618307;2.中国民用航空飞行学院 民航安全工程学院,四川 广汉 618307)
0 引言
随着航班运输量的大幅提升,空中交通运输网络趋向饱和,恶劣天气、超负荷流量等原因导致的航班延误越来越多;同时航班延误会造成时间、人力和物力等方面的大量损失。譬如,朱江等[1]测算国内2018 年4 家主要航空公司的延误成本达720.93亿,美国2016—2019 年直接延误成本超过200亿美元[2];再者航班延误旅客的滞留会引起人群密度的变化、情绪稳定性降低,旅客行为亦会逐渐发展为扰乱行为,从而加深旅客与机场、航空公司的矛盾[3]。因此,针对航班延误相关问题做出预先分析与更准确的预测,可以让机场、航空公司及相关单位提前做好准备工作,进而提升航班运行服务质量,减少航班延误带来的经济损失,对民航系统的安全有序运行有着重要意义。
国内外众多研究学者对航班延误预测问题进行了深入研究,谌婧娇[4]基于Spark 平台的决策树算法对航班延误问题进行预测;高旗等[5]针对民航终端区拥堵问题,结合粒子群优化算法建立基于反向传播(Back Propagation,BP)神经网络拥堵等级预测模型;唐红等[6]改进负对数似然损失函数,基于非线性赋权极限梯度提升(eXtreme Gradient Boosting,XGBoost)算法对航班延误进行分类预测;宋捷等[7]利用机场航段历史航班运行数据,构建航班起降延误预测模型人工神经网络模型。
上述研究通过改进算法,取得了较为准确的航班延误情况预测结果;但是对延误航班的天气数据考虑并不全面。Choi等[8]针对气象数据,提出基于机器学习的航班延误分类预测模型;李晓霞等[9]考虑机场实际运行环境,利用聚类分析方法划分延误变量区间,结合贝叶斯网络建立延误预测模型,模型计算的准确性稳定在81.7%左右;王春政等[10]针对航班运行数据与气象数据,建立基于Agent 模型的机场网络延误预测模型。当对航班相关数据进行全面考虑后,处理航班数据样本问题时就会变得非常复杂。故Khanmohammadi等[11]在提取多变量特征与分析航班延误原因的基础上,建立基于多输入层人工神经网络航班延误预测模型;吴仁彪等[12]在融合航班数据与气象数据的基础上,通过加深网络的卷积神经网络构建航班延误预测模型,取得92.1%的预测精确度,提升了处理大样本与多变量数据的特征提取能力;可见在考虑结合气象数据等复杂多变量问题上神经网络更具有优势,但是模型精确度提升仍然受限。另外,单一航班串信息数据[13-14]在预测模型中的使用,并不能够反映真实航班之间关系,延误航班之间亦是如此,为让预测结果更加具有实际意义,故加入能够反映航班之间网络关系的航班网络数据,即增加航班网络结构。
因此,本文针对上述航班延误预测模型的研究与存在问题,在考虑航班信息、机场气象、航班延误历史的基础上,增加反映航班信息关系的航班网络结构,提出了一种基于深度全连接神经网 络(Deep Fully Connected Neural Network,DFCNN)的离港航班延误预测模型,并进行不同条件下的实验。该预测模型在全面考虑延误预测多项数据项变量的基础上,通过改进DFCNN 结构与调控模型参数,能够抑制梯度弥散现象,优化模型计算能力,取得更佳预测效果。
1 深度全连接神经网络与模型平台搭建
全连接神经网络(FCNN)作为深度学习(Deep Learning)的主要表现形式之一,以人工神经网络作为基础,包含输入层、隐含层以及输出层;FCNN 的连接通路能够连接上一层与下一层的神经元节点,利用BP 训练算法,让FCNN 展现出更佳的非线性表现能力;从FCNN 的结构来看,提升神经网络的表现能力主要有两种方式,分别为增加每一层神经元节点数量的横向拓展方式与增加神经网络层数的纵向拓展方式[15];而DFCNN 是在FCNN 中设置多个隐含层,即通过纵向拓展方式来组成深层的全连接神经网络,获得较多表现性能,来纵向增加和改进神经网络结构,并在实验中验证增加神经网络隐含层层数的效果。
然而,由多层隐含层组成的DFCNN 模型在计算过程中易出现过拟合现象,在训练过程中加入有着弱化过拟合能力的随机丢失层Dropout,可随机停止部分隐含层神经元,避免某些神经元的共同激活,并通过调控Dropout 参数值对模型进行优化[16]。再者,为加快计算过程中数值结果的收敛,在输入层、隐含层、输出层及各层之间添加激活函数,同时起到抑制梯度弥散的作用;其中,模型结构参数具体设置将在3.2 节中说明,以1 层隐含层为例,如图1 所示。
2 航班延误标准设置
旅客群体对航班延误最直观的感受是对航班实际起飞(实际离港时间)时间的感知,过长的延误时间易引起旅客积聚并造成拥挤现象,从而导致旅客单体或群体情绪的负向变化[17]。根据文献[18]中对不同延误等待时间范围下拥挤可接受程度的调查与可接受程度回归公式可知:15 min~30 min属于接受状态,而超过30 min 则越倾向于不接受状态,当时间在60 min 左右或者超过60 min 时旅客已经处于非常不接受状态。另外,《华沙公约》《海牙议定书》和《蒙特利尔公约》相继更正提出过航班延误的定义[19-20],但是由于各国发展进度不同,定义标准仍然存在较大区别。本文不再对其定义展开过多讨论,引用文献[21]的航班离港延误时间计算标准:航班实际出港撤轮档时间T与计划出港时间T0之间的差值不少于15 min,即T-T0≥15。
因此,针对旅客群体设置航班延误的时间标准阈值TH,选择15 min、30 min、60 min 三个阈值来判断航班是否延误。
3 本文模型
基于DFCNN 的离港航班延误预测模型的计算流程如图2 所示。
3.1 数据预处理
航班延误预测的研究对象一般是进港航班或离港航班,实验现有数据为成都双流机场(ZUUU)2017 年6—8 月与2018 年1—8 月中离港航班数据与机场气象观测数据。本文采用的成都双流机场离港航班数据包括:航班信息数据、航班延误历史统计数据和机场气象观测数据,这些原始数据存在异常项与缺失项,需进行剔除与填补,例如取消与返航航班的数据、缺失数据值。
所以针对原始数据项,进行如下步骤的预处理工作。
1)选取原始数据中的航班信息数据项、机场气象观测数据项和航班延误历史统计数据项,并将其中的其他数据项剔除;针对取消航班数据,因航班未能执行,故不作为延误航班数据,在本文研究问题中将此类数据剔除。
2)通过整理数据得到三类数据集:航班信息数据Fm(m=1,2,…,14)、机场气象观测数据Wl(l=1,2,…,18)与航班延误历史统计数据Dn(n=1,2,3,4)。数据集内容为:
①航班信息数据Fm包括航空公司、航班出发日期、航班计划出发时刻、航班实际出发时刻、起飞机场、目的地机场等共14 项数据。
②机场气象观测信息数据Wl包括:时间、气温、露点、气压、能见度、云高、云量、风速、风向、特殊天气现象等气象数据,共计18 项。
③航班延误历史统计数据Dn包括由不同始发地机场至目的地机场之间由于航空公司原因、天气原因、空管原因及其他原因造成的延误次数占始发地机场由此种原因造成所有延误的次数的比值,共计4 项。
3)将气象数据中的天气现象组的数据转化为0 或1 的随机数,转化规则是:若存在此种天气现象则将数据置为1,否则置为0。
4)通过one-hot 独热编码的方法将航班信息数据Fm中的航空公司、机场、日期等离散数据项转化为二进制字符串数组。
5)航班网络数据N即航段序号数据,是指同一架航空器按照其离港航班执飞时间先后进行排序,得到的一列序号数据,每一架航班的N取值为{1,2,3,4}(在航班原始数据中已有)。在相同时段内航班执行的先后顺序会因为航班延误存在的累积效应,导致后续执行航班延误加重;为突出这种延误中的航班网络关系,在数据项中加入航段序号数据列,以更好反映航班网络的延误程度及其相互关系。
6)将四类数据Fm、Wl、Dn、N中的连续型数据进行标准化处理,如式(1)所示:
7)根据Fm、Wl、Dn与N之间的时空联系,采用文献[22]中数据融合方法对离港航班数据、机场气象数据这两大类数据集进行逐一比较匹配并按照本文第4 章实验的需要,得到数据集A1、A2与A3,数据融合步骤如下:
①输入数据集:航班信息数据Fm、机场气象观测数据Wl、航班延误历史统计数据Dn及航班网络数据N;
②四类数据集的时空属性匹配:航班信息数据Fm、机场气象观测数据Wl、航班延误历史统计数据Dn及航班网络数据N中年、月、日、离港时刻及离港机场等属性需逐一对应;
③输出数据集:数据匹配完成后得到156 801 条数据,并通过直接复制对数据集的总样本量进行丰富,得到输入数据470 403 条;经数据预处理后,对数据集进行划分得到如表1所示数据。

表1 成都双流机场离港航班实验数据信息Tab.1 Experimental data information of Chengdu Shuangliu Airport departure flights
按照表2 中组合方式划入数据集合A,分别得到数据集A1、A2、A3,并进行储存,如表2 所示,亦为本文实验需要的输入数据集合做铺垫。
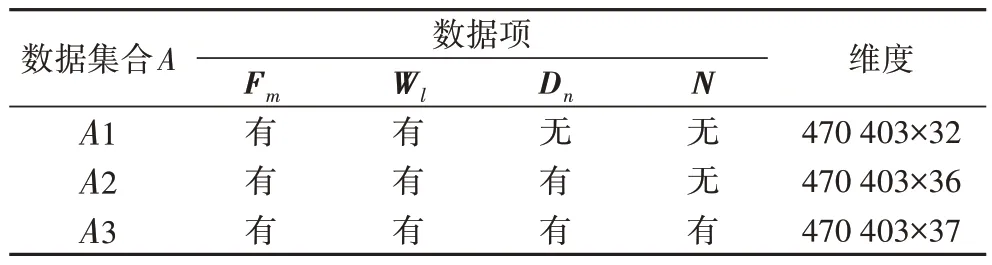
表2 融合数据项后的数据集合Tab.2 Datasets after merging data items
航班延误预测的最终目的是判断航班是否延误,属于判断为0 或1 的分类问题,可以将离港航班延误预测问题转换为式(2)形式:
即寻找航班信息数据Fm、气象数据Wl和航班延误历史统计数据Dn与函数f之间的关系,然后通过预设的阈值判断该串航班数据是否处于延误状态。
3.2 模型参数设置
基于DFCNN 的离港航班延误预测模型的关键要素主要包括神经网络层的设计、模型参数的设置和输入数据项,其中模型参数的设置主要考虑网络层之间激活函数、优化函数和损失函数等。模型通过损失函数(Loss Function)计算出预测值与目标值之间的误差值,利用反向传播算法原理和加速自适应梯度优化函数[23],在不断反向调整修正梯度参数与权值参数的计算过程中提高预测值的准确度。另外,深度全连接神经网络模型亦可看作复杂的线性拟合算法,但是数据集中的各项数值并不总是存在线性关系,激活函数的引入可以使得网络模型无限逼近任意非线性函数,从而获得数值间的非线性关系。
3.2.1 激活函数的选择
Sigmoid 函数、tanh 函数、线性整流函数(Rectified Linear Unit,ReLU)及指数线性函数(Exponential Linear Unit,ELU)等是常用的激活函数[24-25],这四种激活函数都有着能加速收敛和实现简便的优点,下面将展开详细讨论:
ReLU 函数是非零为中心的输出函数,具有稀疏表达能力,但是当输入值x为负值时容易出现梯度消失情况;而ELU 函数作为ReLU 函数的改进算法,避免了梯度消失的情况,当x为负值时能够获得一个自然梯度,但是其含有幂运算且计算强度较高。Sigmoid 函数经过演算推导变化可得到tanh 函数,它们作为激活函数在前向传播和反向传播的过程中计算得出数值项的方差值是近似的[26]。tanh 相较于Sigmoid 函数输出的均值更接近0,前者随机梯度下降速度能够更近似自然梯度,所以收敛速度会更快;Sigmoid 函数的线性区域会对较小的输入数据x产生聚集作用,会弱化层数的叠加意义;当输入x值较大时,x会在函数平滑区域聚集,梯度下降反而不利于收敛。因此模型的隐含层单元选择tanh函数、ReLU 函数和ELU 函数作为激活函数,并在4.2 节针对文章数据进行实验以获取模型最优的激活函数。
其中,经Sigmoid 函数算出的输出值能够准确落入(0,1),更好地表现二分类问题结果,因此选择能更好表现概率及受噪声更小的Sigmoid 函数作为输出层的激活函数。根据融合数据后的数据集合A设置神经元为512个,隐含层各层神经元为512个,其中最后一层隐含层为256 个。
其中:x表示输入值。
3.2.2 损失函数选择
损失函数能反映输入数据样本标签值与预测值的差异情况,交叉熵损失函数可表示已知数据值的真实分布与预测值分布之间的差异,降低交叉熵损失值(Loss)即减小输入真实值与预测值之间的差距,使得预测值逐渐逼近输入真实值,从而提高模型的精确度。可见平均交叉熵损失函数(式(7))对于度量分类问题中两个值的分布差异性有着明显优势。
其中:n表示样本个数;yi为第i个样本标签值;为第i个样本预测值。
3.2.3 随机丢失层Dropout的原理与设置
在神经网络模型前向传播时,通过设置随机丢失层Dropout 中每个神经元节点被停止的概率数值且有着相等的停止几率,使得模型不会太依赖局部特征,提高了模型的泛化能力,抑制过拟合现象。如图3 所示,以隐含层数为1 的神经网络为例,实线为工作的神经元节点,虚线为停止的工作神经元节点;有Dropout 层的神经网络计算公式,如式(8)所示:
其中:l表示神经网络的层数;yl为第l层输出值;f为激活函数;wl为第l层激活函数的权重系数;bl为第l层的偏置系数;rl服从伯努利(Bernoulli)函数以概率p的随机取值,在编码过程中能够以p∈(0,1)的概率停止部分工作的神经元节点。
故在本文4.2~4.5 节中设置Dropout 层默认p值为0.5 的实验,在4.6 节中增加不同p值的Dropout 实验,具体分析见第4 章。
4 实验与结果分析
本文预测模型代码采用Python 语言编写,在Tensorflow与Keras 深度学习框架下搭建;实验计算机硬件配置为Inter Xeon Silver 处理器,320 GB 内存,运行环境为64 位Windows Server 2016 版服务器。
4.1 模型结果评估
评估模型表现能力优劣最直观是预测结果中精确度(Accuracy,Acc)与损失值(Loss)的高低,输入标签值与预测值间的拟合度越高、精确度越高且损失值越小,证明模型表现能力越优异。损失值可根据3.2 中的损失函数得到,而预测精确度的计算将利用衡量分类模型准确度中最简便、直观的混淆矩阵(Confusion Matrix)方法。
航班延误预测结果的混淆矩阵表示有四种结果,对应情况如下:
1)真正例TP(True Positive):航班真实情况为延误,预测结果也为延误;
2)真反例TN(True Negative):航班真实情况为不延误,预测结果为不延误;
3)假正例FP(False Positive):航班真实情况为延误,预测结果为不延误;
4)假反例FN(False Negative):航班真实情况为延误,预测结果为不延误。
航班延误预测精确度PAcc是指正确预测航班的数量占总航班数量的比值,如式(9)所示:
4.2 不同激活函数的结果分析
在本文实验中,按照3.2.3 节中对隐含层的设置,隐含层层数设置为5,将输出层的激活函数设置为Sigmoid 函数,其他隐含层分别设置为tanh 函数、ReLU 函数和ELU 函数,Dropout层p值设置为0.5,延误时间阈值为15 min,实验输入数据集为A1。分别进行实验计算,以验证不同激活函数对模型表现能力的影响,得到图4 的损失值与精确度变化图。
实验结果表明:
1)从图4(a)可以看出,随着迭代次数增加,损失值逐渐收敛至固定区间;模型使用tanh 与ELU 函数的验证集与训练集的损失值差距较小且曲线变化稳定,取得较好的泛化性;经迭代计算ELU 函数在泛化能力上不如tanh 函数,但是模型稳定性好,两种损失值之间差距保持在0.20 个百分点左右,且迭代结果略优于tanh(如表3 中所示),说明模型拟合能力与泛化能力稳定;而使用ReLU 函数时训练集与验证集的损失值变化曲线差距较大,验证集的损失值变化波动较大,说明此时模型存在梯度弥散与过拟合。

表3 不同激活函数的实验预测结果Tab.3 Experimental prediction results of different activation parameters
2)从图4(b)可以看出,模型随迭代次数的增加,训练集与验证集的精确度逐渐升高并收敛至固定区间;使用tanh 函数在50 次迭代之后模型的泛化能力表现明显,并且经后续迭代计算两种精确度差距稳定在1.00 个百分点左右,说明模型拟合能力优异,有着较好的泛化性;在ELU 函数精确度变化中,两种精确度之差稳定在0.40 个百分点左右,证明模型拟合过程稳定且抗噪声能力优异;而使用ReLU 激活函数虽然在训练集上取得了较高的精确度且高于验证集精确度,相比之下其泛化能力与拟合能力较差。
3)如表3 所示,模型采用tanh 和ELU 函数计算测试集得到损失值与预测精确度分别稳定在0.218 6、0.216 2 和0.830 0、0.830 2,相较于使用ReLU 函数得出的结果在精确度上分别提升1.26 与1.28 个百分点。因此后续模型实验将以tanh、ELU 作为模型的激活函数,检验其结果是否存在偶然性。
4.3 不同数据项的结果分析
为验证航班历史与航班网络结构对模型计算的影响,针对不同输入数据项A1、A2、A3 进行实验;模型的隐含层层数设置为5,Dropout层p值为0.5,延误时间阈值为15 min,并在4.2 节的实验基础上分别对tanh 与ELU 函数进行数值计算;实验结果如表4 所示,在训练集和验证集上随着迭代次数的增加,损失值与精确度变化情况见图5~6。
通过对比不同输入数据的结果曲线变化图可知,模型在输入数据为A2(即对航班延误历史因素加以考虑)时,曲线变化波动比较平滑幅度变化相差不大,说明模型的拟合能力与表现能力变化不大;但是与输入数据集A1 相比,采用ELU函数与输入数据为A2 时模型损失值和精确度曲线图中训练集与验证集之间的变化差距更小,拟合效果略好;模型在加入A3 数据项(即在A2 基础上加入航班网络结构因素),在tanh 与ELU 函数模型的拟合表现能力上有着明显改善,模型的精确度能够稳定在85%以上,说明考虑航班网络结构能更好地反映航班间的延误关系,使得模型获得更好预测效果。
结合表4 中测试集的计算结果可知,在模型加入航班网络数据项后,模型收敛速度更快,能够在较少的迭代次数下实现较高精确度与较低的损失值,模型学习表现能力有着较大的改进;模型采用tanh 函数的损失值表现略好,但是ELU函数模型的预测精确度达到了0.861 3,相较于输入数据为A1、A2,分别提升了在3.11、3.12 个百分点;在航班延误预测问题研究中,在损失值较低的情况下,是以追求更高的预测精确度为目的,对航班延误与否做出更加精准的判断,综合4.2 节与上述实验结果与分析,结合ELU 函数的模型有着更好的优势,因此下文实验将使用ELU 函数进行计算,在航班网络结构的基础上进行研究。
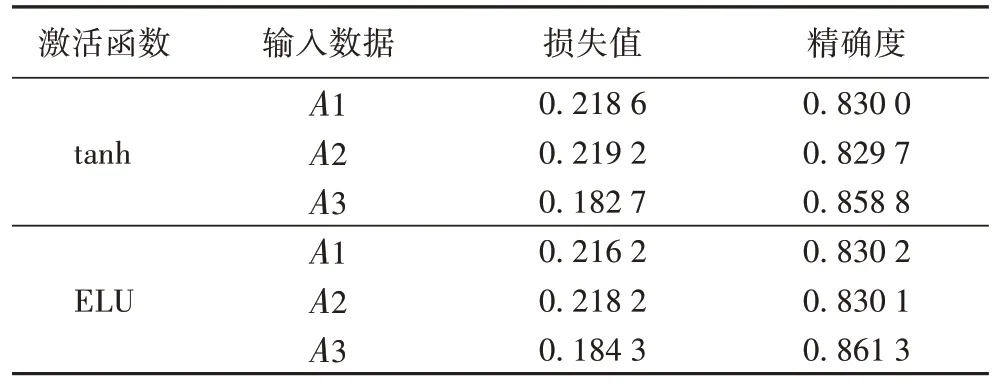
表4 不同输入数据的实验预测结果Tab.4 Experimental prediction results of different input data
4.4 不同阈值的结果分析
通过激活函数与输入数据项的实验分析可知,模型在激活函数ELU、隐含层层数为5、Dropout 参数为0.5 以及输入数据为A3 条件下能够取得可行性更高的实验结果;为期望实现在较长延误时间内的准确预测,在此增加延误时间阈值为TH=30 min,60 min 的实验。实验结果和迭代计算的变化情况如图7 与表5 所示。
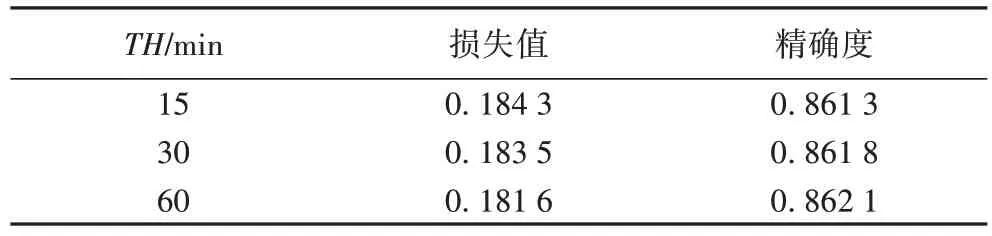
表5 不同阈值的实验预测结果Tab.5 Experimental prediction results of different thresholds
通过对比图7(a)中损失值变化曲线,随着延误时间阈值的提高,损失值的结果有着一定幅度的改善,在模型迭代计算50 次之前,随着阈值提高的训练集收敛速度最快,在局部放大图中损失值存在一定的波动,但是损失值的梯度变化效果明显。对比图7(b)中精确度曲线,可见随着延误阈值的提高,预测精度变化较为平缓提高,曲线变化拟合有所改善;在阈值为60 min时,比15 min 与30 min 的精确度分别提高了0.03 与0.08 个百分点,最终预测精度能够维持在86.21%。可见随着阈值的提高,对预测结果能够产生积极影响;在较大延误时间阈值下能够对长延误时间的航班做更好判断,在实际延误问题中有较高的价值。文献[27]中利用美国航班相关数据,建立相似的神经网络模型,经过500 次迭代计算获得91%以上预测精确度,可见使用不同数据集其预测效果仍有差别。
4.5 不同深度层数的结果分析
沿用4.4 节中实验的模型及输入数据条件,设定延误时间阈值TH=60 min,其中利用纵向拓展的方式改变神经网络的网络结构层次,检验对模型预测效果的影响,将DFCNN 模型中隐含层层数由5 分别增加至10 和15,进行不同层数DFCNN 的实验,实验结果如表6 和图8 所示。
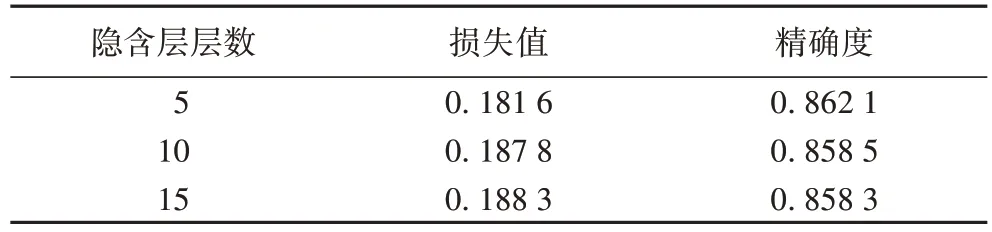
表6 不同隐含层层数DFCNN的实验预测结果Tab.6 Experimental prediction results of DFCNN with different hidden layers
由图8(a)可知,在模型迭代计算之初随着层数的增加,模型收敛速度变慢,损失值的训练集与验证集的曲线变化波动明显,易出现过拟合的现象;随着迭代次数的增加损失值逐步收敛,但是在较低层(5 层隐含层)时有着较好的表现。另外,由图8(b)可知,随着迭代次数的增加,精确度的梯度变化稳定且逐渐收敛;从局部放大图中可知,在较低层时的训练集与验证集的精确度较高,并且随着层数的提高在训练集与验证集上的精确度有着下降的趋势,说明模型拟合能力与泛化能力变差,存在梯度弥散的风险,可见单纯纵向拓展增加神经网络层次并不能直接改善模型的表现能力。
4.6 不同Dropout层参数的结果分析
经前文所做实验可知,深度全连接神经网络只在纵向拓展深度层次上不能更好地提高其表现能力,因此在前文实验的基础上加入Dropout 层参数的对比实验,在防止过拟合的同时,提升模型的泛化能力,并使用4.5 节中相同条件下构建层数分别为5、10、15 的DFCNN 模型。另外,对于工作的神经元节点不能过分保留或者停止其工作,故将p取值范围设置在0.3~0.7,间隔为0.2[28]。
通过对比表7 损失值结果与图9 各层数的损失值变化可知,随着p值的降低即随机停止神经元概率的降低,模型的损失值呈现逐渐降低的趋势,且在p=0.3 时降至0.109 3,相较于其他参数值下降明显,模型泛化能力更好;其次,通过局部放大图可知曲线变化平稳,未出现过拟合现象。
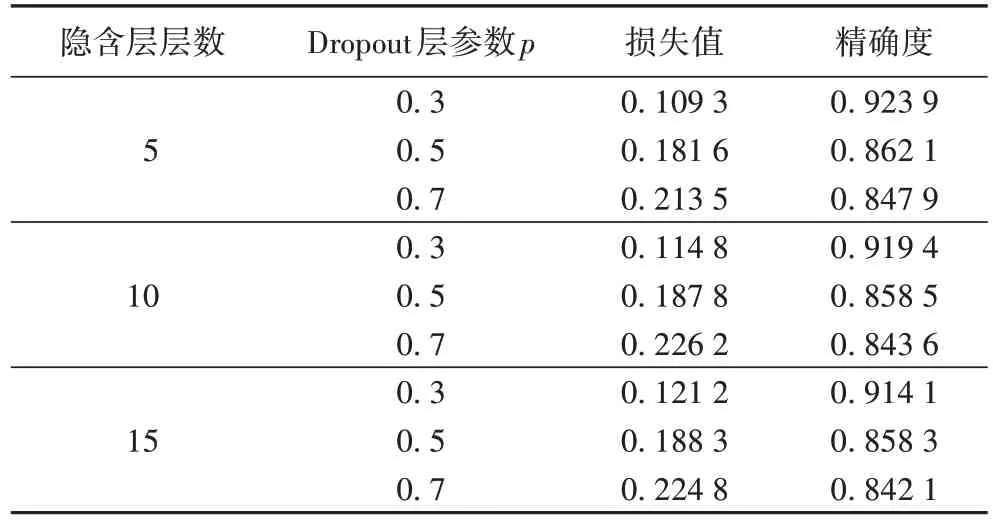
表7 不同层数下不同Dropout参数实验预测结果Tab.7 Experimental prediction results of different Dropout parameters under different layers
通过对比图10 各层数的精确度变化与表8 预测精确度结果可知,随着p值的降低即随机停止神经元概率的降低,模型在不同层数上都表现精确度逐渐提高,说明模型的泛化能力增强,梯度变化稳定,且在p=0.3 时精确度最高可达0.923 9,说明模型可靠性强和泛化能力优异。另外,通过对比不同层之间预测结果可知,随着层数的增加亦出现了4.5节中的相似结论。
4.7 不同航班延误预测模型对比
在前文模型实验的对比基础上,通过对比不同的二分类延误预测模型(决策树[29]、贝叶斯网络[30]、随机森林[31]、循环神经网络(Recurrent Neural Network,RNN)[32]、长短期记忆(Long Short Term Memory,LSTM)网络和人工神经网络(Artificial Neural Network,ANN)[33]的预测效果,说明本文延误预测模型在可行性与精确度上的优势,结果见表8。其中,文献[29-31]以国内航班相关数据为研究对象,模型具有简单快捷的优势;但是只有文献[31]对气象数据进行了全面的考虑,并且在计算分析复杂多变量问题上仍然受限,预测精度提升不明显。然后,文献[32-33]利用融合气象数据的美国亚历山大机场航班相关数据进行建模分析,在隐含层数为5,模型都取得较高的精确度充分证明了模型的有效性;但是在相同隐含层数下,本文通过改进5 层DFCNN 模型预测结果上泛化能力更强。

表8 不同航班延误预测模型预测精确度对比Tab.8 Comparison of prediction accuracy of different flight delay prediction models
综上所述,本文提出的改进5 层DFCNN 模型综合考虑A3 数据集中相关因素,模型预测精确度最高可达92.39%,能够为国内民航管制部门对航班延误提供更加准确的判断与参考。
5 结语
本文考虑激活函数、航班网络结构与时间阈值三方面影响的同时,对模型的神经网络层数与Dropout 层的设置进行了分析,得到结论如下:
1)通过融合航班信息数据、机场气象观测数据和航班延误历史统计数据作为输入项,并考虑不同激活函数的影响和采用ELU 函数,构建基于深度全连接神经网络的离港航班延误预测模型;在考虑增加航班网络结构后,模型的预测精度可以达到实际应用的精度,理论上可以较准确地判断航班是否延误,说明考虑
航班关系网络能够对模型有积极作用。
2)在实验过程中,随着网络层数的增加,模型出现梯度弥散与泛化能力变差,在实验迭代计算阶段甚至不如较低层数的网络模型,当隐含层为5 层时,预测精度可达86%以上。
3)在同网络层数上调整合适的阈值,可以对模型的预测精度起到积极作用,能够实现对延误时间较长的航班进行预测;加入Dropout 层后对隐含层神经元做适当取舍,在防止过拟合的同时,能够起到抑制梯度弥散与提升泛化能力的作用,最终预测精度在5 层DFCNN 时可维持在92%以上。
因此,本文的模型预测结果,可对国内航班延误做出较为准确的判断,给予民航相关部门提供可行的参考;在未来的研究工作中,不仅考虑纵向拓展对模型的影响,还要思考横向拓展各层神经元节点个数的配置问题与优化算法的研究。
