基于Weibull分布的沥青混合料疲劳性能分析

江照伟， 梁乃兴

(1.山东省交通科学研究院，山东 济南 250031；2.高速公路养护技术交通行业重点实验室(济南)，山东 济南 250031；3.重庆交通大学，重庆市 400041)

大量试验研究表明：沥青混合料的疲劳寿命具有很大的随机性和离散性，高离散性数据不利于疲劳性能分析的准确性[1]。如果要降低试验数据离散性对疲劳性能分析结果的影响，增大试验样本数量是一个有效的解决办法，但疲劳试验一般需要耗费很长时间，且沥青材料复杂的黏弹性特性决定了其疲劳性能影响因素较多，若要对不同工况下沥青混合料的疲劳性能进行全面研究，所需的试验成本将大大增加。受制于此，目前室内沥青混合料疲劳试验往往采用数量不多的若干试件进行。利用小样本试验数据较准确地分析沥青混合料的疲劳性能，需要借助统计分析方法和可靠性原理。

现有研究中通常采用正态分布或对数正态分布来描述疲劳寿命,凌丹等[2]利用Weibull分布对机械零件的疲劳寿命进行分析，认为Weibull分布对疲劳寿命数据的拟合能力优于对数正态分布和正态分布，并通过算例证明Weibull分布计算结果更符合工程实际；黎晓等[3]的研究结果显示：三参数Weibull分布函数可以避免在试验初始阶段进行疲劳失效概率的不合理估计，能更好地预估小子样条件下材料疲劳失效分布；黄琴龙等[4]在乳化沥青水泥稳定碎石疲劳性能研究中引入Weibull分布，研究结果证明材料疲劳寿命服从两参数Weibull分布，并建立不同失效概率下混合料的疲劳寿命预估方程；吴旷怀[5]等采用54条有效试件进行相同条件下大样本沥青混合料疲劳性能研究，结果显示沥青混合料的疲劳寿命呈三参数Weibull分布，三参数Weibull分布可以用于分析沥青混合料的疲劳数据。随着研究的深入，Weibull分布越来越多地被证明能够更合理地描述疲劳寿命分布。

该文采用间接拉伸法对AC-20沥青混合料进行疲劳试验，引入三参数Weibull分布对沥青混合料疲劳寿命进行描述，得到混合料在不同保证率下的应力疲劳方程，研究结果可作为不同保证率的沥青路面疲劳寿命预估的理论基础。

1 材料部分

1.1 沥青

试验采用中海AH-70#沥青，依据试验规程[6]对其进行检验，各指标满足规范[7]要求，主要性能指标见表1。

表1 AH-70#沥青主要性质指标

1.2 集料、填料

混合料所用集料为优质碱性石灰岩，填充料为石灰石矿粉。依据试验规程[8]对其进行检验，结果分别见表2、3。集料及填充料的性能均满足规范[7]要求。

表2 集料物理性能指标

表3 填充料物理性能指标

1.3 配合比

试验混合料类型为AC-20，配合比设计采用马歇尔法，图1为其合成级配图，最佳沥青用量为4.4%。

图1 AC-20合成级配图

2 间接拉伸疲劳试验

该文确定的疲劳试验方法为间接拉伸试验法，试验设备为UTM-100万能试验机，需配备高精度LVDT传感器，可以准确地测量试件的垂直总变形。

2.1 试件制备

疲劳试验进行之前需先测得AC-20混合料的劈裂强度，作为疲劳试验中不同应力比的调整基准。劈裂强度试验和间接拉伸疲劳试验试件均采用马歇尔试件，试件直径为101.6 mm，高度为(63.5±1.3) mm，劈裂强度试验平行试验试件个数为5个，疲劳试验平行试验试件个数为3～4个。

2.2 试验参数

2.2.1 劈裂强度试验

根据JTJ 052—2011《公路工程沥青及沥青混合料试验规程》[6]规定，劈裂强度试验加载速率为50 mm/min；分别在10、20、30 ℃3个代表温度下进行。

2.2.2 间接拉伸试验

试验采用应力控制进行；试验温度同劈裂强度试验；荷载为同温度下劈裂强度的0.3～0.6倍；加载波形为频率10 Hz的半正弦波；加载压条宽12.7 mm，试件预压荷载为20 kPa，预压时间30 s，使压条与试件充分接触；10、20 ℃以试件开裂，30 ℃以竖向变形曲线出现拐点作为疲劳失效判断依据[3]。

3 试验结果及分析

3.1 劈裂强度

根据10、20、30 ℃3个代表温度下劈裂强度的平行试验结果，以t分布法，得到AC-20沥青混合料保证率α=97.5%下的劈裂强度代表值，见表4。

表4 AC-20混合料劈裂强度

3.2 Weibull分布

Weibull分布于1951年提出，是根据最弱环节模型或串联模型得到的，能充分反映材料缺陷和应力集中源对材料疲劳寿命的影响，而且具有递增的失效率，将它作为材料或零件的寿命分布模型或给定寿命下的疲劳强度模型是合适的[9]。Weibull分布尤其对小样本抽样和各种类型疲劳试验数据有很强的适应能力。其概率密度函数[9]为：

(1)

式中：N为试验疲劳寿命；Na为特征寿命参数；b为形状参数；N0为起始最小寿命参数，N0可有效解决正态分布描述疲劳寿命分布时无法反映试件疲劳寿命大于等于零这一物理事实[10]，可以避免在试验初始阶段进行疲劳失效概率的不合理估计。

疲劳寿命n≤N的概率，即不可靠函数(失效率)为：

(2)

将式(1)代入式(2)，得到疲劳寿命分布函数：

(3)

则存活率函数为：

(4)

对式(4)两边取倒数后再取两次对数，得：

(5)

由概率分布理论，随机变量的破坏率遵循某一频率分布，不受抽样母体分布种类影响，小子样中某一样本xi破坏率的数学期望都可以用“平均秩”作为小样本母体存活率的估计量[11]。假设在不同温度应力疲劳试验中，某应力水平下获取了n个试件的疲劳寿命，将疲劳寿命按从小到大排列，对应第i个测定值xi的存活率R(N)估计量可用式(6)计算：

(6)

按式(6)计算存活率R(N)并选取合适的起始最小寿命N0，将其代入式(5)进行拟合，如果相关性良好，则说明Weibull分布适应疲劳试验数据。黎晓[3]的研究同时指出，基于试验结果获得的表征Weibull分布特征函数能较为清晰地描述不同沥青混凝土材料的寿命概率分布，能反映不同保证率下沥青混合料的疲劳性能。

3.3 疲劳寿命数据分析

表5为20 ℃时各应力比下AC-20沥青混合料的疲劳寿命。由表5可以发现：即使在同样的温度、同样的荷载条件下，不同试件的疲劳寿命次数相差很大，最大值与最小值甚至能达到10倍以上，再一次说明小样本的疲劳试验结果存在很大的离散性，在此情况下采用正态分布或对数正态分布对疲劳试验结果进行分析存在一定不准确性。

表5 20 ℃疲劳试验结果

由于篇幅所限，文中只列举20 ℃下的疲劳试验结果，以此为例进行沥青混合料疲劳性能分析。

假设沥青混合料疲劳寿命服从Weibull分布，令20 ℃各应力比下N0分别取300、500、1 000、1 000，按式(6)分别设定可靠度R(N)为80%、60%、40%、20%，代入式(5)，采用最小二乘法对表5中的数据进行拟合，发现相关性很高，说明沥青混合料疲劳寿命服从Weibull分布，同理可对10、30 ℃下的疲劳试验结果进行拟合判定，得到同样的结论。各工况下的拟合参数见表6。

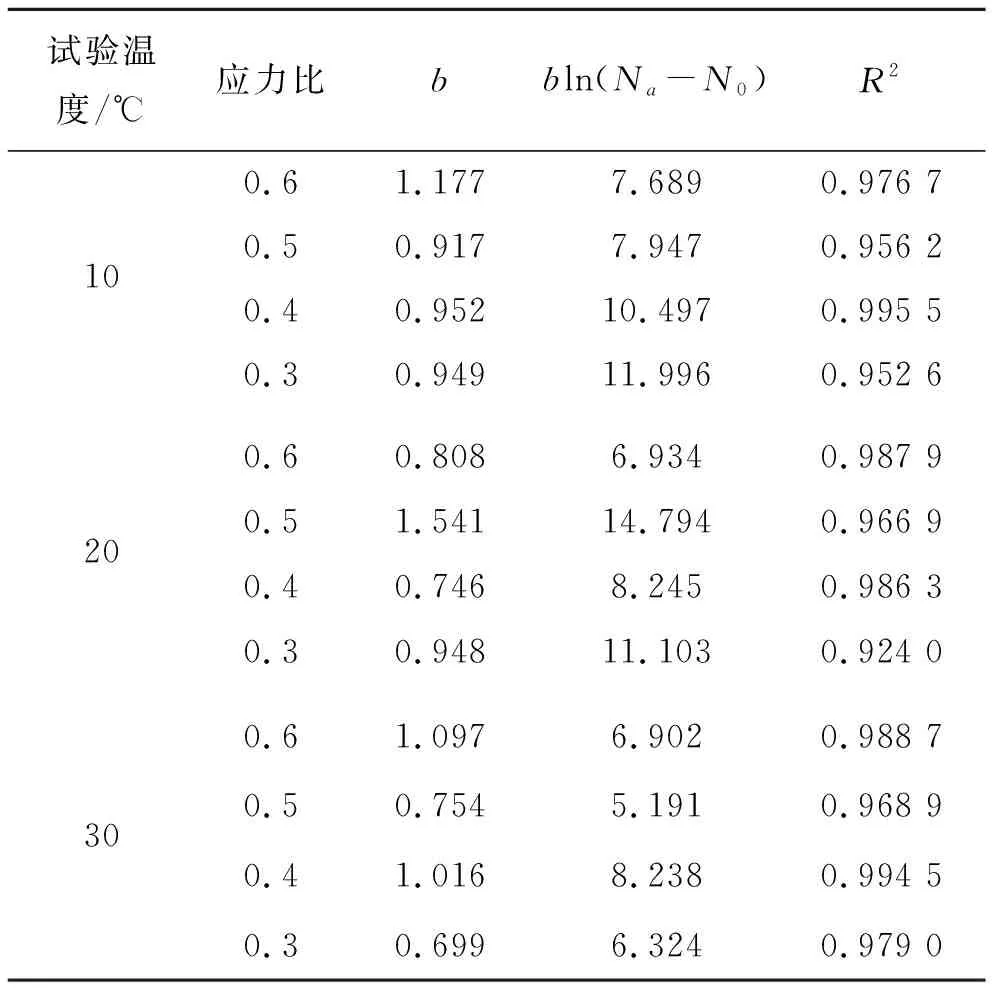
表6 疲劳寿命Weibull分布拟合结果

将确定的参数代回式(5)，则得到不同工况下混合料疲劳寿命Weibull分布方程，进而可以计算任意保证率下的目标疲劳寿命。现仅将20 ℃时AC-20沥青混合料在保证率50%、70%、90%、95%下的目标疲劳寿命计算结果列于表7。

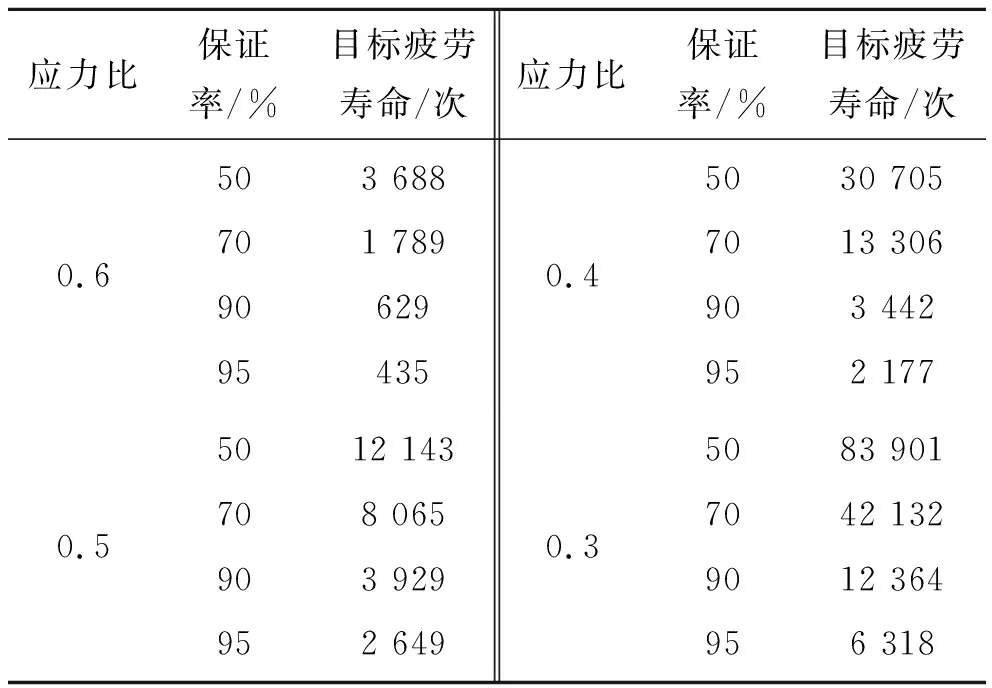
表7 20 ℃时不同保证率下目标疲劳寿命

3.4 疲劳寿命预估模型

由不同工况任意保证率的目标疲劳寿命，可以拟合得到AC-20沥青混合料不同温度任意保证率的应力疲劳方程。应力疲劳方程采用如下形式[12]：

N=kσ-n

(7)

式中:参数k、n具有明显的物理意义[13]，k值可表征混合料的抗疲劳性能；n值则可表征材料疲劳性能对应力的敏感度。

该文选择50%、70%、95%3个保证率，对AC-20混合料的应力疲劳方程进行拟合，采用双对数坐标，结果如图2所示。

图2 不同保证率、不同温度下的应力疲劳方程

由图2发现：不同温度下的应力疲劳方程有着明显的差别，随着试验温度的变化，k值和n值均明显变化，说明温度是沥青混合料的抗疲劳性能和应力的敏感性的重要影响因素。k值、n值与温度关系曲线如图3、4所示。

图3显示：不同保证率下的k值与温度呈现出高相关性的指数关系，混合料抗疲劳性能随温度的升高呈指数下降；低温时不同保证率下k值差异大，随温度升高，保证率对k值的影响逐渐减弱，可以预见，在30 ℃以上温度时，基本不受保证率影响，k值趋于一个与10 ℃k值拥有105的数量级差异的值。根据文献[14-15]，沥青混合料在周期性荷载作用下，疲劳损伤和蠕变损伤同时发生导致材料破坏，低温低荷载下疲劳损伤占主导，呈脆性断裂，高温高荷载下蠕变损伤占主导，累积变形造成破坏。综合分析后认为，k值在低温下可以有效描述和区分沥青混合料疲劳性能优劣，高温情况下由于混合料失效形式的改变，k值对混合料抗疲劳性能表征效果减弱。

图3 k值-温度关系图

图4显示：n值随温度的升高而减小，说明沥青混合料的疲劳性能对应力的敏感性随温度的升高而降低，10 ℃下沥青混合料的抗疲劳性能虽然优于其余两个温度，但应力变化会对其疲劳性能造成更大的影响。低温时沥青路面承受过多交变应力会加速疲劳失效。

图4 n值-温度关系图

对比图2同一温度不同保证率下的疲劳方程发现，保证率增大则目标疲劳寿命显著降低。提示在进行沥青混合料疲劳寿命预估时，应根据实际情况综合考虑选取合适的保证率[4]，若保证率取值过高，会导致材料疲劳失效判定次数过低，将造成材料性能的浪费；而保证率取值过低则会得到不安全的结论，可根据不同保证率设计需求选择对应保证率下的材料疲劳寿命分布。

4 结论

(1) 小样本试验条件下，沥青混合料疲劳寿命以很高的相关性服从Weibull分布，最小疲劳寿命参数N0的引入可有效解决其他方法描述疲劳寿命分布时无法反映试件疲劳寿命大于等于零这一物理事实，可以避免在试验初始阶段进行疲劳失效概率的不合理估计。利用三参数Weibull分布可以更为清晰地反映出沥青混凝土材料的寿命概率分布。

(2) 不同工况下的应力疲劳方程显示：随温度升高，沥青混合料抗疲劳性能呈指数下降，疲劳性能对应力的敏感性降低，沥青路面低温时承受过多交变应力会加速疲劳失效。

(3)k值-温度关系研究表明：随温度升高，k值将基本不受保证率影响，k值在低温下可以有效描述和区分沥青混合料疲劳性能优劣，高温时则失去上述表征效果。

(4) 保证率取值的大小决定材料疲劳失效判定次数的高低，保证率取值过高易造成材料性能的浪费，取值过低则易得到不安全结论，在进行沥青混合料疲劳寿命预估时，宜根据不同保证率设计需求选择对应保证率下的材料疲劳寿命分布，以在保证结论安全的前提下提高材料性能利用率。