考虑空间效应的大跨度斜拉桥随机地震下主梁力学响应规律分析

2022-11-08雷顺成刘国坤邓继华王祺顺

中外公路 2022年4期

雷顺成，刘国坤，邓继华，王祺顺

(1.湖南省交通科学研究院有限公司，湖南长沙 410014； 2.湖南工程学院，湖南湘潭 411104； 3.长沙理工大学土木工程学院，湖南长沙 410114)

随着斜拉桥计算理论的日臻完善、施工工艺及方法的不断进步，在中国跨江河地区获得广泛应用。但斜拉桥作为一种高次超静定的复杂结构，其受力状态呈现典型的空间效应，并且在地震、风等随机性较强的荷载作用下，其受力特征难以明确。目前，在斜拉桥等大跨径桥梁抗震分析中，为规避随机性荷载给分析带来的困难，大多数采用反应谱法和时程分析法两种手段，反应谱法作为一种静力模拟方法，可考虑结构各频段振幅极值，但是无法考虑地震随机性这一主要特点，且反应谱法仅适用于结构的线弹性工作状态；时程分析法基于分步积分的思想，可分析结构的最不利响应规律，同时可考虑结构进入弹塑性阶段后内力发生重分布变化的受力状态，是一种较为精确的地震效应分析方法，但是该法只适用于特定地震波形式，故以上两种方法均有明显的适用局限性[1-2]。为综合考虑地震波的随机性和多因素共同作用效应，该文采用绝对位移直接求解的虚拟激励法，以某特大跨钢箱梁斜拉桥为研究对象，探究大跨径斜拉桥在随机多维地震作用下结构力学响应特征，研究成果可为大跨径桥梁抗震分析及动力可靠度研究提供参考[3]。

1 虚拟激励法计算理论及方法

对于n个自由度、m个约束的结构，其线弹性运动方程可描述为：

(1)

式中：M、C、K分别为结构质量矩阵、阻尼矩阵、刚度矩阵；S和b分别为支撑约束和非支撑约束；Pb为3个方向的地震力矩阵向量；Xs为节点位移向量；Xb为地面强迫位移向量。

(2)

(3)

上述数学公式变换的物理意义为：对于某结构而言，在约束支撑位置施加一无穷大的质量块，可使得在约束位置的结构加速度响应值等于该位置地震效应实际加速度值。该法可通过求解约束处绝对位移的方式，有效解决有限元软件中无法对结构地震实际加速度进行精确模拟的问题[4]。

将式(3)代入式(1)并整理得：

(4)

假定约束处有某激励荷载，其表现形式为：

(5)

联合式(4)、(5)，整理可得：

(6)

若不计阻尼，则式(6)可简化为简谐振动运动方程式，通过对简谐运动方程式进行谐响应求解，即可得到响应功率谱矩阵。求得功率谱矩阵后，即可求得各阶振动谱矩阵和结构的峰值响应[5]。简谐运动方程和功率谱矩阵表达式如式(7)、(8)所示：

(7)

(8)

2 虚拟激励法在Ansys中的实现

由上述理论，通过在约束支撑位置施加质量无穷大的质量块，然后在约束位置施加X、Y、Z3个方向的激励荷载，将地震响应加速度等效为约束位置处的加速度响应值，即可实现Ansys对于虚拟激励法的模拟[6]。具体步骤如下：

(1) 建立实际结构Ansys有限元模型，在约束位置处施加质量为1×109的质量荷载，同时约束支点的转动自由度。

(2) 确定地震随机振动功率谱模型，确定模型参数。

(3) 确定相关函数模型以获取互功率谱密度，以便考虑地震行波效应、相干效应及场地效应。

(4) 构造三维虚拟激励荷载矩阵，并将激励荷载施加至有限元模型各支点约束上，调取Ansys谐响应分析模块，计算结构在各列虚拟荷载下的虚拟响应，求出虚拟响应曲线。

(5) 计算结构功率谱密度、各阶谱矩阵、响应均值及方差。

3 工程应用

3.1 工程概况

该文工程背景为某特大跨径斜拉桥，桥跨布置为(181.9+450+181.9) m，结构形式为双塔双索面钢箱梁，结构采用半漂浮体系。设计荷载为公路—Ⅰ级，主桥钢箱梁采用Q345qD钢材，桥塔材料为C50混凝土，斜拉索采用高强钢丝，标准抗拉强度为345 MPa。全桥分为17个吊装节段，索间标准间距12 m，加密区5 m。地震基本设防烈度为Ⅶ度。桥型立面布置图和截面示意图见图1、2。

图1 桥型布置图(单位：cm)

图2 横截面布置示意图(单位：cm)

3.2 有限元模型建立

使用Ansys/APDL建立该桥空间有限元模型，根据斜拉桥建模基本理论和桥梁本身特点，选用“脊骨式”建模方法，该法可较为精确地模拟闭口箱梁截面主梁的刚度和质量分布，使用Beam188梁单元模拟主梁结构，斜拉索采用Link10杆单元模拟，并使用弹性模量修正公式计入几何非线性的影响，在主梁和斜拉索之间建立MPC184单元模拟其刚臂，以保证桥面系的刚度都集中于中间主梁节点上。斜拉索初拉力以实常数的形式输入，在所有支撑约束位置均设置Mass21质量单元并施加大小为1×109kN的重力模拟无穷大质量块，以方便后续地震激励荷载的施加，有限元模型见图3。

图3 桥梁有限元模型示意图

4 结构自振频率分析

桥梁振动频率计算是抗震分析的基础，振动频率及振型能反映结构的刚度分布情况，为抗震计算提供依据。该文基于Block Lanczos法，计入大变形初始应力效应，提取斜拉桥前100阶振动频率，具体结果见表1。前6阶振型图如图4所示。

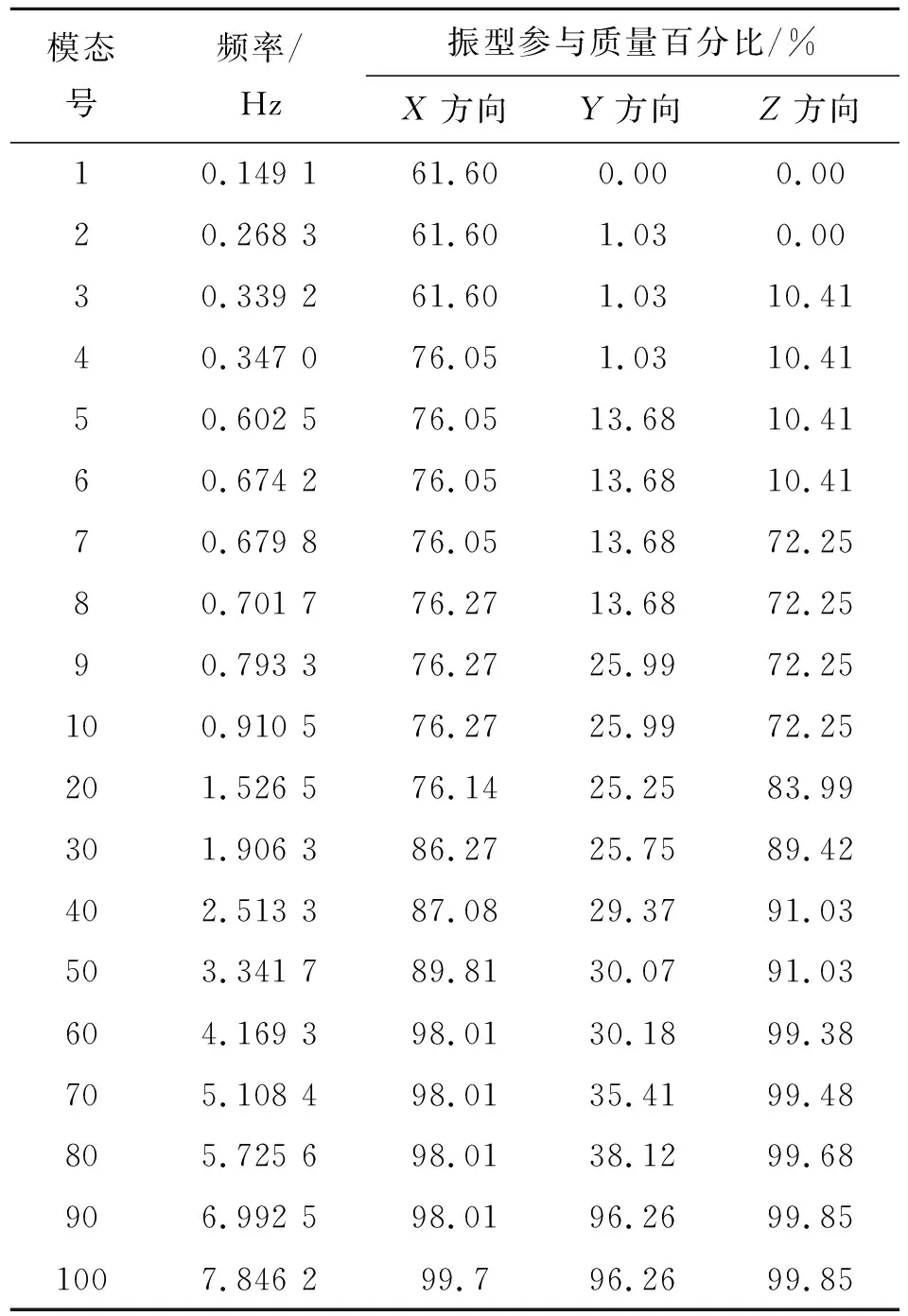
表1 前100阶振动频率及各方向振型参与质量比

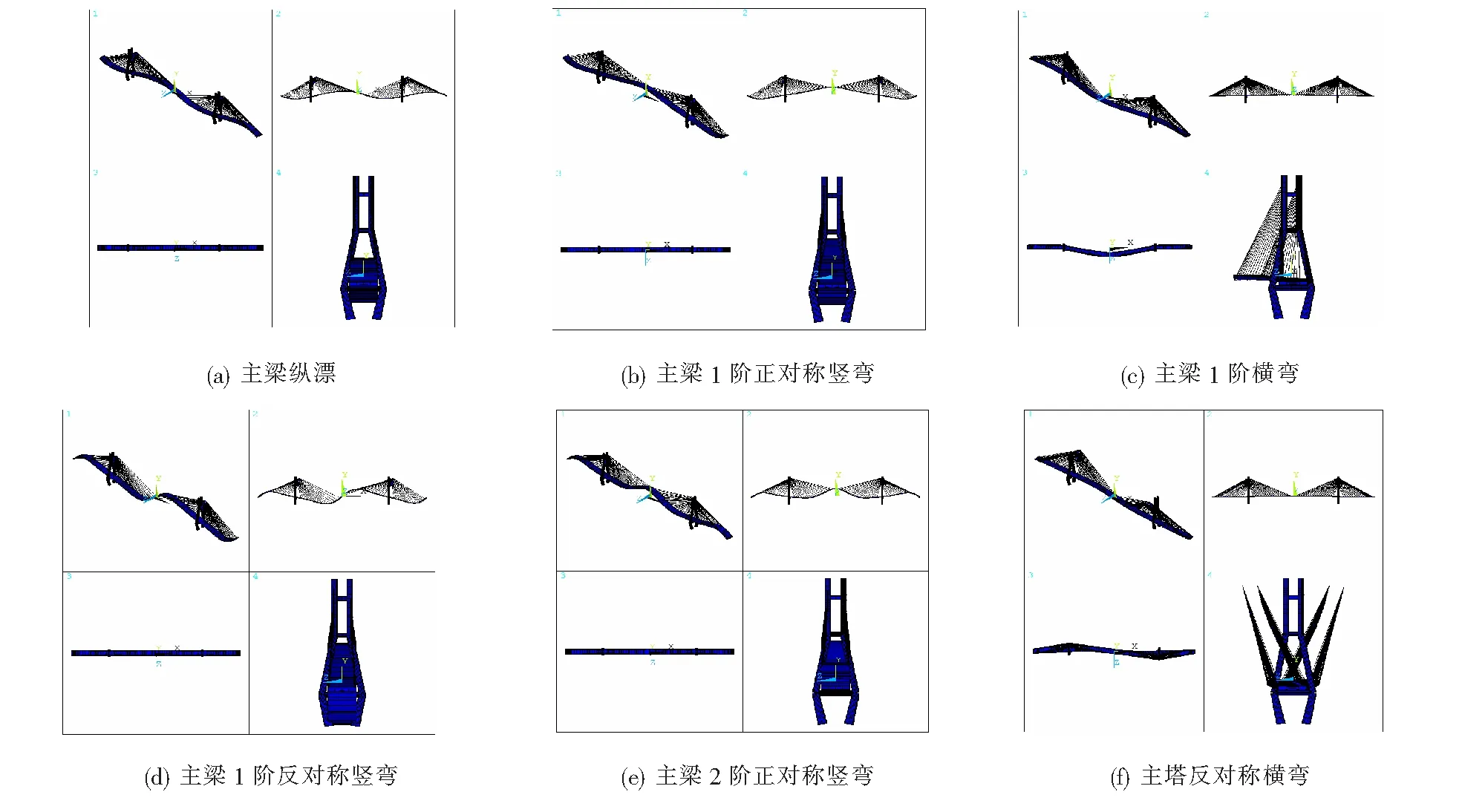
图4 前6阶振型示意图

表1表明：由于采用半漂浮体系，故自振频率较低，且在低阶模态区间频率分布较为密集，随着模态阶次升高，振动频率3个方向振动质量参与度越来越高，呈现出明显的三维耦合特性。由图4振型分析结果可知：主梁前3阶振型分别为主梁1阶纵漂、主梁1阶正对称竖弯、主梁1阶横弯，未出现扭转模态，说明结构具有良好的抗扭性能，同时，该桥主塔横向弯曲模态出现较早，应加强主塔横向抗弯刚度。

5 基于虚拟激励法的随机地震下桥梁空间力学响应规律

由前文桥梁振动频率计算结果可知，该桥振动频率小且低阶模态下频率分布密集，为克服低频成分的相互干扰，该文采用杜修力-陈厚群谱模型，该模型可克服结构低频能力过大或者存在奇异不收敛的缺陷，较好模拟地震效应的频谱特性。运用该模型分析斜拉桥在随机地震行波效应、相干效应和局部场地效应下结构力学响应特征[7-8]。

根据设计及勘察文件以及相关研究成果，选取以下参数作为模型输入参数[9]：白谱强度因子S0=17.26 cm2/s3，震源位置辐射加速度脉冲宽D=0.011 4，震源谱参数w0=1.83 rad/s，阻尼比ξg=13.03，场地土卓越频率wg=0.97 rad/s，平稳持时Tg=13.66 rad/s。X、Y、Z3个方向的加速度比值取为1∶0.85∶0.65，功率谱密度比为1∶0.722 5∶0.422 5，从而得到3个方向上自功率谱密度分别为：sox=17.26、soy=14.671、soz=11.219 cm2/s3。功率谱密度曲线如图5所示。

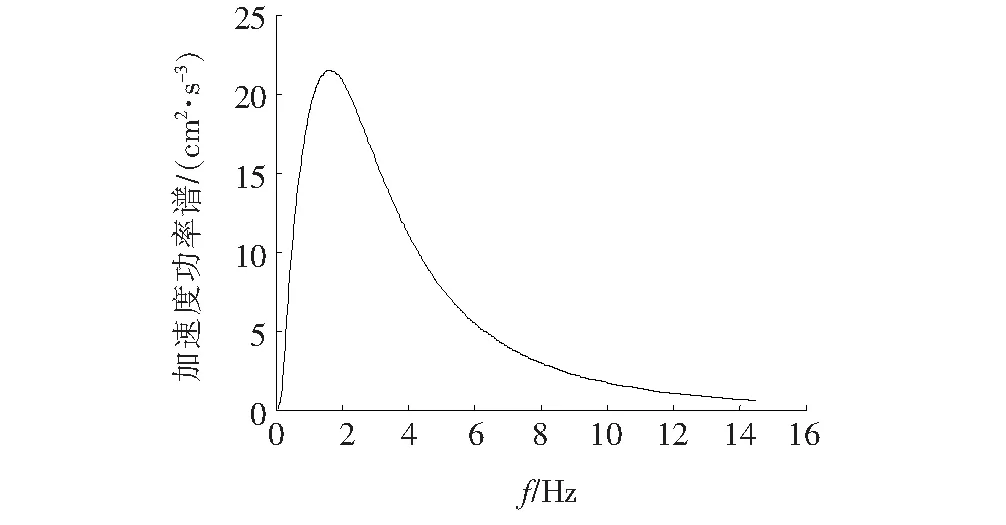
图5 功率谱密度曲线

5.1 行波效应

对于高次超静定结构的斜拉桥而言，行波效应的影响不容忽视，该文拟采用SMART-1台阵视波速表中第43号作为分析对象，见式(9)。选取v=1 000、4 000 m/s两组常量视波速和一致激励3个工况作为对比，提取主梁各物理量响应结果。

(9)

式中：c1、c2均为拟合参数，在43号地震中，其值分别为3 654和1 105。

图6、7为斜拉桥主梁在行波效应下弯矩、轴力、剪力及位移均方根响应结果。图6、7表明：考虑行波效应后，主梁弯矩响应规律与其他3种工况大致相同，但弯矩响应在波峰有一定变化且跨中位置弯矩不再为0；轴力与视波速之间敏感性较高，变化幅度剧烈；剪力变化幅度较小，仅在支座位置数值上有一定区别；主梁跨中位置竖向位移受行波影响明显。总体而言，行波效应对主梁内力及变形响应的影响并不是一致的，在顺桥向范围内，响应增大、减小或没有明显变化都有可能存在，而且响应特征受视波速影响较大，具有一定的复杂性。

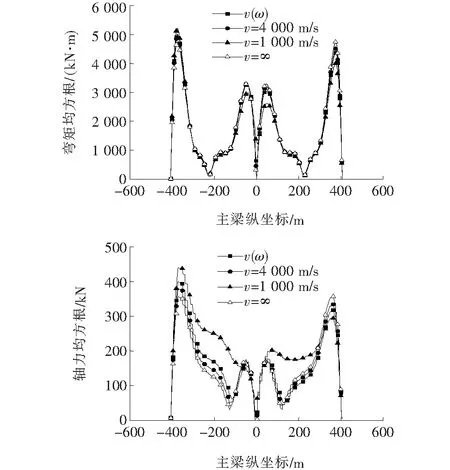
图6 主梁弯矩及轴力均方根

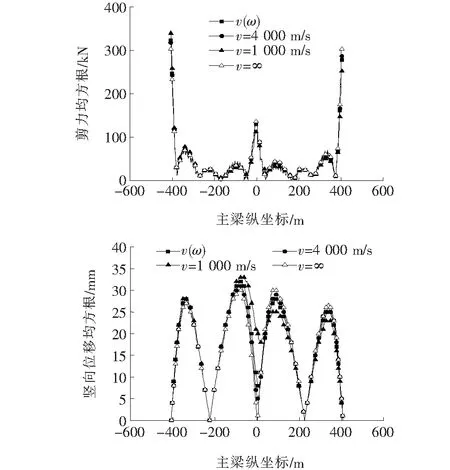
图7 主梁剪力及位移均方根

5.2 相干效应

选取QWW模型作为相干效应分析模型[10]，分别对比分析完全相干、部分相干、不相干3个工况下主梁力学响应特征。图8、9为相干效应下斜拉桥主梁弯矩、轴力、剪力及位移均方根响应结果。图8、9表明：主梁力学响应效应值与不相干程度有关，完全相干即为一致激励工况，部分相干工况效应值大于完全相干工况，但小于不相干工况，随着相干程度降低，主梁弯矩和位移减小，轴力增大，主梁剪力则没有明显变化，相干效应对结构在随机地震荷载作用下主梁力学响应特征是有利的。

图8 主梁弯矩及轴力均方根

图9 主梁剪力及位移均方根

5.3 局部场地效应

在分析大跨度桥梁随机地震动力效应时，应考虑局部场地效应对主梁的影响，基于虚拟激励理论，对比分析场地效应和一致激励下主梁力学响应特征。计算方法依据屈铁军提出的半经验公式[10-11]，见式(10)。其中土层覆盖厚度差值按Δh=5 m考虑，震中距差取两过渡墩间距Δx=632 m。计算结果见图10、11。

ΔS0=0.257 1Δh-0.012 4Δx

(10)