基于声发射和卷积神经网络的混凝土桥梁损伤预测研究

袁明， 王烁， 颜东煌， 刘昀,2， 黄练

(1.长沙理工大学 土木工程学院， 湖南 长沙 410114； 2.湖南交通职业技术学院 路桥工程学院，湖南 长沙 410132)

桥梁因长期暴露在外部荷载和不利的环境因素下，容易出现各种损伤和破坏[1-3]。桥梁裂缝宽度是评价混凝土桥梁损伤程度的重要观测参数。目前，各种无损检测技术已被成功应用于检测和识别桥梁结构的裂缝[4]，例如，视觉检测、数字图像关联技术(DIC)[5]、带摄像头的无人机(UAV)[6]和声发射技术(AE)[7]。其中，声发射技术是一种新型的动态无损检测技术，可以接收结构内部释放的微弱应力波，并将其转化为电信号进入系统进行处理。20世纪90年代就有部分国外学者发现声发射可以应用于混凝土桥梁结构的监控[8-9]。随着声发射技术的发展和完善，该技术的分析方法也在不断进步。此外，由于声发射技术在被动检测和综合监测能力方面的优势，它经常被用于实时损伤检测[10-11]。不少试验研究表明：不同的材料在外界荷载作用下，声发射信号会表现出不同的特征和趋势。因此，如何准确分析声发射信号，是研究声发射技术在桥梁损伤检测中的重要问题。目前常用的声发射信号分析方法包括特征参数分析法和时频分析法。Tonelli等[12]分析了负载下退役桥梁的声发射信号参数的特点；张艳博等[13]利用时频分析法研究了花岗岩的破裂过程；袁明等[14]提出了一种改进的损伤模型,采用三次多项式模型建立声发射参数与应力水平之间的定量关系，从而推导出混凝土梁的损伤演化方程，并从试件与构件层次采用3种损伤模型对损伤量进行了计算。然而这些关系都是经验性的 。到目前为止，声发射事件数与混凝土的损伤程度还没有建立起一个基本的理论关系，似乎这种关系并不存在[15]。在混凝土桥梁损伤识别的实际应用中，信号存在噪音多、损伤状态复杂、数据量庞大等问题，这些制约着声发射技术在实际工程中的应用。并且，目前现有的声发射信号处理方法过分依赖于先验知识，不同的材料和结构需要不同的先验知识才能完成损伤预测。

近年来，人工智能算法(AI)和有限元建模(FEM)被广泛用于分析和预测结构损伤的形成和扩展[16-19]。王岩等[20]利用BP人工神经网络和声发射技术有效预测和识别了混凝土的损伤程度。然而，传统的人工神经网络仍然需要先验知识，例如需要知道哪些声发射特征参数是神经网络所敏感的。相比较于BP人工神经网络，卷积神经网络(CNN)是一种更为有效的人工智能算法，它能够学习更为复杂的输入和输出关系。张瑞程等[21]提出基于一维卷积神经网络的燃气管道故障诊断模型，提取了原始声发射信号特征参数，能有效诊断燃气管道故障；董靖川等[22]利用分布式的卷积神经网络对刀具的磨损程度进行预测，其提出的卷积神经网络以原始波形作为模型输入，相比较于传统的BP神经网络，性能提高了51.3%。卷积神经网络的输入由于可以是整个信号波形或者是它们的转换，而不是从信号中提取出某些特征参数，意味着卷积神经网络有着更强的映射能力。基于此，该文将结合声发射和卷积神经网络对混凝土结构损伤程度进行识别和预测，这对结构状态预警及结构服役安全具有重要意义。综上所述，该文旨在开发一种更有效的桥梁结构损伤预测方法，该方法是将声发射技术与卷积神经网络(CNN)算法相结合，并通过斜拉桥模型进行试验验证，以说明该方法的有效性。此外，该文还将具体讨论卷积神经网络的架构设置，并与传统的BP神经网络性能进行对比。

1 损伤预测方法

图1为基于卷积神经网络与声发射技术的损伤预测方法的技术路线。首先利用声发射采集系统获取桥梁破坏过程的声发射信号，然后利用小波分解算法获取波形信号的二维时频域分解图，将分解完成的信号输入给已经完成训练的卷积神经网络并完成预测结果。该文采用王岩等[20]利用BP神经网络预测混凝土结构损伤程度中的分类方法，具体分类情况如下：轻度损伤对应0%～40%极限荷载；中度损伤对应40%～75%极限荷载；严重损伤对应75%～100%极限荷载。

图1 基于卷积神经网络与声发射技术的损伤预测方法技术路线

1.1 声发射技术原理

基于声发射技术定位方法的原理如图2所示。损伤产生的微振动将以应力波的形式传播一段距离，然后到达材料表面，在材料表面引起位移。声发射传感器检测到该位移并将其转换成电信号。之后，该信号被前置放大器放大，然后被过滤器过滤，并被A/D转换器捕获。最后，它被传输到数据处理系统进行分析和处理。

图2 声发射技术原理简图

1.2 卷积神经网络架构

图3为卷积神经网络的训练过程。首先，需要搭建适合于损伤预测任务的卷积神经网络模型，该文采用的CNN由卷积层、池化层、全连接层和一个SoftMax层组成。图3简单描述了该文所使用的卷积神经网络架构，其超参数设置如下：卷积层的核大小为3×3，步长为2，池化层的池大小为2，激活函数使用ReLU函数，优化器为Adam优化器，学习率为0.000 1。后文即是基于这种典型的CNN结构。每个特征图由多个神经元组成，每层的特征图作为下一层的输入。卷积层的特征图与上一层的特征图相关。为了保持主要特征并减少下一层的神经元数量，应用了池化层。

图3 卷积神经网络架构

1.2.1 卷积神经网络输入模式

为了捕捉声发射信号的多模态和色散特性以及混响特性，在连续小波变换的基础上进行了时频分析，并将其作为卷积神经网络的输入。f(t)为声发射波形。

L2(R)空间中的f(t)函数在小波基下被展开，这种展开被称为连续小波变换。 连续小波变换的定义为[26-27]：

(1)

式中：a为比例因子；b为位移因子。在该文中，比例因子为频率参数，位移因子为时间参数，所以一维的声发射信号一经连续小波变换，就意味着将一个时间函数投影到二维的时间-频率相平面上。此外，ψ*(t)为母小波；*为复数共轭。

该文使用的母小波是Morlet小波，其表达式为高斯包络下的单频复数正弦函数：

(2)

式中：C为重构中的归一化常数：

(3)

数据格式为1×1 024的波形信号经过连续小波变换后变换成二维的256×256的二维矩阵，随后送入卷积神经网络进行训练。

1.2.2 卷积神经网络卷积层设置

卷积层中每个神经元的输入来自上一层特征图的固定区域的神经元，其大小由卷积核的大小决定。卷积使用权重矩阵ωu,v进行计算，通常被称为核，其通过反向传播算法训练。卷积层的数学表达式如下：

(4)

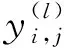
1.2.3 卷积神经网络池化层设置

池化层模拟了复杂的细胞过程，将初级视觉特征过滤和组合成更高级、更抽象的视觉特征，该功能在网络中通过采样实现。池化层采样后，输出特征图的数量不变，数据格式大小变小，有利于降低计算复杂性和抵抗小位移变化的作用。该文所采用的池化层的最大采样尺寸为2×2，即把输入的特征图分成一个个2×2大小的矩阵，不重叠。每个矩形取最大值，这样输出特征图的长度和宽度就是输入特征图的一半。在该文中，池化层的数学表达式为：

(5)

1.2.4 卷积神经网络全连接层设置

为了增强网络的非线性映射能力，同时限制网络的大小，在卷积层中提取特征后，网络被插入全连接层中。该层中的每个神经元都与前一层的所有神经元相互连接。其数学表达式为：

(6)

2 部分预应力混凝土斜拉桥损伤模型试验

2.1 声发射参数设置

试验使用声学物理公司(PAC)的Micro-2 Samous数字声发射系统仪器。该损伤试验中声发射仪器设置参数如下：阈值为45 dB，测试的采样频率为1 MHz。波长采样长度为1 k(1 024)，前置放大器增益为40 dB，峰值识别时间被设定为250 μs，冲击识别时间被设定为500 μs。该声发射仪器通过附着在试验梁上的传感器来捕捉损伤产生的波形信号，然后通过自编写的LabVIEW程序输出各个波形信号。每次构件振动产生的声发射信号(1×1 024)经过小波分解(256×256)后送入编译好的卷积神经网络架构训练，最终给出训练完成的卷积神经网络模型。在该文中，为了捕获混凝土损伤信号的多模态和色散特性以及混响特性，将波形信号进行小波变换[23-25]作为卷积神经网络的二维时频域输入。

2.2 试验模型及数据集划分

以某PC斜拉桥为工程研究背景[28]，并根据相似性原理，确定了1∶7.42的斜拉桥缩尺比例。如图4(a)所示搭建斜拉桥模型，通过布置在斜拉桥模型跨中腹板上的声发射探头[图4(b)]采集损伤过程中产生的声发射信号。试验采用车道荷载对试验梁加载，标准车道荷载包含均布荷载和一个集中荷载。表1为分级加载试验方案[29-30]。分级加载试验重复进行3次，均加载至7.49倍活载，并实测出试验梁最大裂缝宽度为0.53 mm。图5为3次加载试验的跨中位移的滞回曲线，其中跨中位移已经消除了支座位移的影响。

图4 PC斜拉桥模型静载试验

表1 分级加载试验方案

由图5可知：第1次加载试验后的残余变形达到7.63 mm，说明构件已经进入塑性工作阶段。为了确保试验安全，并没有继续加大荷载至完全破坏，而是将7.49倍活载作为构件正常使用的极限荷载。

图5 3次加载试验的滞回曲线

表2为3次试验采集的样本数量。3次试验所采集的数据分别编号为C1～C3，其中C1、C2组数据将用于卷积神经网络的训练，C3组数据用于评价该方法的性能。

表2 声发射信号样本数量

3 试验结果及分析

3.1 预测准确率

在利用C1、C2组试验数据完成对卷积神经网络的训练后，将C3组试验数据作为测试样本送入训练好的卷积神经网络，让其对每个信号所处的损伤程度进行预测分类，并将其与真实的损伤程度分类进行对比，将正确预测的样本量除以总测试样本量得到该方法的预测准确率。表3为C3组数据中不同损伤阶段信号的预测准确率，轻度、中度和严重的预测准确率分别达到了95.18%、97.99%和96.45%。值得注意的是，卷积神经网络仅学习了C1、C2组试验数据，在预测C3组时便能将误差控制在5%以内，说明该方法可以用于该部分预应力混凝土斜拉桥模型损伤试验的损伤程度预测。

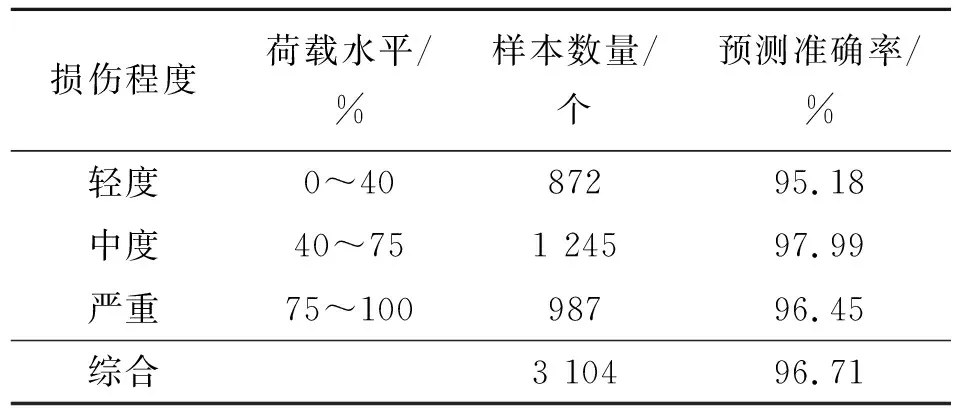
表3 预测C3组信号损伤程度的准确率

尽管该方法的损伤预测非常准确，但不可避免会将极小一部分的信号误判成与实际情况不相符的损伤阶段。分析产生“误预测”的原因主要有：① 现有的深度学习算法都存在性能上限，其根本原因在于训练样本与测试样本做不到完全的“一致”，C1、C2与C3组声发射样本数据并不是在完全相同的工况下获取的，尽管加载工况是一致的，每一次加载试验梁损伤会得到积累，而且加载进程会存在一定程度的随机性。因此这种原因带来的误差不可避免；② 各种损伤阶段的划分是一种人为手段，但是混凝土的损伤开裂实际上是一种连续演变的过程，处在两种损伤阶段界限附近的信号会有极大概率会被卷积神经网络误判成“相邻”的损伤阶段。

3.2 卷积神经网络架构对损伤程度预测结果的影响

针对不同的应用，卷积神经网络的架构是影响其预测准确率的一个重要因素，它们之间主要的区别在于卷积层与全连接层的数量多少。不同卷积神经网络下的预测准确率如图6所示，图中C和D分别为卷积层和全连接层数，例如2C-2D代表两层卷积层加上两层全连接层。

由图6可知:在3种不同的损伤阶段中，2C-2D的卷积神经网络架构的准确率更高，表明其更适用于该应用。在所有参与测试的架构中，构造最复杂的5C-5D网络架构比准确率最高的2C-2D网络架构低6%～8%，而简单的1C-1D架构的准确率仅比2C-2D低1%～2%。4C-4D的网络架构虽然对中度和严重损伤阶段信号的识别率较高，但是对数据量较少的轻度损伤信号识别较差，其综合性能不如2C-2D的网络架构。主要原因可能是不均匀的数据集划分对特定的网络架构的训练结果产生不利影响。另外，卷积神经网络的权值和阈值的初始值是随机产生的，因此网络架构的性能存在一定的随机性。 总体上可以发现越复杂的网络架构往往性能越差，而最简单的1C-1D的网络架构也有非常良好的识别准确率。

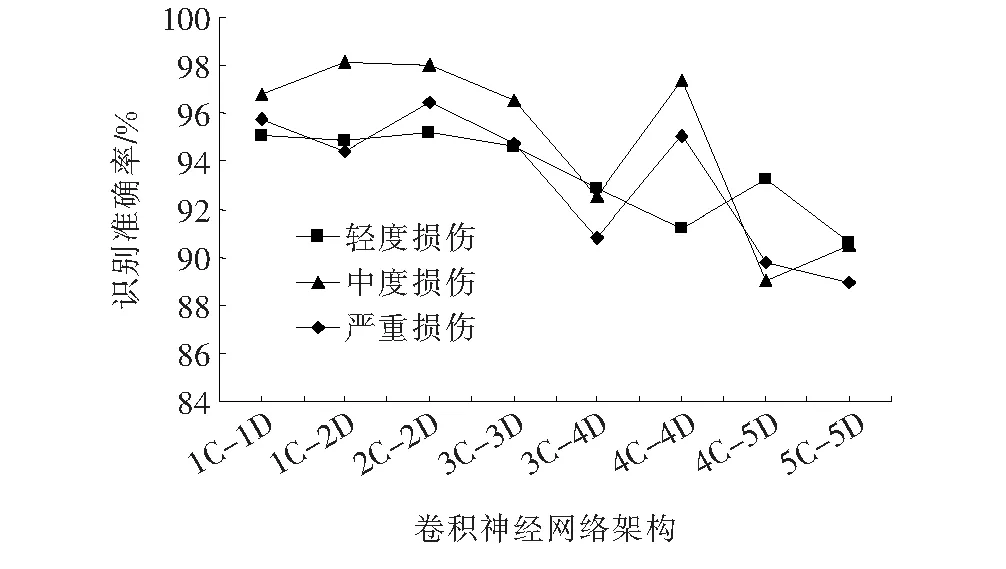
图6 不同卷积神经网络架构下损伤程度预测的准确率变化

在卷积神经网络的架构中，网络层数越多，网络的表现力就越强，即越能拟合复杂函数。然而，随着网络拟合能力的提高，该模型也容易出现“过拟合”，即在训练样本上表现较好，但在测试样本上表现较差。该文所描述的应用中，并不是更复杂的网络架构性能表现更好，更复杂的架构意味着网络本身更容易“过拟合”。对于简单的损伤分类任务，浅层的卷积神经网络往往性能优异，并且节省训练的时间成本。

3.3 BP神经网络预测损伤程度结果对比

已有研究表明[31]：幅值、振铃数、持续时间、能量、绝对能量及信号强度6个参数能够较好地体现混凝土损伤过程的阶段性特征，并且适用于BP神经网络来预测混凝土的损伤程度，所以该节采用BP神经网络的输入取这6个参数进行分析。BP神经网络的隐含层节点数是影响神经网络性能的关键，为了确定最佳的BP神经网络性能，对比了不同隐含层节点数下的BP神经网络性能，得到综合识别准确率分布如图7所示。当隐含层节点数为22时，BP神经网络的三阶段损伤程度综合识别准确率最高，为89.01%。表4为最优的BP神经网络(22节点数)与最优卷积神经网络(2C-2D)的具体预测损伤结果对比。结果表明：卷积神经网络的性能明显优于BP神经网络。其根本原因在于BP神经网络的输入仅有1×6的向量，卷积神经网络能够对256×256的二维矩阵进行训练学习，其带来的信息量的提升是非常巨大的。对于声发射信号而言，提取其特征参数尽管能够节省分析成本，但也意味着忽略掉了许多信号本身重要的信息，从而导致BP神经网络对损伤程度预测结果比卷积神经网络有所不足。

图7 不同隐藏节点数下的BP神经网络的准确率分布

表4 卷积神经网络与BP神经网络的性能对比

4 结论

针对采用声发射方法监测混凝土构件损伤程度的问题，搭建并训练适用于该应用的卷积神经网络，通过部分预应力混凝土斜拉桥模型损伤试验中轻度、中度和严重3类损伤信号验证了该方法的有效性。研究结果表明：

(1) 基于卷积神经网络与声发射技术可以很好地预测出混凝土的损伤，识别结构损伤程度，3 104个声发射信号的综合准确率高达96.71%。该方法能够在完全不需要先验知识的情况下完成损伤程度的有效识别，具有很强的泛化能力，并且有效提高了对混凝土构件安全性能的预警能力和综合判断能力。

(2) 在混凝土损伤程度预测应用中，预测效果最好的卷积神经网络是两层卷积层加上两层全连接层的网络架构(2C-2D)，相比较于5C-5D的网络，其准确率提高5%。说明浅层的卷积神经网络的性能更加优异，多层的卷积神经网络反而训练时间更长，损伤预测准确率下降。

(3) 在相同的数据集训练与验证情况下，对比传统的BP神经网络，卷积神经网络准确率高出5%～10%，并且能够对多维数的波形信号进行训练和识别，并不依赖于声发射信号特征参数的提取。