基于Simulink与COMSOL联合仿真的MOS场效晶体管瞬态特性分析

2022-11-07高兵王帅钟永恒孙雅森张尚琛周婕

湖南电力 2022年5期

高兵，王帅，钟永恒，孙雅森，张尚琛，周婕

(1.湖南大学电气与信息工程学院，湖南长沙 410012；2.国网湖南省电力有限公司电力科学研究院，湖南长沙 410007)

0 引言

随着新时代的发展，电力电子技术的应用领域越来越广泛，在直流输电系统、无人驾驶汽车中都有所应用[1]。如此广泛的应用领域对电力电子器件的性能、可靠性、安全性、经济性提出更高的要求。相关研究表明，功率器件作为变流器的核心部件，其失效概率占变流器故障原因的50%以上[2]。因此，对功率器件的特性进行研究分析，从而对其运行状态进行监测与评估，进而预测器件的故障状态，可以在一定程度上避免故障的发生，减少不必要的损失。相比于传统单一尺度的仿真分析，多尺度结合仿真所反映的信息更加全面[3]，也能够更有效地对器件特性进行分析。

目前的研究通常以实际中常用的功率MOS场效晶体管(metal-oxide-semiconductor field effect transistor，MOSFET)与绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)为实验对象，研究内容主要集中于器件的失效特性、多场耦合分析、开关特性、多尺度建模等。文献[2]以功率MOSFET为实验对象，使用COMSOL软件建立了高还原的电—热—力三场耦合有限元模型，并使用该模型针对器件的多种失效模式进行稳态分析，通过搭建实验平台验证了模型的可行性。对于功率器件的开关特性，通常建立含有寄生电容等主要参数影响的开关电路模型，并常将开关过程分成4个小阶段进行特性分析。文献[4-9]建立了包含寄生电容、寄生电感在内的MOSFET开关电路模型，并以此进行了多种状态下的开关特性分析。文献[10-11]将MOSFET的开关过程划分成4个小阶段，并对每个阶段的状态变化进行了详细分析。虽然开关特性分析能够较好地展示器件状态变化，但是无法揭示其他物理量的变化过程，因此多物理场、多尺度建模很有必要。文献[12-14]基于Simulink软件建立MOSFET的电—热耦合模型，结果曲线显示了更多更详细的物理量变化过程，但相比于专业有限元仿真软件，略有不足。文献[15]展示了一种多场耦合的有限元仿真模型，并以此分析了器件可靠性。文献[16-18]给出了多尺度电力电子变换电路的建模方法，并进行了验证。

本文以功率MOSFET为仿真对象，考虑开关特性和多尺度特征，选取导通电流和导通压降作为模型交互信息，建立开关电路和有限元联合仿真模型，并分析不同电流以及不同开关频率下MOSFET开关信息和宏观物理场信息交互的瞬态特性。

1 MOSFET开关电路模型

MOSFET是电压控制电流型器件，共有栅、源、漏三个电极，当器件栅极承受电压大于导通阈值电压时，漏、源极之间形成通路，电压电流波形随开关状态周期性变化，但是受器件寄生参数的影响，开关波形会发生一定畸变。为了研究器件的多种特性，建立了不同的分析模型。通常，采用如图1所示等效电路分析功率MOSFET的开关特性[11]，图中电路所包含的寄生参数有极间寄生电容、电极寄生电感、反向体二极管和栅极电阻。

图1 等效开关电路

依据图1在Simulink中搭建开关电路模型。软件中MOSFET模块的栅极是信号端口，无法和脉冲电压源的电路端口直接相连。考虑到MOSFET内部结构中栅极和漏、源极之间绝缘层不导通，因此，结合Simulink的特点，将MOSFET栅极的电路功能和信号功能分离。

对于信号功能，在模型中直接使用一个脉冲信号源P控制栅极；对于电路功能，将栅极电源线连接到栅—漏、栅—源寄生电容一端进行等效，且为了与分离出的栅极信号保持同频，在栅极电路中加入了一个由脉冲信号源P控制的理想开关s1，以此控制电路的开断。为了方便分析结果，在模型中采用直流电流源激励以及阻性负载。最终建立MOSFET开关电路仿真模型如图2所示。

图2 开关电路仿真模型

整个模型的开关频率及占空比可通过脉冲信号源P控制，现将其脉冲频率设置为1 Hz，占空比为50%，脉冲信号幅值为10 V。漏-源极激励电压VD设置为400 V，负载电阻RL设置为20 Ω。MOSFET导通压降设置为1.5 V。寄生电容、寄生电感等参数可参照功率MOSFET数据手册设置，并将模型仿真时长设置为3 s。

其中开关电压的仿真波形如图3所示，由于模型采用直流电压源和阻性负载，所以导通电流波形与开关电压波形除幅值不同外呈现关于时间轴对称特性。

图3 开关电压仿真波形

由图中开关电压曲线可知，在秒级尺度，器件在开通过程中(1.1 s)的波形有明显尖峰，关断过程中(1.5 s)的波形没有明显变化，整体与理想波形基本一致。但是在纳秒级尺度下观察，器件在开通过程中的电压具有波动性，关断过程中的电压具有一定坡度，与理想波形具有一定差别。

寄生参数的加入使得波形不再是理想波形，而具有一定畸变，这与实际波形更相近，为联合仿真模型提供了更精确的电流信息。

2 MOSFET电—热—力耦合模型

以型号为IXFK80N60P3的功率MOSFET作为研究对象，使用COMSOL软件构建有限元模型，模型如图4所示。为了保证仿真结果的准确性，利用功率器件分析仪和温度湿度振动三综合试验箱测量了器件在栅极电压为10 V的情况下，以每15℃、100 mA为阶段划分的-55～140℃、5～100 A范围内的芯片电阻值，并经过插值处理后将数据导入仿真模型中。其中仿真模型的尺寸和材料特性参数见表1和表2[2]。

图4 全尺寸有限元仿真模型

表1 功率MOSFET结构尺寸表

表2 功率MOSFET材料特性参数

器件在运行过程中会受到多个物理场耦合的影响，电流场会产生功率损耗，该功率损耗成为温度场中的热源，热源的变化导致模型温度波动以及分布不均匀，进而使模型产生形变，从而影响参数变化，因此必须考虑电—热—力耦合效应[19]。

MOSFET模型内部电流场的表达式为[20]:

式中，J为电流密度；γ为电导率；Qj为边界电流源。

器件中电流的流通产生功率损耗，该损耗成为器件内热源，使得器件温度上升。单位体积的功率损耗可表示为:

式中，Qv为单位体积内的焦耳热。

根据传热学理论，考虑物体内热源影响时，热传导方程[20]为:

不考虑物体内热源影响时热传导方程[20]为:

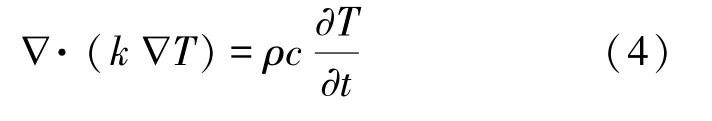
式中，k为导热系数，W/(m·℃)；T为温度，℃；Qv为单位时间内单位体积中的内热源，W/m3；ρ为物体密度，kg/m3；c为比热容，J/(kg·℃)。

由于器件多层结构间热膨胀系数的不匹配，器件在受热膨胀或变形时将受到约束，从而在器件内部产生热应力。根据线性热应力理论，物体的总应变由两部分相加组成，一部分由温度变化而引起，另一部分由应力引起[20]，如式(5)所示。

式中，εth为热应变，εE为应力应变；E为杨氏模量，GPa；u为泊松比；α为热膨胀系数，1/℃；T和Tref为温度和参考温度，℃。

基于上述控制方程，可在模型内实现电热力耦合。针对全尺寸模型瞬态计算存在计算资源消耗过大的问题，对多物理场有限元模型进行简化，主要思路包括两方面:其一，对模型结构进行规则化处理，主要包括螺丝孔、不规则铜层和曲形键合引线；其二，对网格单元剖分方式进行改变，将软件内置的“常规”剖分方式改为“极粗化”剖分方式，有效减少网格数量、增大网格单元。简化后模型如图5所示，网格剖分如图6所示。

图5 简化后有限元模型

图6 简化后网格剖分

为缩小模型简化所导致的数据误差，将简化后模型底面等效散热系数由5 000 W/(m2·K)改为3 800 W/(m2·K)，然后以不同初始导通电流(20 A、25 A、30 A)对模型进行分析。将简化前后参量数据根据相对误差计算公式(6)的相对误差，其计算结果见表3。

表3 模型简化前后多参量对比 %

分析表中数据可知，结温(Tj)相对误差不超过0.5%，壳温(Tc)相对误差不超过2%，导通压降(Vds)相对误差不超过1.5%，导通电阻(R0)相对误差不超过2%，焊料层最大位移(dis)相对误差较大，但也不超过20%。各个参量的相对误差都保持在一定范围内[21-22]，可认为本文所构建的简化模型能够较为准确反应MOSFET的耦合特性。

3 MOSFET的场—路联合仿真模型

基于上述模型，将开关电压和导通电流作为开关电路和有限元模型的交互数据，在Simulink中建立场—路联合仿真模型。将模型的整个仿真时长设置为30 s，考虑到整个仿真过程较长，因此将信息交互步长设置为0.5 s，即每半个周期交互一次，以缩短总体仿真时间。整个仿真流程如图7所示，是一种串行的仿真方式。

图7 联合仿真流程图

在开关电路模型中，功率MOSFET模块的导通压降是恒定的，无法表征温度对其的影响。而有限元模型可表征这一影响，因此在联合仿真模型的电路部分加入一个电压控制电压源，以此将有限元模型输出导通压降作为控制信息输入到电路部分，此时需要将MOSFET模块中的导通压降设定为0。

仿真中主要观测的参数为壳温(Tc)、结温(Tj)、芯片电阻(Rds)、导通压降(Vds)、焊料层最大位移(dis)、漏极电流(Id)。最终建立联合仿真模型如图8所示，可以实现MOSFET开关过程和宏观多场耦合模型的交互和计算。

图8 联合仿真模型

4 结果与分析

首先计算分析了在开关频率为1 Hz，占空比为50%情况下，初始导通电流分别为20 A、25 A、30 A时的MOSFET瞬态特性。

其中Id=20 A时开关电路模型和联合仿真模型电流波形对比如图9所示。

图9 导通电流波形

对比图中电流可以看出，联合仿真模型开关电流由于导通压降的变化及寄生参数的影响，具有一定的下降趋势和随机性，更能反应器件的开关特性及场耦合特性。

导通压降、芯片电阻、焊料层最大位移、壳温、结温参量的瞬态波形如图10所示。

图10 不同电流下各参量波形

分析图中各参量波形可以得知，随着初始导通电流的增大，各个参量的上升率、稳态值也随之增大，而且不同电流之间稳态值增加的幅度也逐渐加大。另外，结温、壳温、导通电阻值、焊料层最大位移这些随着开关状态周期性波动的参量，其周期内最大值与最小值均随着导通电流的增大而增大，且其波动程度也变大。

考虑到材料的传热系数具有一定的非线性以及各材料间传热系数不同，当电流改变时器件的热平衡状态也随之改变，因此出现稳态值以及波动程度变化的情况。

计算分析导通电流为20 A、占空比为50%时，开关频率为1 Hz和0.5 Hz时的MOSFET瞬态特性。部分参量波形如图11所示。

图11 不同频率下参量波形

对比图中开关频率为1 Hz与0.5 Hz条件下的器件瞬态参量波形，可以看出0.5 Hz下的导通压降幅值有所增大。另外，对于随器件开关转换而周期性波动的参量，其波动程度增大，但与同一频率下不同电流时的情况有所不同，0.5 Hz下开通状态内最大值大于1 Hz下最大值，关断状态内最小值小于1 Hz下最小值。分析器件的产热过程以及散热过程可知，频率变小时，器件热量积累以及热量损耗更多。