采用非线性无源理论的MMC–MG并网电流控制

王兴贵,王海亮,薛 晟,李晓英

(兰州理工大学电气工程与信息工程学院,甘肃兰州 730050)

1 引言

微电网(microgrids,MG)是集分布式发电(distributed generation,DG)、储能装置、变换器、负荷、监测和保护装置于一体的自主发电和配电系统,其既可以孤立运行,也可以并网运行[1-2].微电网具有可再生能源渗透率高、多能源互补、优化管理等特点[3-4].针对传统交流微电网中存在的谐波、环流和控制复杂等问题,文献[5]提出了一种H桥逆变器串联结构微电网.但该系统中还存在着相间功率平衡困难、微电源投切对系统运行性能影响较大等问题.

模块化多电平变流器(modular multilevel converter,MMC)具有子模块易于扩展、输出多电平电压、谐波含量低等优点[6].文献[7]利用这些特点,将风、光等微源与储能装置通过变换器并联在MMC每个子模块的电容两端,构建了一种基于MMC的半桥串联结构微电网(modular multilevel converter microgrids,MMC-MG).该系统具有微源控制灵活、输出功率等级高、冗余度好、相间功率易调度等优点.目前,针对MMC-MG系统的研究主要集中在其输出特性分析、输出电压稳定控制以及孤岛运行模式下微源功率的协调控制等方面[8-9].但关于MMC-MG系统并网的相关控制策略研究较少.

微电网并网控制的关键是其输出功率和电流都应快速、实时地跟踪其参考值[10].内环电流控制直接关系到并网逆变器的稳态精度、谐波含量、动态响应和抗干扰性能.并网电流控制技术主要包括矢量控制和直接功率控制[11].输出电流应与电网电压具有相同相位和频率的高质量正弦波,而且谐波含量要低,以减少对电网的影响.普通三相逆变器的并网电流控制方法包括滞环控制,PI控制,预测控制等[12-14].

MMC-MG结构中存在大量的电力电子器件.在理想情况下,采用脉宽调制技术,并由MMC逆变环节产生多电平电压.在实际情况下,为避免子模块中上、下功率开关器件同时导通,功率器件管压降,逆变环节的延迟等问题[15],MMC逆变环节将存在一定程度的非线性特性.传统非线性系统的控制主要有反馈线性化、逆系统等.但这些控制方法多数具有计算量大、控制复杂、鲁棒性差等缺点,会对系统的控制造成一定的影响[16].而基于无源理论的控制本质上是对非线性系统的能量进行控制,通过注入阻尼和重新分配系统的能量,使系统在满足无源性条件时达到较好的控制性能,这种方法从系统能量的角度出发进行控制器的设计,从而使非线性系统的控制器设计得到简化[17].目前,无源控制(passivity-based control,PBC)方法现已成功应用于高压直流输电、并网PWM变换器、光伏Z源逆变器、同步发电机混沌系统控制和基于MMC的超导储能(superconducting magnetic energy storage,SMES)系统的非线性控制中[18-22].

另外,MMC-MG系统在不同的环境条件下,含风、光等随机性微源的发电模块(generation module,GM)输出功率存在一定的波动.而且由于系统的非线性特性,若在该系统的并网电流控制中采用传统PI控制,不仅会导致系统的动态性能较差,而且电流谐波含量偏高.

因此,本文针对上述问题,将非线性无源控制理论引入到MMC半桥串联结构微电网的并网电流控制中.首先,介绍了MMC-MG并网系统的基本拓扑结构,并建立了系统的欧拉-拉格朗日(Euler-Lagrange,EL)数学模型;然后,结合能量存储函数与电流的期望平衡点,以得到无源控制律.并设计了无源电流控制器;最后,从动态性能、谐波特性方面对传统PI电流控制与本文所涉及无源电流控制器进行了对比分析.并通过仿真验证了该控制策略的正确性和有效性.

2 系统拓扑结构

MMC-MG并网拓扑结构如图1所示.该系统中,每相均以2N个发电模块(generation module,GM)为基本单元,采用MMC拓扑结构组成三相逆变环节,然后经过滤波器、静态开关等连接至外电网,本地交流负载群接至交流母线上.系统中每个桥臂由N个GM和一个电感L串联而成.

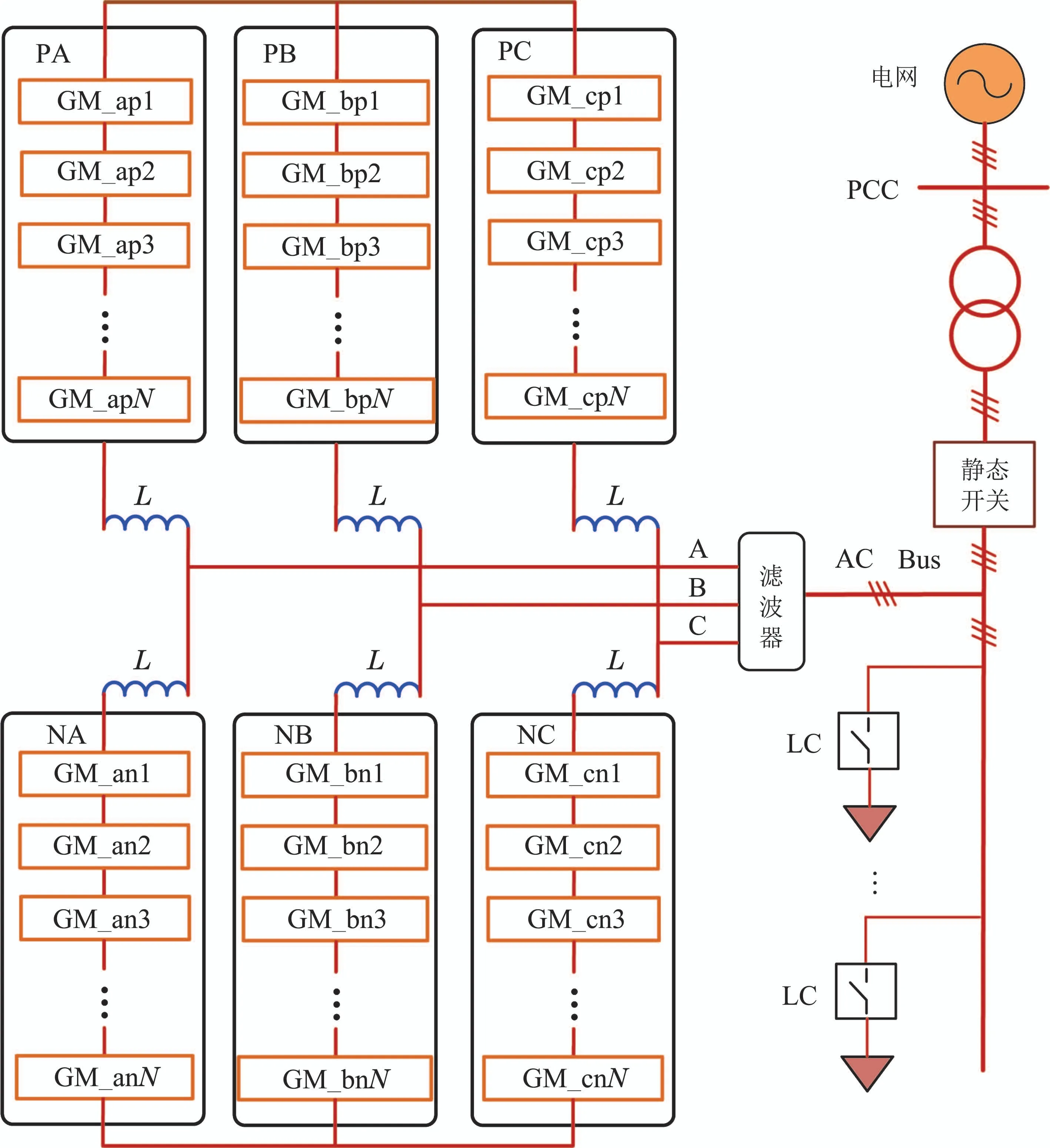
图1 MMC-MG并网拓扑结构Fig.1 Grid-connected topology of the MMC-MG

发电模块GM由风力(光伏)微源、AC/DC可控整流电路(DC/DC直流变换电路)、储能装置(energy storage devices,ESD)、半桥变流器(half-bridge converter,HC)组成.每个桥臂包含N个级联的发电模块(GM).如图2所示.

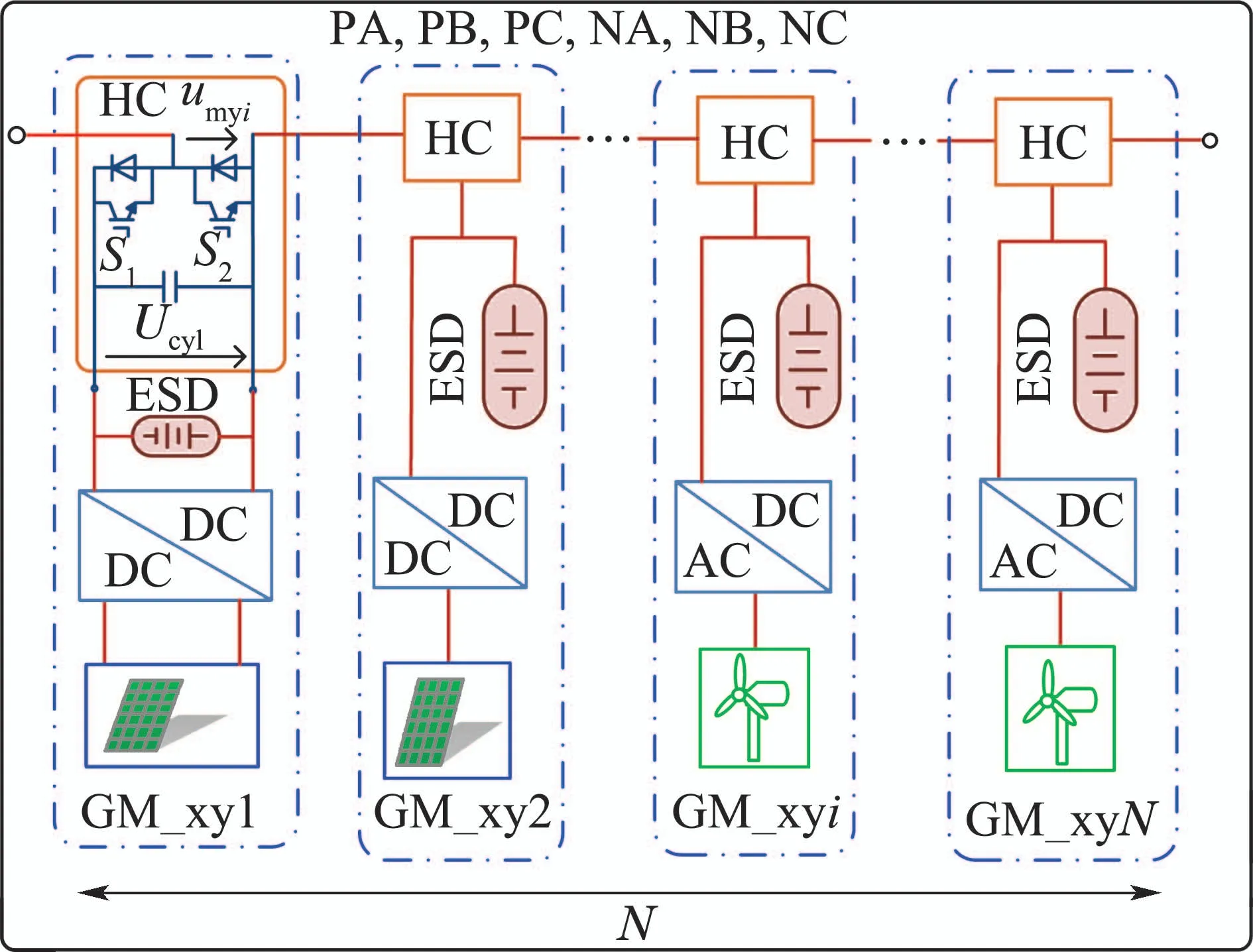
图2 桥臂拓扑结构Fig.2 Topology of each bridge arm

系统正常运行中,GM 有投入和切除两种状态.GM 处于投入状态(HC 中,S1=1(开通),S2=0(关断))时,其输出电压等于微源直流链电压,即umyi=Ucyi;GM处于切除状态(HC中,S1=0(关断),S2=1(开通))时,其输出端电压等于零,即umyi=0.因此,可以用开关函数Kxyi表示GM的投切状态,则在一个工作周期内:

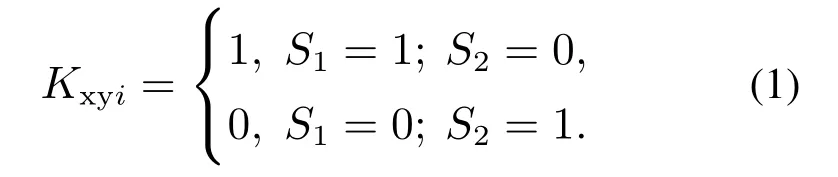
3 MMC–MG的EL模型

系统中,每相投入的N个GM输出电压叠加,可获得系统多电平输出电压.将各GM等效为受控电压源,则MMC-MG简化的等效电路如图3所示.

图中,Ls,Rs为滤波电感和线路等效阻抗;L,R为桥臂电感和等效电阻;i1x表示三相输出电流;iex为电网侧电流;iLx为三相负载电流;esx表示三相电网电压;ixy为上、下桥臂电流;uxy为桥臂中N个GM输出电压之和;uxo表示系统输出电压;VPN为直流侧虚拟母线电压.其中,x=a,b,c;y=p,n.

根据图3所示的等效电路,以A相为例,上、下桥臂中N个发电模块GM的输出端串联连接,其输出电压之和为

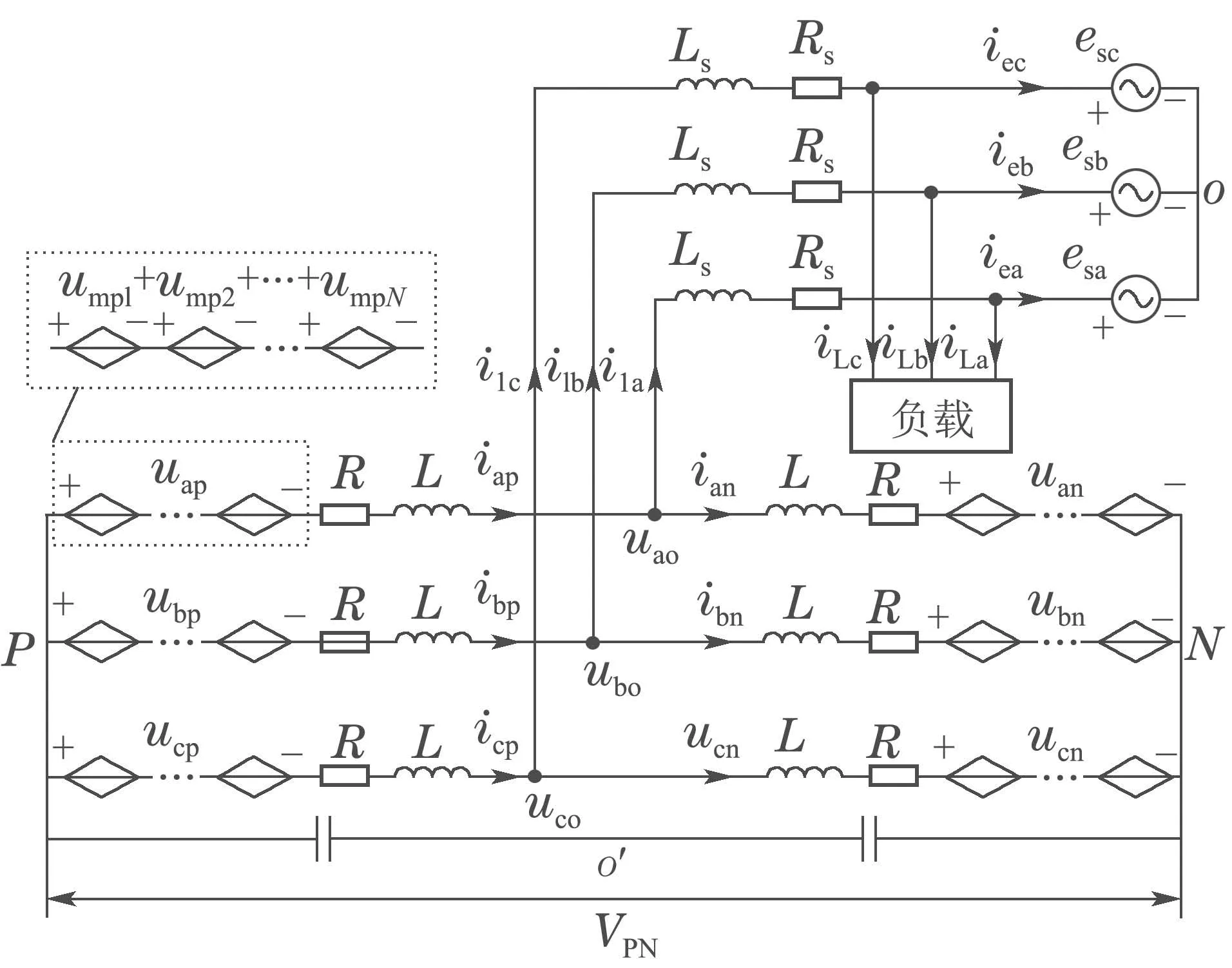
图3 MMC-MG简化的等效电路Fig.3 Simplified equivalent circuit of the system

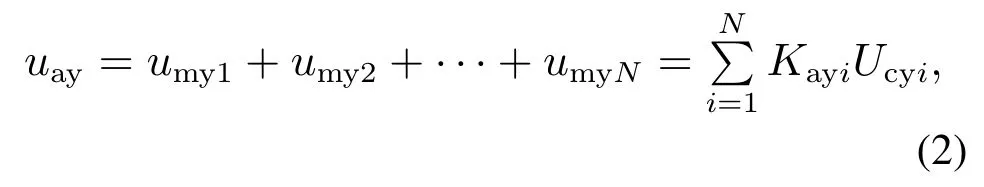
式中:Kayi为桥臂中GM的开关函数;Ucyi为微源直流链电压.在三相电网电压平衡的情况下,由基尔霍夫电压、电流定律可得

系统等效输出电压可以表示为

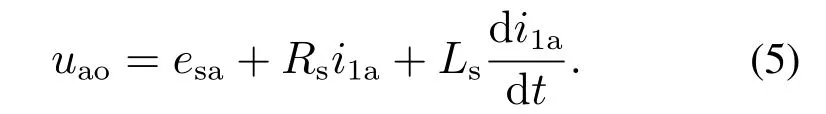
由式(3)可得

由式(5)-(6)可得到A相交流输出侧数学模型

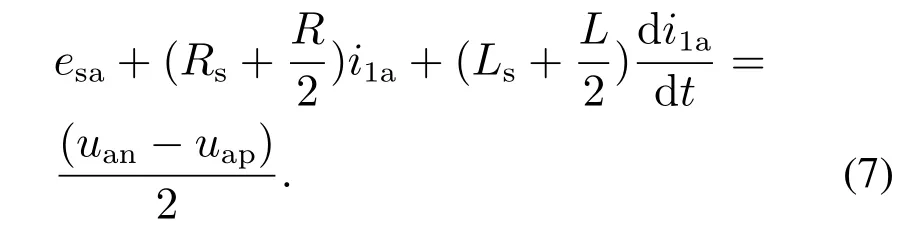
同理,可得B,C相数学模型

然后,对式(9)进行变换,可得到dq旋转坐标系下的数学模型

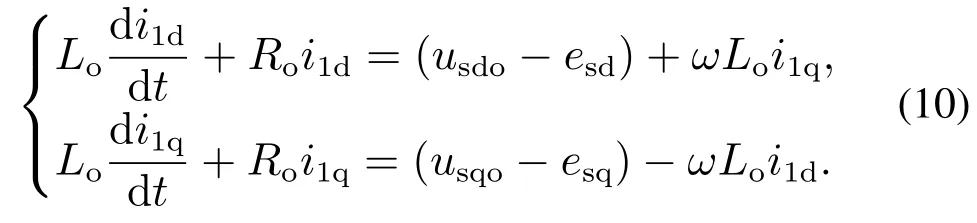
式(10)也可以写成如下形式:

4 MMC–MG无源电流控制器设计

在多输入多输出系统中:若存在正定函数L(x),对任意的T ＞0,得到以下耗散不等式[16]:

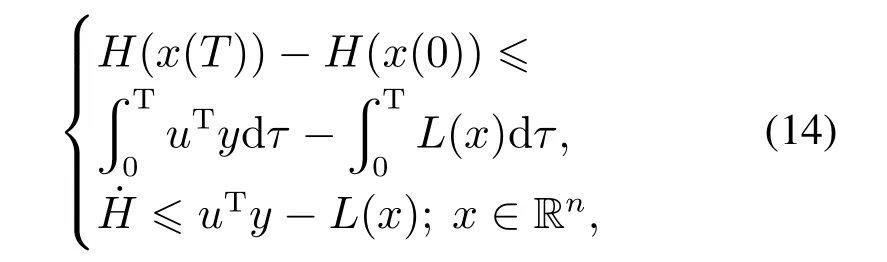
其中H(x)为其能量存储函数.对于系统的输入u、输出y及能量供给率uTy成立,则该系统具有严格无源性.由此可知,式(14)为严格无源不等式.

针对式(13)所示MMC-MG并网系统的模型,设其存储能量函数为

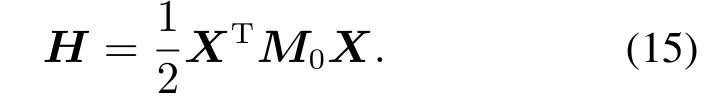
能量函数的导数与式(13)相结合可得到

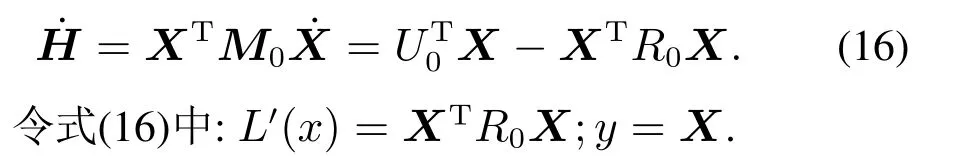
通过对比式(16)与式(14),得知两者有相同的形式,故该系统是严格无源的.

设状态变量的期望平衡点为

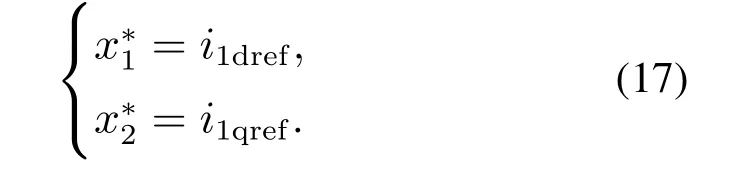
则状态变量的误差为

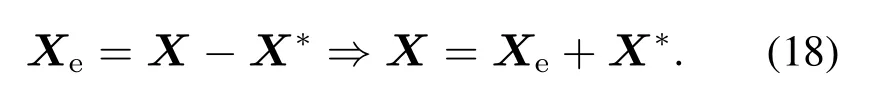
将式(18)代入式(13)的动态矩阵方程,有

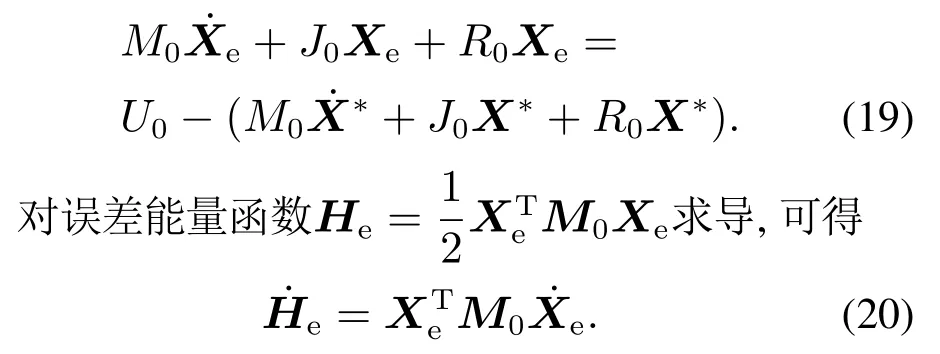
将式(19)代入式(20)有

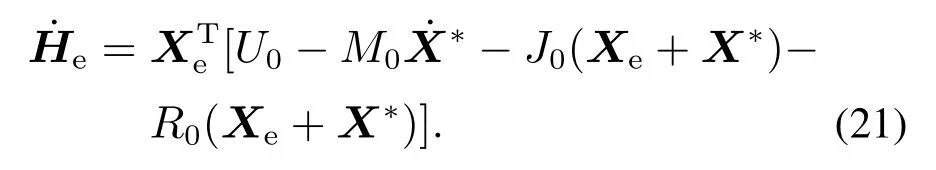
为使系统的状态变量快速恢复至其期望的平衡点,须使误差能量函数快速收敛至零.因此,需设置阻尼项使能量快速耗散.设增加的阻尼耗散项为R1Xe,则系统内部耗散项变为

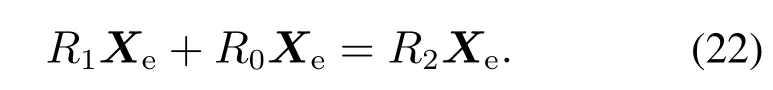
将式(22)代入式(19),有

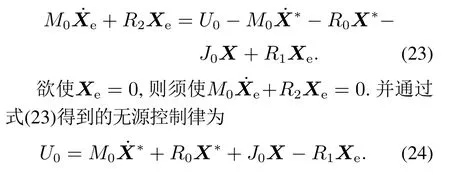
为了对该电流控制器的性能进行分析,将式(11)和式(25)相结合,得到电流与其参考值之间的关系:

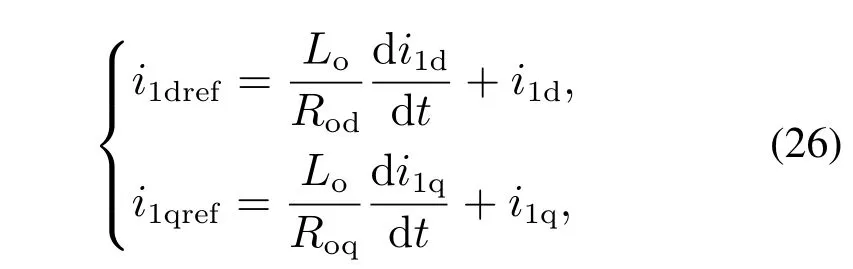
式中:Rod=Ro1+R11;Roq=Ro2+R12.

从式(26)可知,若选择合适的阻尼值Rod,Roq,则i1d,i1q很快稳定于其参考值i1dref,i1qref.误差能量函数收敛至零的速度由所设置阻尼值Rod,Roq的大小决定.为分析该无源电流控制方法的性能,设置不同阻尼值时所对应的幅频、相频特性曲线如图4所示.图中,无源特性曲线从左至右阻尼值逐渐增大,谐振峰值也随之增大,快速性增强,但所对应稳定裕度γ相应减小,稳定性也随之降低.与PI控制特性曲线相比,无源控制(PBC)特性曲线快速性较好.

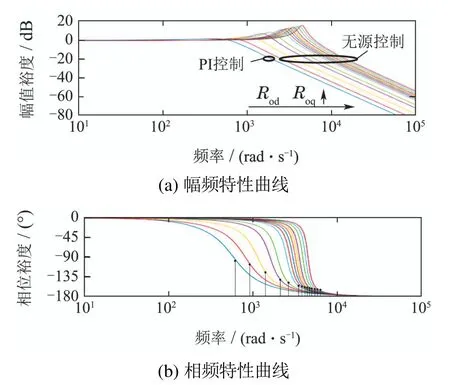
图4 设置不同阻尼值时幅频、相频特性曲线Fig.4 Amplitude-frequency and phase-frequency characteristic curves with different damping values

因此,通过式(25)可以得到本文所设计的无源电流控制器:

为同时兼顾系统快速性和稳定性,需要合理选择阻尼值.通过计算与多次仿真试验,采用无源电流控制算法时阻尼值与其对应的稳定裕度γ,如图5(a)所示.从图中得知,适用于MMC-MG并网系统的阻尼值在30～130之间.调整该参数时还需兼顾系统输出电流的谐波含量.通过仿真,并对比不同参数时电流的谐波畸变率,发现稍大的阻尼值可以获得较好的谐波特性,如图5(b)所示.故本文选择Rod,Roq=48.

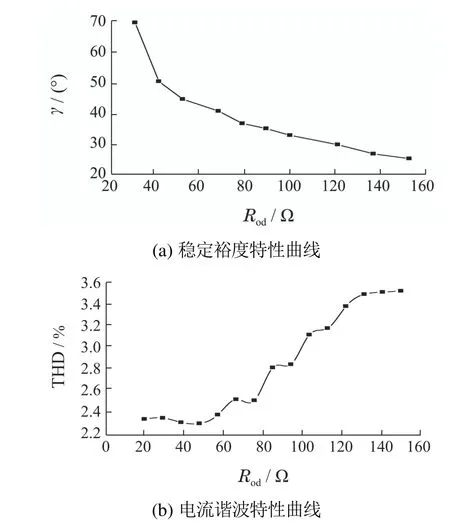
图5 阻尼值与稳定裕度、谐波特性关系曲线Fig.5 The curve between damping value,stability margin and harmonic characteristics

图6给出了采用两种控制方法时系统A相输出电流的频谱分析.采用无源控制时,其谐波畸变率THD1=2.33%,如图6(a)所示;若采用PI控制,电流谐波畸变率THD2=2.59%,如图6(b)所示.由此得知,相比于PI控制,采用无源电流控制时输出电流谐波畸变率降低了0.23%,谐波特性较好.

图6 A相输出电流频谱分析Fig.6 Spectrum analysis of phase A output current

以上分析了系统并网运行时内环电流的无源控制特性.由式(17)所示的状态平衡方程中,电流参考值i1dref,i1qref由功率外环控制得到.外环功率控制仍采用传统的PI控制器.因此,输出电流的平衡点为

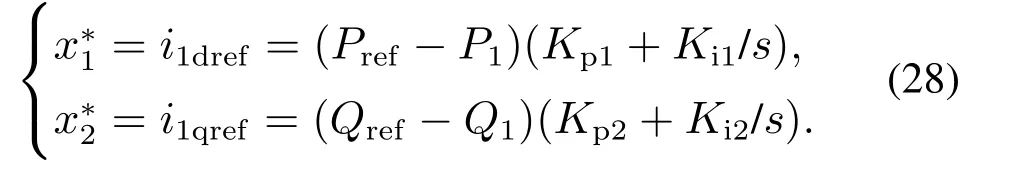
结合式(28)可知,微电网输出有功功率P1与其参考值Pref相比较后,通过PI控制器即可得到i1dref;同理可得到i1qref,如图7所示.

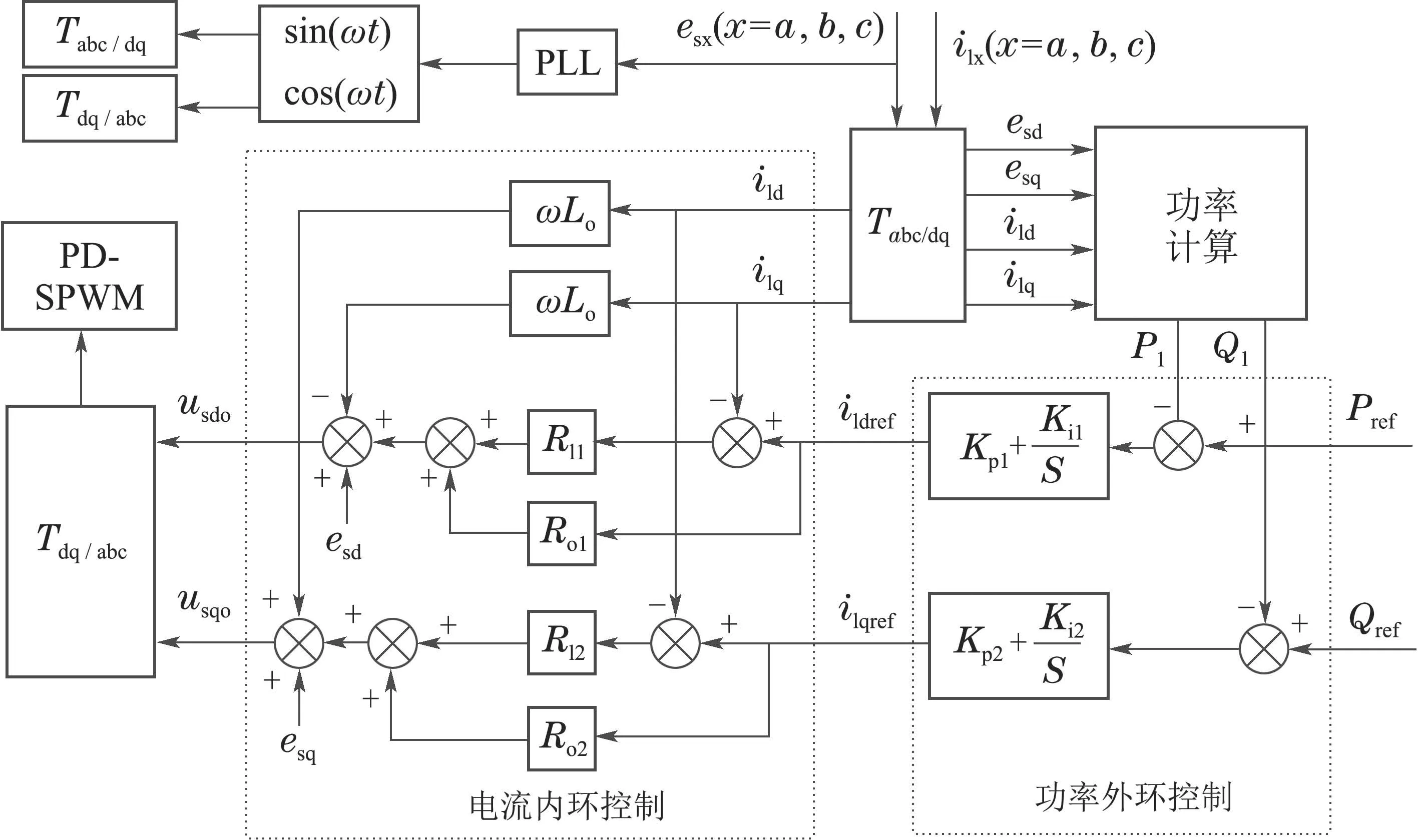
图7 系统输出功率、电流控制框图Fig.7 System output power and current control block diagram

通过以上分析,MMC-MG系统并网双闭环控制框图如图8所示.由图得知,系统的总体控制中,首先通过输出功率期望值、实际输出功率及式(28),可得到输出电流各分量的期望值i1dref,i1qref.然后,由无源电流控制器及Park变换得到三相输出电压参考值uxref;并通过载波层叠调制(phase disposition PWM,PD-PWM)算法得到各GM的开关驱动信号.

图8 系统并网控制框图Fig.8 Control block diagram for the system

根据能量守恒定律,微电网输出功率P1是传输至网侧功率Pe和负载消耗功率PL之和,三者之间的关系应为:P1=Pe+PL.系统输出电压由于电网电压的牵制作用而保持不变,故其输出电流之间的关系为

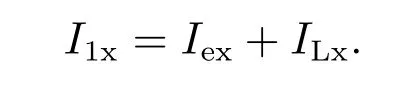
5 仿真分析

为验证本文所述无源电流控制的有效性,搭建了MMC-MG系统的并网仿真模型.系统仿真参数与微源参数如表1-2所示.

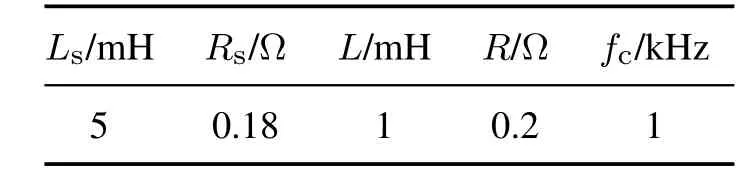
表1 系统仿真参数(N=4)Table 1 System simulation parameters(N=4)

设定环境温度为25°C,光照强度为1000 W/m2,平均风速为7.6 m/s.当光照、风速等条件未发生变化时,由于GM直流链上储能的存在,计及线路电压损耗,使微源直流链电压幅值稳定在160 V.每相上、下桥臂中GM输出端串联.因此,通过投入的N个GM输出电压串联叠加,以满足系统输出311 V相电压的要求.系统达到稳定时,在0.8～0.84 s内,系统输出线电压和相电压波形,如图9所示.

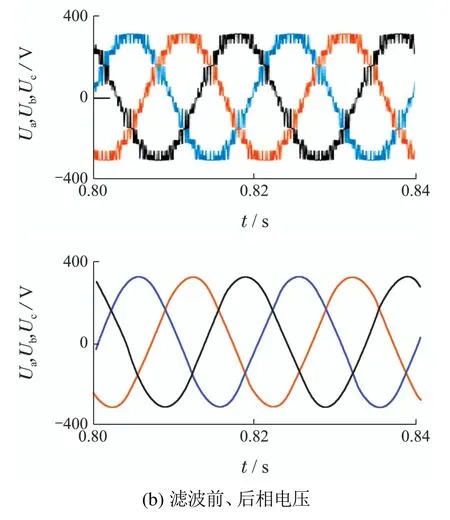
图9 系统输出电压波形Fig.9 Output voltage waveform of the considered system

在0.4～0.48 s内,A相并网点电压和电流的波形,如图10(a)所示.电压幅值为311 V,基波角频率为314 rad/s,电压、电流的相位差为0.而且,系统进行单位功率因数运行,如图10(b)所示,功率因数PF=0.99.

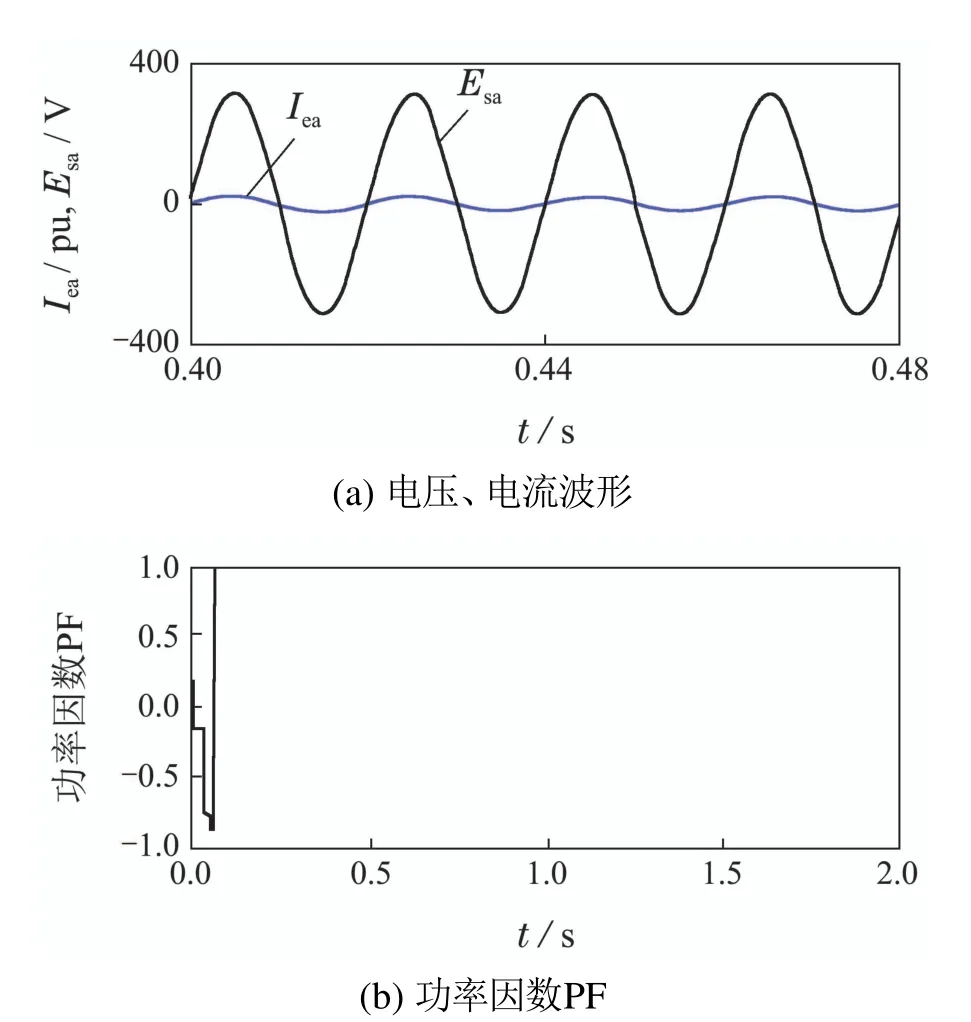
图10 电网电压、电流及功率因数波形Fig.10 Voltage,current,and power factor

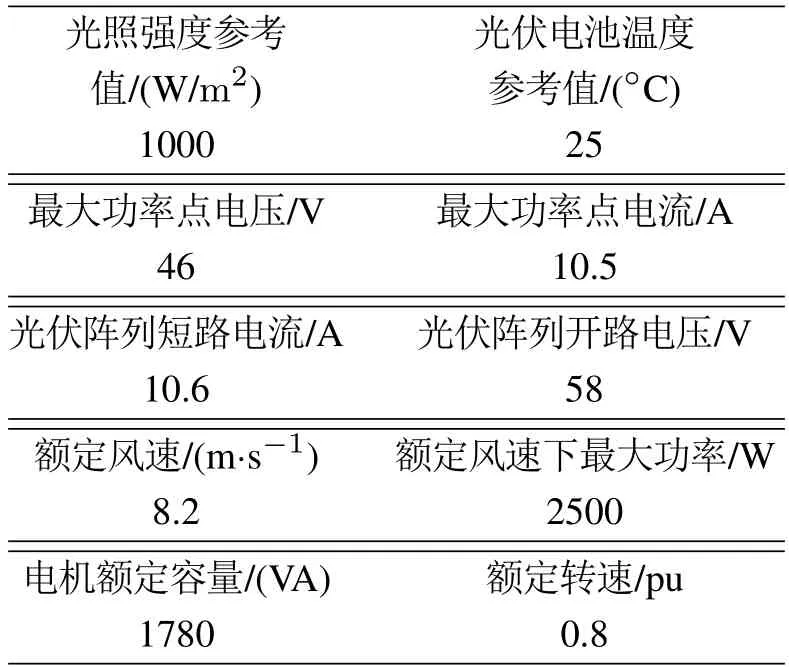
表2 微源仿真参数Table 2 Microsource simulation parameters

5.1 输出电流指令值突变

输出电流参考值通过功率外环得到,故在系统稳定运行后,输出功率指令值与负载功率值设置如下: 在1～1.5 s内,Pref=1.0 pu;在1.5～2 s内,Pref=1.5 pu(基准值为0.3 MW);在1～2 s内,Qref=0 pu(基准值为0 MVar),PL=0 pu.如图11所示,在1.5 s前,P1=Pe=Pref=1.0 pu.在1.5 s时,Pref升高.在1.5 s后,P1=Pe=Pref=1.5 pu.

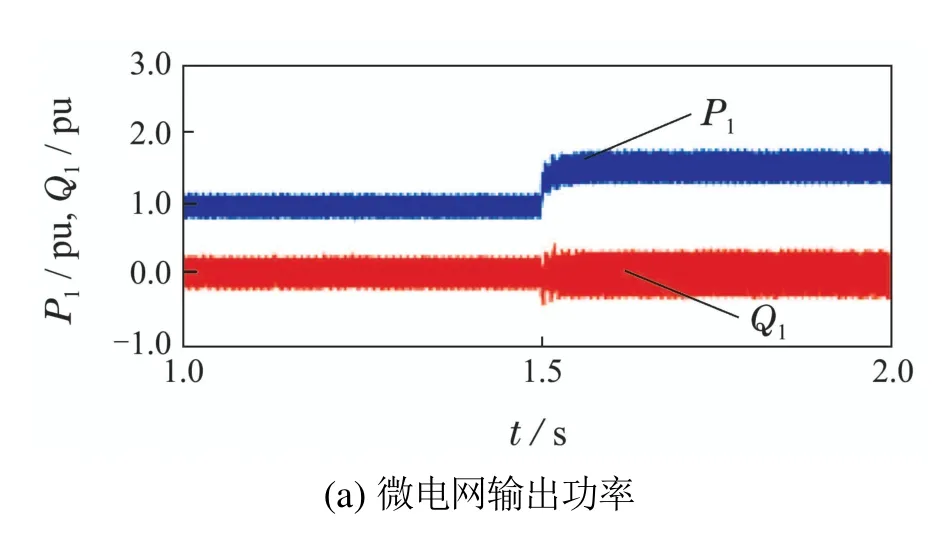
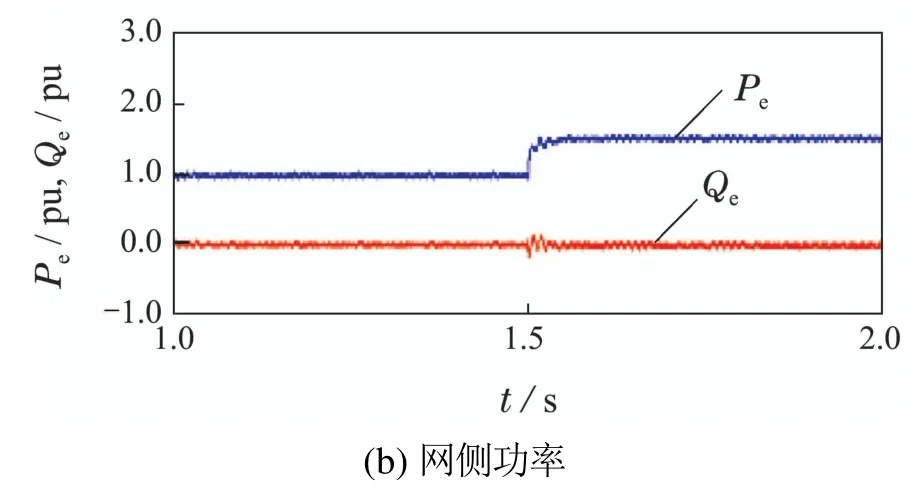
图11 输出功率波形图Fig.11 Output power waveform of the system

同时,在1.5 s时,输出电流(基准电流值0.6 kA)由于功率的突变而增加,并经过短暂调节后实现无静差地跟踪其参考值,如图12(a)所示.系统频率f在1.5 s发生短暂波动后恢复正常,且保持在±2%的误差要求之内,不影响系统的稳定运行,如图12(b)所示.

图12 系统输出电流、频率Fig.12 Output current and system frequency of the system

为进一步说明无源电流控制方法的有效性.图13给出了电流环中使用无源控制和传统PI控制时,输出电流的d轴分量和输出功率波形.从波形可以看出,与PI控制算法相比,采用非线性无源控制时系统的动态性能有较大的提高.

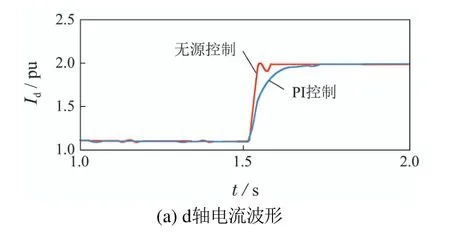
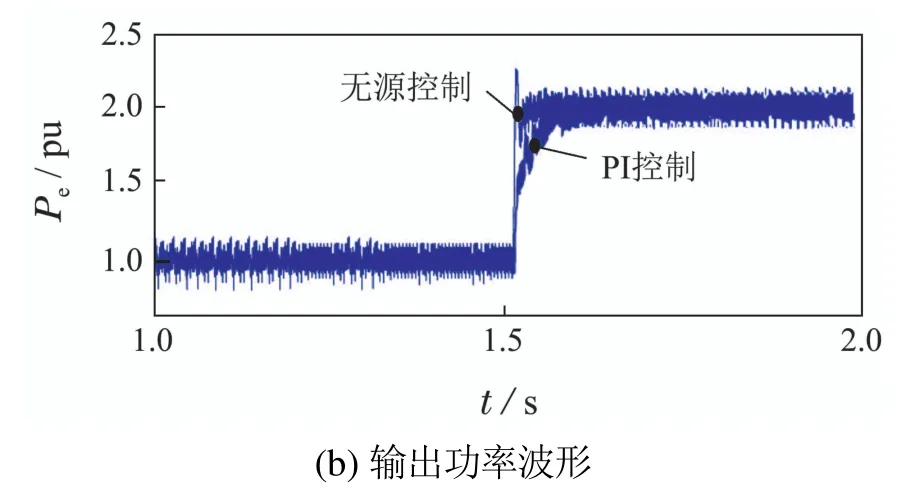
图13 两种控制方法的动态性能对比分析Fig.13 Dynamic performances of the two control methods

5.2 微源功率突变

考虑到微源输出功率具有随机性的特点,若某微源输出功率在2 s时发生突变,如图14所示,输出电流随输出功率的轻微升高而产生波动,但在短时间内恢复正常.输出电压保持不变,系统频率波动非常小,但均保持在规定允许的范围内,其波形与12(b)类似.

图14 系统输出电流、功率波形Fig.14 Output current and power waveform from the system

5.3 负载功率突变

针对负载功率突变的情况,设Pref=1.0 pu,Qref=0 pu,在系统交流母线上通过断路器接有功功率PL=0.3 pu的负载.通过控制断路器,使负载在2.5 s时退出系统,5 s时接入系统,7 s时又退出系统.

输出功率变化如图15所示,在2.5 s时,由于负载功率PL从0 pu突增至0.3 pu,传输至电网侧的功率Pe从1.0 pu突降至0.7 pu;同理,负载功率在5 s突降、7 s突增时,网侧功率Pe确随之增加、降低;但总输出功率保持不变,即:P1=Pref=Pe+PL,满足能量平衡关系.

图15 输出功率变化波形图Fig.15 Output power variation waveform

如图16所示,由于电压保持恒定,网侧电流Iex和负载电流ILx大小随其功率的变化而变化,但其总输出电流I1x不变,即:I1x=I1ref=Iex+ILx.

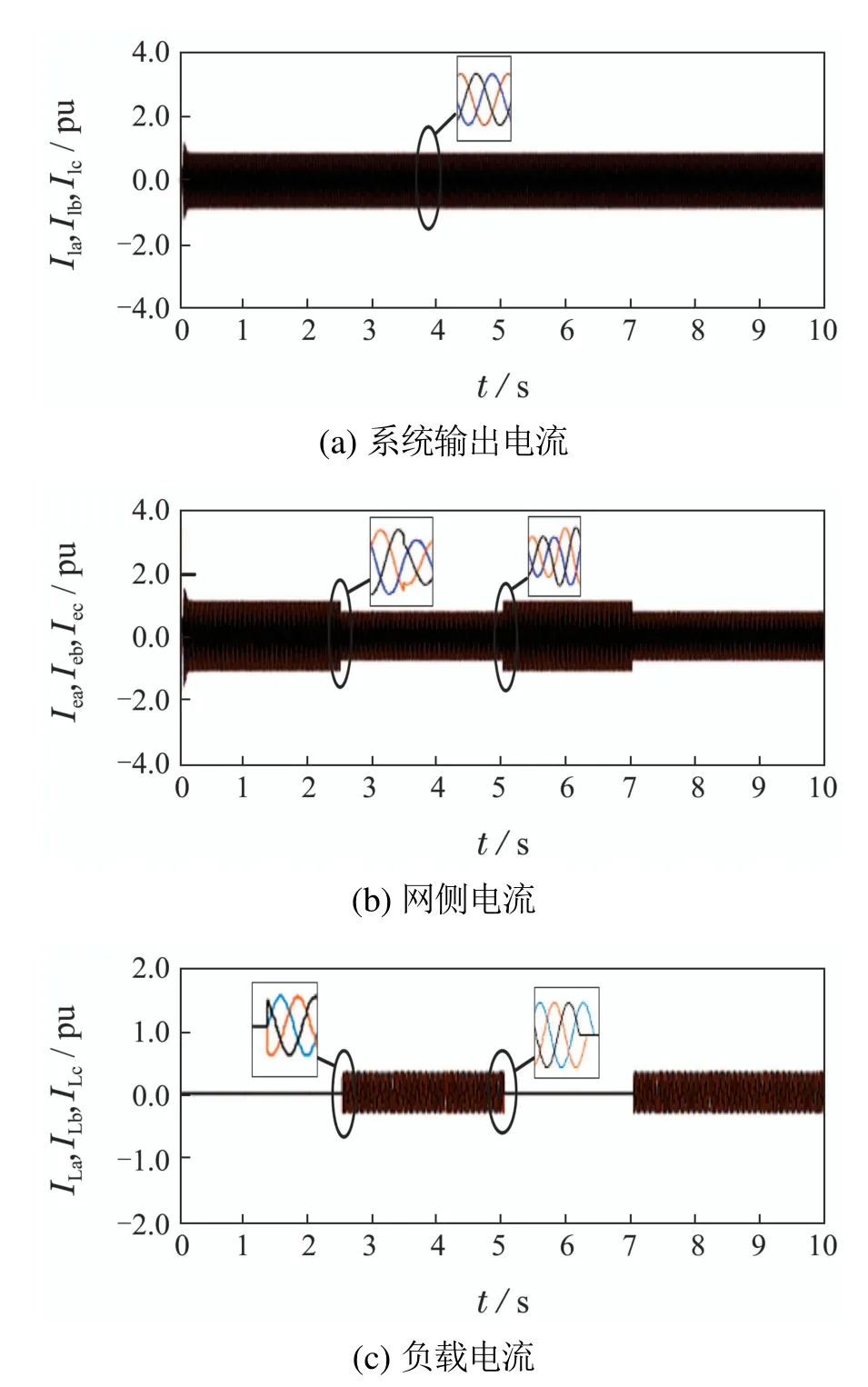
图16 输出电流变化波形图Fig.16 Output current variation waveform

如图17所示,负载在2.5 s,5 s,7 s发生突变时,系统频率f发生微小波动,仍满足±2%的误差要求之内,不会对系统的正常运行产生影响.

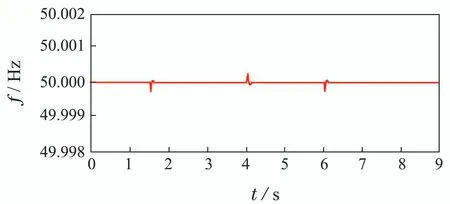
图17 系统频率f变化波形图Fig.17 System frequency f variation waveform

以上分析可知,系统正常运行中负载功率发生突变时,系统输出功率、电流均能快速且实时地跟踪其指令值.采用该无源电流控制方法可有效保证系统运行的稳定性.

6 结论

基于MMC-MG并网系统的EL模型及其无源性,结合注入阻尼参数与期望状态平衡点得到无源电流控制律;并根据该控制律设计了无源电流控制器,使系统快速收敛于稳定状态.仿真结果表明,与传统PI控制相比,阻尼注入的无源电流控制方法能获得更好的动态特性.另外,该控制方法在系统运行于输出电流指令值、负载功率、微源功率突变等不同工况时均能实现对功率、电流的快速跟踪.同时,输出电流的谐波含量较低.该阻尼注入无源电流控制方法可作为进一步研究系统相内微源功率分配、相间功率平衡等特性的有利工具.