无速率编码中度分布的研究和发展

2022-11-07乔越伏玉笋原牧云唐金辉

电信科学 2022年10期

乔越，伏玉笋，原牧云，唐金辉

综述

无速率编码中度分布的研究和发展

乔越1,2，伏玉笋2,3,4，原牧云1,2，唐金辉2

（1. 上海交通大学宁波人工智能研究院，浙江宁波 315000；2. 上海交通大学电子信息与电气工程学院，上海 200240；3. 系统控制与信息处理教育部重点实验室，上海 200240；4. 上海工业智能管控工程技术研究中心，上海 200240）

无速率编码作为一种纠删码，在减少反馈重传的同时也具有码率灵活、编译码简单的特性，在许多领域都有广阔的应用前景。度分布作为无速率编码设计的基础，对无速率编码的性能有至关重要的影响。随着无速率编码的广泛应用，度分布的设计也需要随着场景和需求的变化进行优化。首先论述了无速率编码的发展与应用，从几种经典的无速率编码和度分布开始，详细地从应用场景、优化目标以及现有优化方法3个角度，对目前无速率编码中度分布的研究和发展进行了总结与分析。最后，对无速率编码和度分布的发展应用趋势进行了分析与展望。

无速率编码；喷泉码；度分布；网络编码；多路径

0 引言

随着网络的发展，人与人、人与物、物与物之间的连接越来越紧密，随之而来的就是海量的信息传输，这对通信技术提出了更高的要求，同时推动了通信技术的快速发展。

在网络数据传输中，传输控制协议是常见的用来保证信息可靠传输的通信协议，在正确接收到每个包后，接收端会通过反馈信道向发送端发送确认信息。如果发送端接收到重传的请求，或者发送端并未接收到确认信息，就需要重新发送这个数据包，直到接收到确认信息。这种传输机制固然会使信息的传输变得可靠，但同时也会带来一些弊端，例如，当发送端和接收端距离较远时，发送端需要长时间接收来自接收端的反馈信息，在此期间发送端不能再进行发送，导致较大的传输时延。同时，当信道情况较差时，接收端很难正确接收信息，会不断请求发送端重传信息，形成“反馈风暴”，导致大量的资源浪费在反馈和重传上。

为了应对这一问题，一种不需要反馈重传的编码技术应运而生，即纠删码技术。在纠删码中，发送端先对原始信息进行编码，在信道传输中可能会丢失部分的码字，但是在接收端仍然可以根据接收到的部分码字恢复全部信息。这样就在没有反馈重传的情况下实现了可靠传输，避免了“反馈风暴”的产生，但是这种纠删码仍然存在不足之处，比如在信道状态不断变化的情况下，固定的编码速率难以保持良好的通信，同时编译码速度慢，导致时延增加。因此，一种无速率的、编译码简单的纠删码技术——无速率编码，产生了。

无速率编码也叫数字喷泉码，采用数字喷泉编码的网络，发送端将信息像喷泉一样源源不断地发出，数字喷泉码示意图如图1所示，水滴就是发送出去的编码符号，接收端则像一个在喷泉下接水的杯子，只要杯子装满了水，不管装的是哪些水滴，都代表接收到足够的编码符号来译码出原始信息。这正是数字喷泉码名称的由来。数字喷泉编码具有无码率的特性，可以按照某个概率分布产生任意数量的码字，因此可以通过自适应信道状态来改变码率，而这个概率分布就是本文重点研究的度分布。

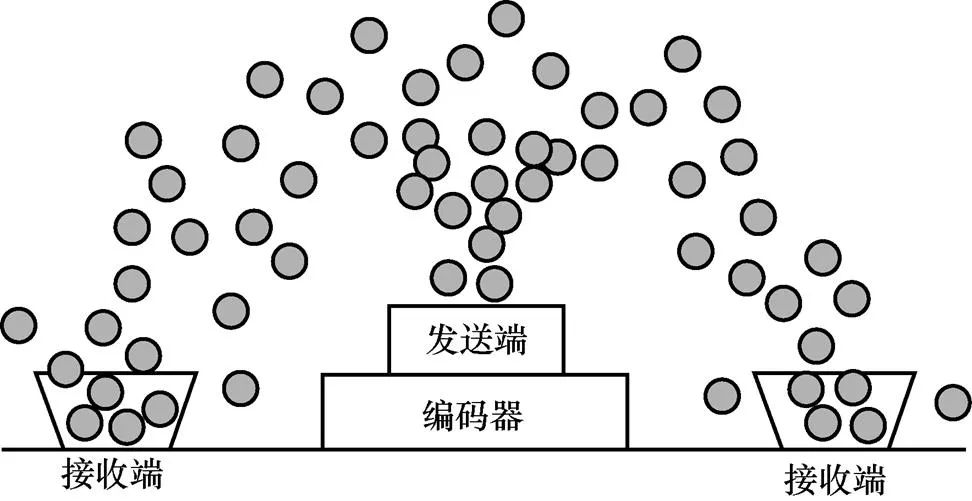
图1 数字喷泉码示意图

无速率编码自提出以来就受到了广泛的关注。自2002年Luby[1]提出第一种可以实际使用的无速率编码——卢比变换（Luby transform，LT）码以来，多种无速率编码在此基础上被提出，主要有Raptor码[2]、模拟喷泉码[3]、分批稀疏（batched sparse，BATS）码[4]以及在线喷泉码（online fountain code，OFC）[5]等。它们或是在编码结构上加以组合扩展，或是在编码方法上进行改造，从而提升无速率编码的译码成功率。无速率编码由于具有复杂度低、码率灵活等特性，拥有十分广泛的应用场景，比如存储、广播通信和无线传感器等。目前，无速率编码已经被写入第三代合作伙伴计划（3rd Generation Partnership Project，3GPP）、手持数字视频广播（digital video broadcasting-handheld，DVB-H）等国际标准，同时也正在参与其他多项国际标准的制定，拥有广阔的应用前景。度分布的设计是无速率编码中非常重要的一环，度分布的好坏直接影响喷泉码的性能。一个优秀的度分布需要能在尽可能少地接收编码符号的同时保证较高的译码成功率，而且保持较低的编译码复杂度。随着无速率编码的应用逐渐广泛，度分布也有了各种发展，比如不同应用场景下的度分布、不同优化目标的度分布等。尽管目前已经有一些关于数字喷泉码和度分布的综述性论文[6-8]，但是这些论文中都缺少对度分布全面详细的介绍，比如联合度分布和针对码长问题的度分布，也缺少对度分布的研究整合，比如对度分布的优化目标的总结。因此本文希望能够从多个角度对度分布的研究进行分析总结，从而为无速率编码度分布的设计和优化提供参考。

1 无速率编码发展与应用总结

如前所述，无速率编码也被称作数字喷泉码，能够不受固定码长的限制，产生任意多的编码符号[9]。同时它只需接收一定数量的编码符号就可以完成译码，对符号的接收顺序并没有要求。

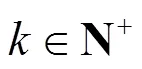
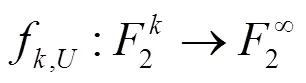
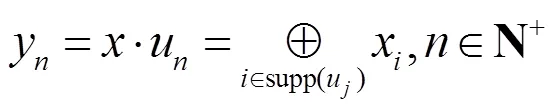
输入符号和输出符号之间的关系可以用二分图表示[11]，这种用二分图表示输入输出符号之间关系的方法由Tanner提出，因此也叫Tanner图，此处不再对Tanner图展开介绍。

目前的无速率编码主要有LT码、Raptor码、模拟喷泉码、BATS码、OFC等。下面对这些无速率编码的特点和优势进行简单的介绍。

（1）LT码

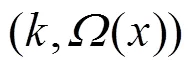
（2）Raptor码

LT码的编译码方法复杂度较低，但其复杂度并非线性的，而且存在“错误平底”现象[10]，因此有人提出一种新的无速率编码——Raptor码[2]。复杂度是指完成编码或者完成译码所需要的符号操作数，Raptor码的编译码复杂度均与源符号数呈线性关系，低于LT码的复杂度。Raptor码是对LT码的直接改进，首先通过低密度奇偶校验（low density parity check，LDPC）码对信源符号进行预编码，生成中间符号，再对中间符号用LT码进行编码，得到编码符号。在译码时，首先对LT码进行译码，再对恢复出的中间符号进行LDPC码译码，即便在LT码译码时丢失少量中间符号，还是有大概率可以在之后的LDPC码译码中恢复出所有的信源符号。目前最新的Raptor码——RaptorQ码的国际标准于2011年8月发布的RFC6330标准中阐述。

（3）模拟喷泉码

模拟喷泉码最早由Shirvanimoghaddam等[3]在2013年提出，它为各个变量节点分配权重，最终使编码分布能够服从高斯分布，以此适用于无线信道的传输，它被证明在无线信道下能够具有接近信道容量的性能。在编码过程中，首先要对数据包进行二进制相移键控调制，再通过度分布函数采样得到度数，之后选取个信息符号和权重系数，组合得到编码符号。在译码方面，采用压缩感知置信传播译码算法，与BP译码不同的是，BP译码在变量节点和校验节点之间传递信息，而压缩感知置信传播译码在变量节点和约束节点之间传递信息。

（4）BATS码

BATS码是Yang等[4]在2014年提出的一种将喷泉码和随机网络编码结合的新型无速率编码，它在具有喷泉码无速率、低编译码复杂度等特性的同时，还拥有网络编码的吞吐量增益。BATS码的所有操作均为线性操作，因此它对丢包网络以及动态网络拓扑具有很好的鲁棒性。

BATS码在编码时，其度分布以及编码参数会根据传输文件大小、信道状况等信息来选择，首先对信源符号进行LT码编码，生成不同批次的编码包，之后在中间节点对同一批次的编码包进行随机网络编码，生成BATS码。在接收端接收了足够数量的编码包之后，就可以进行译码，目前BATS码常用的译码算法包括置信度传播译码算法、高斯消元译码算法以及基于这两者的一些改进算法。

（5）OFC

OFC[5]是一种新型无速率编码，本质上是一种利用了反馈信息的LT码，但是OFC可监控性更高。OFC的发送端可以根据接收端反馈得到的实时译码状态寻找最优的编码策略，是一种具有实时性的编码，而且相比其他实时性编码，OFC具有更小的译码开销。

OFC的编译码方法和LT码类似，但OFC在译码时只接收两种情况的编码符号：只包含一个接收端未知信源符号的编码符号和只包含两个接收端未知信源符号的编码符号。其他编码符号则会被直接丢弃。

最初无速率编码的设计目标为在广播和数据分发场景下的应用。而无速率编码的编译码复杂度较低，而且码率灵活，因此其在水中通信、汽车通信、存储和计算、无线传感器网络等应用中也有很大的潜力。无速率编码技术以及应用场景见表1。

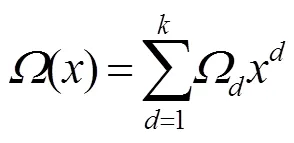
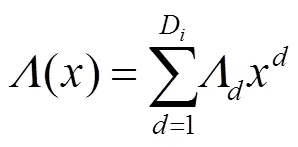
表1 无速率编码技术以及应用场景

度分布在喷泉码中用于指导编码器按要求生成编码信息。找到一个合适的度分布是设计喷泉码的基础，喷泉码的效果在很大程度上是由度分布决定的。

2 经典度分布

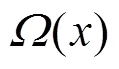
（3）重复以上步骤，直到完成译码。

2.1 理想孤波分布

ISD是一种理想状态下的度分布，分布函数为：

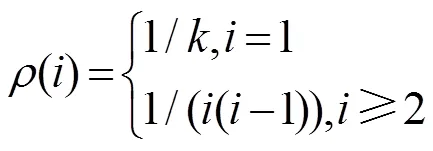
一般将已经确定而未处理的输入符号的集合称为可译集，那么在某一时刻这些输入符号的数量就是可译集的大小。随着译码过程的进行，度为1的输出符号被释放，越来越多的输入符号被确定，此时可译集的大小就会增加；而随着输入符号的处理，可译集又开始减小，但同时可能会产生下一个能够被释放的输出符号，由此生成循环。

2.2 鲁棒孤波分布

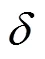
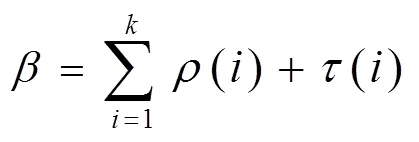
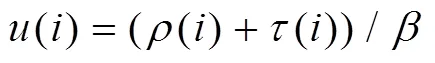
除了ISD和RSD，还有多种经典度分布函数，比如二进制指数分布（binary exponential distribution，BED）[31]、泊松分布（Poisson distribution，PD）等，许多研究都在此基础上展开，此处不针对这些经典度分布进行详细说明，后面会对基于经典度分布的改进进行介绍。

参考以上ISD和RSD的设计理念，可以看出度分布对无速率编码的影响主要在于编译码的复杂度以及译码成功率，二者都是常用的度分布评价指标。首先，当高度值的编码符号较多时，只需要较少的编码符号即可覆盖所有输入符号，但是由于缺少低度值的编码符号，BP译码很难顺利进行，因此BP译码成功率降低，而使用GE方法进行译码又会增加译码的复杂度；当低度值的编码符号较多时，固然译码成功率会提高，但是需要更多的编码符号来覆盖输入符号，导致编码复杂度较高。对喷泉码的期望是更低的编译码复杂度、更高的译码成功率。而这些期望反映在可译集上，即希望可译集尽量小，但是又能以较高的概率使可译集的大小大于或等于1。对应到ISD和RSD上，ISD有着较低的编译码复杂度，而在实际应用中的译码成功率却不够高，RSD针对可译集大小进行了优化，在略微提升复杂度的同时提高了译码成功率。后续的度分布优化研究同样大多致力于降低复杂度，或者提升译码成功率。

3 度分布设计与优化

3.1 不同场景下的度分布

自第一个无速率编码——LT码以及RSD产生之后，由于其复杂度低、码率灵活等特性，无速率编码受到了越来越多的研究和关注。而随着无速率编码广泛应用于多种不同的场景，度分布的设计也由于不同场景下信道模型的差异性而发生变化，常见的有删除信道、无线信道、分布式场景等。本节会介绍不同场景下度分布的设计与优化方案。

3.1.1 删除信道下的度分布

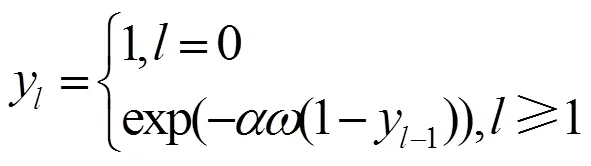
式（8）被称为删除信道下LT码的密度演化方程，通常被用来对LT码进行理论分析，也是无速率编码度分布设计与优化的重要工具。

根据式（8），Sejdinovic等[32]给出了删除信道下LT码的两种等价的度分布线性优化方案。这两种优化方案分别以最小复杂度和最小开销为优化目标。Zeng等[33]研究了严重删除信道下的度分布设计问题，并且提出了一种以最大平均恢复概率为目标的度分布优化方法。Tsai等[34]提出了新的密度演化方程来分析LT码的渐进性能，并进行度分布优化设计。

系统形式的码字通常比非系统形式的码字有更优异的性能，而现有针对系统码的无速率编码度分布优化工作比较少。Nguyen等[35]提出了系统LT（systematic Luby transform，SLT）码，并给出了一种能够在SLT码中提供与RSD相近性能的截短度分布。同样利用与或树分析，可以推出SLT码在删除信道下的渐进性能递推式。

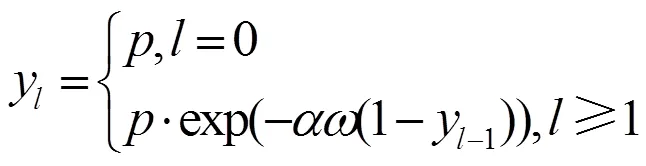
3.1.2 无线信道下的度分布

最初的喷泉码是针对删除信道提出的，但是随着对喷泉码研究的深入，发现在噪声信道中的喷泉码仍然有很好的性能，这里的噪声信道包括加性白高斯噪声（additive white Gaussian noise，AWGN）信道以及衰落信道。因此喷泉码也开始被应用于无线信道中。在研究无线信道下的喷泉码密度演化时，也可以采用类似LDPC码的方法，但是一般会较为复杂，因此大多采用简化后的方法，比如高斯近似方法。

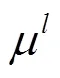
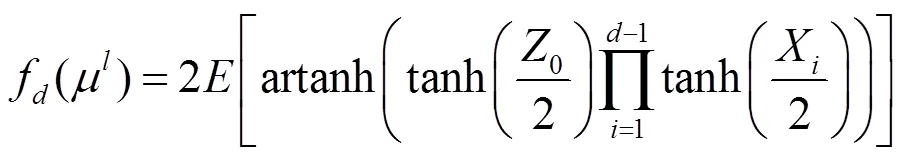
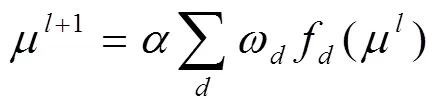
Etasami等[10]利用式（10）和式（11）提出噪声信道下喷泉码的度分布优化模型。

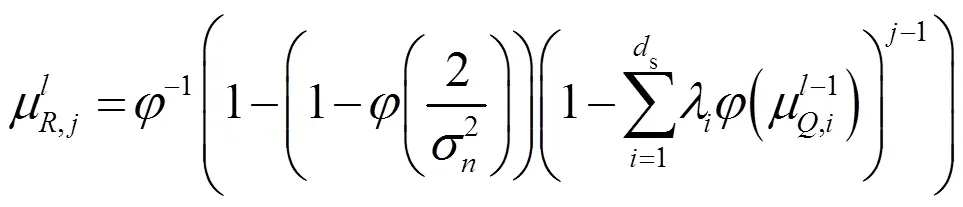
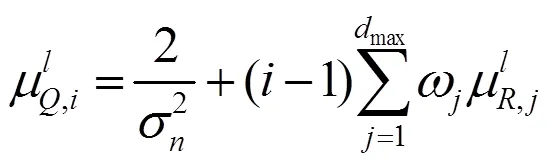
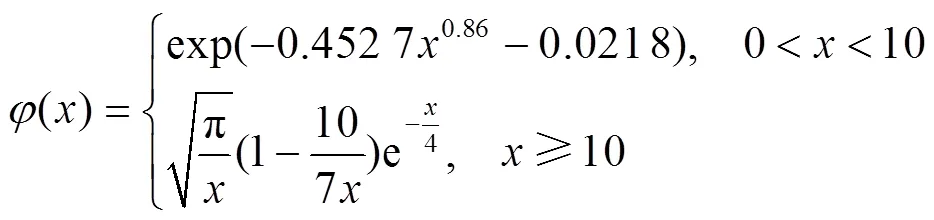
在此基础上，徐大专等[6]提出了AWGN信道下SLT码的度分布优化模型。

除了在AWGN信道上的研究，Paul等[37]还研究和分析了LT码在瑞利衰落（Rayleigh fading）和莱斯衰落（Rician fading）等信道中的适用性，提出了一种改进的度分布方法，以优化衰落信道下LT码的时延和误码率。Paul等[3]主要讨论了改变度为1的编码符号的比例对LT码时延和误码率的影响。结果表明，在瑞利衰落信道中，基于改进度分布的LT码在误码率和编译码时延方面有显著的改善。

3.1.3 分布式场景下的度分布

无速率编码以其优良的特性受到了越来越多的关注，而随着研究的深入，人们开始向无速率编码引入分布式研究。当把LT码应用于多信源单中继的网络，中继节点的异或操作会使接收端收到的度分布和原始编码器的度分布产生差异，最终导致BP算法难以有效地译码，产生较高的错误率。而如果在这种情况下使用GE算法，则会增加译码复杂度。

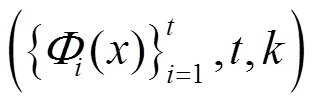
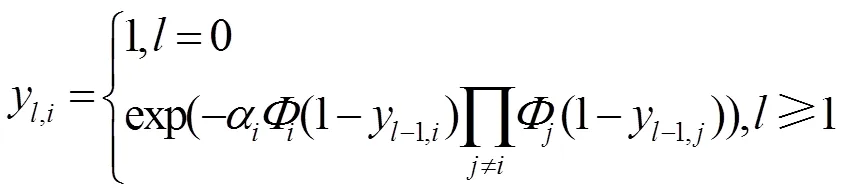
根据此密度演化方程可以指导度分布的优化。文献[38]提出类孤子分布无速率码用于无速率编码和网络编码的结合，而文献[39]在此基础上做了改进，形成了新的度分布。此类分布式下的喷泉码以及度分布的研究还有很多，然而它们都只适用于某种特殊情况，如两信源或四信源，并没有对信源和中继网络做整体优化。

根据各信源是否具有相同的度分布或者相同的接入信道容量，可以将多信源单中继网络分为同构网络和异构网络两种模型。同构网络可以看作异构网络的特例。为了将分布式喷泉码的度分布设计方案推广到一般的异构网络中，文献[40]提出了针对一般的多信源单中继网络的广义分布式喷泉码，并给出了总体的编码方案。异构网络中不同信源的译码失败率是不同的，因此在这种模型中网络喷泉码的度分布函数将不能使用形如点对点通信中数字喷泉码的一元度分布函数来表示，便提出了异构网络中多元度分布函数的概念，即：

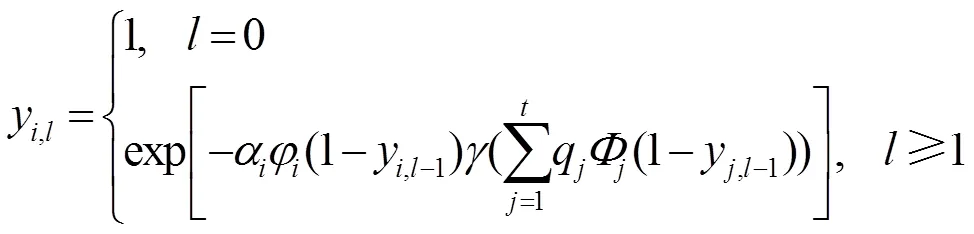
在异构网络中，信源和中继的度分布都会影响最终无速率编码的性能，因此可以采用分布联合设计的方法。根据式（17）中的多元密度演化方程组，可以给出异构网络的两步联合优化模型[40]。

中继度分布优化模型为：

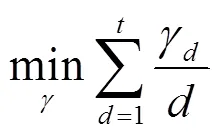
信源度分布优化模型为：

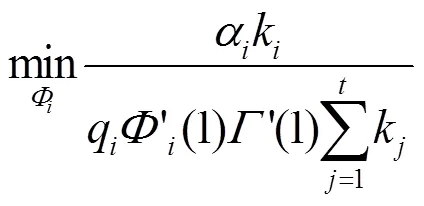
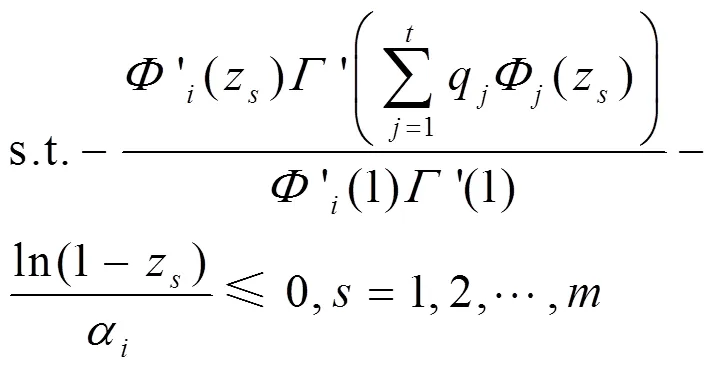
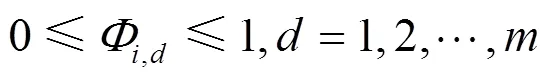
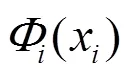
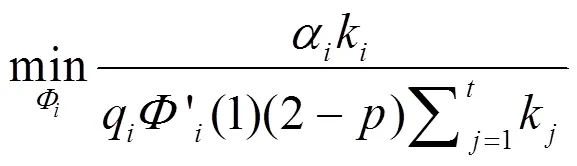
s.t.式（23）、式（24）

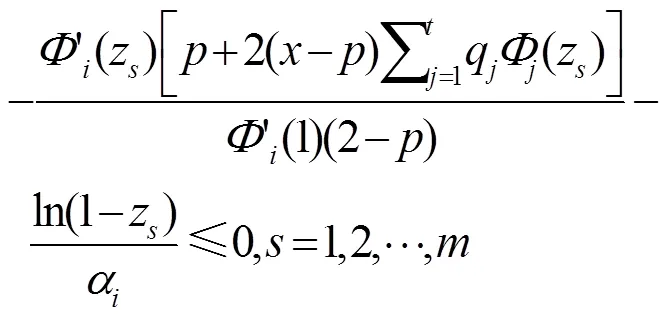
3.1.4 多路径场景与融合网络编码的度分布

由于喷泉码的无速率特性，喷泉码和多路径、喷泉码和网络编码结合的研究逐渐增多。然而在这些情况下，网络编码会对节点的度分布产生影响，导致接收端收到的符号度分布与原始信息度分布不同，降低译码成功率。因此，结合喷泉码与多路径或者网络编码时，可以考虑对度分布进行重新设计。

针对高时延高损耗的子流严重影响其他子流导致显著降低吞吐量的问题，提出简单的基于喷泉码的多路径结构[41]，如图2所示。利用喷泉码的灵活性，缓解了异构路径带来的负面影响。此外，文献[41]也基于喷泉码的特性进行了数据分配方案的优化设计。

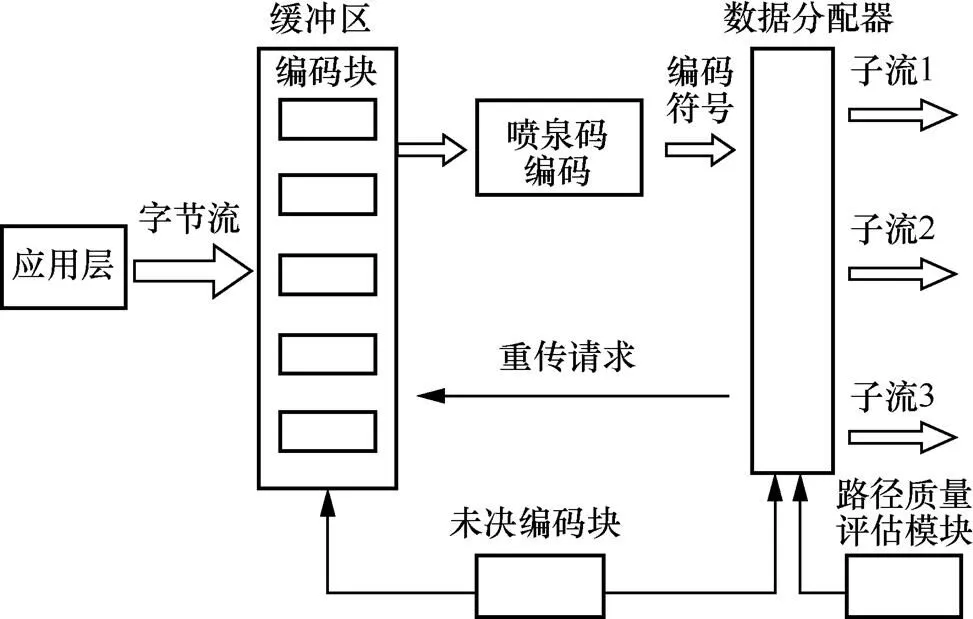
图2 基于喷泉码的多路径结构

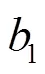
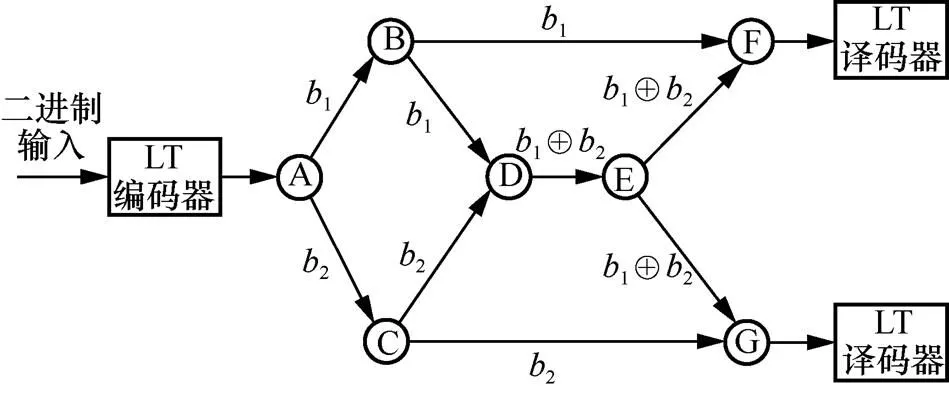
图3 结合喷泉码的蝶形网络编码

同时文献[43]也考虑了Raptor码经网络编码之后节点的度分布发生改变的问题。针对这个问题，文献[43]提出一个通过几何规划确定正则网络拓扑中适当的源度分布的通用优化问题，在设定完最终希望接收到的度分布函数后，反向推理出此时的原始节点度分布，即改进的度分布函数。最终仿真结果表明，该码的译码概率和3GPP中典型的Raptor码相近。在无速率编码中，如果对时延没有限制，译码中断概率会趋近于0，因此设计出无速率编码和网络编码的结合方法[44]，并以吞吐量而不是中断概率进行性能评估，最终实现机器与演进型基站之间的可靠通信。

3.2 不同优化目标的度分布

3.2.1 复杂度

度分布的优化可以将最小复杂度作为目标，这里的复杂度表示输出节点的平均度数。复杂度越高，译码时需要的译码操作数就越多，对时间以及资源的耗费就越大，因此通常会追求较低的译码复杂度。文献[32]提出了一种删除信道下的度分布优化模型，将最小化输出节点平均度数作为优化目标，将密度演化方程中每次迭代时无码率降低作为约束条件。

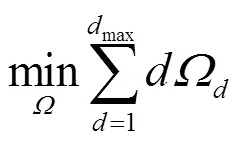
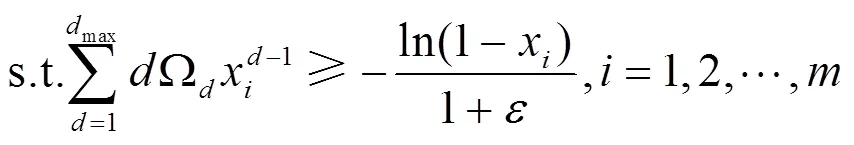
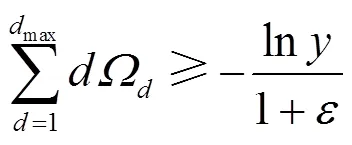
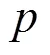
3.2.2 开销

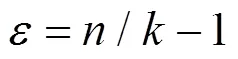
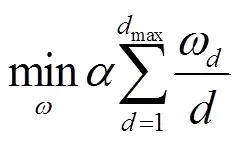
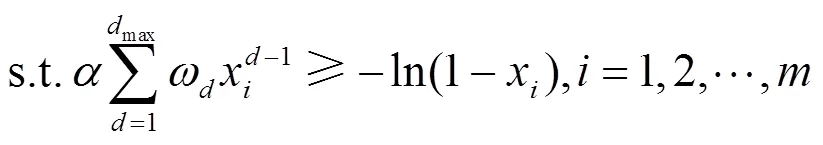
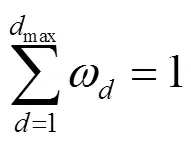
同样地，针对SLT码在删除信道以及AWGN信道下的优化问题，根据SLT码在两种信道下的密度演化方程（即式（9）和式（12）～式（13）），分别给出两种信道下以最小开销为目标的优化模型[6]。两种模型均只改变式（32）～式（34）中关于密度演化方程的约束条件，其中删除信道下的式（33）变为：

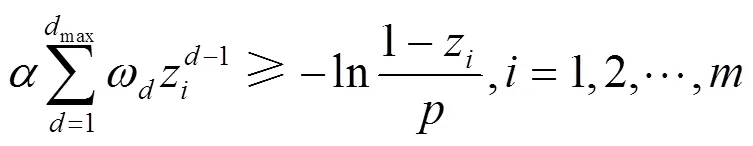
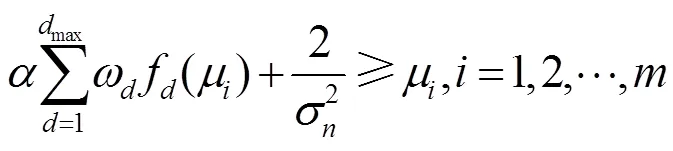
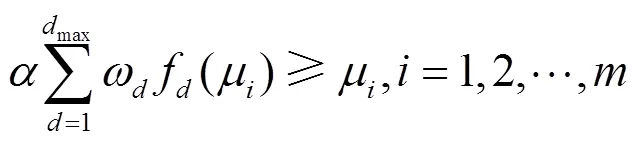
另外，开销和复杂度这两种优化目标均将密度演化方程推导出的译码成功率作为约束，求出最小开销或者最小复杂度的度分布函数。相反地，将约束和目标函数置换，就会很容易地得到另一种优化模型：将开销或者复杂度作为约束条件，求取能够达到最大译码成功率的度分布函数。例如，文献[45]中给出了短码长下以最大译码成功率为目标的度分布优化模型。因为只需要将约束条件和目标函数进行置换就可得到这样的优化模型，所以这里不展开介绍。

3.2.3 可译集大小

由于无速率编码的复杂度和开销严重影响编译码和传输的时间、资源消耗，无速率编码受到了广泛关注，被普遍作为度分布优化模型的优化标准。而除了这两个物理量，可译集大小的取值与波动情况也可以反映译码情况，因此也被当作度分布优化模型的优化标准。关于可译集的定义，在Luby[1]对LT码的介绍中有如下说明：如果信源符号已经被“释放”的编码符号恢复，但是这个信源符号还没有被“处理”，即这个信源符号还没有和相连的编码符号进行异或操作，则意味着此符号可译，称这类符号的集合为可译集。部分研究中也有提到输出可译集的概念，指在译码时度为1且还未“释放”的编码符号的集合。这两种概念虽然具体指代的内容不完全相同，但是其对译码过程的影响是大致相同的。无论是可译集还是输出可译集，当其大小在译码过程中变为0时，就表示BP算法失败，此时必须采用复杂度更高的GE算法。因此需要在译码过程中，保证可译集大小的均值以及方差，因此有了以可译集大小为优化目标的度分布优化模型。

从最早LT码中RSD的研究开始[1]，针对可译集的度分布优化就开始了，文献[46]给出了计算可译集大小的方法，为了获得更好的喷泉码性能，文献[47]基于可译集大小调整了个别度值的概率，文献[48]将可译集大小作为优化目标，求解了联合度分布的最佳比例。针对随机图法构造的LT码在中高码长下容易译码失败的问题，文献[49]基于可译集大小进行了优化，提出了改进的累积边增加法，提高了译码成功率。

对可译集大小的研究是从很早就开始的，最早的RSD也可以理解为一种以可译集大小为优化目标的度分布优化模型[1]。除了Luby认为的，译码过程中应保证可译集大小不变这一观点[1]，也有学者认为，为了减少不必要的开销，可译集大小应该随着译码的进行逐渐减小[50]。文献[50]提出了一种能够让可译集大小递减的设计程序，所提方法在平均开销和错误率方面的性能都有显著提高。

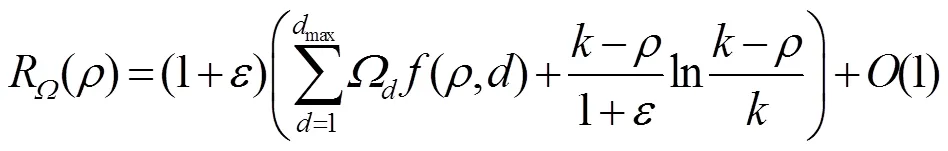
其中，

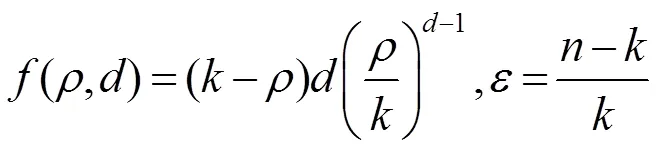
基于输出可译集调整了编码时度为1、度为2和最大度值的概率，提出了改进的鲁棒孤波分布（modified robust soliton distribution，MRSD）[47]。文献[47]将增大可译集大小的均值、降低其方差转化为一个最大化问题，同时也引入序列二次规划算法来求解目标函数。结果表明，通过选择参数，MRSD比RSD有更高的译码成功率。此外，与其他优化分布相比，应用了MRSD的无速率编码，要么有较低的输出符号平均度数，要么需要更少的译码开销。文献[52]也通过类似方法优化可译集大小，进而优化度分布函数，对取得特定度值的概率进行修改，最终得到的度分布在短码长时也有较好的性能。

由于可译集大小的均值和方差可以表示无速率编码编译码时的性能，基于这一特性设计了度分布的优化算法[48]。以可译集大小的均值和方差为优化标准，求解一种PD和RSD结合的联合度分布的最优比例。针对在中高码率下使用随机图法构造的LT码有一定概率译码失败的缺点，提出一种改进的累积边增加法，能够通过控制可译集大小保证译码成功率[49]。文献[49]分析了可译集大小和度分布的关系，并基于此对原始方法进行改进，实验结果表明，与传统随机图法构造的LT码相比，经过改进的LT码性能得到了显著提高。

3.3 度分布优化方法分析总结

3.3.1 针对单一度分布应用问题的度分布优化

LT码下，ISD在实际应用中很容易出现译码失败的情况，而RSD有更高的容错率，在码长较长时具有较理想的性能，一直被当作理论研究的对象，但是其只能生成少量的小度值的编码分组，随着码长的降低，RSD的性能下降非常明显，采用BP译码很容易译码失败。针对RSD的这一不足，Agha等[31]提出了BED。和RSD相比，BED增加了生成小度值编码分组的概率，但是降低了大度值编码分组的数量，提高了源数据不能得到良好的覆盖从而被遗露的可能。类似的还有泊松分布，通过对PD中参数的设定，理论上PD在小度值的性能方面比BED更好，但是PD有着和BED同样的问题，即生成了过多小度值编码分组，而大度值编码分组数量不足，从而遗露部分源数据。

除了针对单一度分布的处理优化，研究人员也尝试将性能互补的度分布结合，以提升喷泉码的编译码性能。于是有了两种结合不同度分布优点的新的度分布——开关度分布以及联合度分布。这两种度分布都由多种经典度分布的结合产生，开关度分布中存在开关点，通过判断是否达到开关点来切换编码时服从的度分布；联合度分布将多种度分布进行求和，用比例系数控制各个度分布在整个联合度分布中的占比。相比基于单一度分布的喷泉码，基于开关度分布或联合度分布的喷泉码有更好的编译码性能。常见的度分布的结合有BED和RSD[52-55]、PD和RSD[48, 56]等。

针对译码初期由于小度值编码分组过少而容易译码中断的问题，文献[53]给出了一种结合BED和RSD的开关度分布。这种度分布集成了BED和RSD的优点，在编码时，会生成较多小度值编码数据包，便于接收端更顺利地进行译码初期的任务。另外，采用这种开关度分布后只需要很少的编码包就可以完成译码。这种开关度分布的计算式为：

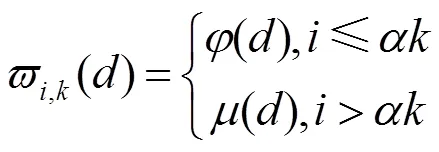
同样地，文献[54]先对BED和RSD两种度分布进行处理，再将两者以开关度分布的形式结合，以实现度分布的优化。文献[52]也是先对BED进行调整，然后结合RSD，再通过优化译码时的可译集大小来优化度分布函数，最终得到一种在短码长下也有较好性能的度分布。文献[57]引入改进后的幂律分布，将其与RSD结合，采用文献[47]提出的方法求解结合比例。文献[55]通过一种仿生算法在BED和RSD之间随机游走，寻找更优的度分布概率取值。

为了引入PD，文献[56]将调整后的PD与RSD直接相加并归一化，最终得到一个新的联合度分布，新的度分布弥补了RSD生成小度值编码包概率偏低的问题，提高了译码成功率；基于输出可译集的特性，文献[48]设计了优化算法用于求解PD和RSD结合的最优比例，得到新的度分布。仿真结果表明，相较于RSD，采用优化后的度分布的喷泉码性能显著提升。

3.3.2 针对码长问题的度分布优化

早期的度分布研究大多是在长码长的情况下进行的，然而在某些实际的应用场合中码长是会不断变化的，这会对喷泉码的编译码产生影响。而且实际中大多是短码长，而许多度分布在短码长下性能下降十分明显。例如当码长较短时，RSD虽然能生成很多大度值的编码分组，但是由于小度值的编码分组过少，用BP译码很容易失败，而再使用GE译码会有巨大的开销。因此，考虑到实际应用中不同码长信息对喷泉码的需求，设计了截短度分布、固定度分布以及其他一些针对码长问题的度分布。

在实际应用中，喷泉码的码长是会发生变化的，这会对编译码的复杂度产生影响，例如当RSD应用在LT码中，随着码长的增加，RSD生成编码分组的平均度值增大，从而使编译码复杂度提高。针对这一问题，在长期的工程应用实践中，人们总结出一类有很强实用性的、与码长无关的度分布函数，称之为固定度分布。固定度分布的平均度值固定不变，不会因为码长的变化而变化。比如泊松分布就是一类固定度分布：

这种度分布应用在LT码中时，平均度值固定为5.870 3，其编译码的复杂度与码长呈线性关系。这样的固定度分布同样适用于长码长，消除了码长变化对编译码复杂度造成的影响，但是当码长太短时，仍然容易出现译码失败的情况。

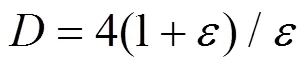
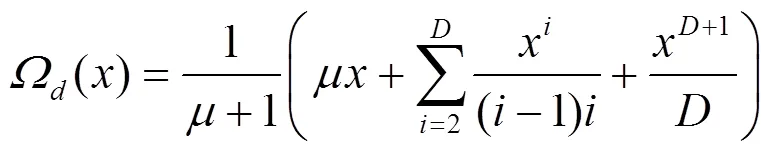
针对喷泉码在短码长下的应用问题，许多学者提出了自己的优化方法。例如，用一种开关度分布解决短码长下喷泉码译码成功率降低的问题[58]；提出性能模型，并采用了3种进化策略[59]；对截短度分布进行改进[60]；提出一种扩展窗-喷泉码的方案[61]。

文献[58]首先针对采用RSD、固定度分布和截短度分布的喷泉码进行了性能分析和仿真，得到了不同码长下这几种度分布的性能情况。之后改进了一种适用于短码长的度分布，这一度分布实际上是一种开关度分布，当未译码符号数低于某个阈值时，度分布就会由原本的RSD转变为文献[58]中设计的与未译码符号数相关的新的度分布。实验结果表明，在相同的译码开销下，相比传统的截短度分布，改进后的度分布应用在短码长时译码成功率会有很大的提升。

Zao等[59]构建了一种新的性能模型，并提出了度分布优化方案，该模型考虑了编码开销、未覆盖符号比率和译码失败率3种因素。在优化时，提供3种已知的进化策略寻求最优度分布，最终优化短码长下喷泉码的性能。实验结果表明，3种进化策略都能得到最优的度分布。

李杰[60]采用与传统截短度分布不同的方式进行截短。ISD和RSD的度值序列根据引入的两个门限值以及权重进行截短，根据优化算法，求出度分布函数中每个度值的最优概率，得到最优度分布，提高了译码性能。

文献[61]给出了一种扩展窗-喷泉码的方案，提出Raptor的外码采用低码率的LDPC码和度分布，这样在短码长的情况下会比高码率的外码有更低的译码开销。同时介绍了码长不同时，如何为预编码选择合适的度分布以及码率。

3.3.3 基于部分信息的度分布优化

喷泉码的出现是为了减少反馈重传，从而有效降低时延，减少资源消耗，防止“反馈风暴”的发生。然而从信息论的角度来看，喷泉码接收端的反馈信息的确可以给编码进行辅助，有利于提高喷泉码的性能。现有喷泉码和理想中的喷泉码相比，有着较大的译码开销，仍然有待改进。为了对现有喷泉码进行优化，一些学者提出基于反馈信息的喷泉码，在喷泉码编码时利用少量反馈信息，以此降低译码开销。

为了在喷泉码中有效地利用反馈信息，文献[62]提出基于反馈的实时纠错方法，分析表明，利用反馈信息的喷泉码可以有效降低喷泉码的译码开销。也有学者提出根据可译集大小调整反馈信息，以此修正度分布函数，减少译码开销[50,63]。文献[64]提出有多次反馈的喷泉码，根据接收到的编码符号平均度发送反馈信息，以此修正度分布函数。

文献[65]提出一种基于部分信息的喷泉码，发送端根据接收端已知的信源符号数对RSD进行调整，以此减少译码开销。文献[65]将修正后的RSD称为转移RSD（shifted robust soliton distribution，SRSD）。

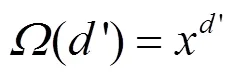
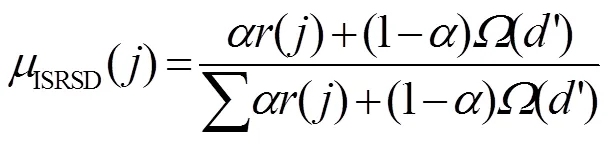
3.3.4 未知先验信息的度分布优化

不同的应用环境对度分布有不同的需求，在设计度分布时，往往需要知道关于环境的先验知识，然而当环境信息（如码长、信道信息等）难以获取时，就难以针对性地设计出合适的度分布。针对这一问题，Savchenko等[67]提出用深度强化学习来近似/学习基于LT码的最优度分布的优化方法。该方法在其意义上是简单的，不需要复杂的分析，它能够通过输入符号的数量和预期接收开销来参数化度分布，这里的预期接收开销不一定是实际接收开销。实验结果表明，采用该方法学习的度分布的LT码在译码效率和编译码复杂度方面均优于其他方法。与其他优化方法相比，基于深度强化学习的优化方法有几个优点，比如能够泛化到不可见的数据，以及近似复杂非线性映射的能力。该方法不需要任何关于应用环境的先验知识，因此，它可以直接应用于任何基于LT码的版本，具有很好的泛化性。文献[68]使用强化学习的方法对一般的纠错编码进行设计，其中涉及线性分组码和极化码，但是并未对LT码、Raptor码等喷泉码进行深入探讨。目前在未知先验信息的度分布优化上的研究还相对较少，有待更深入的研究。

3.4 度分布研究的挑战与展望

目前来看，对度分布的设计与优化已经较为系统，对多种信道场景和优化目标均有讨论研究，但是仍然存在一些不足，还有许多理论和技术问题亟待解决。

（1）无速率编码的译码成功率和度分布存在对应关系，理论上存在译码成功率和度分布之间的换算，但是目前尚未找到计量精确且计算量低的计算方法。因此，对译码成功率和度分布之间关系的建模仍有待深入研究。

（2）目前的度分布优化方法大多建立在密度演化的渐进性能分析上，然而这种方法并不能很好地适配有限长码字的情况。虽然当前已经有针对短码长下度分布的优化，但是整体的效果仍有待提高。因此需要找到一种新的针对有限长码字的性能分析方法，针对短码长下的度分布进行系统性的优化。

（3）随着无速率编码的广泛应用，度分布也势必需要适配各种场景与需求。例如，针对不等差错保护的无速率编码研究[69]，以及无速率编码在物联网中的应用，文献[29]介绍了针对物联网的应用层编码有哪些优势以及限制；而针对工业控制系统中有界时延的问题，文献[30]对多种喷泉码进行了对比实验，分析发现喷泉码的性能在有界时延和无时延要求下有很大的不同。同时，无速率编码在各种场景下的具体应用，都会对度分布产生新的要求，因此在更广泛、更具体的应用场景下，如何针对性地进行度分布的设计与优化，仍需要持续地研究与探索。深度学习和度分布的结合也为度分布的优化提供了新思路，当应用场景和需求变化时，可以很快地适配新的环境，也值得进一步的研究。

4 结束语

从无速率编码首次提出至今，研究成果丰硕。从最初的LT码、Raptor码，到当前的OFC和BATS码，无速率编码的性能逐渐提高，应用领域也逐渐扩展，其在广播通信、车联网、分布式计算等场景中都有很大的应用潜力。而随着应用场景的变化，对无速率编码的需求也不尽相同，此时度分布也需要做出改进。本文从无速率编码的发展和应用开始，介绍了各种无速率编码的特点和优势，总结了不同技术在多个领域的应用。针对度分布的设计与优化问题，首先从删除信道、无线信道等不同场景进行分类介绍，之后从复杂度、开销、可译集大小3个方面介绍度分布的优化目标，最后，从无速率编码实际应用中可能存在的问题出发，包括单一度分布存在的问题、码长问题、未知先验信息的问题等，对目前已有的解决方法做出总结和分析。希望能从整体对度分布有什么问题、优化什么、如何优化进行探讨，为相关研究人员提供借鉴。随着无速率编码的广泛应用，对度分布的研究也需要与时俱进，需要与具体的应用环境和需求相适配，比如在工业控制环境以及物联网下的应用等，因此，后续仍然需要对度分布进行更深入的研究。

[1] LUBY M G. LT codes[C]//Proceedings of 43rd Annual IEEE Symposium on Foundations of Computer Science. Piscataway: IEEE Press, 2002: 271-280.

[2] SHOKROLLAHI A. Raptor codes[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2551-2567.

[3] SHIRVANIMOGHADDAM M, LI Y H, VUCETIC B. Adaptive analog fountain for wireless channels[C]//Proceedings of 2013 IEEE Wireless Communications and Networking Conference. Piscataway: IEEE Press, 2013: 2783-2788.

[4] YANG S H, YEUNG R W. Batched sparse codes[J]. IEEE Transactions on Information Theory, 2014, 60(9): 5322-5346.

[5] LÁZARO F, LIVA G, BAUCH G. Inactivation decoding of LT and raptor codes: analysis and code design[J]. IEEE Transactions on Communications, 2017, 65(10): 4114-4127.

[6] 徐大专, 许生凯, 华洁, 等. 数字喷泉码度分布优化设计的最新研究进展[J]. 数据采集与处理, 2015, 30(4): 733-746.

XU D Z, XU S K, HUA J, et al. Recent progress on optimization design of degree distributions in digital fountain codes[J]. Journal of Data Acquisition and Processing, 2015, 30(4): 733-746.

[7] MACKAY D J C. Fountain codes[J]. IEE Proceedings - Communications, 2005, 152(6): 1062.

[8] 黄靖轩, 费泽松, 李欢. 无速率编码及其应用综述[J]. 无线电通信技术, 2020, 46(1): 44-54.

HUANG J X, FEI Z S, LI H. Overview of rateless codes and their applications[J]. Radio Communications Technology, 2020, 46(1): 44-54.

[9] LUBY M G, MITZENMACHER M, SHOKROLLAHI M A. Analysis of random processes via AND-OR tree evaluation[C]//Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms. [S.l.:s.n.], 1998.

[10] ETESAMI O, SHOKROLLAHI A. Raptor codes on binary memoryless symmetric channels[J]. IEEE Transactions on Information Theory, 2006, 52(5): 2033-2051.

[11] TANNER R. A recursive approach to low complexity codes[J]. IEEE Transactions on Information Theory, 1981, 27(5): 533-547.

[12] 3GPP. Multimedia broadcast/multicast service(MBMS); protocols and codecs: TS 26. 346 V7. 2. 0[S]. 2006.

[13] ETSI T S. IP datacast over DVB-H: content delivery protocols: 102 472 v1. 2. 1[S]. 2006.

[14] JEON S Y, AHN J H, LEE T J. Reliable broadcast using limited LT coding in wireless networks[J]. IEEE Communications Letters, 2016, 20(6): 1187-1190.

[15] BORKOTOKY S S, PURSLEY M B. Fountain-coded broadcast distribution in multiple-hop packet radio networks[J]. IEEE/ACM Transactions on Networking, 2019, 27(1): 29-41.

[16] PALMA V, MAMMI E, VEGNI A M, et al. A fountain codes-based data dissemination technique in vehicular Ad-hoc networks[C]//Proceedings of 2011 11th International Conference on ITS Telecommunications. Piscataway: IEEE Press, 2011: 750-755.

[17] ABDULLAH N F, DOUFEXI A, PIECHOCKI R J. Raptor codes-aided relaying for vehicular infotainment applications[J]. IET Communications2013, 7(18): 2064-2073.

[18] GAO Y M, XU X L, GUAN Y L, et al. V2X content distribution based on batched network coding with distributed scheduling[J]. IEEE Access, 2017(6): 59449-59461.

[19] ANGLANO C, GAETA R, GRANGETTO M. Exploiting rateless codes in cloud storage systems[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(5): 1313-1322.

[20] LU H F, FOH C H, WEN Y G, et al. Delay-optimized file retrieval under LT-based cloud storage[J]. IEEE Transactions on Cloud Computing, 2017, 5(4): 656-666.

[21] OKPOTSE T, YOUSEFI S. Systematic fountain codes for massive storage using the truncated Poisson distribution[J]. IEEE Transactions on Communications, 2019, 67(2): 943-954.

[22] 段文雪, 胡铭, 周琼, 等. 云计算系统可靠性研究综述[J]. 计算机研究与发展, 2020, 57(1): 102-123.

DUAN W X, HU M, ZHOU Q, et al. Reliability in cloud computing system: a review[J]. Journal of Computer Research and Development, 2020, 57(1): 102-123.

[23] PUDUCHERI S, KLIEWER J, FUJA T E. The design and performance of distributed LT codes[J]. IEEE Transactions on Information Theory, 2007, 53(10): 3740-3754.

[24] HUSSAIN I, XIAO M, RASMUSSEN L K. Buffer-based distributed LT codes[J]. IEEE Transactions on Communications2014, 62(11): 3725-3739.

[25] SUN L, REN P Y, DU Q H, et al. Fountain-coding aided strategy for secure cooperative transmission in industrial wireless sensor networks[J]. IEEE Transactions on Industrial Informatics, 2016, 12(1): 291-300.

[26] YI B S, XIANG M, HUANG T Q, et al. Data gathering with distributed rateless coding based on enhanced online fountain codes over wireless sensor networks[J]. AEU - International Journal of Electronics and Communications, 2018, 92: 86-92.

[27] YUE J, XIAO M, PANG Z B. Distributed fog computing based on batched sparse codes for industrial control[J]. IEEE Transactions on Industrial Informatics, 2018, 14(10): 4683-4691.

[28] SEVERINSON A, AMAT A G I, ROSNES E. Block-diagonal and LT codes for distributed computing with straggling servers[J]. IEEE Transactions on Communications, 2019, 67(3): 1739-1753.

[29] SANDELL M, RAZA U. Application layer coding for IoT: benefits, limitations, and implementation aspects[J]. IEEE Systems Journal, 2019, 13(1): 554-561.

[30] YUAN M Y, FU Y S, QIAO Y, et al. Rateless codes for reliable and secure packet transmission in industrial control systems[C]//Proceedings of 2021 China Automation Congress (CAC). Piscataway: IEEE Press, 2021: 6376-6381.

[31] AGHA K A, KADI N, STOJMENOVIC I. Fountain codes with XOR of encoded packets for broadcasting and source independent backbone in multi-hop networks using network coding[C]//Proceedings of IEEE 69th Vehicular Technology Conference. Piscataway: IEEE Press, 2009: 1-5.

[32] SEJDINOVIC D, PIECHOCKI R J, DOUFEXI A. AND-OR tree analysis of distributed LT codes[C]//Proceedings of 2009 IEEE Information Theory Workshop on Networking and Information Theory. Piscataway: IEEE Press, 2009: 261-265.

[33] ZENG M, CALDERBANK R, CUI S G. On design of rateless codes over dying binary erasure channel[J]. IEEE Transactions on Communications, 2012, 60(4): 889-894.

[34] TSAI P C, CHEN C M, CHEN Y P. A novel evaluation function for LT codes degree distribution optimization[C]//Proceedings of 2014 IEEE Congress on Evolutionary Computation. Piscataway: IEEE Press, 2014: 3030-3035.

[35] NGUYEN T D, YANG L L, HANZO L. Systematic Luby transform codes and their soft decoding[C]//Proceedings of 2007 IEEE Workshop on Signal Processing Systems. Piscataway: IEEE Press, 2007: 67-72.

[36] WIBERG N . Codes and decoding on general graphs[D]. Linkoping: Linkoping University, 1996.

[37] PAUL I J L, RADHA S, RAJA J. Studies on the suitability of LT codes with modified degree distribution (MDD) for fading channels[C]//Proceedings of 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI). Piscataway: IEEE Press, 2014: 1764-1769.

[38] LIAU A, YOUSEFI S, KIM I M. Binary soliton-like rateless coding for the Y-network[J]. IEEE Transactions on Communications, 2011, 59(12): 3217-3222.

[39] LIAU A, KIM I M, YOUSEFI S. Improved low-complexity soliton-like network coding for a resource-limited relay[J]. IEEE Transactions on Communications, 2013, 61(8): 3327-3335.

[40] SHAO H Q, XU D Z, ZHANG X F. Asymptotic analysis and optimization for generalized distributed fountain codes[J]. IEEE Communications Letters, 2013, 17(5): 988-991.

[41] CUI Y, WANG L, WANG X, et al. FMTCP: a fountain code-based multipath transmission control protocol[J]. IEEE/ACM Transactions on Networking, 2015, 23(2): 465-478.

[42] LIMMANEE A, HENKEL W. A cooperative scheme for shaping degree distribution of LT-coded symbols in network coding multicast[C]//Proceedings of 2010 International ITG Conference on Source and Channel Coding (SCC). Piscataway: IEEE Press, 2010: 1-6.

[43] THOMOS N, FROSSARD P. Degree distribution optimization in Raptor network coding[C]//Proceedings of 2011 IEEE International Symposium on Information Theory Proceedings. Piscataway: IEEE Press, 2011: 2736-2740.

[44] NESSA A, KADOCH M. Joint network channel fountain schemes for machine-type communications over LTE-advanced[J]. IEEE Internet of Things Journal, 2016, 3(3): 418-427.

[45] HYYTIA E, TIRRONEN T, VIRTAMO J. Optimal degree distribution for LT codes with small message length[C]//Proceedings of IEEE INFOCOM 2007 - 26th IEEE International Conference on Computer Communications. Piscataway: IEEE Press, 2007: 2576-2580.

[46] MAATOUK G, SHOKROLLAHI A. Analysis of the second moment of the LT decoder[C]//Proceedings of 2009 IEEE International Symposium on Information Theory. Piscataway: IEEE Press, 2009: 2326-2330.

[47] YEN K K, LIAO Y C, CHEN C L, et al. Modified robust soliton distribution (MRSD) with improved ripple size for LT codes[J]. IEEE Communications Letters, 2013, 17(5): 976-979.

[48] 戴新颖, 王建萍. 基于输出可译集的LT码联合度分布优化[J].系统工程与电子技术, 2020, 42(3): 727-732.

DAI X Y, WANG J P. Optimization of combined degree distribution of LT codes based on output ripple size[J]. Systems Engineering and Electronics, 2020, 42(3): 727-732.

[49] 郑志国, 侯登峰. 基于可译集大小的LT码编码算法的改进[J]. 电视技术, 2011, 35(5): 13-16.

ZHENG Z G, HOU D F. Improvement of LT encoding algorithm based on ripple size[J]. Video Engineering, 2011, 35(5): 13-16.

[50] RENSEN J H S, POPOVSKI P, OSTERGAARD J. Design and analysis of LT codes with decreasing ripple size[J]. IEEE Transactions on Communications, 2012, 60(11): 3191-3197.

[51] YEN K K, LIAO Y C, CHANG H C. Design of LT code degree distribution with profiled output ripple size[C]//Proceedings of 2015 IEEE Workshop on Signal Processing Systems (SiPS). Piscataway: IEEE Press, 2015: 1-6.

[52] 雷维嘉, 张梦, 谢显中. 基于度分布合并和可译集优化的LT码度分布设计方案[J]. 电子学报, 2015, 43(4): 800-805.

LEI W J, ZHANG M, XIE X Z. A design scheme for LT codes degree distribution by combining degree distributions and optimizing ripple size[J]. Acta Electronica Sinica, 2015, 43(4): 800-805.

[53] ZHANG M, LEI W J, XIE X Z. Combined degree distribution: a simple method to design the degree distribution of fountain codes[C]//Proceedings of 2013 IEEE Third International Conference on Information Science and Technology. Piscataway: IEEE Press, 2013: 1089-1092.

[54] 任鹏, 相征. LT码中一种新的开关度分布[J]. 西安电子科技大学学报, 2015, 42(5): 43-47.

REN P, XIANG Z. New switch degree distribution for the LT code[J]. Journal of Xidian University, 2015, 42(5): 43-47.

[55] 姚渭箐, 胡凡. 基于IBED和仿生算法的LT码度分布设计[J]. 电子学报, 2019, 47(2): 428-433.

YAO W Q, HU F. The design of degree distribution for LT codes based on IBED and bionic algorithm[J]. Acta Electronica Sinica, 2019, 47(2): 428-433.

[56] YAO W Q, YI B S, HUANG T Q, et al. Poisson robust soliton distribution for LT codes[J]. IEEE Communications Letters, 2016, 20(8): 1499-1502.

[57] 龚赟, 王俊义. 一种用于LT码的新型联合度分布设计方法[J]. 桂林电子科技大学学报, 2017, 37(5): 355-360.

GONG Y, WANG J Y. A design method of novel combined degree distribution for LT code[J]. Journal of Guilin University of Electronic Technology, 2017, 37(5): 355-360.

[58] 敖珺, 卢亚军, 马春波. 基于短码长的喷泉码度分布设计[J]. 计算机与数字工程, 2015, 43(12): 2101-2105.

AO J, LU Y J, MA C B. Fountain codes degree distribution design based on short code length[J]. Computer & Digital Engineering, 2015, 43(12): 2101-2105.

[59] ZAO J K, HORNANSKY M, DIAO P L. Design of optimal short-length LT codes using evolution strategies[C]//Proceedings of 2012 IEEE Congress on Evolutionary Computation. Piscataway: IEEE Press, 2012: 1-9.

[60] 李杰. 无线传输中短码长喷泉码的度分布优化算法[J]. 电讯技术, 2016, 56(8): 900-905.

LI J. A degree distribution optimization algorithm for small size fountain codes in wireless transmission[J]. Telecommunication Engineering, 2016, 56(8): 900-905.

[61] YUAN L, DENG K Y, LI H A. Design of finite-length precoded EWF codes for scalable video streaming[J]. Wireless Personal Communications, 2017, 97(3): 4111-4128.

[62] BEIMEL A, DOLEV S, SINGER N. RT oblivious erasure correcting[J]. IEEE/ACM Transactions on Networking, 2007, 15(6): 1321-1332.

[63] JIA D, FEI Z S, SHANGGUAN C L, et al. LT codes with limited feedback[C]//Proceedings of 2014 IEEE International Conference on Computer and Information Technology. Piscataway: IEEE Press, 2014: 669-673.

[64] HAGEDORN A, AGARWAL S, STAROBINSKI D, et al. Rateless coding with feedback[C]//Proceedings of IEEE INFOCOM 2009. Piscataway: IEEE Press, 2009: 1791-1799.

[65] AGARWAL S, HAGEDORN A, TRACHTENBERG A. Adaptive rateless coding under partial information[C]//Proceedings of 2008 Information Theory and Applications Workshop. Piscataway: IEEE Press, 2008: 5-11.

[66] 牛芳琳, 李宝明, 陈付亮, 等. 一种改进的基于部分信息喷泉码度分布设计[J]. 电子学报, 2016, 44(2): 295-300.

NIU F L, LI B M, CHEN F L, et al. The improved degree distribution for rateless code under partial information[J]. Acta Electronica Sinica, 2016, 44(2): 295-300.

[67] SAVCHENKO Y, LIU Y. Optimizing degree distributions of LT-based codes with deep reinforcement learning[C]//Proceedings of IEEE INFOCOM 2019 - IEEE Conference on Computer Communications Workshops. Piscataway: IEEE Press, 2019: 228-233.

[68] HUANG L C, ZHANG H Z, LI R, et al. AI coding: learning to construct error correction codes[J]. IEEE Transactions on Communications, 2020, 68(1): 26-39.

[69] 宋鑫, 倪淑燕, 张喆, 等. 面向不等差错保护的低误码平台LT编码算法[J]. 通信学报, 2022, 43(6): 85-97.

SONG X, NI S Y, ZHANG Z, et al. Low error floor LT coding algorithm for unequal error protection[J]. Journal on Communications, 2022, 43(6): 85-97.

Research and development of degree distribution in the rateless code

QIAO Yue1,2, FU Yusun2,3,4, YUAN Muyun1,2, TANG Jinhui2

1. Ningbo Artificial Intelligence Institute of Shanghai Jiao Tong University, Ningbo 315000, China 2. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China 3. Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China 4. Shanghai Engineering Research Center of Intelligent Control and Management, Shanghai 200240, China

As a kind of deletion coding technology, the rateless code reduces feedback retransmission and has the characteristics of flexible bit rate and simple compilation code, which has broad application prospects in many fields. As the basis of rateless code design, degree distribution has a crucial impact on the performance of the rateless code With the wide application of the rateless code, the design of degree distribution also needs to change with changes in scenarios and needs. Firstly, the development and application of the rateless code were discussed. Starting with several classical rateless codes and degree distributions, the current research and development of the degree distribution were summarized and analyzed from three perspectives of application scenarios, optimization targets and existing optimization methods. Finally, the development and application trend of rateless codes and degree distribution were discussed.

rateless code, fountain code, degree distribution, network coding, multipath

TN911

10.11959/j.issn.1000−0801.2022268

2022−04−26；

2022−10−08

伏玉笋，fu_yusun@sina.com

国家重点研发计划项目（No.2019YFB1705703）；宁波市重大科技任务攻关项目（No.2021Z022）

The National Key Research and Development Program of China (No.2019YFB1705703), The Major Scientific and Technological Research Program of Ningbo (No.2021Z022)