基于遗传算法的过程挖掘隐私保护方法
2022-11-07高俊涛闫駪艺
高俊涛,闫駪艺
(东北石油大学 计算机与信息技术学院,黑龙江 大庆 163318)
1 问题的提出
事件日志包括流程的活动执行情况和丰富的上下文信息,基于事件日志进行过程挖掘不仅能够发现过程的控制流模型,还能提供对业务流程的多维分析。然而,某些应用场景下的事件日志包含高度敏感的隐私数据,无法直接应用过程挖掘技术[1]。例如医院患者的诊疗事件日志既蕴藏着宝贵的医疗过程知识,又包含着患者的个人隐私,流程一旦涉及手动处理,就可能暴露特定个人的隐私。表1所示为来自某医院信息系统的事件日志,假设攻击者仅知道某个患者进行了活动r和e,根据该日志数据很容易推断出实例4记录了该患者的诊疗过程,患者的诊疗活动和敏感属性值都将暴露。近几年,随着隐私相关法律法规的逐步健全,过程挖掘领域的隐私保护问题受到越来越广泛的关注。
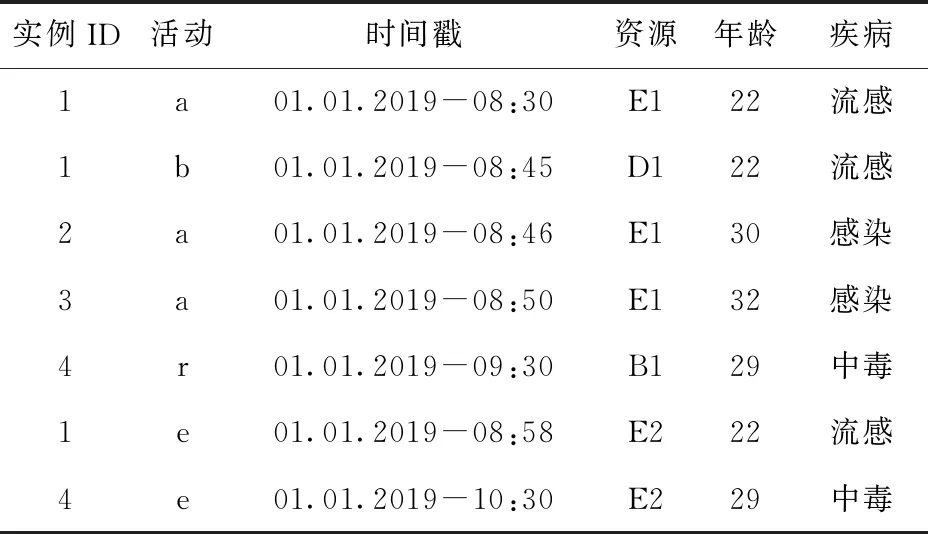
表1 事件日志
过程挖掘领域早期的隐私保护方法主要采用加密技术[2-4]实现。在给定少量背景知识的情况下,即使日志完全加密,仍可能导致隐私泄漏[5]。近年来,研究人员开始将数据失真技术和匿名化技术应用在过程挖掘领域,以抵御常见的攻击[6-7]。MANNHARDT等[1]将差分隐私概念应用于事件数据,以确保攻击者不能识别属于特定个人的数据;FAHRENKROG-PETERSEN等[8]将传统的隐私保护模型K-匿名和T-闭合组合,通过抑制的方式抵御链接攻击。无论采用哪种隐私保护技术,事件日志的效用都不可避免地受到损失。因此,如何在给定隐私要求下尽可能高地保留日志效用,是目前过程挖掘中隐私保护的主要问题。
针对上述问题,ELKOUMY等[9]研究了差分隐私参数的优化方法以获取更高的效用,为过程挖掘的差分隐私保护技术提供了效用优化方案;RAFIEI等[10]提出TLKC隐私保护模型,并采用贪心算法搜索符合隐私要求的活动抑制集,然而该方法存在以下问题:
(1)贪婪算法每次选择一个当前贪婪分数最高的活动放入抑制集,忽略了活动抑制的组合效应,容易陷入局部最优解。
(2)贪婪分数的计算方式过于简单,不能真实反映活动抑制对日志效用的影响,而且分辨精度不够,导致贪婪分数相同的活动大量存在,难以选择抑制活动。
(3)效用评价主要依靠匿名模型的质量,如F1-分数评估。然而模型质量并不能说明日志效用的保留情况,正确的隐私保护目标是得到与原始日志尽可能相似的结果。
本文提出一种基于遗传算法的隐私保护方法搜索活动抑制集,主要贡献包括:
(1)以活动抑制集为种群个体,将遗传算法引入过程挖掘隐私保护,从而获得高效用事件日志,同时通过改进遗传算子有效避免结果陷入局部最优。
(2)证明活动抑制集可行性的必要条件和约简规则,缩小遗传算法搜索空间。
(3)设计基于效用的适应度函数,以效用引导种群进化过程,为活动抑制集的选择提供合理的决策,保留更多的轨迹变体。
(4)将匿名模型与原模型的平均绝对误差作为评价指标,直观反映匿名日志的效用。
2 相关工作
目前,在过程挖掘领域主要存在加密、差分隐私和匿名化3类隐私保护技术,本章对这3类隐私保护技术在过程挖掘领域的应用及发展现状进行分析。
BURATTIN等[2]提出一种基于高级加密标准(Advanced Encryption Standard, AES)和Paillier密码系统的加密方案,该方案允许过程挖掘外包,并确保数据集和过程的机密性;TILLEM等[11]提出一种应用加密协议的Alpha算法进行过程发现,该方法能够同时保证用户和软件的隐私;RAFIEI等[5]提出一种受控的隐私保护方式,未经授权的用户不得访问高级别的机密信息,同年又提出一个框架,为过程挖掘的机密性提供了通用的解决方案[4],然而在攻击者拥有少量背景知识的前提下,这些方案仍存在隐私泄漏的的风险。
对此,MANNHARDT等[1]提出基于(ε,δ)差分隐私的隐私保护引擎,作为事件日志的唯一访问节点,过程挖掘算法只能利用受限的查询操作获取事件日志,该方法在理论上保证无论攻击者是否掌握背景知识,都不能识别个人信息;FAHRENKROG-PETERSEN等[12]提出隐私保护的事件日志发布(PRIvacy-Preserving Event Log publishing, PRIPEL)框架,该框架遵循本地化差分隐私原则,在案例级别而不是整个日志提供差分隐私保障;ELKOUMY等[9]针对差分隐私带来的效用损失提出基于效用损失估计差分隐私参数ε的优化方法,因为非结构化事件日志的差分隐私保护需要引入大量噪声,使误差不断累积,进而产生较高错误率,所以差分隐私不适合非结构化事件日志的隐私保护。
FAHRENKROG-PETERSEN等[8]提出基于t-闭合和前缀树的事件日志清理算法(PREfix-Tree based event log Sanitization for t-closeness, PRETSA),采用K-匿名和T-闭合作为隐私保护要求,对违反隐私保护要求的轨迹寻找相似轨迹并进行合并,直到达到隐私保护要求,该算法通过细粒度的转换保证了效用的适度损失,但是无法避免非频繁轨迹的丢失,而这些非频繁轨迹对过程挖掘至关重要;RAFIEI等[10]针对事件日志的高维稀疏性,从案例的视角提出一个TLKC隐私保护模型,并采用贪婪算法抑制事件获得匿名日志,该方法比PRETSA算法能够保留更多的轨迹变体,但是事件日志的匿名化过程容易陷入局部最优。针对TLKC隐私保护模型存在的问题,本文将事件日志匿名化问题转化为活动抑制集的种群进化问题,通过改进遗传算法、缩小可行解范围降低匿名事件日志的效用损失。
3 预备知识
为叙述方便,首先定义过程挖掘隐私保护相关的基本概念与表示符号。
给定一个活动集合A,σ∈A*为集合A上的一条活动轨迹。σ1σ2,σ1,σ2∈A*,表示σ1是σ2的子轨迹。σ′=(a1,t1),(a2,t2),…,(an,tn)表示简单轨迹,其中a1,a2,…,an∈A,t1,t2,…,tn∈T为事件的时间戳,∀(ai,ti)inσ′表示σ′中的一个活动时间对。|σ′|表示轨迹的长度,πk(η)=πk(x)|x∈η为投影到第k个属性上的投影序列,其中η是一个n元组,n≥k。
定义1带敏感属性的过程实例。P=C×(A×T)*×S为过程实例的域。c∈C为案例ID,s∈S为案例的敏感属性,σ′为案例的简单轨迹,P=(c,σ′,s)∈P表示一个带敏感属性的过程实例。
表2所示为由带敏感属性的过程实例表示的事件日志。

表2 一个简单事件日志

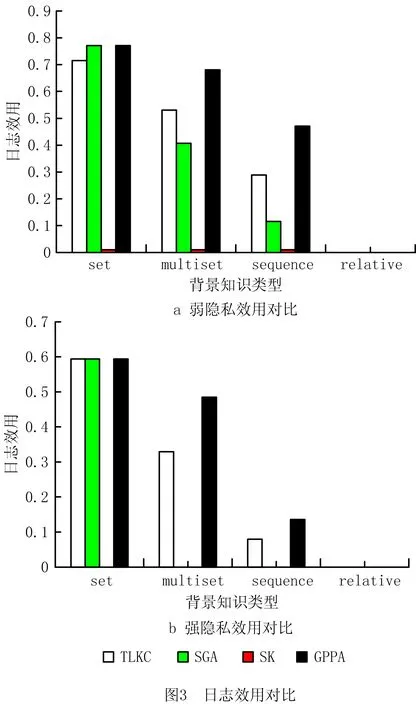
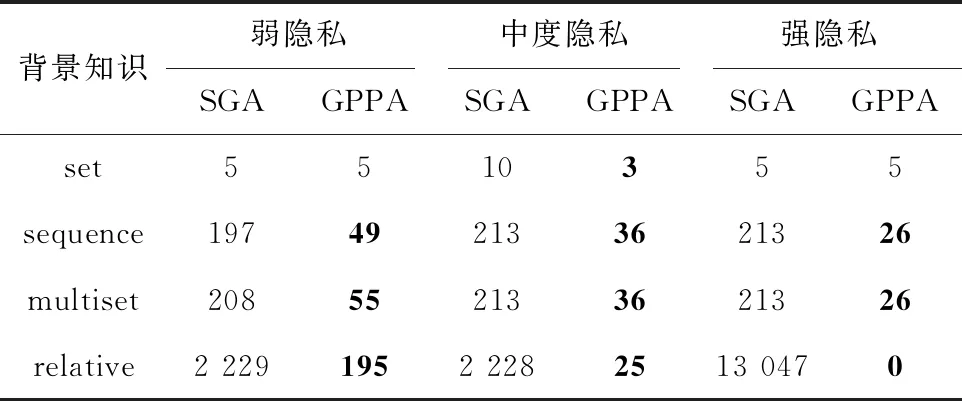
定义2TLKC隐私[10]。EL为一个事件日志,L为背景知识的最大长度,时间戳精度T∈{seconds,minutes,hours,days},背景知识的类型type∈{set,mult,seq,rel},EL(T)为时间戳精度为T的事件日志。EL(T)满足TLKC隐私,当且仅当∀σσ′,(c,σ′,s)∈EL,0<|σ|≤L满足且s∈S,0 定义3违规轨迹(Violating Trave, VT)[10]。EL为一个事件日志,σσ′,(c,σ′,s)∈EL,L为背景知识的最大长度,背景知识的类型type∈{set,mult,seq,rel}。如果或则σ是一个违反TLKC隐私的违规轨迹。 定义4最小违规轨迹(Minimal Violating Trace, MVT)[10]。EL为一个事件日志,违规轨迹σσ′,(c,σ′,s)∈EL,如果违规轨迹σ的任何子轨迹都不是事件日志EL的违规轨迹,则其为一个最小违规轨迹。 定义5最大频繁轨迹(Maximal Frequent Trace, MFT)[10]。EL为一个事件日志,给定最小支持度阈值Θ,一个非空轨迹σσ′,(c,σ′,s)∈EL。如果轨迹σ是频繁的,即σ出现的频率大于等于Θ,且σ的任意一个超集都不是频繁的,则σ是一个最大频繁轨迹。 遗传算法是一种基于自然选择和群体遗传机理的搜索算法,其模拟了遗传过程中的繁殖、杂交和突变现象[13]。基本遗传算法(Simple Genetic Algorithm, SGA)采用经典遗传算子——比例选择算子、单点交叉算子和基本位变异算子进行遗传[14]。因为事件日志数据具有高维稀疏的特点,所以SGA搜索TLKC隐私保护方案时往往无法得到高效用的数据集。 例如,表2的活动可以有不同长度的组合,每种组合都是一个候选的活动抑制集,但不是每个候选活动抑制集都是可行解,即满足隐私保护要求。在初始化阶段,可能得到全部个体均不可行的初始种群,导致直接应用SGA无法通过选择个体进行遗传。 即使随机生成的初始种群中有可行解,也不能避免在进化过程中再次出现种群大量个体不可行的情况。这是由于事件日志初始化的抑制集种群中可行解比较稀疏,导致选择后的种群有很多重复个体,种群多样性变差,即使选择的种群多样性好,使用基础遗传算子交叉变异后仍会产生大量不可行解,甚至出现整个种群都不可行的极端情况。 针对上述问题,本文提出一种遗传隐私保护算法。首先分析可行解的必要条件及约简规则,缩小遗传算法搜索空间,提高种群进化效率;然后基于日志相似性、轨迹变体和最大频繁轨迹集合设计适应度函数,引导种群向高效用进化;最后改进遗传算子与遗传过程,增加种群的多样性。 定义6活动抑制集。v_set={mvt1,mvt2,…,mvtn}为事件日志EL的最小违规轨迹集合,v_a={v|vinmvt⊂v_set}为v_set中所有活动构成的集合。supp_set∈2va为EL的一个活动抑制集,简称抑制集。 给定隐私要求T=hours,L=3,C=0.5,k=2,背景知识类型multiset,根据表2可得如表3所示的最小违规轨迹集合v_set,其活动抑制全集v_a={(m,1),(d,3),(r,2),(v,2),(r,3),(c,3),(b,1),(r,1),(e,1)(v,1),(d,2),(c,2)}。对∀v∈v_a,权重w(v)表示抑制包含v的活动后原日志轨迹变体的减少量,根据定义7可知一个可行活动抑制集能移除日志中所有MVT,使日志满足隐私要求,据此可以分析出可行抑制集的必要条件和约简规则。 表3 最小违规轨迹 证明假设∃mvt⊂v_set∧|mvt|=1,抑制集supp_set为可行解,且v∈mvt∧v∉supp_set,则通过抑制supp_set不可能移除最小违规轨迹mvt。匿名日志不可能达到TLKC隐私要求,与当前抑制集是可行解的假设条件矛盾。证毕。 例如表3中5号最小违规轨迹仅包含一个活动(r,3),只有抑制(r,3)才能消除5号最小违规轨迹,因此(r,3)一定在抑制集中。 定理2抑制集约简。∀v1,v2∈v_a,若f(v2)⊆f(v1),且w(v1)≤w(v2),则抑制集中v2可由v1替代。 证明因为抑制v1较抑制v2可以消除更多的mvt,而且损失的轨迹变体更少,所以v1可以完全替代v2在抑制集中的作用。 例如表3中的(e,1)和(r,1),抑制前者可以移除4条最小违规轨迹,抑制后者可以消除1条最小违规轨迹,且前者的权重等于后者的权重,因此活动(e,1)可以完全替代活动(r,1)。 定理3抑制集约简。∀v1,v2∈v_a,若f(v2)⊂f(v1),且w(v1)>w(v2),则两个活动互斥,即不同时存在于抑制集中。 证明因为f(v1v2)=max(f(v1),f(v2)),且w(v1v2)≥w(v1)>w(v2),即同时抑制v1,v2不会移除更多的MVT,但是可能改变更多的轨迹变体,损失更多的日志信息,所以v1,v2不应同时出现在抑制集中。 例如表3中的(e,1)和(v,1),两个活动不应该同时被抑制,其存在互斥关系。 大部分过程发现算法通过挖掘活动的常见关系模式(如直接跟随关系、互斥关系、并行关系)来构建业务过程模型。因此,根据过程模型相似性度量[15],给出基于日志次序关系的日志相似性度量公式,作为数据效用度量的一部分。 定义8基于日志的次序关系[16]。EL表示一个基于A的事件日志,令a,b∈A,则: (1)a>ELb(直接跟随关系),当且仅当存在一个轨迹σ=e1,e2,…,en,i∈{1,…,n-1},使得σ∈EL,ei=a,并且ei+1=b。 (2)a→ELb(因果关系),当且仅当a>ELb,b≯ELa。 (3)a#ELb(互斥关系),当且仅当a≯ELb,b≯ELa。 (4)a‖ELb(并行关系),当且仅当a>ELb,b>ELa。 给定事件日志EL和匿名日志EL′,EL→,EL#,EL‖分别为EL的因果关系、互斥关系、并行关系集合,匿名日志EL′也有同样的关系集合,通过这些集合计算日志的相似性。 w‖为并行关系的权重, (1) w#为互斥关系的权重, (2) w→为因果关系的权重, (3) 并行关系的相似性是用日志EL和EL′所有并行关系的交集元素数除以日志EL和EL′所有并行关系的并集元素数,即 (4) 对于互斥关系的相似性,用日志EL和EL′所有互斥关系的交集元素数除以日志EL和EL′所有互斥关系的并集元素数,即 (5) 对于因果关系的相似性,用日志EL和EL′所有因果关系的交集元素数除以日志EL和EL′所有因果关系的并集元素数,即 (6) 两个日志EL,EL′的相似性为并行关系的权重乘以并行关系的相似性、互斥关系的权重乘以互斥关系的相似性、因果关系的权重乘以因果关系的相似性这三者的累加和,即 sim(EL,EL′)=w‖×sim‖(EL,EL′)+ w#×sim#(EL,EL′)+w→×sim→(EL,EL′)。 (7) 基于活动抑制集和日志相似性,本文设计的遗传隐私保护算法(Genetic Privacy Preserving Algorithm, GPPA)分为初始化、个体评价和遗传操作3个阶段。图1所示为算法的工作流程。 步骤1初始化。随机生成规模为N的初始群体P0。初始化步骤持续至搜索到至少一个满足TLKC隐私的解为止,编码方式为multi-hot。 步骤3遗传操作。多点交叉随机生成交叉点会导致一些无意义的遗传操作或产生无用个体,例如交叉点处两个体基因型相同、交叉后未产生新个体或交叉产生的个体包含的活动数为0。为了减少这些无意义的操作并增加种群多样性,交叉算子采用改进的多点交叉机制。先确定每对父代个体基因型中基因不同的位置,在这些位置中生成多个交叉点,交叉点的个数应小于不同基因数的一半,以确保产生新的个体。如果基因型中的活动数小于1,则对个体使用变异算子,变异算子采用改进的单点变异和多点变异。若变异前,个体基因型中的活动数小于1,则随机生成一个其他活动,其余部分与经典的单点变异和多点变异相同。该步骤同时进行交叉与变异,每次迭代比较一对父个体的适应度值,以及多点交叉、单点变异和多点变异后子代个体的适应度值,选取适应度值最高的两个个体遗传到下一代,此处设计的最佳保留策略能够将每代的最优解保留在子代中,保证了遗传算法的收敛性,而交叉和变异算子混合使用的方式显著提高了种群多样性,避免了结果陷入局部最优。 步骤4终止条件判断。达到迭代次数后停止迭代,算法结束。 算法1基于遗传算法的隐私保护方法GPPA。 输入:原始的事件日志EL,L,K,C;敏感属性S;种群大小N;迭代次数NG;交叉率Pc;背景知识类型bk_type;频繁阈值ϑ。 输出:满足TLKC隐私的匿名事件日志EL′. 1.生成EL的最大频繁轨迹集f_set和最小违规轨迹集v_set 2.for each mvt⊂v_set do 3. if mvt满足定理1,then将v∈mvt加入抑制集sup_set,从v_set中移除mvt 5.根据v_set生成v_a 6.for each v⊂v_a do 7. if 活动v∈mvt满足定理2,then从v_a中移除v,从v_set中移除mvt 8.if 最小违规轨迹数全部移除,returnsup_set 9.else 根据v_a: 10. 随机生成种群大小为N的初始种群P0 11. for eachi∈P0 do 12. if i满足定理3 ,then对个体i使用罚函数 13. else 计算i的适应度值fit 14. while 迭代次数 15. 对P中个体进行交叉与变异,产生下一代大小为N的种群Q 16. P = Q 17. 计算P中个体的适应度最大值,对应的个体加入sup_set 18.for each v∈v_set do 19. 抑制事件日志所有实例中包含活动v的事件 20.return EL′ 为验证GPPA的有效性,从所得模型的误差和匿名日志有效信息的角度,将GPPA和TLKC算法与基线算法进行对比。其中,基线算法包括SGA和简单的K-匿名算法(Simple K-anonymity, SK),SK算法通过删除日志中所有出现次数少于k次的轨迹实现事件日志匿名;SGA在实验中不能保证得到可行解,因此对SGA进行少量修改以得到可比较的结果。首先,针对SGA不收敛的问题加入最佳保留策略,将每代的最优解保留到下一代,然后用GPPA中的初始种群生成策略搜索到可行解。基于4种背景知识、3种隐私强度,本文共进行了120组实验。 过程发现算法采用主流的inductive miner infrequent[17],以保证研究结果的普适性。实验采用的败血症病例日志[18](sepsiscases)是典型的卫生保健领域的医疗事件日志,存在许多罕见的变体,每个案例代表患者接受治疗的过程。该日志包括16个活动、1 050个实例、15 214个事件、846个变体,即80%的实例轨迹是唯一的;轨迹的最短长度为3,最大长度为185;最频繁的轨迹变体出现了35次,每种变体平均出现1.2次。 遗传隐私保护算法的参数调优结果如表4所示。表4确定了遗传算法的3个参数,即种群大小为50,迭代次数为200,频繁阈值和交叉率均为0.8。其余实验参数设置如下:敏感属性设置为“诊断”;置信值C的上限设置为0.5,即一个实例至少有两个不同的敏感值。实验设置了3种隐私强度,其中弱隐私参数为L=2,K=10,C=0.5,中度隐私参数为L=4,K=40,C=0.4,强隐私参数为L=6,K=80,C=0.3。适应度函数取法见4.3节。 表4 参数调优 图2所示为日志匿名后所得模型M′与原日志所得模型M的3个指标fitness,precision,F1-score[19]之间的平均绝对误差MAE的平均值。MAE表征M′与M的偏离程度,其值越大,M′与M的差别越大。从图2可见所提方法的3个指标与原模型的差别最小,原因在于GPPA采用改进遗传算子有效增加了种群的多样性,从而增强了算法的全局搜索能力,提高了解的质量。由120次实验结果分析可知,采用GPPA得到的M′与M的precision误差缩小3%~7%,原因是新方法着眼于保留日志的次序关系,而模型precision[20]的计算与日志中的直接跟随关系强相关,因此包含基于日志的次序关系的适应度函数可以搜索到精度更高的结果。另外,4个方法中SK方法的误差最大,原因是该方法删除了大量轨迹变体,使得强隐私下的整个日志都被删空,日志信息损失较多。 图3所示为GPPA与对比方法在日志数据效用(见4.2节)保留方面的对比结果,图4所示为日志剩余轨迹变体数量的对比结果。可见,TLKC,SGA,GPPA 3个使用TLKC隐私要求的方法在set背景知识下的结果非常相似,均高于使用K-匿名隐私模型的SK方法,原因是这3种方法只需抑制少量活动即可抵御具有弱背景知识的隐私攻击,而SK方法需要抑制的是整条轨迹,因此数据效用损失更大。在multiset和sequence这样较强的背景知识下,GPPA明显较对比算法保留了更多的数据效用和轨迹变体,原因是TLKC方法仅考虑活动出现在频繁轨迹中的次数这一因素,无法精确区分不同活动的效用,GPPA则在此基础上加入基于日志的次序关系和轨迹变体数量共同引导种群进化,容易搜索到高数据效用的解。3种方法在relative这种强背景知识下的数据效用均较低,这是容易理解的,因为攻击者掌握了时间这样精确的信息,所以进行隐私保护就需要付出更大的代价。 由图3和图4可见,SK方法在数据效用和轨迹变体数量上获得的结果均最差,原因是该方法采用简单粗暴的方式对日志进行粗粒度转换,删除了大量日志轨迹。值得注意的是,SK方法采用K-匿名隐私模型,不考虑攻击者是否掌握时间戳和敏感属性的概率信息,无法抵御链接攻击,在relative这样强的背景知识下,不能提供所需的隐私保护,相比使用TLKC隐私模型的3种方法,只能提供较弱的隐私保障。日志效用和轨迹变体两组对比实验结果显示,GPPA生成的事件日志保留了更多的轨迹变体和基于日志的次序关系,表明所设计的适应度函数具有较强的筛选能力。 表5所示为两种遗传算法方案SGA和GPPA空间规模的对数值(log2)对比。可见,GPPA的方案空间较未使用定理的SGA的方案空间有大幅缩减,relative背景知识下的缩减最明显,原因是relative背景知识会产生大量长度为1的最小违规轨迹,利用定理1可显著缩小方案空间规模。 表5 两种遗传算法方案空间规模的对数值(log2)对比 本文提出一种基于遗传算法的过程挖掘匿名化算法,将过程挖掘的隐私保护与效用权衡问题规约为活动抑制集优化问题,并通过研究活动抑制集可行性的必要条件和约简定理,显著压缩了抑制集求解空间。根据主流过程发现算法的共性,设计了综合效用函数引导遗传算法的进化过程,并采用最佳个体保留策略加速算法收敛。最后在真实的事件日志上与TLKC和基线算法进行了对比实验,实验结果表明,该方法得到的模型精度误差比TLKC算法缩小3%~7%。未来将研究更高效的优化算法,以进一步提高匿名化事件日志的可用性。4 基于遗传算法的隐私保护方法
4.1 活动抑制集

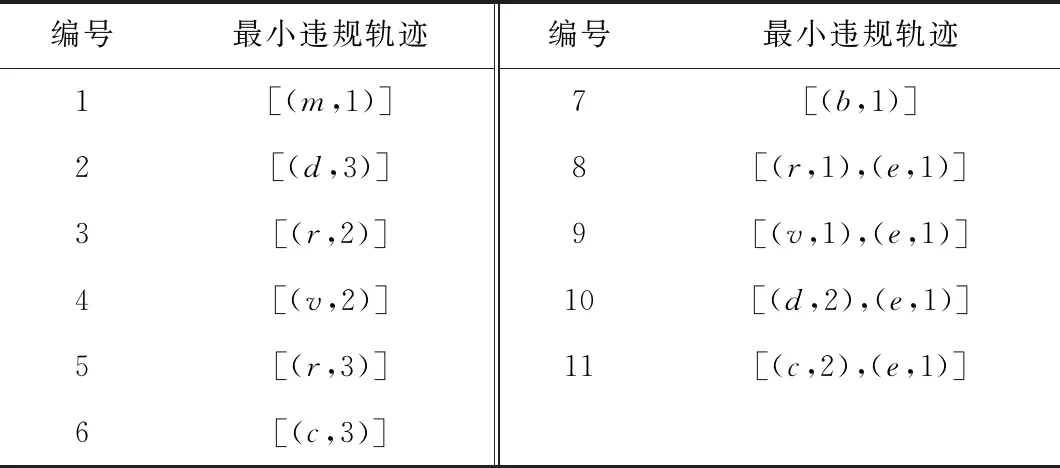
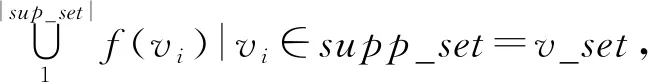
4.2 日志相似性度量
4.3 遗传隐私保护算法
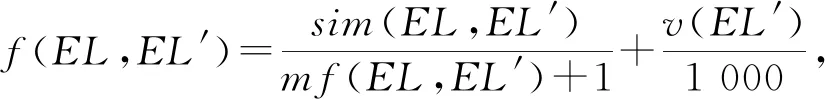

5 实验设计与分析
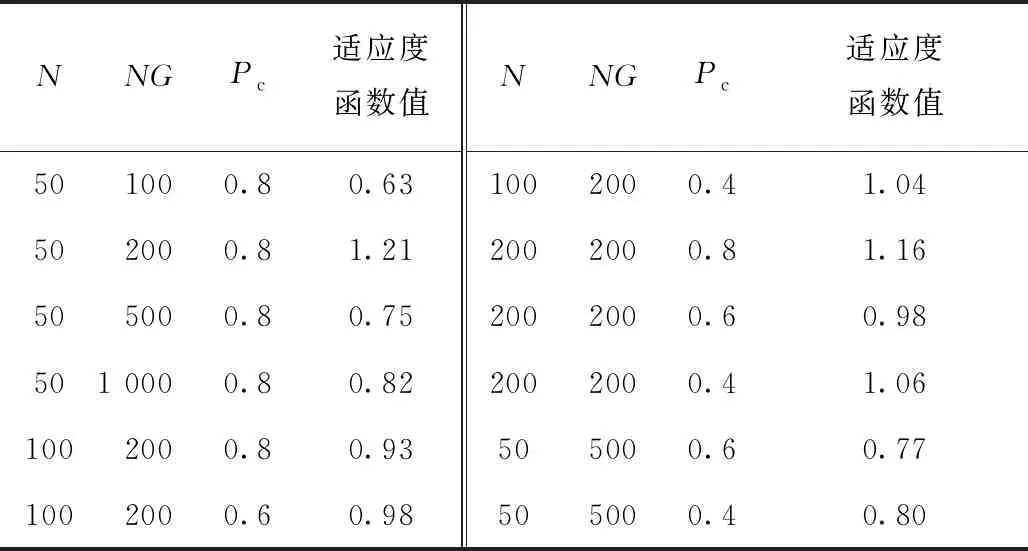
5.1 实验参数设置
5.2 模型误差实验分析

5.3 日志信息实验分析

6 结束语
