基于在线模型的业务过程剩余时间预测

高俊涛,陈 珂,刘云峰,刘 聪

(1.东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318；2.山东理工大学 计算机科学与技术学院，山东 淄博 255000)

1 问题的提出

作为业务过程管理领域一个新兴的研究方向，预测性监控(predictive monitoring)可以通过对处于运行阶段的业务过程进行性能预测及调控，将传统过程管理的事后补救模式转变为主动的事前预防模式，帮助企业积极应对业务风险，提高业务过程的敏捷性和高效性。预测性监控的对象包括过程的运行时间、成本、服务质量和风险等多项性能指标，其中运行时间作为业务过程管理的核心内容，是企业进行计划、监控、绩效评价的基础，及时准确地提供业务过程的剩余运行时间不仅有助于业务过程优化，还可以提高顾客满意度。

现有方法主要采用离线模型预测业务过程的剩余时间，如图1a所示。预测模型采用离线方式构建，并利用数据挖掘或机器学习技术分析历史事件日志，抽取或训练预测模型，例如VAN DER AALST等[1]提出的基于变迁系统(Transition System, TS)的预测方法和TAX等[2]提出的基于长短期记忆(Long Short Term Memory, LSTM)的预测方法。随着物联网及大数据技术的迅猛发展，时刻都有新的事件数据以前所未有的速度产生，如机场的行李处理事件、晶片制造事件[3]，这种流式事件日志给传统的预测方法提出了巨大的挑战，使得传统的离线模型构建周期长、更新成本高、内存消耗大的问题在应对流式事件日志中更加突出。一方面，流式事件日志增长快、体量大，传统预测方法每次更新模型需要将原有模型推倒重建，计算成本越来越高；另一方面，较长的更新周期会使预测模型滞后于当前的业务系统，模型性能容易出现老化现象，影响预测的准确性[4]。针对流式事件日志，研究实时的剩余时间预测方法不但能及时利用新产生的轨迹数据，使预测结果更加符合业务现状，而且可以降低预测算法的时间和空间复杂度。

本文采用在线模型预测模式，提出一种实时的业务过程剩余时间预测方法(如图1b)，根据新完成的轨迹数据实时更新预测模型。为保证预测模型的实时性，本文在带标注变迁系统的基础上提出增量式模型构建算法，并针对传统变迁系统类方法缺少抽象机制的选择策略问题，定义预测信度的评价指标，通过对变迁系统多种抽象机制的融合提高剩余时间预测的准确性。

本文的主要贡献如下：

(1)通过简化变迁系统状态的标注方式，有效缓解变迁系统模型规模随样本数据积累过度增长的问题，同时采用增量式模型构建算法，保证预测模型实时感知业务系统的变化。

(2)定义波动性指标来衡量预测结果随时间推移调整的幅度，完善预测结果评价指标体系，通过持续稳定的预测结果增强终端用户对预测模型的信任。

(3)定义预测信度融合传统变迁系统的多种抽象机制，提高剩余时间的预测准确性，通过引入回顾机制进一步提高准确性并降低波动性。

2 研究现状

现有剩余时间预测方法主要分为基于活动的预测和基于案例的预测两类。基于活动的预测通常在业务过程模型基础上对活动的持续时间进行建模，然后根据活动间的逻辑关系推算整个过程的剩余时间；基于案例的预测不考虑过程内部的执行逻辑，通过比对以往类似的案例，直接在案例级别分析剩余时间的影响因素和变化规律，其通常将预测任务转化为数据挖掘问题，然后采用经典的数据挖掘或机器学习算法建立预测模型，这类方法可以规避活动间相互影响带来的预测复杂性。

(1)基于活动的预测方法

基于活动进行预测的代表性方法包括ROGGE-SOLTI等[5-6]提出的基于随机Petri网的预测方法和VERENICH等[7-8]提出的基于流分析(flow analysis)技术的预测方法。随机Petri网包括每个活动执行时间的概率分布，在此基础上预测后续活动执行的剩余时间；流分析技术通过分析各种控制结构下活动执行时间的分解组合关系，定义过程执行时间的数学模型。基于活动的预测方法采用直观的过程模型作为预测模型架构，其推理过程易于理解，预测模型可解释性强，然而该方法目前大多基于活动间持续时间相互独立的假设，该假设在很多实际应用场景并不成立。2017年，TAX等[2]将循环神经网络引入剩余时间预测问题，通过LSTM预测业务过程的后续活动和活动持续时间，并在二者基础上估算过程的剩余执行时间。该方法不需要构建业务过程模型，为基于活动的预测研究提供了新的思路。

(2)基于案例的预测方法

基于案例的预测方法借助包括SVM[9-10]、决策树[11-12]、聚类[13-14]和回归分析[15]在内的多种数据挖掘模型和算法分析影响监控指标的企业过程因素和外部环境因素。VAN DER AALST等[1]提出TS预测方法，该方法用变迁系统描述过程实例所有可能的状态，并在每个状态上标注时间信息，以便根据当前过程实例所处的状态预测其剩余执行时间；FOLINO等[16]提出CA-PPM(context-aware performance prediction model)模型，在TS系统基础上增加了过程实例聚类环节，为每过程实例簇定义了不同的TS预测模型；BEVACQUA等[17]提出AA-TP(adaptive-abstraction time prediction)方法，通过挖掘事件日志中的频繁项集自适应地构建结构模式，使过程实例聚类更加智能化;BEVACQUA等[18]对该方法进一步扩展，提出AA-PPM框架，支持在适合的抽象层次上分析日志；随后，POLATO等[19-20]提出数据感知的TS系统，采用朴素贝叶斯分类器和支持向量回归分析方法进行预测；VERENICH等[21]用过程树作为作为预测模型，在过程树的活动节点和网关节点上分别训练回归方法和分类方法来预测剩余时间；倪维健等[22]将基于注意力的双向循环神经网络模型应用于过程剩余时间预测问题，取得了较好的实验效果。这类方法采用事件日志作为基本输入条件，企业不需要提供额外的业务数据，不仅广泛应用于业务过程管理领域，还可用于预测制造过程的产品周转时间[4]。

目前，基于深度学习的预测方法虽然准确性较好，但是预测模型的可解释性较差[22]，在一定程度上影响了用户对预测结果的信任度[23]。还有一些基于深度学习的预测方法引入了事件最小属性以外的变量[20,24]。因为每类事件日志提供的属性变量不同，所以需要采用专门的编码方式。

本文采用包含最小属性集合的标准事件模型作为预测模型构建的样本数据，以保证预测方法的普适性。针对现有预测模型普遍存在的构建周期长的问题，该方法采用增量式模型构建算法，使预测模型及时反映业务系统的最新动态；同时基于在线预测模型引入回顾机制，以提高预测的准确性，降低预测结果的波动性。

3 预备知识

3.1 基本概念

为了方便叙述，首先对业务过程剩余时间预测的相关概念及表示符号进行定义和说明。

定义1事件。事件e是构成业务过程的基本元素，具有瞬时性，可以用三元组(cid,act,time)描述。其中cid为事件所属过程实例的内部标识，act为产生事件的活动，time为事件发生的时间。

定义1描述了事件的最小属性模型，缺少任何元素都无法开展过程挖掘工作。虽然实际事件日志可能包含更多的事件属性，如资源、设备、场地等，但是为保证研究结果的普适性，本文仅采用事件最小属性模型分析剩余时间的预测方法。

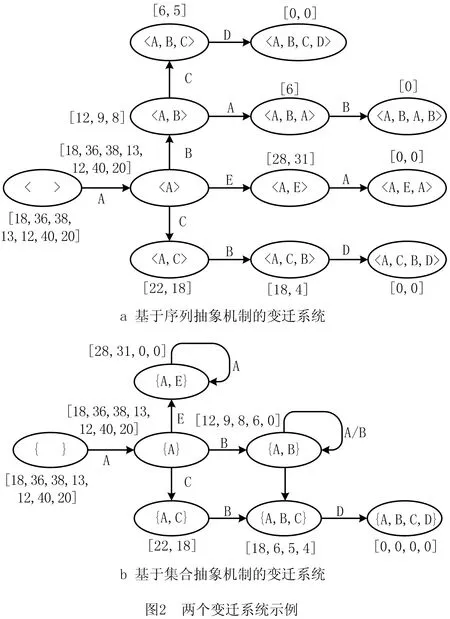
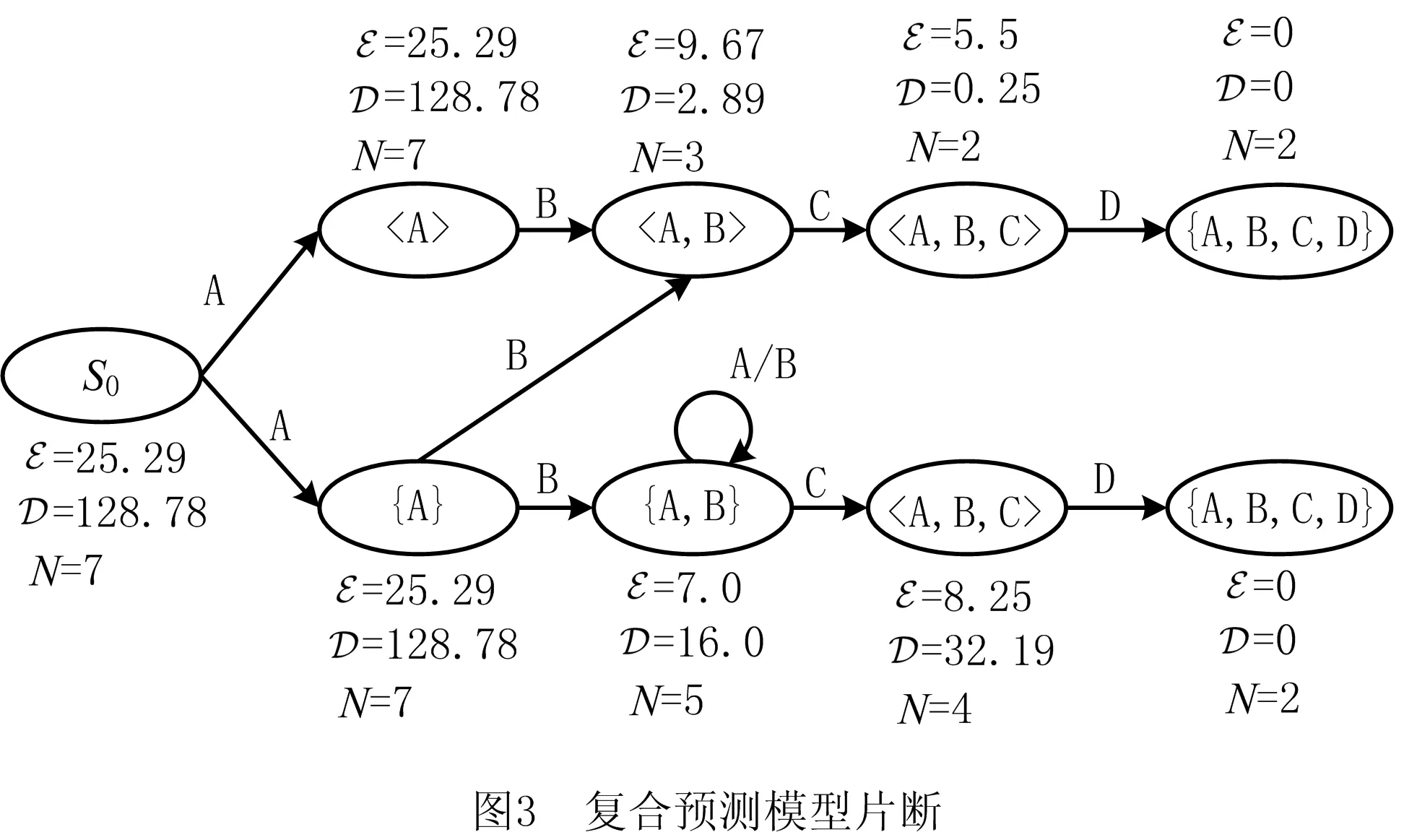
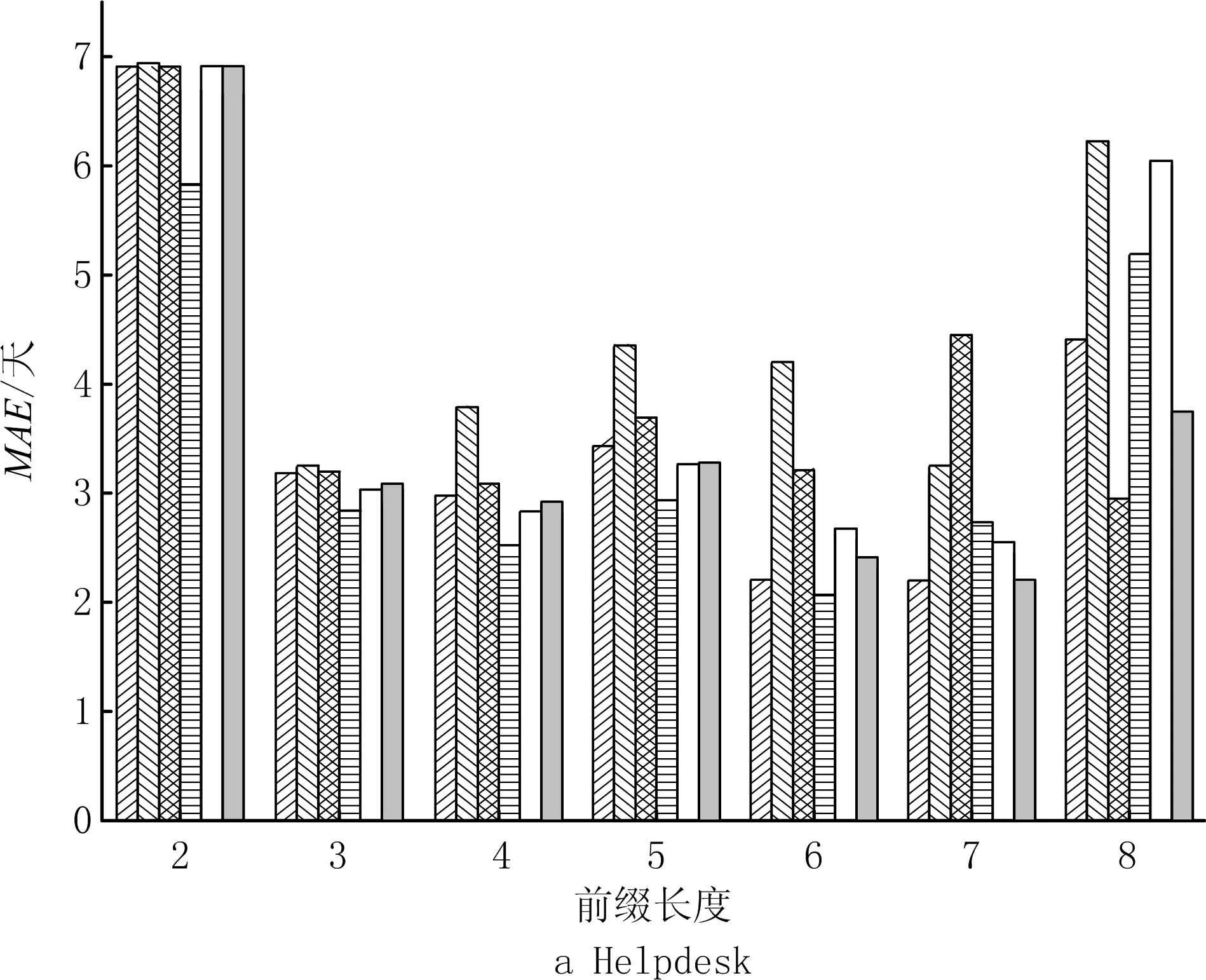
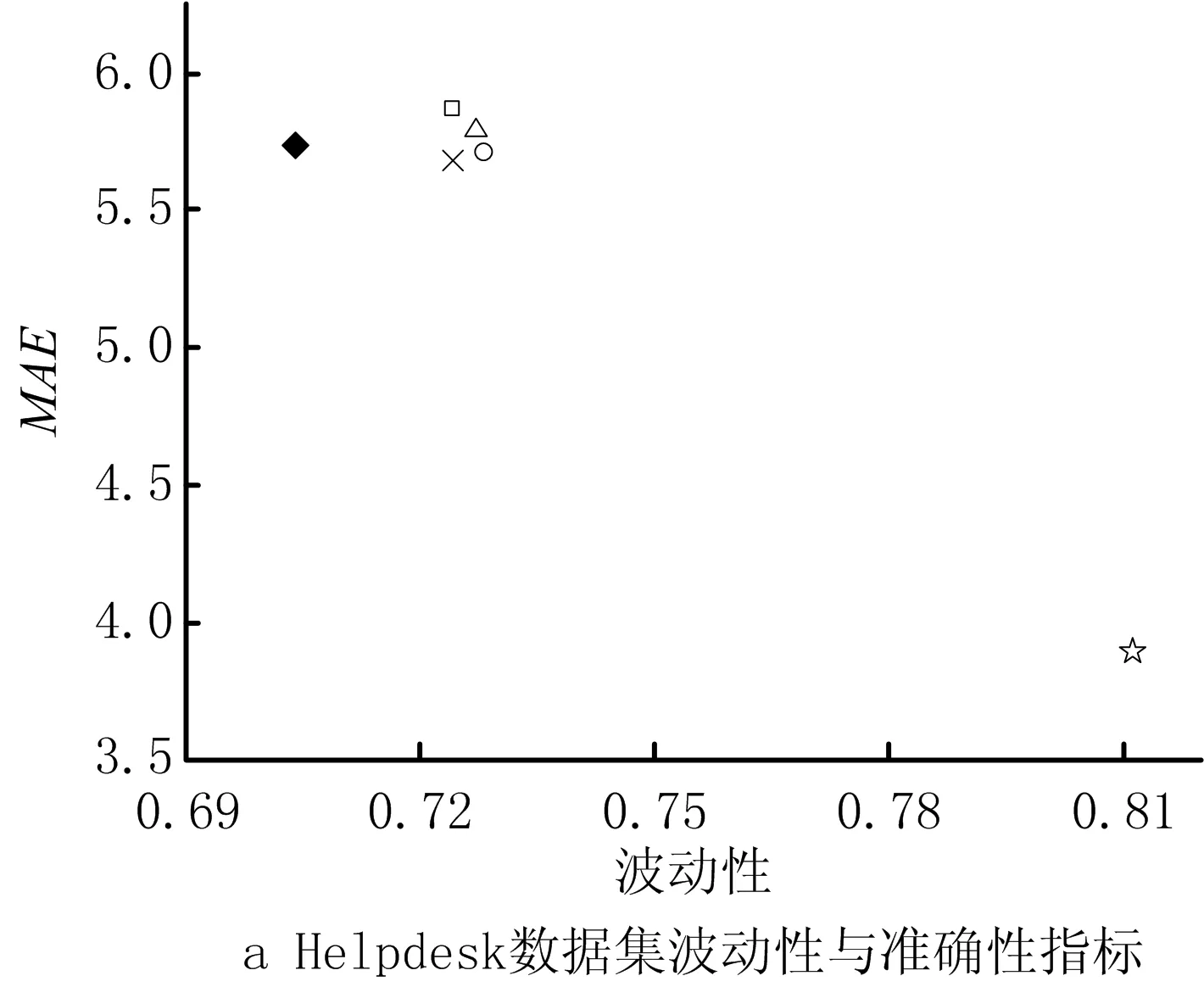
定义2轨迹。轨迹σ=e1,…,em用于记录业务过程所产生的事件，是一个有限非空的事件序列，且∀i,j∈[1,m],ei.cid=ej.cid。若1≤i

函数spanσ:N×N→R计算轨迹中两个事件发生的时间间隔，即ei.time-ej.time。若ei比ej发生得早，则spanσ(i,j)的结果为正数，反之为负数。

定义3轨迹前缀。轨迹前缀hdk(σ)通过截取轨迹σ的前k个事件得到，即e1,…,ek(k∈[0,|σ|])，对于任意轨迹σ，hd0(σ)=φ。

假设轨迹σ是某业务过程完成时留下的完整运行轨迹，其前缀hdk(σ)的剩余时间由函数ret(hdk(σ))计算，即该轨迹前缀距离整个业务过程结束所需的时间为spanσ(k,|σ|)。

显然，运行态业务过程尚未结束，其剩余时间是未知的。剩余时间预测的目标是根据当前过程已经产生的部分轨迹δ，预测整个过程完成所需的剩余时间。剩余时间预测通常包括构建预测模型和预测过程实例两个阶段。业务系统运行产生的历史事件是构建预测模型的基础，通常以事件日志的形式保存。

定义4事件日志。事件日志L={σ1,…,σn}是轨迹的集合，用于记录业务过程执行中已经发生的历史事件，每个事件在整个日志中最多只出现一次。

3.2 变迁系统

变迁系统(transition systems)从状态的观点描述业务系统的行为，是过程挖掘的基本概念。

定义5变迁系统。变迁系统是一个三元组TS=(S,,T)，其中S为状态集合，为活动集合，T∈S×A×S为转移集合。

VAN DER AALST提出的TS预测方法采用带标注变迁系统预测业务过程剩余时间。TS方法允许采用序列、多重集、集合等多种轨迹抽象机制构建状态，并基于状态预测剩余时间。TS预测模型比较直观，具有内生可解释性，但未说明如何选择抽象机制，选择不同的抽象机制会导致预测时间产生较大的差异。

根据表1所示的轨迹数据，采用序列抽象和集合抽象分别学习得到图2所示的两个模型，对轨迹前缀A,B,C预测剩余时间。采用序列抽象的预测值为图2a所示的变迁系统状态S〈A,B,C〉上所标注样本数据[6,5]的均值5.5，采用集合抽象的预测值为图2b所示变迁系统状态S〈A,B,C〉上所标注样本数据[18,6,5,4]的均值8.25。表1中轨迹5和轨迹6均包含前缀A,B,C，剩余时间的真实值应为结束事件D的发生时间减去事件C的发生时间，分别为5和6。因此序列抽象预测结果的平均绝对误差MAE=(|5-5.5|+|6-5.5|)/2=0.5，集合抽象预测结果的MAE=(|5-8.25|+|6-8.25|)/2=2.75。

表1 轨迹数据例子

4 复合变迁系统

本文融合多种抽象机制，将TS预测方法采用的只包含单一抽象机制的确定性变迁系统扩展为包含多种抽象状态的不确定性复合变迁系统，以提高预测模型的表达能力，同时定义预测信度应对模型不确定性给预测带来的困难。因为复合变迁系统包括序列、多重集和集合3种抽象状态，所以模型包含的信息更丰富，规模也更庞大。TS预测方法将剩余时间观察值直接标注在状态上，每个状态上可能被标注几百甚至上千条数据，随着历史轨迹数据的积累，样本规模持续不断地增长，该问题在复合变迁系统中变得更加突出。本文采用样本统计量[1](如样本均值或方差)标注状态，并研究相应的模型更新算法。定义6给出复合预测模型的形式化定义。

定义6预测模型。预测模型M是一个三元组M=(S,,T)，其中S为状态集合，为活动集合，T∈S××S为转移集合。状态S有4个属性：编码表示状态在变迁系统中的唯一标识；均值、方差、规模N分别表示状态所包含的剩余时间观察值的均值、方差和数量。

状态编码可以由轨迹经过序列、多重集和集合3种抽象得到。将表1所示的日志进行抽象得到复合预测模型片断，如图3所示。轨迹前缀A,B,C匹配的状态有〈A,B,C〉和{A,B,C}两个，对应的剩余时间期望值分别为5.5和8.25。

该模型的构建过程如下：初始预测模型只包含一个状态S0=(φ,0,0,N0)，描述历史事件日志L的全部采样数据，其中：φ为活动空集的编码；0，0，N0分别为日志L中所有轨迹周转时间的均值、方差和轨迹数。当有新业务过程完成并形成轨迹数据σ时，首先给σ的每个前缀标注真实剩余时间ret(hdk(σ))(k∈(0,|σ|))，然后调用函数update(M,σ)更新预测模型，该函数以增量方式更新样本的统计值，包括均值、方差和规模N。算法1描述了预测模型的更新过程，其中：函数set(σ)将序列σ转换为活动的集合，set(φ)=φ；函数bag(σ)将序列σ转换为活动的多重集，bag(φ)=φ;和′为某种抽象状态的编码。

算法1预测模型更新算法。

输入：原预测模型M=(S,,T)、轨迹σ。

输出：新预测模型M。

Function update(M,σ)

1 For i=0;i≤|σ|;i++

3. If{s|s∈S∧sC=}≠∅

4. Foreach m in{s|s∈S∧sC=}

8. Else

12. Foreach m′ in{s′|s′∈S∧sC=′}

14. return M

End Function

5 基于信度的预测算法

本章在复合变迁系统基础上，已知当前业务过程部分轨迹的情况下，介绍其剩余时间的预测算法。如算法2所示，剩余时间预测算法引入轨迹回顾机制扩大剩余时间的候选值集合，然后根据信度函数筛选出最可信的预测值。

(1)状态选择

复合变迁系统允许包含多种抽象机制，是一种不确定性的状态机。因此，将当前运行轨迹δ与预测模型M中的状态进行匹配，将每个匹配状态的样本均值作为预测值，得到包含多个剩余时间的候选值集合。常用的准确性评价指标包括平均绝对误差MAE、均方根误差RMSE或平均绝对比例误差MAPE等，TEINEMAA等[25]研究发现仅考虑预测结果的准确性是不够的，过程管理所做的决策必须基于高可信的预测结果，缺少信度的预测结果难以满足过程监控的实际需求。因此，本文定义信度函数conf:State→[0,1]评价预测值的可信度，以消除复合变迁系统的不确定性。

算法2剩余时间预测算法。

输入：预测模型M=(S,,T)、前缀轨迹δ。

Functionpredict(M,δ)

1.k=|δ|

2.maxconf=0 //最大信度

3. while(k>0)

5. Foreach m in{s|s∈S∧sc=}

6. If conf(m)>maxconf

8.maxconf←conf(m)

9.k←k-1

End Function

每个状态定义了一个描述剩余时间的随机变量，将随机变量的数学期望作为预测值，其信度可由该随机变量总体分布的方差定义。在得到有限的剩余时间观测值的情况下计算预测信度

conf(s)=a×logbsN-sD。

(1)

式中参数a和b可以根据事件日志包含的轨迹数量和剩余时间采用的度量单位进行调节。式(1)采用样本方差作为预测信度的反向指标，利用对数函数拟合样本规模与总体方差估算偏差间的关联关系。

(2)回顾机制

如果当前运行轨迹δ在预测模型M中找不到匹配的状态，则可先回顾轨迹前缀hd|δ|-1(δ)的剩余时间预测值，再推算当前轨迹δ的剩余时间，即predict(M,hd|δ|-1(δ))-(e|δ|·time-e|δ|-1·time)。其中predict(M,hd|δ|-1(δ))为轨迹前缀hd|δ|-1(δ)的剩余时间预测值，e|δ|-e|δ|-1为从上个事件发生到当前事件发生经过的时间。如果hd|δ|-1(δ)在预测模型中仍然找不到匹配的状态，则继续回顾hd|δ|-2(δ)，以此类推，直到找到存在匹配状态的轨迹前缀。在最极端的情况下，轨迹δ的首个事件就是由某个新活动产生的，在预测模型中不存在匹配状态，此时将根据初始状态S0进行预测。

实际上，即使当前轨迹δ存在匹配状态，回顾轨迹前缀也可能得到信度更高的预测值。在变迁系统的3种基本抽象机制中，序列抽象状态所包含的样本MAE最容易呈现单调性，尽管如此，随着时间的推进，很多过程实例匹配状态的剩余时间采样值会更加发散[1]。因此，无论能否直接从预测模型中找到匹配的状态，引入回顾机制都有可能提高预测结果的质量。

6 波动性

预测任务通常采用准确性进行评价，然而在实际应用场景中，只采用统计意义上的准确性不能全面反映用户对预测结果的要求。当对流程实例的剩余执行时间进行持续性预测时，每项预测任务在不同时间点可能得到多个预测结果，这种预测结果随时间调整的现象称为预测的波动性，波动性大的预测很难得到信任，因为终端用户不能判断哪个结果更准确[25]。

下面给出剩余时间预测的波动性计算方法。假设持续预测轨迹前缀δ=hdk(σ)的剩余时间，得到预测结果序列rs(δ)=ret(δ)，ret(hdk-1(δ))-spanδ(k-1,k),…,ret(hd1(δ))-spanδ(1,k)。每个元素用rsi(δ)表示，i∈[1,k]。为了消除剩余时间预测值的绝对值给波动性度量带来的影响，采用式(2)对rs(δ)中的每个元素进行归一化处理：

(2)

持续预测某个预测任务，即预测某条轨迹前缀δ的剩余时间，计算其波动性

(3)

计算轨迹σ包含的所有预测任务的波动性平均值

(4)

在整个日志L上所有预测任务的波动性平均值

(5)

7 实验设计与分析

7.1 实验设置

本文采用准确性和波动性评价预测算法的优劣。实验采用5个公开的事件日志数据集Helpdesk，bpi12_w，bpi12_w_no_repeat，Inovice，Environmental permit，如表2所示。

表2 事件日志统计信息

实验将日志切分为两部分，第1部分包括前2/3轨迹，作为训练集，剩余1/3轨迹作为第2部分测试集。采用训练集数据构建预测模型M，测试集数据检验预测方法的准确性。在线预测模型可以根据完成的轨迹数据及时更新，因此在实验测试阶段模拟了用刚完成的轨迹数据动态更新预测模型的过程。模拟实验采用过程池存放运行态过程实例，模拟时间步长设为step。每个时间步长内执行以下操作：

(1)根据日志中记录的事件发生时间，将该时间步长内已启动的过程实例加入过程池。

(2)为过程池中每个过程实例添加新产生的事件，将相应的轨迹hdk(σ)转变为hdk+j(σ)，其中j≥0，σk+1，…，σk+j为该时间步长内新产生的事件。

(3)记录从hdk+1(σ)到hdk+j(σ)的剩余时间预测值与真实值的偏离值。

(4)若k+j=|σ|，则将该过程实例置为完成态，调用update(M,σ)更新预测模型M。

(5)返回(1)模拟下一个时间步长的执行过程，直到测试集中所有轨迹都已创建过程实例，且处于完成态。

7.2 实验结果

7.2.1 准确性评价

实验采用MAE作为准确性评价指标，令信度函数的参数a=1，b=10。LSTM采用文献[2]给出的参数设置，其中学习率设为{0.01，0.1}，优化方法采用Nadam(nesterov-accelerated adaptive moment estimation)，迭代次数定为100轮，学习率调整倍数为[0.1，0.5]。为了独立检验信度和回顾机制的效果，基于信度的基本预测方法(简称基本信度方法)去除了轨迹回顾机制，而带回顾机制的预测方法(简称回顾信度方法)则完整实现了算法2的预测算法。

根据图4所示的实验结果可以得出如下结论：

(1)本文方法在绝大多数情况下优于传统TS方法和LSTM方法。与传统TS方法相比，基于信度的预测结果在过程运行早期并未表现出明显优势，这是由于过程运行早期产生的轨迹数据较少，所有抽象机制的预测准确性均较差。在过程运行中后期，基于信度的预测方法拥有更大的候选空间，预测准确性明显改善。这说明候选值充足时，信度函数能够有效识别优质预测结果。

(2)在大多数情况下，回顾信度方法的表现超过基本信度方法，说明轨迹回顾机制确实为预测算法扩充了优秀的候选值，进而改善了预测结果的准确性。

(3)虽然Helpdesk日志中LSTM方法的准确性优于本文方法，但是其预测模型的可解释性较差，而变迁系统具有内生可解释性，其预测结果可以通过展示历史轨迹的运行过程来解释，而且随着历史轨迹库积累数据的增多，更新LSTM模型需要昂贵的计算成本和较长的时间周期。本文采用的复合变迁系统的标签信息采用统计变量，不会因历史轨迹的增多而显著增长。而且，增量式模型构建方式大幅缩短了预测模型的更新周期，使得该方法在银行事务处理、电子晶片制造等流式事件日志处理等应用场景中的优势更加明显。

7.2.2 波动性评价

下面在整个日志集上比较基本信度方法、回顾信度方法与传统方法的波动性。由图5可见，在实验采用的5个数据集上，传统变迁系统的Sequence抽象虽然在Invoice数据集上的波动性比基本信度方法更小，但是基本信度方法不但突破了传统变迁系统抽象选择的局限性，而且提高了准确性；回顾信度方法在所有实验数据集上表现得比其他方法更加稳定，可见回顾机制在剩余时间预测中具有平滑效应，弱化了新产生事件给预测结果带来的波动。

由图6可见，传统变迁系统和LSTM模型很难兼顾预测准确性和波动性，因此距离坐标系统原点较远。回顾信度方法在bpi12_w，Invoice， Environment permit数据集上表现优异，其既给出较准确的预测，又表现出较低的波动性。这是因为回顾机制不仅为剩余时间预测增强了候选集，还能平滑不同时间点预测结果的波动幅度。基本信度和回顾信度方法在Helpdesk数据集上的准确性不如LSTM模型，主要原因在于复合变迁系统只包括序列、多重集、集合3种抽象状态，模型的表达能力比LSTM模型弱，以后可以通过增加对最大感受野和过滤器等抽象机制的支持来增强复合变迁系统的表达能力。

8 结束语

本文提出一种业务过程剩余时间的在线预测方法，改变了传统预测方法将模型构建与剩余时间预测截然分开的工作模式，设计了增量式模型构建算法来提高模型构建效率，使预测模型能够及时反映当前系统运行规律，定义了预测信度融合多种抽象机制的预测结果，并结合轨迹回顾机制增强预测候选集合。在5个公开事件日志上进行对比实验，结果显示该预测方法不仅改善了预测准确性，还降低了预测结果的波动性，提高了预测模型的可信度。目前，该方法只支持序列、多重集、集合3种抽象机制，未来可以通过增加对最大感受野和过滤器抽象机制的支持进一步提高预测效果。