用于流程发现的局部日志采样方法
2022-11-07俞东进孙笑笑
倪 可,俞东进+,孙笑笑,胡 华
(1.杭州电子科技大学 计算机学院,浙江 杭州 310018;2.杭州师范大学,浙江 杭州 311121)
0 引言
流程挖掘旨在从企业组织的信息管理系统中提取业务流程相关见解,其核心理念为发现、监测和改进真实的业务流程[1]。流程发现是流程挖掘的一个分支领域,其主要任务是从事件日志中构建流程模型,达到更好地理解和分析业务流程的目的。
事件日志是提取流程模型的基础。近年来,随着物联网、大数据等技术的快速发展,企业有了更多获取和存储事件日志的手段,使事件日志的规模呈几何级别增长。现有的流程发现算法,如Alpha挖掘算法[2]、启发式流程挖掘算法[3]、归纳算法[4]等,将完整的事件日志作为输入构建相应的流程模型,然而这些流程挖掘算法往往有多个可调整的参数,从而使流程发现成为一个漫长的探索性过程,尤其在将其应用于大规模事件日志时,可能需要较长的处理时间,导致流程发现效率低下。
为了应对大规模的事件日志,常采用分而治之的思想,将流程发现问题分解为若干个规模较小的子问题[5];另一种做法则是利用分布式计算提高流程发现的效率,例如EVERMANN[6]在MapReduce平台上复现并扩展了Alpha挖掘算法和启发式流程挖掘算法,使这两种著名的流程挖掘算法得以扩展应用到大规模、分布式存储数据集上。
除了改进现有挖掘算法,对完整的事件日志进行采样则是一种从根本上提高流程发现效率的方法[7]。这种做法的依据是,事件日志中存在大量相似或重复的行为,只有一小部分日志记录了导致流程模型发生变动的“新信息”。因此,将大规模的事件日志通过采样缩减到可快速处理的大小是一种十分有效的方式。
综上所述,本文的研究目标是从完整的事件日志中得到一个规模较小且信息损失较少的日志子集(文中称为采样日志)用于流程发现,主要解决3个问题:①从完整事件日志中提取控制流信息;②衡量采样日志的质量;③在事件日志存在大量重复轨迹的情况下避免遍历重复轨迹。
因此,本文提出一种适用于流程发现的、基于轨迹信息增量的局部日志采样方法,该方法从控制流和特征属性两个角度对轨迹所包含的信息进行量化,通过比较一条轨迹和已采样日志之间的信息差异来判断该轨迹是否记录了新的流程行为。特别地,由于现有的日志采样方法大都需要对完整的事件日志进行至少一次遍历,为了进一步提高采样速度,本文基于统计理论确定了最小连续遍历样本数,并提出二进制指数跳跃算法来处理相似轨迹聚集问题,其核心思想是避免完整扫描事件日志,即对局部日志进行采样。
1 相关工作
作为流程发现算法的输入,事件日志的质量也会影响流程发现的性能和结果,因此事件日志预处理逐渐得到研究人员的关注。为了发现更高质量的流程模型,一种做法是在应用流程发现算法之前对事件日志进行分析处理,以删除或修改事件日志中的离群值行为[8-10];另一种做法是直接在流程发现算法中内置噪声过滤机制,如Split Miner[11],ILP Miner[12]等。上述过滤技术专注于从事件日志中删除不频繁或异常行为,然而过滤低频率行为对事件日志总体数量的影响很小,对于大规模事件日志,流程发现所需的处理时间仍然很长。
为了提高流程发现算法的运行速度,一种有效的做法是对大规模事件日志进行抽样,这种方法既可以减少业务流程实例的数量,又可以增加事件日志的机密性[13]。CARMONA等[14]建议基于轨迹的Parikh向量来检测事件日志中的行为,然而这种采样技术不能用于流程发现,因为Parikh向量并不存储对发现流程模型至关重要的活动序列。为了简化流程发现算法在大规模数据集上的应用,BERTI[15]提出一种针对启发式流程挖掘算法(heuristic miner)[3]的统计抽样技术;LIU等[16]提出一种基于图的事件日志抽样排序模型LogRank,该模型基于Google的PageRank[17],对事件日志中的轨迹进行了重要性排名。对于抽样方法效用的评价,SANI等[18]比较了多种偏置抽样方法在不同数据集上的表现,发现与随机抽样相比,采用偏置抽样可以大大加快流程发现技术的速度。
2 预备知识
定义1日志、轨迹、事件。事件e指流程执行过程中发生的活动,包括活动名称和时间戳等特征属性。所有事件的集合表示为ε,即e∈ε。事件的有序执行构成一个序列σ=e1,…,en,称为轨迹,其中ei表示轨迹中第i个发生的事件。事件日志L={σ1,…,σm}是所有轨迹的集合。
表1所示为一个事件日志的示例。其中,每一条轨迹表示一个流程实例执行的完整过程,每个事件表示流程实例中发生的活动。需要说明的是,事件的特征属性除了活动名称和时间戳,可能还有资源、执行者等其他属性,本文只考虑事件的活动名称和时间戳特征属性。

表1 事件日志示例
定义2直接跟随关系。设σ=e1,e2,…,en∈L,则称ei+1直接跟随于ei,记为ei≻ei+1。为了简化表达,通常用事件的活动名称属性代指事件。
以表1中的事件日志为例,记σ1=A,B,C,称B直接跟随于A,C直接跟随于B,以此类推。
定义3信息增量。设采样日志为L′,L′是完整事件日志L的子集。若一条轨迹σ含有采样日志集合L′中未包含的信息,则认为该轨迹是一条带有新信息的轨迹,用γ(L′,σ)=1表示;反之,γ(L′,σ)=0。
在逐条遍历事件日志中的轨迹时,采用抽象函数Ψ提取轨迹中的信息。
定义4控制流(Control Flow)抽象函数。给定一条轨迹σ,定义控制流抽象函数
ΨCF(σ)(Aσ,≻(σ),estart(σ),eend(σ))。
(1)
式中Aσ为轨迹σ中出现的活动集合;≻(σ)为轨迹σ中事件的直接跟随关系集合;estart(σ)和eend(σ)分别为该轨迹的开始/结束事件。

(2)
以表1中的两条轨迹σ1=A,B,C和σ2=A,B为例,假设采样日志L′中只有σ1一条轨迹,根据式(1)和式(2)可得而ΨCF(σ2)=({A,B},{A≻B},{A},{B}),将σ2加入L′会在中增加新的结束事件,因此认为σ2是一条带有新信息的轨迹,即γ(L′,σ2)=1。
轨迹的特征信息不同于事件的特征信息,除了轨迹ID外,轨迹的其他特征属性一般不会在事件日志中显式地表示,而是通过计算获得,如轨迹中事件的数量、轨迹的持续时间等。仅关注事件日志的控制流信息所能得到的轨迹数量有限,因此本文额外使用轨迹的两个特征(轨迹长度和轨迹持续时间)来减少信息损失。
定义5轨迹/日志长度。轨迹长度指轨迹中发生的事件数量,记为Len(σ)。对于日志L,Len(L)表示日志L中所有轨迹长度的集合。
对于轨迹σ∈L-L′,如果Len(σ)∉Len(L′),则认为轨迹σ是一条带有新信息的轨迹,并记γ(L′,σ)=1。
为了进一步发现流程实例之间的差异,本文用轨迹持续时间来扩充轨迹信息。
定义6轨迹持续时间。轨迹持续时间指一个流程实例从开始执行到结束经过的时间,计算公式为
T(σ)=eend(σ).timestamp-estart(σ).timestamp。
(3)
轨迹的持续时间通常是一个细粒度的数值,从该属性角度看可以认为几乎每一条轨迹都引入了新信息。为了减少时间信息带来的差异,本文用距离函数d和松弛系数λ来判断向L′中加入一条轨迹是否会引入新的信息。σ∈L-L′与L′之间的轨迹持续时间距离
(4)
式中n为L′中轨迹的数量。只有当d(L′,σ)大于设定的松弛系数λ时,才认为该条轨迹引入了新的时间信息。
3 基于轨迹信息增量的日志采样
3.1 总体框架
本文提出的基于轨迹信息增量的日志采样方法的总体流程如图1所示。该方法将完整事件日志作为输入,首先根据统计推断计算出最小连续遍历样本数量Nmin,然后根据控制流和轨迹特征判断每一条轨迹是否带有新的信息,并将其加入采样日志。在连续遍历Nmin条没有新信息的轨迹后,采用二进制指数跳跃算法计算下一次扫描的位置,直到遍历到事件日志的末尾。
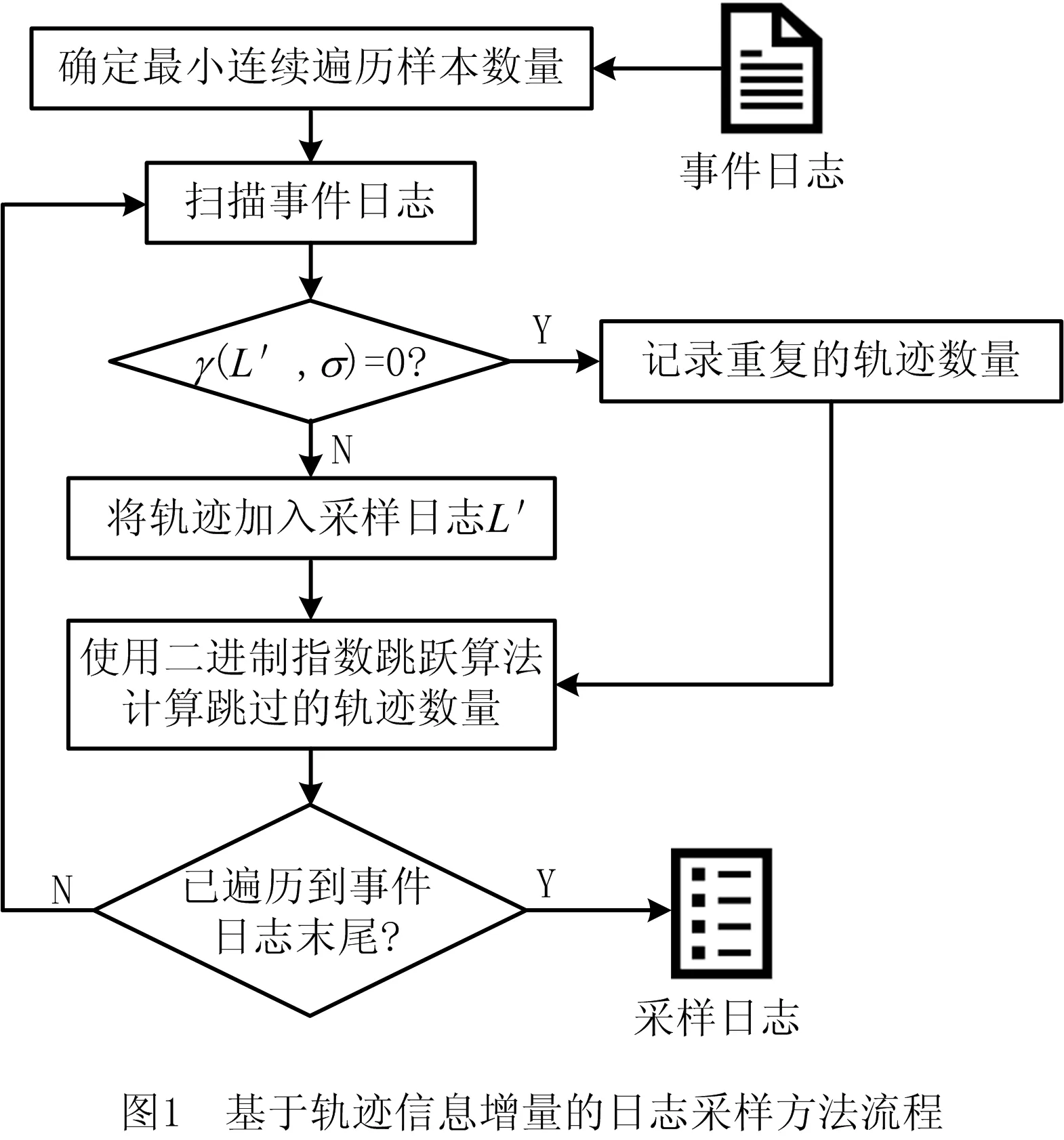
下面详细介绍最小连续遍历样本数量的计算方法以及二进制指数跳跃算法的流程。
3.2 确定最小连续遍历样本数量
本文的研究目的为快速从大规模事件日志中采样出一个高效用的日志子集,其核心思想是避免完整扫描事件日志,即在未知事件日志中轨迹行为分布的情况下进行局部采样。
基于上述动机,本文基于统计原理作出以下假设:假设L中的每一条轨迹均为独立同分布,从L中选取n条轨迹样本,定义p=pi为轨迹σi带有新信息的概率,即对所有轨迹而言,带有新信息的概率pi均相同;对于一条轨迹σi,γ(L′,σi)只有1(带有新信息)或0(不带有新信息)两种取值。在此假设之下,可以认为n条样本轨迹中含有新信息的轨迹数量x符合二项分布,即x~B(n,p),在事件日志数量足够大的情况下,二项分布近似于正态分布。
样本量对于获得准确的、具有统计意义的结果非常重要,本文基于Cochran公式[19]计算这一理想样本量。给定置信水平α、概率约束δ和误差幅度e,最小连续遍历样本数量
(5)
式中:z对应于置信水平1-α(单边假设检验)的标准化正态随机变量;δ为在L-L′中发现带有新信息的轨迹的概率。误差幅度一般取5%。
例如,当α=0.01且δ=0.05时,由式(5)可得Nmin≥126,即当在日志L中连续遍历了126条不带有新信息的轨迹之后,可以认为在剩余日志中发现带有新信息轨迹的概率小于0.05,其置信水平为0.99。
3.3 二进制指数跳跃算法
上述内容从统计理论层面证明,在原始事件日志中扫描了一定数量不带有新信息的轨迹后,可以认为在后续日志中出现带有新信息的轨迹的概率很小。然而,在真实的事件日志中,相似的流程行为(即无信息增量的轨迹)可能会在一段时间内大量出现,将其称为相似轨迹聚集现象。如果扫描了Nmin条相似轨迹之后就停止采样,则可能无法在后续事件日志中发现新的轨迹,从而出现信息损失。
为了避免相似轨迹聚集导致的信息损失,本文提出二进制指数跳跃算法,在连续扫描Nmin条没有信息增量的相似轨迹后,重新计算下一次扫描的间隔,从而跳过一部分不带有新信息的轨迹,以保证在后续事件日志中发现新轨迹,同时提高预处理的速度。
若在原始事件日志中连续遍历了Nmin条不带有新信息的轨迹,则认为此处发生相似轨迹聚集,此时从离散的整数集合[1,2,…,2k]中随机取出一个数作为下一次扫描前需要跳过的轨迹数,其中参数k的计算公式为
k=min(发生轨迹聚集的次数,8)。
(6)
扫描的间隔与发生轨迹聚集的次数有关。当k≤8时,参数k等于发生轨迹聚集的次数,从[1,2k]中随机选取一个整数作为要跳过的轨迹数量;当k>8时,从[1,28]中随机选取一个整数。一旦扫描到一条带有新信息的轨迹时,即将k恢复为默认值1,并重新开始相似轨迹的计数。
二进制指数跳跃算法提供了一个应对相似轨迹聚集现象的方法。在刚开始出现轨迹聚集时,该算法会以一个相对较小的跳跃间隔决定下一条轨迹的索引;而当相似轨迹聚集频繁出现时,扫描间隔将会以指数级增加,以快速检测出下一条带有新信息的轨迹。二进制指数跳跃算法有助于提高在完整事件日志中发现新轨迹的效率,同时避免完整遍历事件日志导致处理时间过长的问题。
3.4 基于轨迹信息增量的日志采样算法
基于上述理论,本文提出基于轨迹信息增量的日志采样算法,该算法首先根据控制流和轨迹特征属性判断原始事件日志L中的轨迹是否带有新的信息,并将其加入采样日志L′,然后根据相似轨迹聚集的情况决定是否需要采用二进制指数跳跃算法跳过轨迹。算法1描述了基于轨迹信息增量的日志采样过程。
算法1基于轨迹信息增量的日志采样算法。
输入:事件日志L、置信水平α、概率约束δ、误差幅度e、松弛系数λ。
输出:采样日志L′。
1: L′←∅
2: count←0 //记录重复轨迹的数量
3: i←0 //轨迹的索引
4: k←1 //记录发生相似轨迹聚集的次数
5: N←(z2*δ*(1-δ))/(e2) //按式(5)计算最小连续遍历样本数量
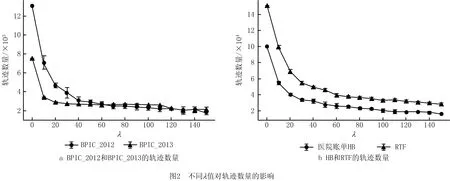
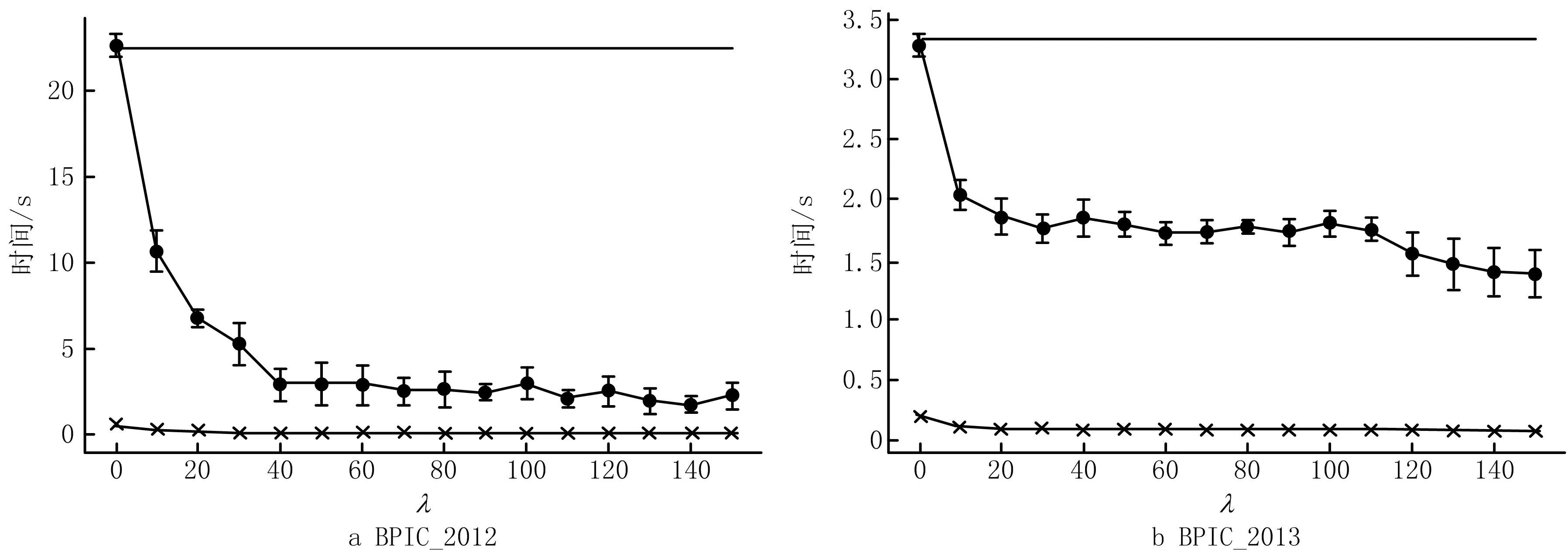
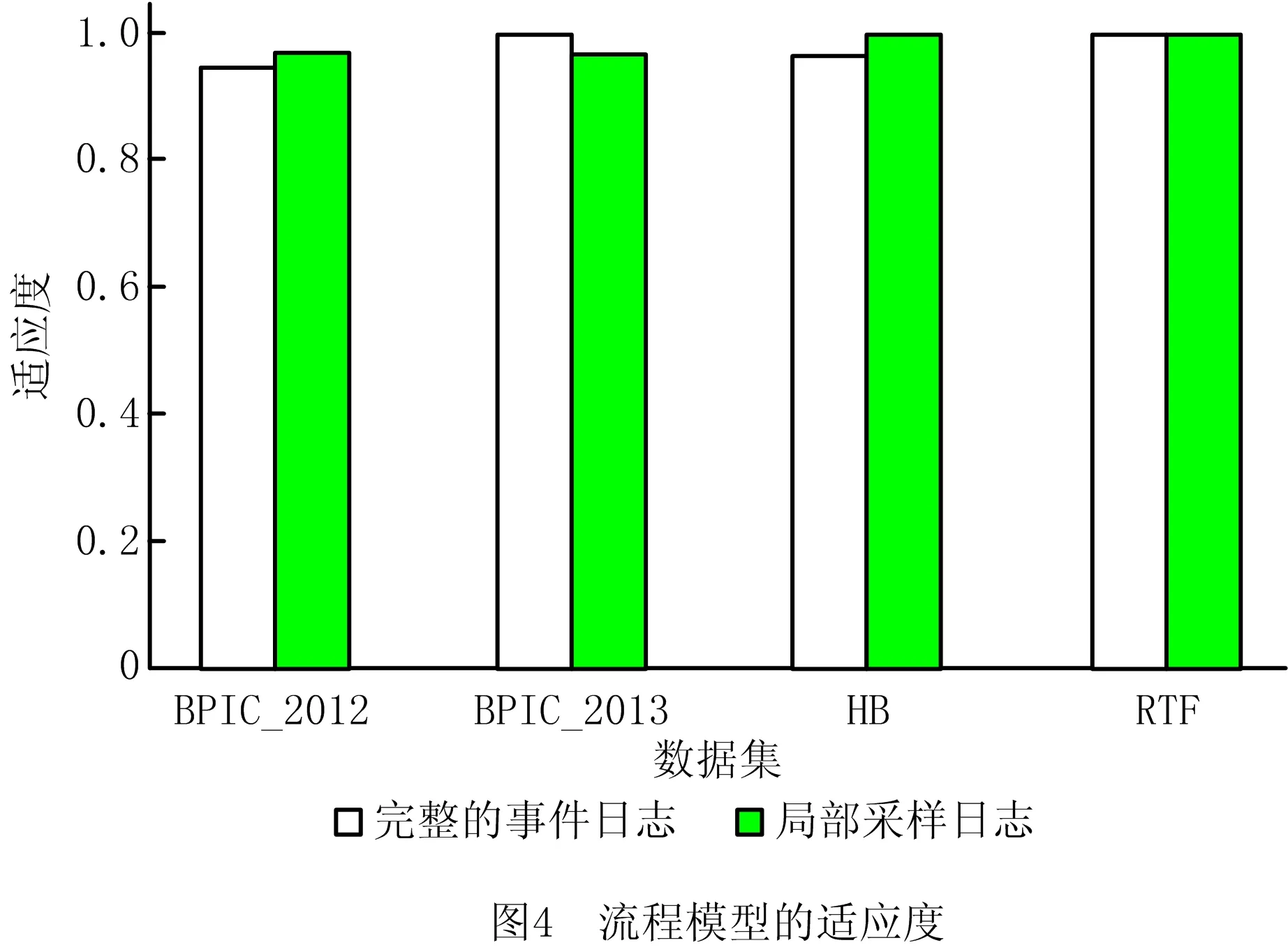
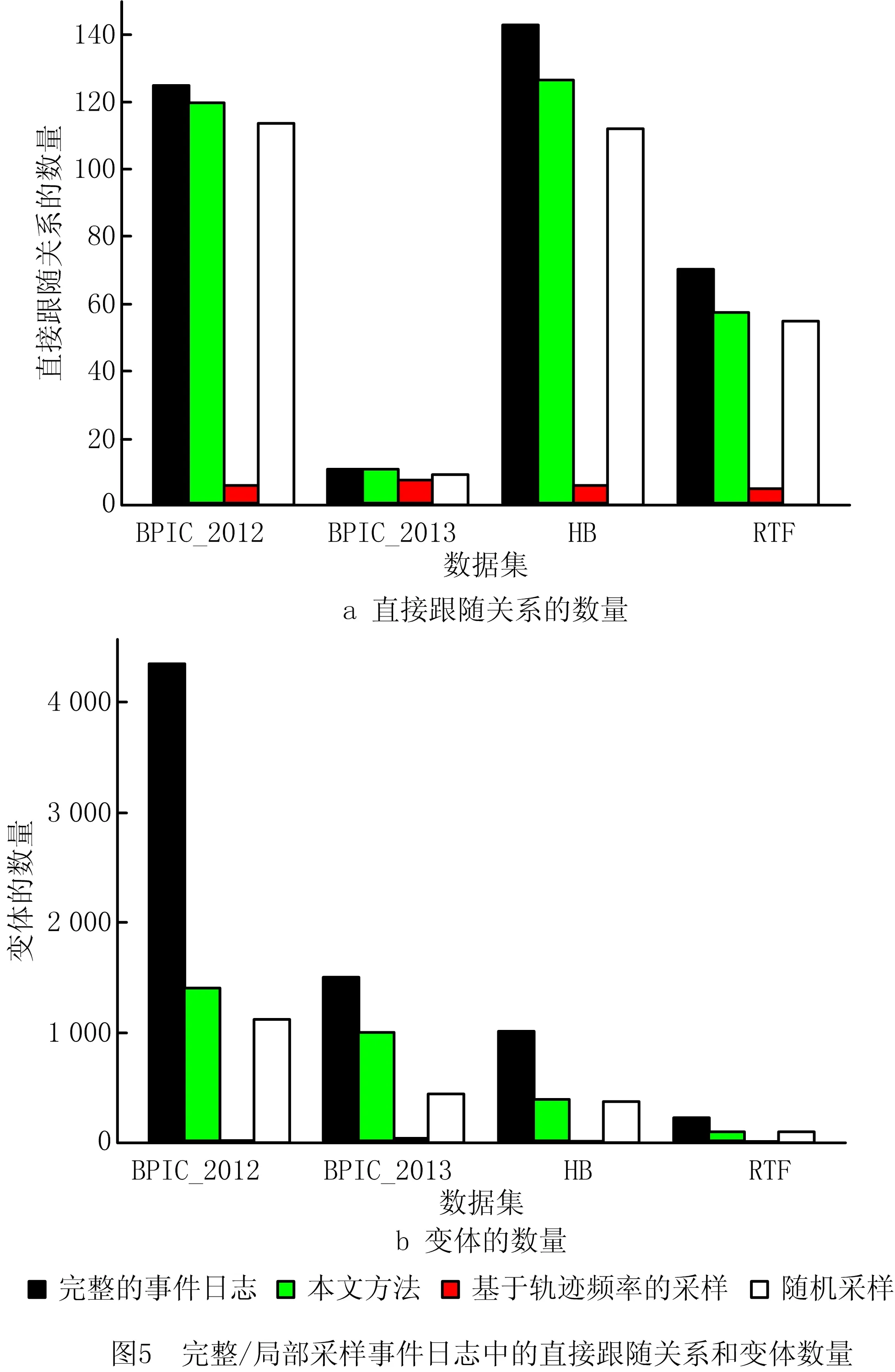
6: WHILE i 7: σ←从L中取出一条轨迹 8: γ(L′,σ)←calculate γ(L′,σ) with bound of λ //根据控制流和特征属性计算轨迹是否带有新信息 9: IF γ(L′,σ)=1 THEN 10: count←0 11: k←1 12: ELSE 13: count←count+1 14: IF count>N THEN 15: k←k+1 16: END IF 17: END IF 18: L′←{σ}∪L′ //将轨迹加入采样日志 19: IF count>N THEN //采用二进制指数跳跃算法确定需要跳过的轨迹数量 20: k←min(k,8) 21: i←i+random(1,2k) 22: ELSE 23: i←i+1 24: END IF 25:END WHILE 26:RETURN L′ 算法1将原始事件日志L、置信水平α、概率约束δ、误差幅度e和松弛系数λ作为输入,在初始化后(第1~4行),根据式(5)计算出最小连续遍历样本数量Nmin(第5行);然后顺序遍历事件日志,根据式(1)~式(4)计算并判断每条轨迹是否带有新的信息(第7~8行);若当前轨迹带有新的信息,则重置计数器count和参数k,并将该轨迹加入采样日志(第9~18行);若连续扫描了Nmin条没有新信息的轨迹,则采用二进制指数跳跃算法计算下一次扫描的轨迹索引,直到遍历到事件日志的末尾(第19~24行)。 毫无疑问,采用二进制指数跳跃算法在提高预处理速度的同时会引入一定信息损失,然而这种情况对日志采样的影响未必是负面的。因为事件日志本身就存在一些低频率的流程行为,这些行为使发现的流程模型变得复杂而难以分析,所以目前许多流程发现算法都采用噪声过滤机制或单独的预处理步骤事先过滤掉事件日志中的低频行为。由于在二进制指数跳跃算法执行过程中跳过的轨迹大概率是事件日志中发生频率较低的轨迹,所带来的信息损失可以看作为噪声处理步骤的一部分,其对流程模型的发现有积极的作用,这部分内容将在第5章通过适应度(fitness)实验详细论证。 本文实验采用Python语言编写(Python的版本为3.6.5),采用PM4PY库对事件日志进行统计分析。实验环境配置如下:操作系统为Windows 10专业版64位;处理器为Intel(R) Core(TM) i7-6500U (2.50 GHz);内存为12.0 GB。 本文采用归纳算法Inductive Miner的一种变体——IMi(inductive miner infrequent)作为流程发现算法。IMi算法根据事件的直接跟随关系将日志转化为直接跟随图,并基于事件发生的频率处理日志中的不频繁行为(噪声),使其可以适用于真实的事件日志。本实验用默认值0.2作为IMi算法的噪声阈值。在对事件日志采样时,设置α=0.01,δ=0.05,松弛系数λ是实验中的一个可控变量,所有实验均取10次实验运行结果的平均值作为最终结果。 本文选择在4个公开的真实事件日志数据集上验证日志采样算法的有效性。所有数据集均来自4TU Centre for Research Data (https://data.4tu.nl/),数据集的详细信息如表2所示。 表2 真实事件日志的详细信息 本文从3个方面评价日志采样算法的性能: (1)轨迹数量、直接跟随关系数量和变体数量 通过比较采样日志的大小,即采样日志中包含的轨迹数量,来衡量采样的有效性。除轨迹数量外,本实验还将研究采样日志中保留的事件直接跟随关系和变体的数量。 (2)效率 效率分为采样时间和挖掘时间两部分。采样时间指对原始事件日志进行预处理的时间,挖掘时间指从采样日志中发现流程模型的时间。将采样时间和挖掘时间拟合得到效率的值,效率(ms)=采样时间(ms)+挖掘时间(ms),然后与从完整事件日志中挖掘出流程模型的时间进行比较。 (3)适应度 用于评估流程模型捕获了多少事件日志中的行为,当适应度取值为1时,表示流程模型可以完美地描述日志中存在的所有行为。实验首先从采样日志中挖掘出流程模型,然后采用基于标记重放的一致性检查方法[20]在流程模型上重放原始的事件日志,从而计算出流程模型的适应度。 实验1探究日志采样的有效性,图2所示为不同λ值对采样日志中轨迹数量的影响,作为参考值,λ=0时采样日志中的轨迹数量与原始事件日志中的相同。可见在4个数据集上,随着松弛系数λ的增加,轨迹数量均呈现下降趋势,并在λ值较大时趋于平稳。值得注意的是,在λ=20时,所有数据集的轨迹数量都下降到了原始数量的40%左右,说明在真实事件日志中,大部分轨迹(60%左右)在持续时间上的差异比较小(小于20),因此轨迹数量会在λ为0~20这一阶段大幅下降。图2证明本文采样方法可以有效减小事件日志的规模。 减小事件日志规模可以有效提高流程发现的效率,图3所示为在4个数据集上进行采样和流程挖掘的时间。随着松弛系数λ值的增加,采样的日志规模越小,流程挖掘的总体效率越高,说明IMi挖掘算法的执行时间和事件日志规模成正比,通过采样减小事件日志的规模是提高效率最有效的手段。本文采样方法使IMi算法的挖掘速度在4个数据集上均有不同程度的提高,表3所示为λ=150时IMi算法在完整日志和采样日志上挖掘的效率差异。除此之外,图3还单独标出了进行日志采样花费的时间,这一时间相对于采用IMi算法进行流程发现的时间可以忽略不计,证明本文的采样算法十分高效。 表3 IMi算法的挖掘效率(λ=150) ms 图4所示为采用IMi算法从完整/局部采样日志中挖掘出的流程模型的适应度差异。因为IMi算法自身带有噪声过滤机制,所以在4个数据集上,从完整事件日志中挖掘出的流程模型的适应度均未达到1,但都在0.95以上,而从采样日志中挖掘出的流程模型在4个数据集上的适应度也都达到和完整日志相近的水平,证明大规模事件日志中的确存在大量重复的轨迹,使用完整日志的一小部分就可以发现较高质量的流程模型,而且采样日志中高频行为的比例与完整日志中相似。特别地,图4显示二进制指数跳跃算法造成的信息损失对流程模型适应度的影响不同。在BPIC_2013数据集上,从采样日志中挖掘出的流程模型比从完整事件日志中挖掘出的流程模型的适应度低,说明二进制指数跳跃算法跳过了一些带有新信息且发生频率较高的轨迹,可能因为本文设置的扫描跳跃间隔对于小规模数据集范围过大。而流程模型在数据集BPIC_2012和数据集HB上的适应度略高于从完整事件日志中挖掘出的流程模型,原因是采用基于信息增量的采样方法捕获且放大了原始事件日志中的低频行为,这些行为包含额外的控制流信息,从而使流程模型能更完美地匹配事件日志。在RTF数据集上,两个流程模型的适应度几乎相同,证明二进制指数跳跃算法带来的信息损失与IMi的噪声过滤机制类似,即跳过的轨迹为原始事件日志中的低频率轨迹。 实验2对不同的采样策略性能进行比较。实验采用基于轨迹频率的采样方法,并将随机采样方法作为对照,其中基于轨迹频率的采样方法选取事件日志中发生频率最高的轨迹加入采样日志,随机采样方法则随机地从事件日志中抽取轨迹。为了保证实验的公平性,在所有数据集上都将采样率控制在30%左右(采样率=采样日志的大小/完整日志的大小)。 直接跟随关系是体现控制流信息最关键的因素,采样日志能在多大程度上保留直接跟随关系决定了流程模型的最终结构。图5a所示为基于不同采样策略得到的采样日志中保留的直接跟随关系的数量。该结果表明,本文采样方法能够保留原始日志中88%以上的直接跟随关系,特别在BPIC_2013数据集上,采样日志保留了所有的直接跟随关系。图5b所示为不同采样日志中保留的变体数量之间的差异。变体是一组共享相同控制流信息的轨迹,即轨迹中活动出现的顺序相同,不同变体之间的直接跟随关系可能相同,因此并不是每一个新的变体都会在流程模型中提供新的信息。以BPIC_2012数据集为例,采样日志仅保留了1 422种流程变体(总共有4 366种流程变体),而这些变体涵盖了96%的直接跟随关系(120/125),即本文采样算法虽然过滤掉了大部分直接跟随关系重复的变体,大大减少了事件日志的规模,但是仍然能从日志中挖掘出高质量的流程模型。除此之外,图5中基于轨迹频率的采样方法得到的直接跟随关系和变体数量都很少,这是由于相同控制流的轨迹在事件日志中大量重复出现导致的;而随机采样方法虽然可以发现更多的控制流信息,但是仍然少于本文的采样方法。 最后从采样时间上比较不同策略的性能,如图6所示。在3种采样方法中,速度最快的是随机采样,原因是该方法无需进行额外计算。本文方法仅次于随机采样,证明采用二进制指数跳跃算法避免对完整日志进行扫描可以有效提高采样效率。 本文提出一种基于轨迹信息增量的日志采样方法,首先从事件日志中抽象出控制流信息和特征属性信息,用于比较轨迹携带的信息量;然后采用二进制指数跳跃算法避免遍历重复或相似轨迹,达到提高预处理效率的目的。在4个真实事件日志上的实验表明,本文采样方法可以快速有效地将大规模的事件日志采样到一个可管理的大小,能够保证从采样日志中挖掘出的流程模型的质量。未来将比较各种采样策略的有效性,并在发生流程概念漂移的情况下对新版本的流程日志进行区分和采样。4 实验设计
4.1 实验环境与参数设置
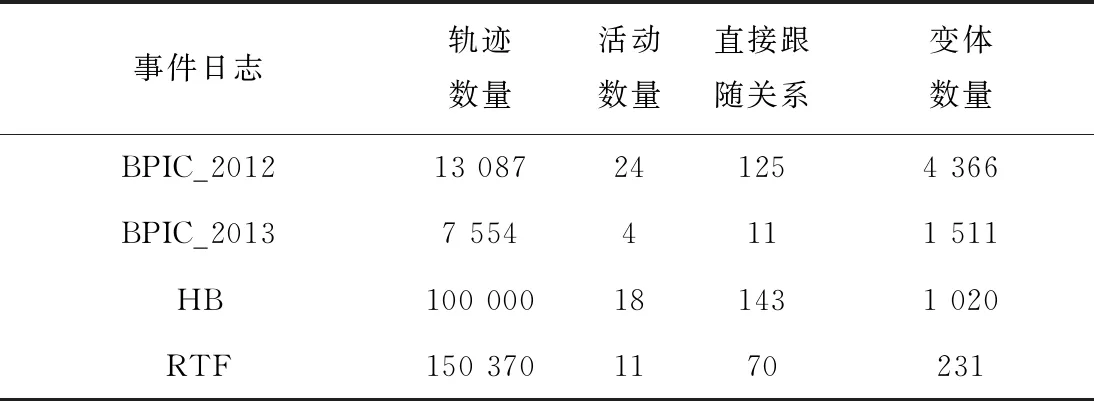
4.2 实验数据
4.3 评价指标
5 实验结果



6 结束语
