不锈钢圆管T形、Y形相贯节点支管受拉承载力研究

郑宝锋，吴步宸，张 奎，王嘉昌，舒赣平，蒋庆林

(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096；2.东南大学 土木工程学院，江苏 南京 210096；3.中国建筑西北设计研究院有限公司，陕西 西安 710018；4.江苏东阁不锈钢制品有限公司，江苏 盐城 224000)

随着国家经济的高速发展，人们对建筑外观要求越来越高.不锈钢结构不仅具有优异的耐腐蚀性能，还具有良好的力学性能和加工性能，在民用和工业建筑中具有广泛的应用前景.管结构由于造型美观，节点构造简单、受力性能良好，在我国应用越来越广泛.在不锈钢结构领域，我国学者进行了大量的研究，但是，对不锈钢相贯节点性能研究尚未广泛开展.基于以上背景，本文对不锈钢圆管T形、Y形相贯节点进行支管轴向拉力作用下的承载力研究.

在不锈钢材料性能方面，王元清等[1]、王萌等[2]和常笑等[3]对不锈钢力学性能进行研究，舒赣平等[4-5]和袁焕鑫等[6]对不锈钢受压构件进行研究.在不锈钢相贯节点研究方面，Rasmussen等[7-8]对不锈钢X形、K形相贯节点变形及承载力进行了研究，结果表明：采用残余应变为0.2%和0.5%的应力替换国际管结构协会设计手册(CIDECT，1st)[9]设计公式中的屈服强度可用于节点承载力的计算.Feng和Young[10-12]对冷弯不锈钢方管相贯T形、X形节点进行试验研究与数值分析，结果表明：残余应变为0.2%的应力替换CIDECT[9]设计公式中的屈服强度，能较好地预测不锈钢管T形、X形节点在正常使用极限状态和承载力极限状态下的承载力.Zheng等[13]对不锈钢圆管K形相贯节点进行了研究，通过试验研究及参数化分析，对CIDECT[14]公式中考虑几何因素的因子Qu和考虑弦杆预加载荷因素的因子Qf进行修正.Wang等[15]对不锈钢圆管T形、Y形相贯节点支管受压性能进行了研究，结果表明，使用CIDECT规范计算的节点承载力偏保守.根据参数化分析结果对CIDECT[14]公式中的Qu和Qf对弦杆塑性破坏的作用进行修正.Zheng等[16]对不锈钢方管K形节点进行了研究，提出了一种兼顾弦杆连接面和弦侧壁变形的屈服线破坏机理，改进了K形节点承载力计算方法.此外，Feng等[17]、Lan等[18]和张哲文等[19]对不锈钢相贯节点的高温和疲劳等性能进行了研究.

从研究现状可知，国内外暂无对支管受拉不锈钢圆管相贯节点的试验研究，为此，本文通过节点试验，获得节点的破坏模式和承载力，并建立有限元模型，分析支管受力状态对节点承载力的影响.

1 试验研究

1.1 节点试件设计

设计和制作了9个不锈钢圆管相贯节点，其中T形节点6个，Y形节点3个，材料均为奥氏体型304冷成型不锈钢钢管.T形、Y形节点弦杆与支管之间的夹角分比为90°和45°.焊缝采用氩弧焊，焊脚尺寸根据CIDECT[14]的规定取值，详见表1.试样的表面在焊接后进行了喷砂处理.

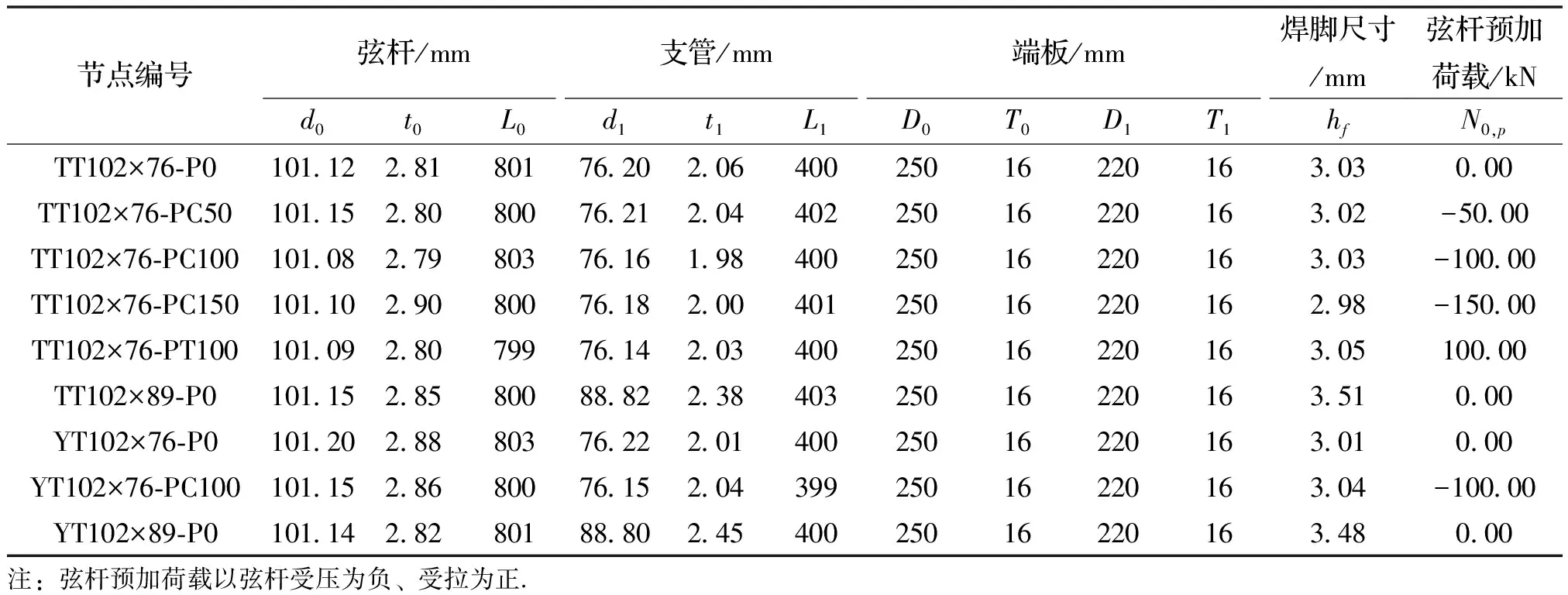
表1 不锈钢圆管T形、Y形节点的测量尺寸和弦杆预加载荷

在试件设计中，以支管与弦管的管径比β和弦杆预加荷载N0,p为主要参数.支管的公称直径分别为76 mm和89 mm，厚度分别为2 mm和2.5 mm，弦杆的公称直径为102 mm，厚度为3 mm，管径比β分别为0.75和0.87.对于T形节点试件，在-150～100 kN范围内设计5种不同弦杆预加荷载；对于Y形节点试件，在-100～0 kN范围内设计2种不同弦杆预加荷载.预加荷载在弦管产生的轴向应力比为0.3～0.5.弦杆和支管的轴线长度(L0和L1)分别为800 mm和400 mm.从节点区到弦管端部加载处的长度约为截面直径的4倍，加载端处应力对节点区应力的干扰可以忽略.弦杆两端和支管末端焊接Q345钢材的圆形端板，试验中通过6颗高强螺栓连接耳板.试样如图1所示，测量尺寸如表1所示.

表1中，d0、t0、L0分别为弦杆的直径、壁厚和长度；d1、t1、L1分别为支管的直径、壁厚和长度；D0、T0分别为焊接到弦杆的端板的直径和厚度；D1、T1分别为焊接到支管的端板的直径和厚度；hf为焊脚尺寸；N0,p为设计的弦杆预加载荷.

节点编号的规则以TT102×76-PC50为例，首字母T表示T形节点(Y表示Y形节点)；第二个T表示支管的受力形式为受拉；102和76分别表示弦杆和支管外径；PC表示弦杆预加荷载为压力(PT表示弦杆预加荷载为拉力)；50表示以kN为单位的预加载荷值.

1.2 材料性能试验

使用自动电火花丝切割机分别从三种截面构件中各取出3个试件，总计9个材性试件.依据《金属材料拉伸试验 第1部分：室温试验方法》(GB/T228.1—2010)[20]进行标准拉伸试件设计.试验在10t CMCT5105电子万能试验机上进行.试验中试件前后表面粘贴两个应变片(BX120-3AA)测量应变.试验速率为0.5 mm/min，试验装置及拉伸破坏如图2所示.

选用Gardner模型[21]处理试验数据，如公式(1)所示，其中：E0表示杨氏模量；σ0.2表示0.2%屈服应力；σ1.0表示1.0%屈服应力；σu表示极限拉应力；n表示Ramberg-Osgood模型σ0～σ0.2之间的应变硬化指数；n0.2,1.0表示σ0.2～σ1.0之间的应变硬化指数.数据处理结果如表2所示.

表2 材料性能试验结果

(1)

1.3 节点试验

节点加载装置示意图和加载实物图分别如图3(a)和(b)和图4(a)和(b)所示.该反力架可用于弦杆施加预加压力或拉力荷载条件下，T形、Y形支管的受拉或受压试验.试验中弦杆左、右侧均为滑动铰支座，可以在支座长圆孔方向(弦杆轴向)滑动；支管端部为滑动铰支座.Y形节点加载方式与T形节点相似，仅改变支管加载千斤顶的位置.

1.3.1 试验测量内容及加载制度

采用位移计测量节点位移和变形.T形节点位移计布置如图5(a)和(b)所示，图中DG-X表示位移计编号.在支管端板两边各布置一个位移计，用以获取加载端的位移.在弦杆跨中布置竖向位移计，同时在距离跨中100 mm，左右各布置一个位移计，弦杆跨中竖向位移计可以用来记录弦杆下表面的竖向变形.在弦杆前后两侧各设置三个位移计，用于记录弦杆管壁的侧向变形.冠点左右两侧各布置一个位移计，用于测量弦杆上表面的变形.Y形节点位移计布置如图6(a)和(b)所示，由于空间限制，仅在冠点一侧布置位移计，其余布置与T形节点位移计布置一致.

试验中首先施加弦杆预加荷载，并在后续加载中手动保持不变.正式加载前，施加初始载荷(小于预测最终载荷的5%)以消除间隙并检查数据采集系统.随后进行正式加载，缓慢施加支管轴力，直到节点破坏.使用数据采集设备(TDS303)连续记录位移计的读数和施加的荷载(压力传感器).

1.3.2 试验结果

试验现象如图7、图8所示.其中，T形和Y形节点的破坏模式相似，均为节点域弦杆的塑性变形.加载初期，支管带动弦杆向上运动，弦杆的变形类似于跨中施加向上集中拉力的简支梁，表现出明显的弯曲，节点域变形微小.当加载到一定阶段，跨中弦杆侧壁开始向内收缩，弦杆截面由原来的圆形变为椭圆形，但是变形值很小；继续加载时，节点承载力不断提高，没有下降的趋势，当弦杆弯曲到一定程度，弦杆下表面在压应力作用下发生局部凹陷，节点承载力急剧下降.其中，YT102×76-PC100节点加载过程中因操作失误，未能记录完整的荷载位移曲线.

图9、10分别表示T形、Y形节点支管轴向荷载与弦杆跨中侧向和竖向变形之间的关系.其中，弦杆跨中侧向变形采用弦杆跨中两侧位移计(DG-2与DG-5)记录结果的平均值，以向外鼓曲为正、向内凹陷为负，用来表示弦杆侧向变形；弦杆竖向变形为T形节点冠点两侧位移计(DG-10与DG-11)的平均值或Y形节点冠点处位移计(DG-10)与弦杆底部位移计(DG-8)的差值，以变大为正、变小为负.从图9中可以看出，T形节点在支管承受轴向拉力作用下，弦杆中预加轴向压力荷载越大，荷载位移曲线越低；弦杆中预加轴向拉力荷载时，荷载位移曲线升高.根据CIDECT[14]中圆管相贯节点的极限变形条件，节点的承载力取为3%d0局部变形对应的荷载.当弦杆侧向与竖向变形均达到3%d0，则节点的承载力取二者对应荷载的较小值，若其中一个方向变形未达到变形限值，则取另一个方向上变形限值对应的荷载值作为该节点的承载力.图中竖向虚线表示CIDECT手册中规定的节点变形限值，即为3%d0，从图9(a)中可以看出，弦管竖向变形为3%d0时对应的荷载比侧向变形对应的荷载小，即节点区竖向变形对节点承载力起控制作用.表3中给出了节点的承载力.

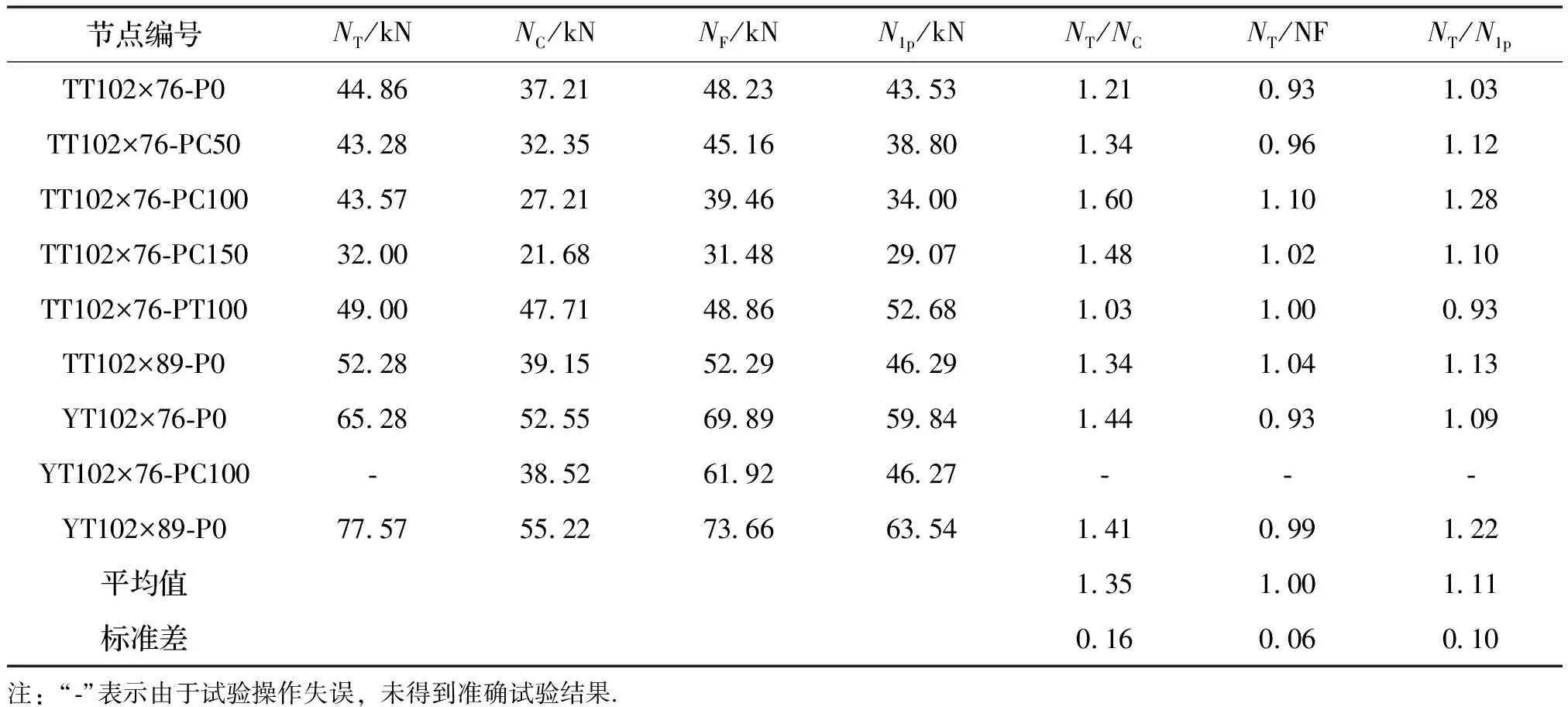
表3 节点试验结果及其与有限元、现行方法预测值的比较

从图10中的荷载-位移曲线可以看出，弦杆侧向变形均未达到极限变形条件，节点的极限承载力由弦杆节点区竖向变形控制.

表中，NT表示试验获得的节点承载力；NC表示按CIDECT计算得到的承载力；NF表示有限元极限承载力；N1p表示按文献[15]提出公式计算得到的承载力.

2 数值模拟与参数化分析

2.1 有限元建模

采用ANSYS软件建立节点分析模型.模型的几何尺寸采用试验试件实测尺寸，材料性能采用表1中的试验结果平均值.有限元模型中采用SHELL181壳单元.考虑到弦杆与支管交叉区域应力分布复杂，故加密该区域的网格，同时有限元模型中的边界条件与试验中相同，如图11所示.

为了能精确地模拟杆端铰接，采用CERIG命令，在圆管端部截面形心处设置一个节点，定义该节点单元类型为MASS21并与端部截面节点建立耦合，最后在该节点上定义边界条件.

为了考虑连接焊缝的影响，采用Vegte[22]提出的方法，沿着相交点添加了一圈壳单元来模拟焊缝，添加的壳单元厚度为弦杆厚度的一半.焊缝模型如图12所示，其中：a=hf+0.5t0；b=hf；壳体厚度为0.5t0；hf表示焊脚尺寸.焊接部分的材料性能近似地采用了弦杆的材料性能.

有限元分析包括两个加载步：在第一步加载中，将预加载施加于弦杆，并在第二步加载中该预加荷载保持不变.第二步加载施加支管载荷，直至节点破坏.

2.2 有限元模型的对比验证

对9个节点试件进行分析，结果如表3所示.从中可以看出，有限元模型的计算结果与试验结果有很好的一致性.NT/NF的平均比值约为1.00，标准差为0.06.图13为有限元分析得到的T形、Y形节点的典型破坏模式，与试验结果相符较好.同时，有限元分析得到的曲线与试验结果吻合较好(见图14).综上，有限元模型可以准确地预测不锈钢管T形、Y形节点的承载能力.

2.3 参数化分析

为了研究支管受力状态对不锈钢圆管T形、Y形节点承载力的影响，采用有限元方法对表4中三组、共24个不同的不锈钢圆管T形、Y形节点分别在支管轴向拉力和压力作用下的节点承载力进行了计算.试件设计考虑了管径比和径厚比的影响.三组管径比β分别为0.50、0.75和0.90，每组弦杆径厚比2γ分别取25.00、33.33、44.44和62.50.

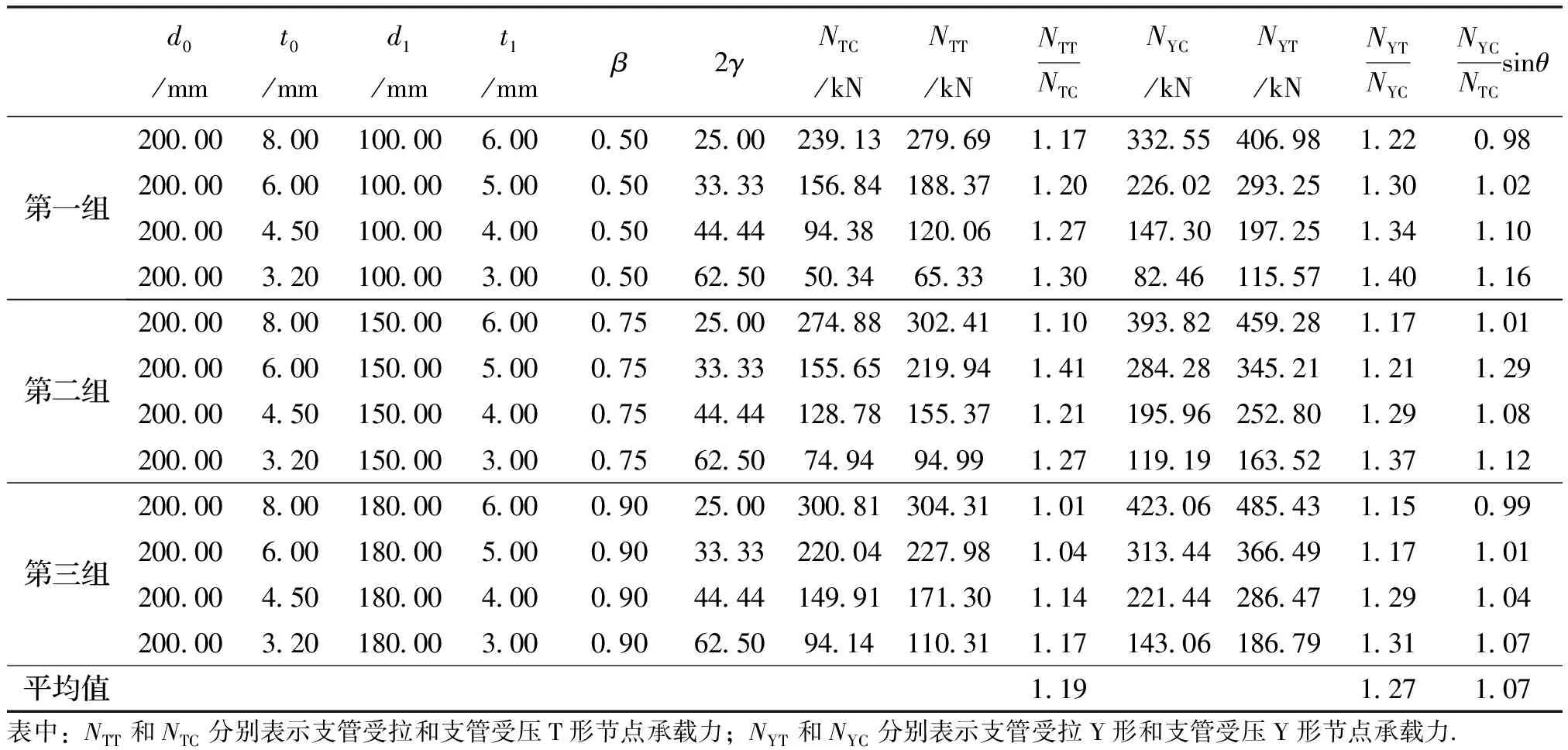
表4 支管受拉、受压不锈钢节点有限元分析基本参数及结果

从表中可以看出：(1)相同边界条件和截面尺寸下，支管受拉的不锈钢相贯节点承载力均高于支管受压的不锈钢相贯节点承载力，其最高值为1.41，二者比值的平均值为1.19，并且随着弦杆径厚比2γ的增大，受拉承载力与受压承载力比值不断提高；(2)由表4中最后一列数据可知，支管受压Y形节点垂直于弦杆的支管承载力分量与相应的支管受压T形节点承载力的比值的平均值为1.07.因此，可以将Y形节点承载力计算简化为相应的T形节点承载力与sinθ之比；(3)节点承载力随β的增加而增加，随2γ的增加而降低.相较之下，参数β的影响大于2γ.

3 节点承载力计算公式

根据参数化分析结果可知，不锈钢圆管T形、Y形相贯节点支管受拉承载力始终大于支管受压承载力.同时，现行设计规范中均采用支管受压状态作为T形、Y形相贯节点的设计控制条件.因此，本文拟采用文献[15]提出的不锈钢圆管T形、Y形相贯节点支管受压承载力公式，对试验节点承载力进行计算.该公式基于CIDECT规范公式，并对其中Qu和Qf进行修正，如式(2)所示.

(2)

式中：N1p为节点承载力的标准值；N0表示弦杆轴力；Npl,0表示弦杆全截面屈服时能够承受的最大轴向荷载；M0表示弦杆上作用弯矩，该弯矩包含支管轴向力引起的弦管弯矩；Mpl,0表示弦杆全截面屈服时承受的弯矩.

将采用公式计算的节点承载力与试验结果及CIDECT计算结果进行比较，如表3所示.由表可得，采用公式(2)计算的节点承载力小于试验结果，大于CIDECT规范计算结果.具体来说，试验结果与公式(2)计算结果的比值平均值为1.11，标准差为0.10；试验结果与CIDECT计算结果的比值平均值为1.35，标准差为0.16.由此表明，采用式(2)计算所得节点承载力偏安全，且精度优于CIDECT计算结果，故可将式(2)应用于支管受轴向力的不锈钢圆管T形、Y形相贯节点设计中.

4 结论

(1)支管轴向拉力荷载作用下的T形、Y形节点的破坏主要为节点域弦杆的塑性变形，节点区域的弦杆最终被拉伸成椭圆形.节点承载力由节点区弦杆局部竖向变形控制，随着弦杆中预加轴向荷载的增大，节点承载力下降；

(2)根据试验结果建立的有限元模型能够准确反映不锈钢圆管相贯节点的真实受力情况，在此模型基础上进行参数化分析，得到不锈钢圆管T形和Y形支管受拉相贯节点承载力始终大于同条件下支管受压相贯节点承载力，比值的平均值分别为1.19和1.27；

(3)文献[15]提出的计算公式可用于支管受拉相贯节点承载力计算，试验值与计算值比值平均为1.11，优于CIDECT公式的预测精度.