基于遗传算法的城市轨道交通大小交路模式列车开行方案研究

安志龙 马丽 崔虎 安志学

（1.陕西铁路工程职业技术学院，陕西 渭南 714000；2.中国铁路呼和浩特局集团有限公司，内蒙古 呼和浩特 010050）

0 引言

随着城市化发展，城市轨道交通线路不同区段的断面客流会出现差异性变化。为了满足不同区段的客流需求，实施按流开行的计划，即在早晚高峰实行大小交路的运营模式，制定大小交路开行方案，有利于提高城市轨道交通的服务水平、降低运营服务成本，同时对推动城市轨道交通碳达峰、碳中和具有重要意义。在理论研究方面，段凌林等［1］以乘客等待时间成本和企业运营成本最小为目标，考虑开行快慢车，并进行大小交路模型的建立与算例的求解；刘兰芬等［2］从列车满载率及乘客舒适度的角度出发，建立以发车间隔时间为最优的模型；牛惠民等［3］以动车组数量和运营企业利益为约束条件，以乘客等待时间最小化为目标函数，结合拥挤环境，构建城市轨道交通开行方案模型；邓连波等［4］利用企业与乘客之间的博弈关系，以列车开行方案的费用和效益为约束条件进行分析，建立了基于弹性需求的城市轨道交通列车开行方案的多目标双层规划模型，设计出模拟退火算法，并对其进行求解；马彩雯等［5］以乘客等待时间与列车行走距离最小化为目标，以发车频率与列车编组为决策量，对西安地铁3号线列车开行方案进行求解。

1 问题的描述

本研究选取单线线路作为研究对象。该线路共有m座车站，定义S1→Sm为上行方向、Sm→S1为下行方向，大交路列车全线大区段运行，小交路列车小区段运行，小交路列车开行列数是大交路的整数倍，车站Sa和车站Sb具备折返功能。

运营期间在车站Si上车，到达车站Sj，下车的上行客流量为、下行客流为，大交路开行列车对数为f1、小交路为f2，且f2=nf1，则在小交路区段内，大小交路列车分担乘客的比率分别为θ=1（1 +n）和1-θ。

基本假设有以下5 个：①在早晚高峰时间段内，列车行车方式均衡（不考虑压道车与调试车）；②大小交路列车折返相互独立，且折返能力满足小交路列车开行频率需求；③列车在车站停车，无越站和跨站情况；④列车在车站停留时间取决于乘客数量与乘客上下车所用的时间；⑤所有计划列车在对应区间的运行时间相同。

2 模型建立

对城市轨道交通服务企业而言，在制定列车开行方案时，主要考虑的是运营服务质量与企业运营成本。因此，为适应客流的随机波动性，以乘客出行在途等待时间成本与开行列车运行成本最小为目标，建立大小交路运营模式下的列车开行方案的模型，并设计出模型优化求解算法。

2.1 乘客出行成本

根据大小交路方案，等待时间成本有大交路时间成本及小交路时间成本。按照上车人数，将线路上行区段客流分为三部分，分别为Q1、Q2、Q3。Q1为［S1，Sa］区段上车的人数且［S2，Sn］区段下车的人数；Q2为［Sa，Sb］区段上车的人数且［Sa，Sb］区段下车的人数；Q3为［Sb，Sn］区段上车的人数且［Sb+1，Sn］区段下车的人数；Q4为[Sa,Sb]区段上车的人数且［Sb+1，Sn］区段下车的人数。

通过分析可知，在全线所有乘客中，只有Q2乘客选择乘坐小交路列车，且各区段乘客数见式（1）至式（4）。

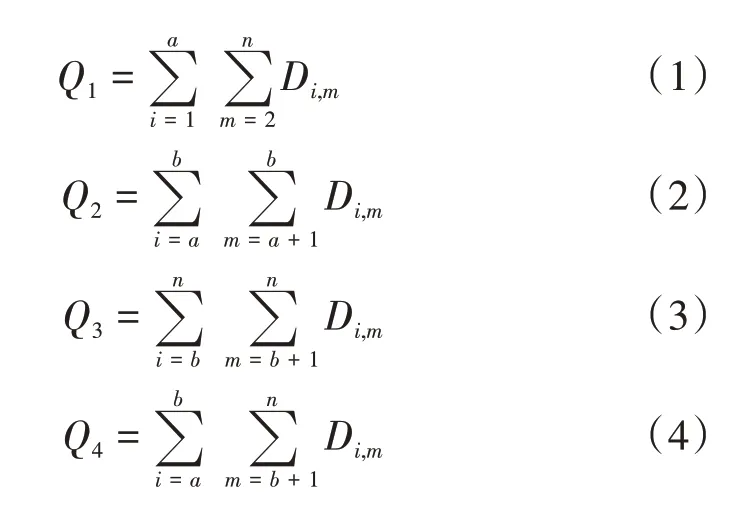
在［S1，Sa］与［Sb，Sn］区段，只有大交路运行车，其大交路行车间隔为tgd=60/f1；小交路行车间隔为tgx=60/f2。设T总为乘客在车站的总等待时间，则乘客车站总等待时间为乘客在大交路区段车站等待时间T大与小交路区段车站等待时间T小之和，见式（5）。

由于在区段［S1，Sa］［Sa，Sb］［Sb，Sn］内的乘客可选择乘坐大交路列车，因此乘坐大交路列车乘客在站等待时间为3 个区段乘客等待时间之和，见式（6）。

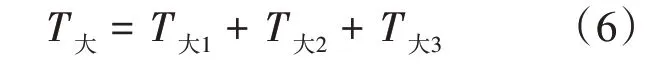
其中，T大1、T大2、T大3、T小的计算公式见式（7）至式（13）。

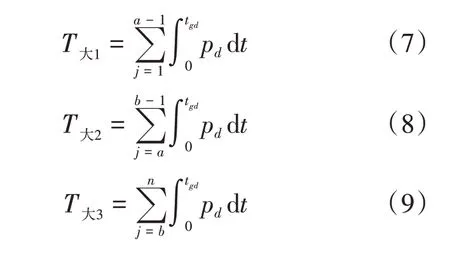
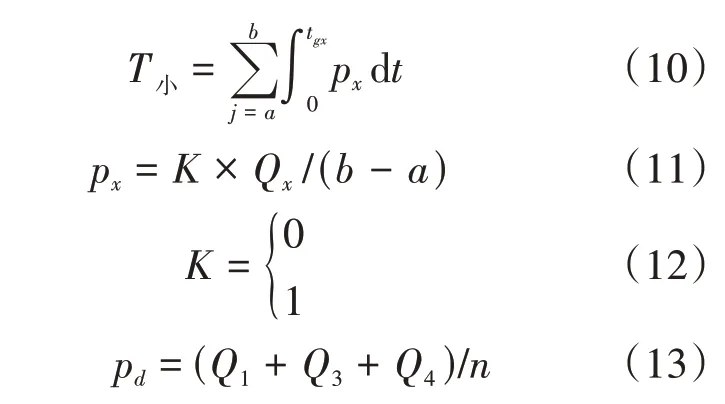
同理可求出下行区段乘客出行在途等待的总时间。

2.2 运营成本

企业的运营成本分为运营固定成本与变动成本。固定成本是指列车采购成本，其在线路建设初期已确定，故在日常运营中只考虑列车总走行千米，则总运营成本的计算公式见式（14）至（16）［8］。

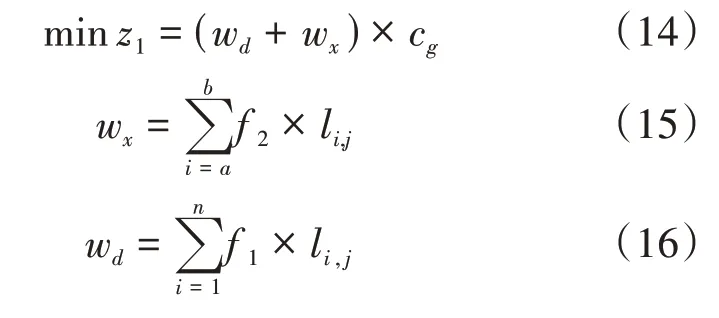
式中：cg为每列开行列车的固定成本，元；lij为车站i到j的里程，km。

2.3 约束条件

2.3.1 列车追踪时间间隔。列车实施按流开车计划，在保证客流的前提下，列车区间追踪时间间隔不能大于线路设计允许的通过能力［9］，即I追踪≤I设计。

2.3.2 列车载客满载率。考虑到列车定员的限制，设载客率为λ，λ取值范围为0.5～1.2。因此，列车实际载客量Ps∈λA，A为列车定员数。

3 模型优化与求解

3.1 模型优化

结合乘客出行成本和运营变动成本，建立双目标规划模型，见式（17）。

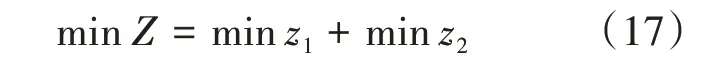
将模型统一量纲后，建立综合模型，并根据最短理想点法来定义评价函数，见式（18）、式（19）。

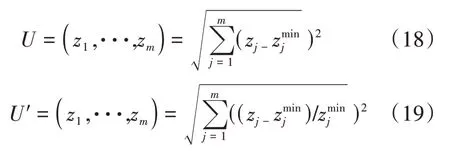
将多目标求解问题转化为单一量纲目标优化问题，见式（20）。

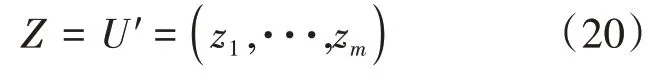
3.2 模型算法的设计

采用自然数编码的遗传算法对模型进行求解，以种群适应度值的大小来判别个体的优劣，运用选择、交叉及变异运算对种群进化改良，产生最优个体，得到最优解。

3.2.1 算法思想。

①编码。大交路停车站数为n，小交路停站数为m（m＜n），f1+f2≤32，且f2≥6。使用自然数编码的方法进行编码，编码时以1～n自然数作为随机数。具体编码方式见图1。

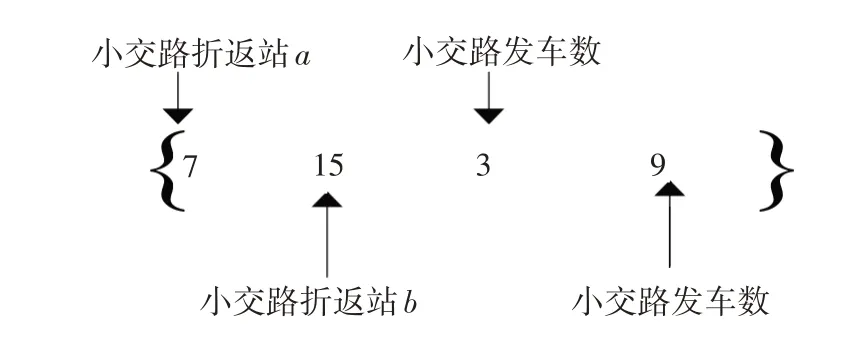
图1 编码方式示意图

其中，小交路折返站a为第7个车站，即a=7；大交路折返站b为第15 个车站，即b=15；小交路发车数为3，即f1=3；大交路发车数为9，即f2=9。

②适应度函数为f(x)=Z(x)。

③选择。采用最优保存稳态复制法，在新一代种群中，留下最优个体不参与交叉与变异运算，直接进入下一代，具体过程如下。

个体在下一代群体中的生存数目为Ni，见式（21）。

④交叉。随机设置2 个交叉点，对2 个交叉点之间的基因进行交换。具体交叉过程见图2。

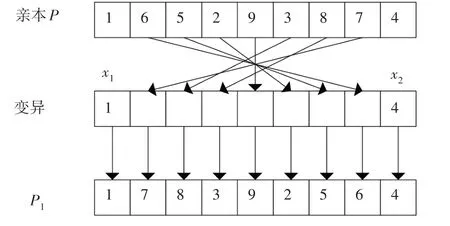
图2 交叉过程示意图

⑤变异。对于给定的亲本P，以异概率为pm从相应取值范围内取随机数k1作为变异点，取随机数k作为k1的值，使其值变为原染色体基因串中k1所对应的值。变异操作过程如图3所示。

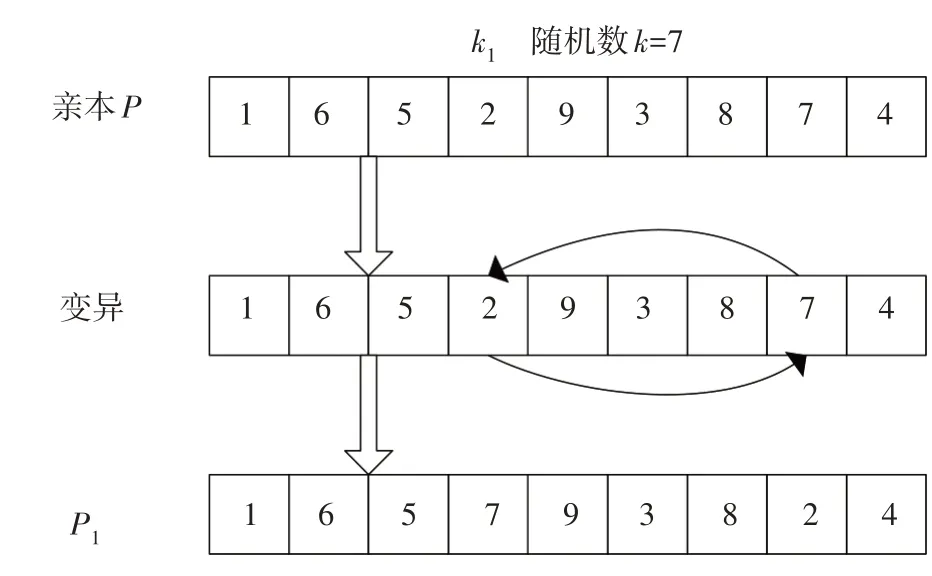
图3 变异过程示意图

3.2.2 算法步骤。算法步骤具体如图4所示。

图4 算法步骤流程图

4 算例分析

4.1 算例数据

以乌鲁木齐地铁1 号线规划及预测数据为例，对本研究设计的模型进行验证。1 号线共有21 座车站，均为地下车站，全线设有百园路车辆段与燕儿窝停车场。车辆采用A型车、6节编组，列车定员为1 860 人/列，平均标准折返时间为118 s，早高峰时段载客率为1.2，单列车运营成本为48 元/km，乘客单位时间价值为0.025 元/s，单位乘客平均上下车时间为0.7 s，最小追踪间隔时间为2 min，最大行车间隔时间为10 min，早高峰为9：00—10：00，客流量占比全日客流的16.8%（见图5），晚高峰时间为19：00—20：00，客流量占比全日客流的14.3%（见图6）。根据本研究所建立的最优车组开行方案模型，利用Maltab 软件进行求解，并计算选择不同折返站的大小交路列车开行数。最后对结果进行分析，确定最优列车开行方案。

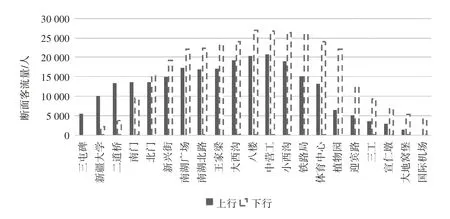
图5 早高峰断面流量

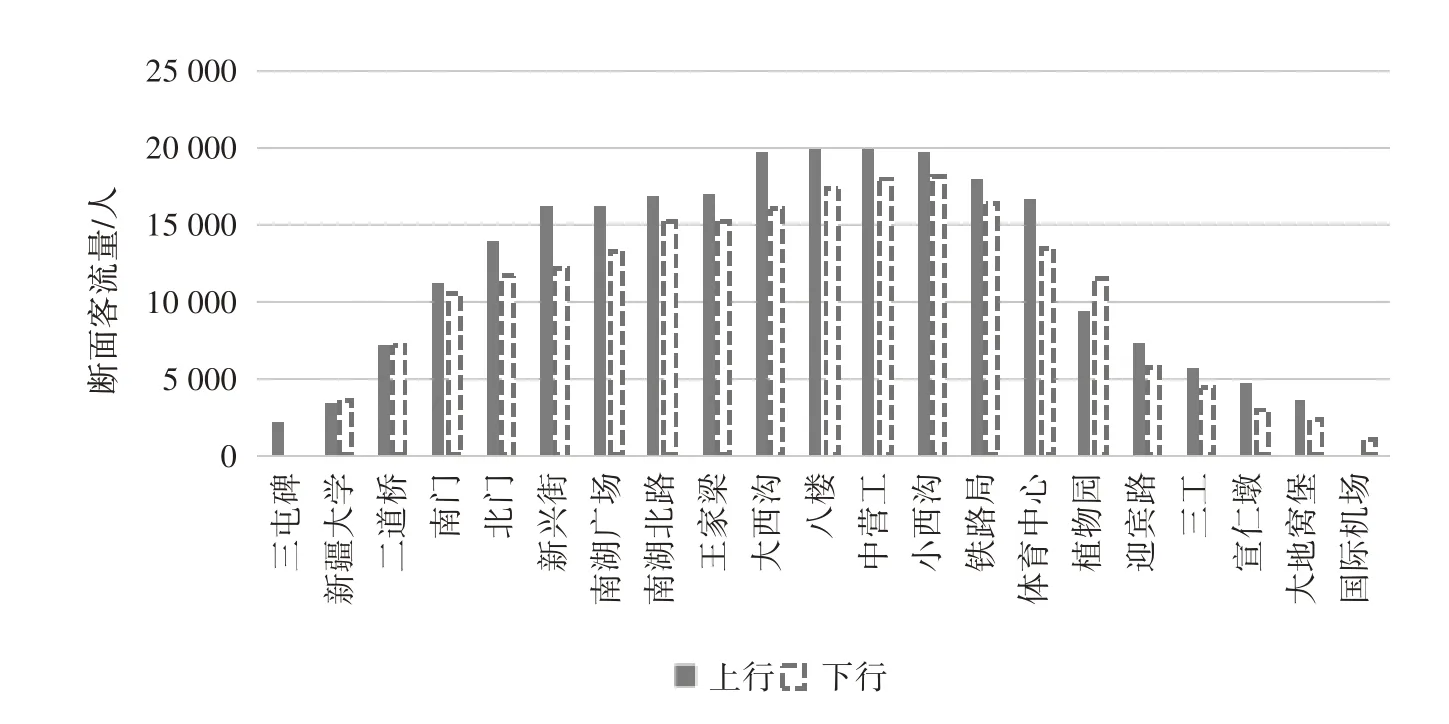
图6 晚高峰断面流量

4.2 计算结果与分析

对模型求解，经计算可得，在β=1.2 的前提下，a=1、b=17时得到最优解，对应折返站为三屯碑站和三工站。大交路运用列车数为18，小交路运用列车数为9，如表1所示。

由表1 可知，大小交路开行方案最优。早高峰段，当开行比例为2∶1（大交路区段开行对数为18、小交路为9）时，乘客出行时间总体延长，乘客出行成本增加，企业运营成本降低，早高峰乘客出行成本增加5.2%，企业运营成本降低7%，总成本降低3%；晚高峰段，大小交路开行比例为2∶1（即大交路区段开行对数为16、小交路为8）时，乘客出行时间总体延长，出行成本增加7%，企业运营成本降低7%，总成本降低2.5%。

表1 求解结果

5 结语

本研究从运营成本与乘客出行成本两个方面出发，建立双目标非线性函数模型，并设计求解算法。结果表明，基于双目标非线性函数模型设计出的算法可实现城市轨道交通大小交路模式列车开行方案的有效求解与优化。在一定条件下，城市轨道交通实施大小交路模式，可降低总体成本。在特定客流、线路参数情况下，实施大小交路运营模式，会增加乘客出行成本，但能降低企业运营成本。在大小交路运营模式下，考虑如何降低乘客出行成本是下一步重点研究的内容。