民航机场运动目标实时运动仿真①
2022-11-07宋云雪
宋云雪,张 颖
(中国民航大学 航空工程学院,天津 300300)
1 引言
现阶段国内外学者对机场地面保障研究大多集中在机场地面保障流程优化[1-3],机场保障能力验证评估[4,5],机场运输决策[6,7]等方面,针对上述文献进行总结分析,由于机场环境的特殊性、机场信息的离散性和复杂性,现有部分保障流程优化研究难以对方案和研究方法进行实地应用验证; 而对机场保障能力评估时多数学者缺乏真实详细的机场方案实施数据,结果具有一定的主观性; 在机场运输决策等领域需要大量机场实时监测信息,信息的匮乏和机场试验的局限性会导致研究方法和方案的可行性难以判别.对于机场运动仿真研究,Alomar 等人基于FlexSim 构建机场地面车辆移动仿真模型来优化其在运动过程中的运输流程[8],潘卫军等人基于Unity 对机场应急演练过程进行了仿真评价[9]; 分析国内外现有机场仿真研究多数借助了需要付费的第三方平台仿真引擎软件,建立的仿真模型使用受平台限制难以迁移,开发的程序缺乏复用性,软件学习和使用复杂度较高.本文为解决上述问题,独立设计并开发了一种机场运动目标仿真模型,借助计算机仿真技术对机场地面保障过程进行仿真,构建的模拟环境为机场保障中设施分配、路线规划等流程优化提供验证环境; 对机场旅客、行人、保障车辆和航空器运输工具等目标进行运动仿真,能复现机场各部门组织工作状态和机场保障设备的作业情况,产生的数据可为机场保障预案和保障能力评估验证提供依据; 仿真模型的真实地理环境数据和机场目标实时位置数据可为机场应急处理、运输决策等提供判断依据;同时机场保障过程仿真也是基于民航安全无误原则下对人员进行培训的有效方法,可以为民航从业人员提供指导思路.此外,本研究设计实现的仿真模型可独立运行,也可嵌入机场保障相关的复杂系统,应用于民航机场研究相关的多个领域,具有广泛的适用性,对提高机场航班过站保障能力具有重要意义.
2 底层数据模型构建与实现
2.1 数据存储关联模型构建
实现底层数据的存储和关联是构建机场地面目标仿真模型的基础.机场地面保障全过程基于机场复杂的内部环境,而GIS 图层的要素、表面和模型能够构建模拟不同机场的环境地形.Xu 等人基于C#程序和ArcObjects 提出了一种数字地图瓦片编码和计算方法,生成的瓦片地图可供在线和离线应用程序使用[10].本文在文献[10]研究基础之上,借助GIS 开发平台生成机场瓦片地图为仿真提供环境数据.
由于涉及的机场瓦片数据体量和数量巨大,离线环境下如何对其进行合理存储和有效管理是面临的一大挑战.近年来Zhang 等人提出了一种基于Hadoop 的分布式文件系统栅格瓦片存储策略[11],Lv等人提出了一种基于嵌入式数据库的海量地图瓦片存储技术[12].基于上述研究,结合分布式文件系统和数据库存储特点,本文采用分布式文件系统和关系数据库相结合的方式来管理机场瓦片地图数据: 构建共享目录树将不同机场瓦片地图和拼接图存储在多个服务器,用户访问单个路径结点就能读取到所需机场卫星瓦片地图资源; 使用关系数据库存储城市基础信息、机场点数据层和道路设施分布层等标注信息,机场运动目标仿真底层关联数据模型如图1 所示.
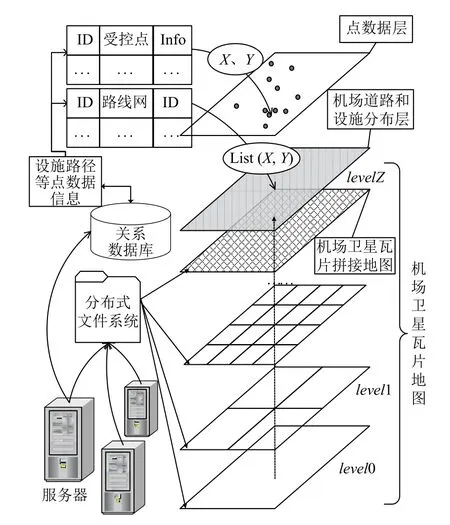
图1 仿真底层数据关联模型
图1 中点数据层的机场受控点和分布点标注功能基于.Net 的GDI+实现,底层数据关联图中点数据层的坐标系使用GDI+的页面坐标系,该坐标系原点位于仿真绘图窗口左上角.如图2 为南宁吴圩国际机场的道路及设施分布层页面,在该层标注了机场的关键设施以及机场运动目标行驶部分路线网络.

图2 南宁吴圩国际机场设施道路分布层
2.2 地图层级关系
机场目标运动仿真过程要得到真实的地理数据测算结果,需要实际环境和仿真环境比例关系,即表示地图上一个像素坐标点所代表地球上实际距离长度的地面分辨率参数.结合图1 中数据关联模型,根据选定的机场瓦片地图层级计算地图分辨率,图1 中机场卫星地图各层每个切片统一为256×256像素,level0对应单个瓦片,level1对应4 个瓦片,以此类推,得到levelZ的机场地图瓦片个数CountlevelZ为:
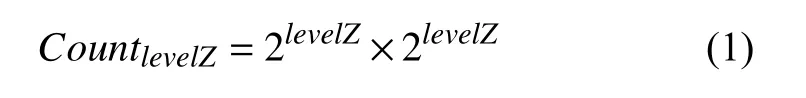
机场瓦片地图采取Web 墨卡托投影坐标系,设赤道半径为Re,其坐标系范围X方向最大值为Maxx,拼接地图对应的瓦片地图层级为levelZ,瓦片数量为CountlevelZ,各级瓦片拼接图总像素宽度为WidthlevelZ,levelZ级机场卫星地图的地面分辨率为GRlevelZ,单个瓦片的像素宽度为Width,由式(2)和式(3)得到式(4)地面分辨率GRlevelZ,公式如下:
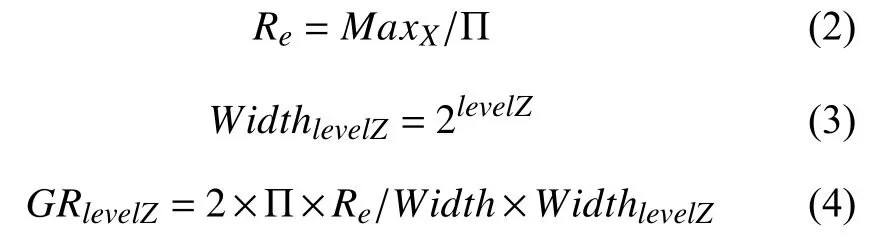
为了保证仿真效果的清晰度和良好的用户体验,仿真模型中的底层机场瓦片数据默认为16-18 级的瓦片地图拼接图,各级机场拼接地图对应的切片个数CountlevelZ和地面分辨率GRlevelZ计算结果如表1 所示.

表1 机场地图层级关系对应表
研究以天津滨海国际机场的18 级瓦片拼接图为例,在机场点数据层标注编号TJ01 的跑道坐标4 点分别为(1842,1318)、(1930,1275)、(3902,5619)、(3993,5577),该跑道内移坐标点为(2095,1850)、(2185,1807)结合地图层级关系对应表,可计算出天津滨海国际机场西跑道可用着陆距离(LDA)约为2 500 m,可用起飞距离(TODA)约为2 850 m 等数据,为后续机场地面保障仿真过程计算奠定基础.
3 运动数学模型构建与实现
3.1 坐标复合全局转换
机场地面目标在绘图平面上的交互基础是对模型所在坐标系和仿真展示页面坐标系进行坐标转换.针对坐标系平移,通过仿射变换增加矩阵维数,将二维矩阵表示形式转换为三维矩阵,使用三维矩阵左乘的方式实现运动目标所在坐标系和仿真绘图平面坐标系的平移、旋转和缩放.以图3 飞机为例,把目标运动坐标系中飞机模型放置在绘图界面坐标系中.

图3 运动目标坐标系与绘图坐标系转换
首先针对机场绘图界面坐标系XOY在 X轴方向上平滑移动m个单位,Y轴方向平移n个单位,设平移变换的系数矩阵为M1; 再对XOY绘图界面坐标系Y 轴反向缩放,缩放变换的系数矩阵为M2将经上述矩阵变换后的绘图界面坐标系旋转顺时针旋转θ度,旋转系数矩阵M3; 最后通过计算绘图界面坐标系与运动目标坐标系的像素比例关系为1:f进行缩放,系数矩阵为M4,那么图3 的转换过程可以表示为:
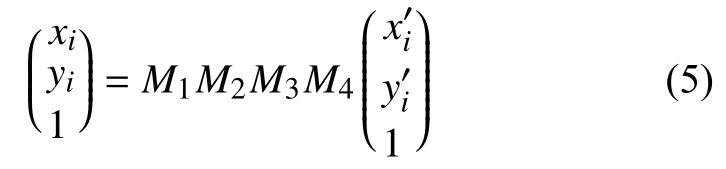
结合矩阵复合转换方式,将M1M2M3M4四个矩阵相乘表示为单个矩阵M,通过计算M可表示为:
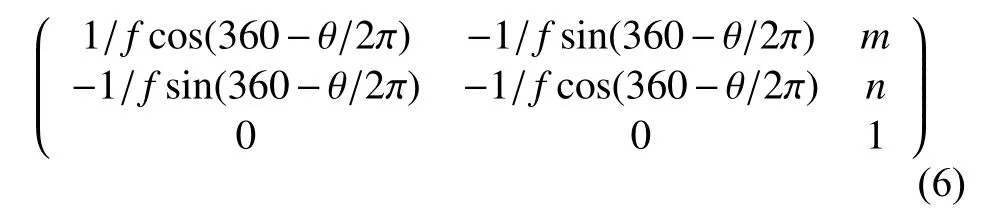
结合矩阵式(5)、式(6)运算,在已知运动目标坐标系中运动模型某点坐标情况下可计算出该点在绘图界面坐标系中的坐标.结合GDI+坐标全局转换设计程序实现运动目标在仿真界面坐标系中的绘图操作,如图4为飞机在机场某时刻降落滑行的运动状态.

图4 仿真界面飞机运动目标滑行过程
3.2 运动目标最短路径
机场运动目标在机场路网运动行驶前需要确定移动路径,本文对A*算法加以改进,利用改进的A*算法来确定机场运动目标的最佳行驶路径.A*算法是一种启发式搜索算法,它的计算效率相比与Dijkstra 算法更快,利用其估价函数对节点加以扩展能够找到最合适的目标节点; 利用A*算法求解最佳路线过程中,虽然搜索节点明显少于Dijkstra 算法,但其在大规模路网条件下搜索节点数量依旧会影响计算性能.本文对机场分区处理,将各区域路径坐标点进行区域编号; 通过分区预处理操作对各区域运动目标行驶路线范围加以限制达到A*算法在预处理环节减少搜索节点的目的.其中机场路网的点坐标信息存储结构如表2 所示.

表2 机场路网点坐标信息
A*算法的节点a估价函数如式(7):
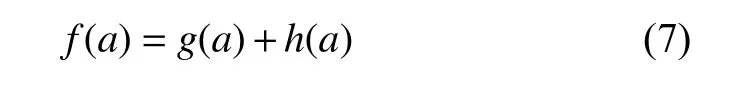
其中,g(a)是从机场运动目标的设定运动起点到点a的实际成本,h(a)是节点a到目标节点的最优路径估计成本,启发式函数h(a)的设计是A*算法的关键.分析机场路网特点,排除同一种类的机场目标同一时间段超速现象,机场的机场运动目标行驶路线网络满足时变网络的先入先出条件(FIFO),也就是同一时段同种类机场运动目标先出发的比后出发的先到达.设机场运动目标给定出发时刻为Tstart,起点Vstart,终点为Vend,所有点坐标集合为Vlist,坐标连接的路段集合为Alist,现有未找到的运动目标最佳路径剩余节点集合为NFlist,节点a的编号为Na,它的前驱节点为FNa,Tab(t)是机场运动目标t(t∈T)时刻在ab路段的出发时间,T是机场运动目标完成运动过程的总时间分段集合.对于任意(a,b)∈Alist,(t)=minTab(t),用(t)构造静态网络G,tmin(a,b)表示机场运动目标在G中从a点到b点的最短路径的行程时间.对启发式函数h(a)定义如下:
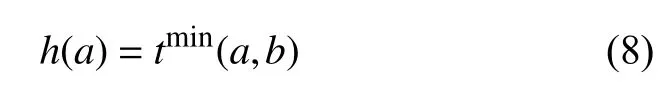
根究式(7)、式(8)设计改进的A*算法计算流程如下:
(1)利用数据库分组筛选出与当前机场目标所在点区域编号相邻的点坐标集合Plist;
(2)采用Dijkstra 算法计算集合Plist中点坐标到目标节点的h(a);
(3)初始化变量Va,Ta且对于变量∀b≠a,Tb=+∞,FNa=0,Slist={Va},NFlist=Φ.
(4)改变节点编号,对所有a的后继节点,如果Tb>Ta+Tab(Ta)+h(a),则Tb=Ta+Tab(Ta)+h(a),FNb=FNa若b∉NFlist,则NFlist=NFlist∪{b}.
(5)选择节点,设Vmin=min(b),b∈NFlist,令Va=Vmin,则Flist=Flist∪{a},NFlist=NFlist-{b}.
(6)如果Va=Vend,停止计算,否则回转到步骤(1).
(7)通过反向追踪节点a的前驱节点FNa,得到最短路径.
通过改进的A*算法,可以在仿真过程中提前对机场运动目标运动最佳路线进行规划,提高机场运动目标作业效率.
3.3 仿真过程数据可视化
GDI+的原始画图模式采用了Graphics 接口,该方法画图效率缓慢,而且在仿真测试过程中出现了严重的闪烁效果.在对图像处理过程中很多学者采用缓冲技术提高图像处理效率,如Zhou 等人研究了一种实时固定比例帧缓冲压缩技术应用于嵌入式图形系统中[13];王宇飞等人利用双缓冲技术显著提高了测井曲线的绘制速度[14]; 为了避免绘图效率对机场地面运动目标仿真过程的时效性造成不必要的干扰,影响仿真的准确度,本文采用GDI+自带的双缓冲类BufferedGraphicsContext实现双缓冲画图模式,较大程度上减少了程序绘图运行速度对仿真实时性的影响.
基于实时仿真理论,要将运动目标移动状态与具体时间相关联,在坐标变换绘图过程中,模型的移动距离需要随时间变化而做出调整.利用GDI+技术调整绘图瞬间对应的坐标点位置,以目标运动过程总时间划分合适的单位时间步长T,结合单位时间内的速度变化和运动目标朝向角度变化值,计算单位时间步长T时段内X轴和 Y轴方向的位移增量,进而计算确定绘图坐标点位置.排除了绘图效率对仿真模型中绘图过程的客观影响,并结合模型中机场目标运动路径的存储结构和运动规律,对确定绘图坐标点的实际问题建立计算模型.
图5 左边绘图坐标系中是机场运动目标移动行驶路线网络,其中摆渡车路线01 是利用改进的A*算法求解确定的摆渡车最佳行驶路线,以该条路线为例,将路线中已知的相邻坐标两点分解放大,已知机场运动目标模型对应的行驶移动路径、运动速度、运动加速度和运动时间等信息,每隔单位步长T,确定绘图对应坐标Pn的位置计算模型如图5 所示.
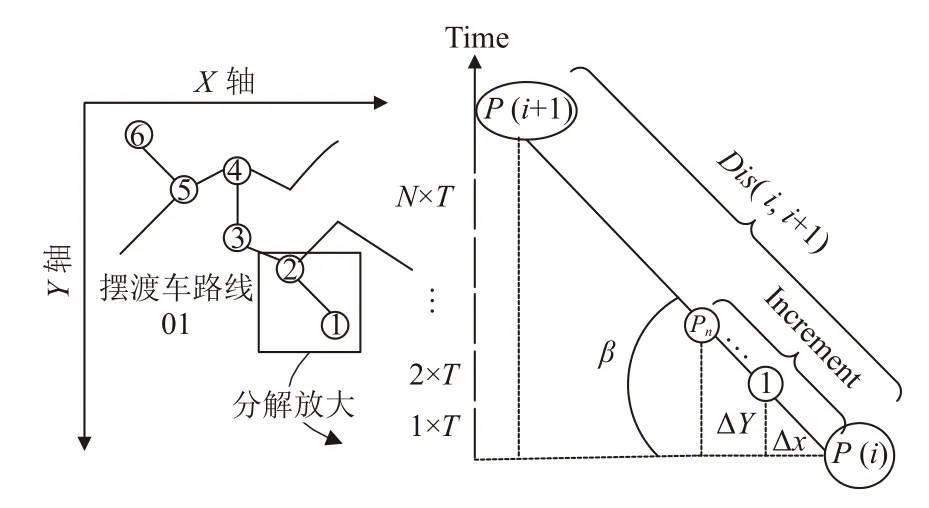
图5 路线相邻路径点分解计算模型
为方便机场运动目标属性的描述与其相关数据的合理存储,为机场运动目标建立统一的数据模型Model,如表3 所示.

表3 运动目标模型Model 属性
令路径中已知坐标点为P(i),其相邻坐标点为P(i+1),两点之间距离为Dis(i,i+1),两点之间连线与水平方向夹角为 β,单位时间T间隔内 X方向和 Y方向增量分别为 Δx,Δy,N个T时间间隔内的模型位移增量为incrementNT,结合表3 中Model 的相关属性数据描述,对目标模型匀速和非匀速运动过程绘图坐标点Pn求解流程梳理如图6 所示.
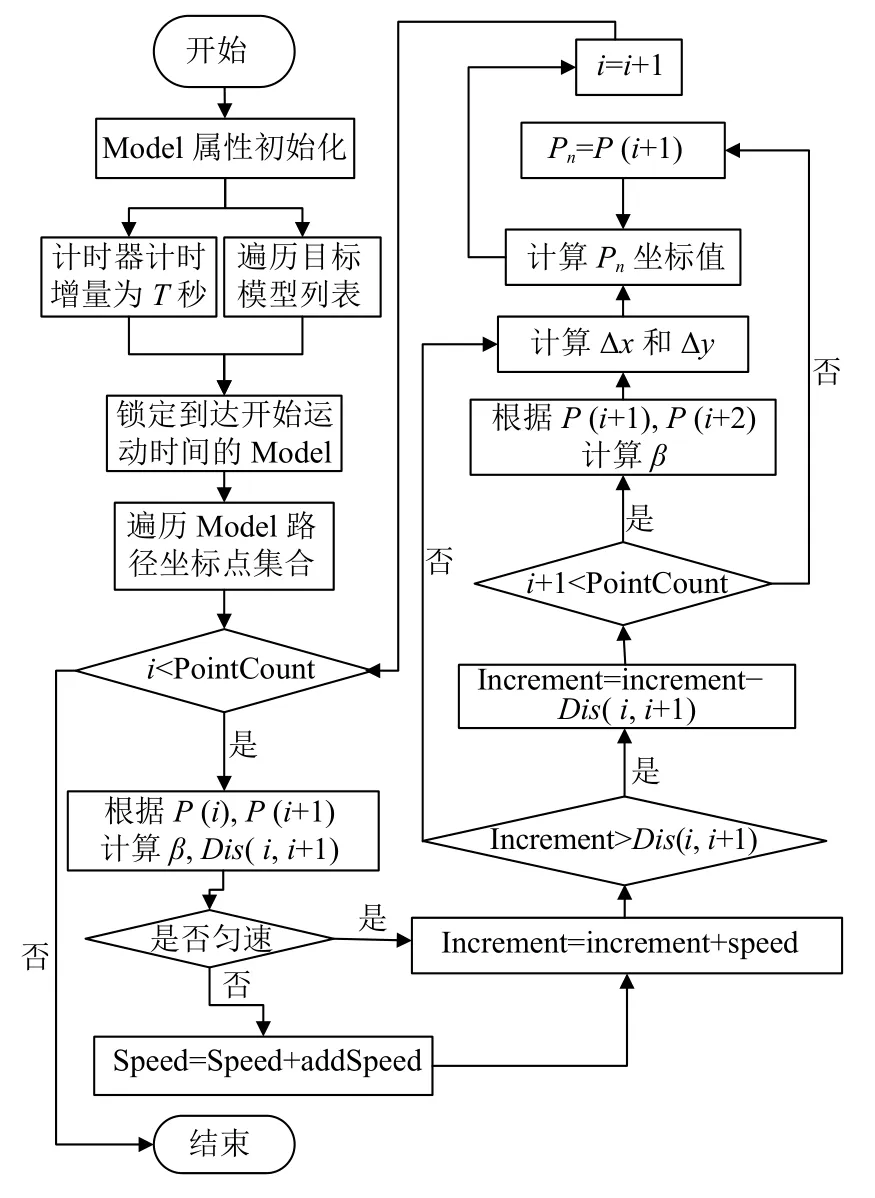
图6 目标模型绘图坐标点求解流程图
基于上述计算模型,本文采用面向对象的程序设计方式,设计Model 类封装其相关属性,初始化构造函数,移动距离、运动速度、旋转角度等计算函数,模型旋转角度计算方法主要功能是以对象绑定的移动路径已知坐标点为基础,计算目标在运动目标坐标系到绘图仿真界面坐标系绘图操作时的旋转角度circle_angle(i,i+1),结合GDI+绘图仿真坐标系特点,该角度值主要包括以下4 种情况:
(1)当yP(i+1)>yP(i)时:
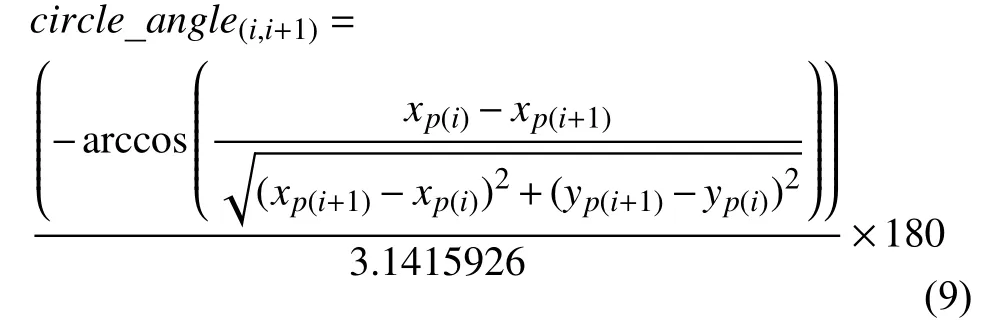
(2)当yP(i+1)<yP(i)时:
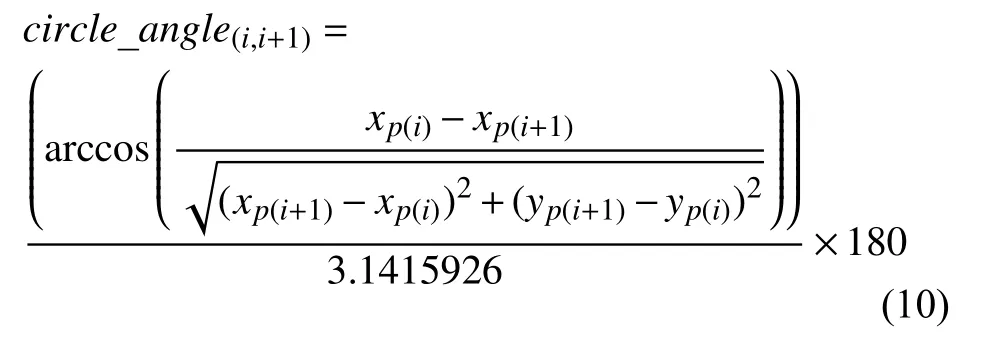
(3)当yP(i+1)=yP(i)且xP(i+1)≥xP(i)时:
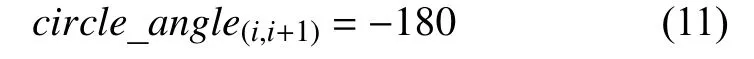
(4)除上述情况外,旋转角度值为:

综合式(9)-式(12)可在已知模型路径点坐标条件下正确控制仿真过程中机场运动目标的运动朝向角度.根据 X轴和 Y轴方向上的位移增量,在确定单位步长时间段内对应的绘图坐标点Pn时也包括了多种情况,如表4 所示.

表4 不同条件下 Pn坐 标值
结合坐标计算流程图对相关数学理论模型,编写程序接口将机场地面目标实时运动仿真过程产生的数据可视化,以天津滨海国际机场某航班地面保障摆渡车行驶运动过程为例,该运动目标仿真过程的实时坐标位置、运动速度、朝向角度等数据展示如图7 所示.其中详细的轨迹坐标和对应位置的时刻信息可以为运动目标行驶路线碰撞检测评估提供数据支撑,运动目标的速度位移变化可以用来评判目标从出发地到目的地的运动可行性.
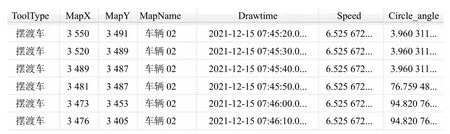
图7 Model 运动仿真过程数据可视化
4 仿真过程的并发改进设计
4.1 传统定时器管理多线程任务
机场运动目标实时运动二维仿真过程实际上是结合具体时间不断实现图像绘制和数据计算的同步过程.机场地面运动目标运动过程仿真涉及到的地面保障车辆、旅客、保障人员、各类航空器的运动过程对应多个时间阶段,而每个时间阶段也可能包括多个目标同时运动的过程,如图8 截取的某机场部分地面保障环节涉及到多个机场运动目标进行作业,根据机场地面目标运动特点,设计并发程序将仿真各个阶段任务合理分工交给多个线程完成.
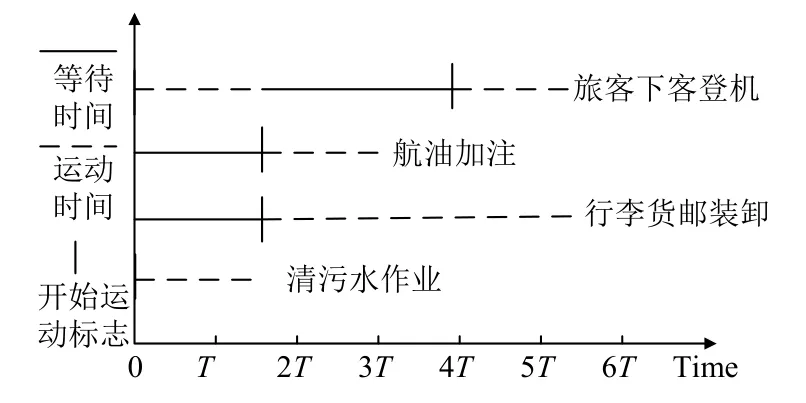
图8 机场保障部分作业流程
本文采用多线程技术,利用计时器来控制和管理不同时间阶段对应的多线程任务,System.Timers.Timer 是.Net 基于服务器的多线程计时器,可以按照设定的时间间隔执行事件处理程序,非常适合机场保障过程中不同目标按照固定时间间隔执行任务的情景,直接使用该计时器管理仿真计算过程流程如图9所示.
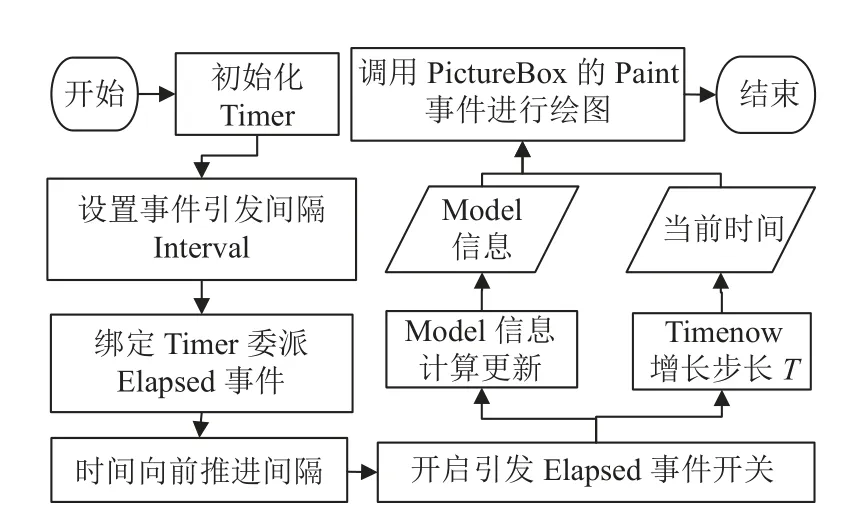
图9 多线程仿真绘图流程
在计时器管理多线程任务过程中,如果一个计时器对象绑定的Elapsed 事件函数没有处理完成,到达下一个时间点新的线程依旧会按时启动执行Model 信息更新的回调事件,当遇到回调事件计算耗时而方法未在设置的interval 间隔内执行完毕的情况下,很容易出现超时导致的多线程重入问题,也就是多个线程进入了计时器对象绑定的Elapsed 事件,导致线程不安全.图10 是按照上述流程某罐式加油车的仿真实时坐标更新情况,设置事件引发间隔为100 ms,到达间隔引发事件: 时间轴增长步长T秒,Model 信息计算更新; Timer不管回调事件是否执行完毕,它只负责每隔100 ms 触发一次,由于系统处理效率存在不稳定性,出现了部分线程未在规定时间范围内完成数据计算情况,由此引发多线程重入问题导致坐标重复更新.

图10 改进前目标位置更新时间表
4.2 仿真过程并发改进
本文对上述仿真绘图流程加以改进,让定时器定时引发的回调事件能够阻塞执行,并且能够动态的添加和移除多个不同机场目标定时运动任务.
基于锁的同步机制是多线程并行应用中同步操作的主要实现机制[15].可重入锁可解决多线程重入导致的线程不安全问题,但是考虑到本文频繁调用回调事件,简单的对回调函数部分进行加锁操作会严重影响仿真性能,本文对于单个机场运动目标仿真过程,结合回调次数来阻塞定时器达到线程安全的目的.首先对计时器进行类封装,在封装类中对计时器调用时先将计时器阻塞,设置函数回调次数为单次保证回调函数线程安全,回调事件执行完毕后再对计时器重启.通过上述操作能够定时阻塞调用回调方法并且很大程度上提高了仿真性能,并保证了单个运动目标的线程安全性.
考虑到机场地面保障作业任务的多目标多时段等特点,要实现多个机场运动目标的多个定时任务仿真过程正常运行,设计静态类SimulateTimerTask 实现多个不同机场目标不同时段的定时运动任务.该封装类主要包括以下函数属性如表5.
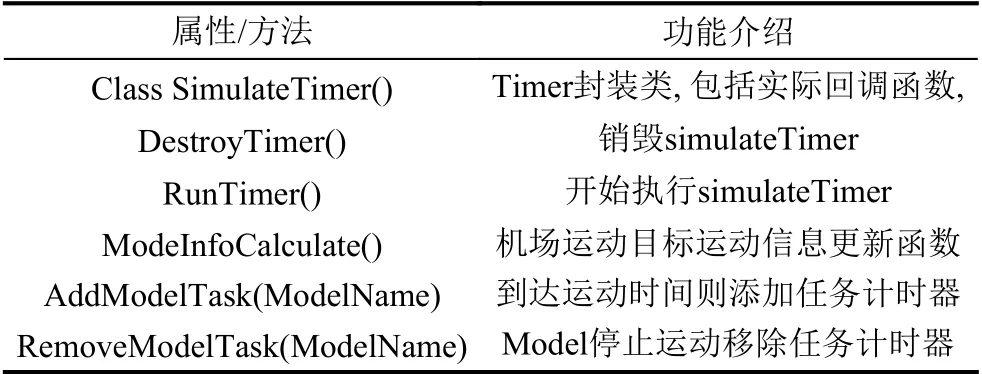
表5 SimulateTimerTask 类关键属性函数
为了在添加和移除不同机场运动目标的定时作业任务时保证线程的安全问题,在类内部通过字典管理所有的SimulateTimer,同一个Model 的定时任务在添加时只会增加SimulateTimer 的调用次数,而不会再次实例化新的计时器封装对象,在添加和移除定时任务函数中使用锁机制保证线程安全,添加机场运动目标定时任务部分伪代码如下:

readonly object dicLock;Dictionary<Modelname,SimulateTimer> timerDic;AddModelTask(ModelName){lock (dicLock){if (timerDic != null)isCreateTimer = true;if (timerDic.ContainsKey(ModelName)){SimulateTimer tarTimer = timerDic[ModelName];tarTimer.callCount++;isCreateTimer = false;}if (isCreateTimer){timerDic.Remove(ModelName);newTimer = new SimulateTimer(ModelName);newTimer.timerCallBack += Timercallback;newTimer.callCount = 1;timerDic.Add(newTimer);newTimer.RunTimer();}}
对程序改进后的某罐式加油车的仿真实时坐标更新情况如所示,图11 与图10 改进前的结果比较,对仿真过程的并发改进设计有效解决了多线程重入导致的线程安全问题,提升了仿真程序性能和线程执行任务的准确性.

图11 改进后目标位置更新时间表
对仿真过程进行总体实现,某机场在特定时间段保障车辆行驶过程、飞机滑行过程、人员轨迹绘制等实时二维仿真效果如图12、图13 所示,界面下方时间轴记录当前具体时间变化,动画仿真窗口展示对应时刻的机场地面目标实时运动状态.

图12 机场运动目标实时运动仿真过程展示

图13 机场运动目标实时运动仿真过程展示
5 仿真试验结果分析
本文利用复演法对建立的仿真系统模型进行终态仿真试验,机场运动目标每次仿真运行都是相互独立的,采用相同的初始条件和相同的目标运动参数对系统模型进行N次仿真,设每次仿真运行结果Xi是服从正态分布的随机变量,随机变量X的期望E(X)为:

其中,
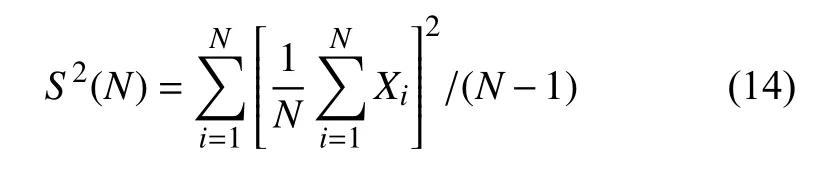
制定试验方案,以天津滨海国际机场某时段地面保障过程运动仿真为例,设定多次试验以相同速度、时间间隔和相同路径距离进行仿真模拟.明确仿真初始状态后定义多个定时任务,对上述运动过程重复运行程序监测采样50-80 次,为避免每次试验仿真运行速度对结果产生影响,将所有试验方案的仿真运行速度统一设置为100 ms/步长; 记录不同地图级别和不同仿真步长对应的横纵坐标变化像素值、运行时间、仿真轨迹坐标等数据,结合式(13)和式(14),对仿真误差百分比和仿真效率进行分析计算,根据试验采样数据计算结果生成统计分析图,如图14、图15 所示,图中第1-8、9-17、18-24 组数据分别从左到右对应机场瓦片地图的层级数为16、17、18 级,仿真结果详细分析如下.
使用本文研究的仿真模型系统进行上述试验,如图14 为多次试验采样中16-18 级瓦片拼接地图不同仿真步长情况下的误差距离与上述仿真实验路径总距离的比值,结果显示在1-14 s 步长范围内误差值控制在0.50%以下,随着地图级别增加,仿真误差逐步减小; 图15 是不同地图层级在不同仿真步长范围的仿真绘图程序运行时间数值变化情况,随着仿真步长增大,运行时间相对减少,程序运行效率随之提高; 结合仿真动画中目标运动轨迹连续性及误差比值、程序运行时间等多个因素,从实验结果和数据分析图中可总结出: 将仿真步长设定在4-10 s 范围内不仅能够取得良好的动画效果且能将误差控制在较小范围内,在地图层级数较低情况下可适当降低仿真步长,层级较高情况下可适当增加仿真步长来改善仿真效果和程序运行效率.
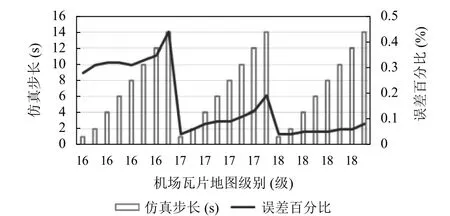
图14 多个定时任务下不同仿真步长误差占比趋势
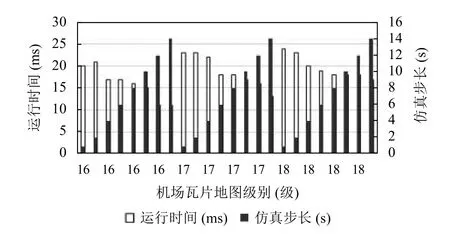
图15 多个定时任务下不同步长仿真过程运行时间
6 总结
本文对机场运动目标运动仿真过程进行数学建模,利用改进的A*算法确定机场运动目标行驶路径,结合并发机制对仿真过程进行改进,针对具体的仿真试验对仿真结果进行统计分析,最终实现了一种机场地面目标实时运动仿真过程模型,具有形象、安全、经济、实效等特点.该仿真模型现可应用于机场地面保障流程推演,应急方案验证、运输决策等多个领域,充分体现了四型机场的“平安、绿色,智慧、人文”核心思想.
