储能逆变器H∞鲁棒跟踪控制
2022-11-06孙树敏王士柏王玥娇
于 芃,孙树敏,程 艳,王士柏,王玥娇
(国网山东省电力公司电力科学研究院,山东 济南 250003)
0 引言
近年来,在我国电力系统中,以光伏风能等为代表的新能源发电装机增长猛烈,因此须对电网供电台区中储能系统、电动充电桩以及用户可移动负荷等对象进行协同控制[1]。同时,由于各类储能装置输出为直流电,需要电力电子器件的逆变才可满足在台区的稳定运行或并入交流大电网。由于供电台区结构及运行方式复杂,逆变器需具有多种控制策略才能满足电压、频率各项指标的平稳运行。几种控制策略中,功率控制模式控制中分布式电源一般无法给供电台区系统提供可靠的电压支撑,电压频率控制模式控制外特性较差,一般在孤岛状态下工作[2-3]。
国内外学者提出了基于下垂控制的虚拟同步发电技术控制策略[4],通过下垂控制模拟传统同步发电机静态特性,使得各储能单元输出功率实现合理分配,模拟了同步发电机的机械方程,使电网具有惯性和阻尼。文献[5]提出了一种考虑线路阻抗效应的分布式交流电力系统并联逆变器控制,不需要控制互连,并自动补偿逆变器参数变化和线路阻抗不平衡。文献[6]在基于逆变器输出阻抗的基础上,进行了电压电流多环反馈控制器的设计,但该方法只能用于理想情况下输出阻抗为感性时。
在电力系统中,各类电力装置负荷时间常数不同,响应不同。当扰动发生时,系统同时存在微秒级别震荡的电磁暂态过程,亦存在毫秒级别快速变化的机电暂态响应。这就导致了系统抗扰动能力较弱[7-8]。文献[9]提出了一种相位超前补偿的方法来补偿电感电流反馈的延时,分析了不同谐振频率下系统的响应。此时,传统下垂策略中基于坐标系解耦的比例-积分控制策略以及自适应调节无法应对系统扰动的快速变化。运用现代鲁棒控制理论,当系统存在外界较大扰动或参数摄动时,基于系统模型可以设计出具有良好抗扰效果的鲁棒控制器[10-11]。
文献[12]构建了一种混合灵敏度函数,用以提高微电网抗击直流和交流扰动的能力,文献[13-14]提出了一种基于混合灵敏度来控制交直流混合微网系统中频率的控制策略,构建回路灵敏度函数,利用线性矩阵不等式求解Riccati 方程得到频率控制器,增强了频率对参数摄动的鲁棒性。
在现有研究的基础上,提出了一种用于储能逆变器虚拟同步发电机(Virtual Synchronous Generator,VSG)控制中对电压H∞鲁棒控制方法,解决了负载突变与滤波器参数变化降低电压质量的问题。相较于常规的电压电流双闭环比例-积分控制或下垂控制,跟踪系统电压能力、抗干扰能力更强。首先在传统VSG控制合成参考电压后,建立系统结构的机理模型,同时对扫频输入到正弦波脉宽调制调制器产生的逆变器输出信号进行采集辨识得到系统的辨识模型,二者比较后,将外界干扰和建模误差作为不确定性函数建立H∞鲁棒控制器对参考电压进行跟踪,增加了系统抗干扰性能,并通过MATLAB/Simulink搭建逆变器闭环控制模型,验证了所提出控制策略的有效性。
1 储能逆变器主电路系统设计
1.1 虚拟同步发电技术原理
虚拟同步发电机中的下垂控制即模拟同步发电机有功功率与频率的关系(功频特性)和无功功率与电压的关系(励磁特性)。图1 所示为储能逆变器下垂特性曲线,包括功频特性曲线和励磁特性曲线。

图1 下垂特性曲线
由图1 可以推出,由逆变器功率下垂特性可以推出,传统的下垂控制数学表达式为:

式中:fn为电网额定频率,一般为50 Hz;Un为电网参考电压幅值;f、U为下垂控制器输出参考值;M、N分别为有功、无功下垂系数;Pref、Qref为额定参考功率。
虚拟同步发电技术在下垂调节有功-频率环中模拟了同步发电机的机械特性,即
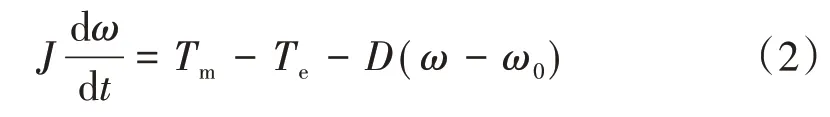
式中:J为同步发电机转动惯量;Tm为机械转矩;Te为电磁转矩;D为阻尼系数;ω0为电网额定角速度;ω为实际输出电压角速度。
储能逆变器中引入转动惯量和阻尼使系统的频率支撑更可靠,对频率震荡有较强抑制作用,能够更快过渡暂态过程[15],同时又可以不受同步发电机中定子和转子等物理结构的限制,具有更宽的运行范围和动态性能。
1.2 储能逆变器主电路结构
在供电台区中,多个分布式电源或储能系统经逆变器等电力电子装置高质量地向各类负荷供电,经过继电器、变压器等配电装置与配电网络相连接。在本文中,将其中一个分布式电源构成的局域台区用逆变器控制电路进行等效研究,假设直流侧电压源Udc为常数,维持不变。
基于电压鲁棒控制的储能逆变器原理如图2 所示,主要包括:直流电源代替分布式电源提供直流电;三相电压源逆变器将直流电转为三相交流电;电感-电容滤波电路将逆变器输出的方波转化为符合电能质量要求的三相正弦波以及控制器部分,控制器部分包括VSG 调节环节,电压合成环节和鲁棒控制器。
根据直流侧电源性质的不同,逆变电路可分为两种形式:电流源型逆变器和电压源型逆变器,本文主要采用三相全桥电压源型逆变器。
图2 中,Udc为直流侧电压;S1—S6为逆变器开关管;L、C分别为滤波器的滤波电感、电容,为避免电感-电容滤波器震荡,在电容处并联一个小电阻R;ea、eb、ec为逆变器输出相电压;iLa、iLb、iLc为VSG 输出电感电流;Uabc为VSG 输出电容电压;Iabc为逆变器输出电流;为VSG算法输出参考电压。

图2 系统整体控制原理
利用电压电流传感器采集到的输出电压Uabc和输出电流Iabc,在三相静止坐标系计算得到瞬时有功功率P和瞬时无功功率Q后转为dq坐标系下的功率关系式分别为:

式中:Ud、Uq为dq坐标系下的输出电压;Id、Iq为dq坐标系下的输出电压[16]。
综上所述,可以得到基于H∞鲁棒控制的储能下垂逆变器的基本流程为:传感器采集输出电流Iabc和电压Uabc,经过功率计算得到输出瞬时功率,加入后低通滤波器得到平均有功功率和无功功率。通过VSG 控制环节得到频率指令值和电压幅值参考值,对频率对应的角速度进行积分得到电压相位角,由此合成了三相对称的参考电压Uref,经过park 变换从三相坐标系转为dq坐标系后,将其输入到鲁棒控制模块中得到参考信号,再经过正弦脉宽调制技术(Sinusoidal Pulse Width Modulation,SPWM)得到脉冲驱动信号控制逆变器中开关管的通断,从而控制逆变单元的输出电压。
1.3 系统数学模型的建立
在电力系统中,储能单元、逆变器、滤波器等环节本身包含了大量非线性元件,如二极管、开关管等。所以整个系统本质上可以当作一个非线性且离散的系统。工程上常采用平均开关模型法来得到系统的数学模型,其原理是将一个开关周期内的瞬时值用平均值代替。
根据基尔霍夫定律,建立逆变器在三相静止坐标系下的数学模型,表达式为:
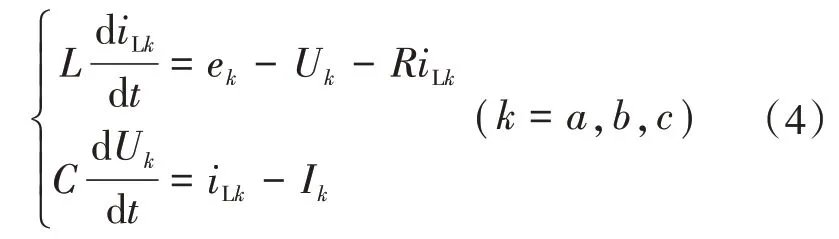
式中:Ua、Ub、Uc为逆变器输出电容电压;Ia、Ib、Ic为负载公共连接点的电流。
实际工程应用中,由于SPWM 控制逆变器开关管其状态不连续,假设开关器件的频率远大于基波输出电压的频率,我们常使用状态空间平均模型法得到逆变电路控制模型。
假设逆变器带三相对称阻性负载,则由式(4)可推得逆变桥输出电压UkN与公共连接点电压即负载电压Uk的传递函数为
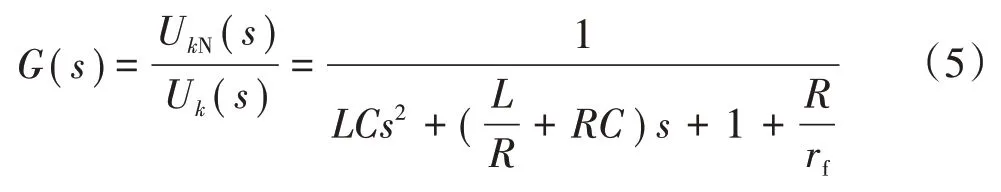
式中:rf为负载电阻。
对于SPWM 调制的三相逆变器,当考虑主电路的延时,逆变器则可当作一个滞后环节,忽略高次项,其简化后的滞后环节传递函数为

式中:KPWM为逆变器比例系数。根据SPWM 调制原理,当载波信号频率fc远大于调制波信号频率f时有

式中:Ulm为逆变桥输出基波幅值;mlm为调制比。
由式(5)—式(7)可推得逆变电路从SPWM 调制器输入到输出负载电压的传递函数为

以上分析均是基于系统结构建立的机理模型。然而,由于系统的建模误差,以及各环节存在的参数不确定性如有功功率和无功功率的耦合,进而导致数学模型推算复杂。故本文采取了基于系统运行和实验数据辨识得到的模型。
为了对电压源逆变器组成的逆变电路的动态性能进行分析和控制,首先要得到逆变电路的动态特性的数学模型,以三路扫频信号作为SPWM 的调制信号,对电压源逆变器进行充分的激励,从而得到相应的频率响应,根据频率响应辨识可得逆变电路的数学模型。
以三路扫频信号作为SPWM 的调制信号,采集逆变器经过滤波器后输出的一路电容电压如图3所示。
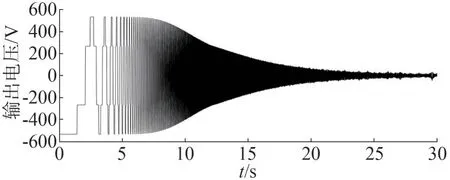
图3 输出响应曲线
由于开始输入扫频信号的频率很小,远小于滤波器的截止频率,故输出电压波形开始时依旧为方波,随着频率的上升逐渐变为正弦波[17]。
将采集到的时域中的输入输出电压信号通过离散傅里叶变换输入到频域中,并根据频谱关系画出该系统的波特图。
利用离散傅里叶变换后的输入输出数据通过MATLAB 中的系统辨识工具箱辨识得到的从SPWM调制器输入端的调制电压到逆变器输出电压的传递函数为

从图4 中可以看出,辨识所得的传递函数可以较好地拟合电压源逆变器组成的逆变电路的频率特性曲线。

图4 模型辨识曲线
2 逆变器电压鲁棒控制器的设计
当储能系统长期运行时,其系统参数如滤波器参数会发生变化,使得供电质量下降。鲁棒控制器是基于能反应系统的真实物理特性的传递函数族P 来进行设计的。它不仅能粗略表示系统物理特性的标称模型G,即上一章节中通过辨识得到的传递函数;还会考虑系统的不确定性即系统受外界干扰以及参数变化等因素引起的扰动,二者组成一个广义被控对象,如图5 所示。其中,Δm为规范化不确定性加性摄动,并且‖Δm‖≤1;Wm为加性不确定性加权函数;r和y分别为输入输出。

图5 广义被控对象
鲁棒控制器的设计可以使广义被控对象达到稳定,并且具有较好的跟踪性能[18]。其控制思想的核心是最小化干扰对输出的影响。
2.1 模型的不确定性
由式(9)中的传递函数以及图5 的模型辨识曲线可以看出,系统的真实物理特性在标称模型上下波动,这是由于受参数摄动、传感器灵敏度以及电力系统的扰动误差等影响,通过正弦扫频信号激励储能逆变器辨识得到的标称模型不能完全描述系统真实的物理特性。因此,将储能逆变电路的外界干扰和建模误差看作模型的不确定性,则储能逆变器的真实模型可以描述为

通过实验确定逆变器工作系统的标称模型G(s)与实际系统在频率不同时的最大相对误差,系统工作原理如图6所示。在1~100 Hz的频率范围内选择多个频率的激励信号rx,对逆变电路进行激励,得到稳态误差的最大值ex。通过多次实验,测得标称系统在期望频率范围内的加性不确定性上界如图7所示。

图6 系统工作原理
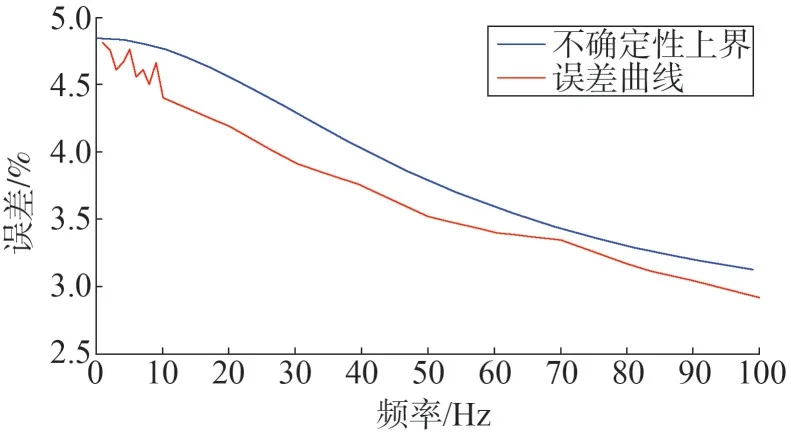
图7 加性不确定性
通过对最大误差进行估计,可以得到G(s)的一个一阶不确定性上界Wm(s)如下所示。

经过上述工作求得系统的不确定性之后,按图8所示进行线性分式变换(Linear Fraction Transformation,LFT),其中输入为Z=[r u w]T,输出W=[y zwe]T,可以求得广义被控对象P为
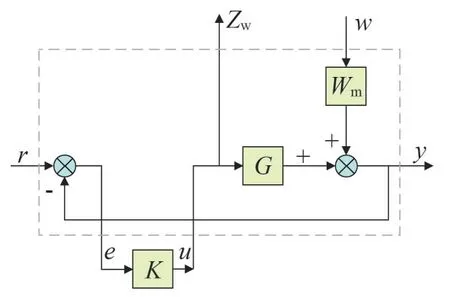
图8 LFT变换
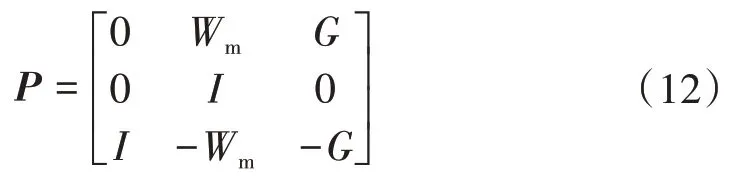
控制系统如图9所示,其中w是模型不确定性的输入,r为期望值即参考输入。

图9 控制系统
经过上述LFT 变换,储能逆变器输出电压的控制问题就转化为标准的H∞鲁棒控制问题[19]。
2.2 H∞鲁棒控制器设计
H∞鲁棒控制器的作用是当系统不确定性Δm(s)和外部干扰噪声存在的时候,保证系统仍然能够稳定地运行,使系统的输出能够跟踪期望输入,并且能够增强整个系统的抗干扰的性能,从而使储能系统可以对电网进行高可靠供电。H∞鲁棒控制系统的系统如图9 所示。其中,r为期望值即参考输入电压udqref,y为输出即母线电压udq,G为建模得到的供电台区储能逆变器的标称模型,Wm(s)为上面小节中通过实验确定的模型加性不确定性上界,Δm(s)是规范化加性不确定性,K为待设计的鲁棒控制器,u为控制器的输出,e为期望值与实际值的误差。
这样,逆变器的输出电压的控制问题就可以变换为标准的H∞控制问题。标准的H∞控制框图如图10 所示,其中输入为r=[udqref,Z]T;输出为y=[udq,W]T,P为广义被控对象,如图9 所示的虚线框内所示;K为待设计的鲁棒控制器。
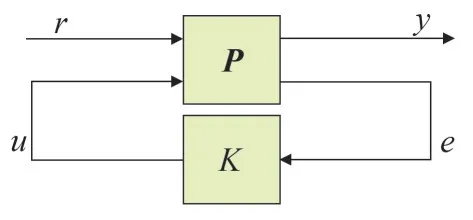
图10 标准的H∞控制
于是有
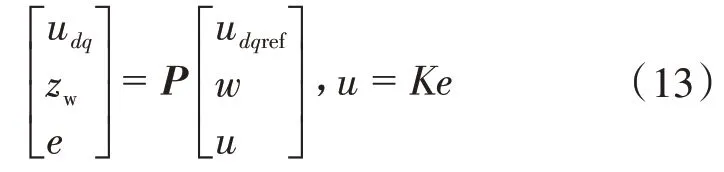
式中:zw为控制器的不确定性。因此,为保证供电台区系统的鲁棒稳定性,并抑制Z对输出的影响,要解决的抗干扰问题转化为设计一个输出反馈控制器K,使台区中的逆变器输出电压闭环系统稳定,并且使Pzω的H∞范数最小,即

根据标准的H∞鲁棒控制器解法,并利用MATLAB 中的Hinfsyn 函数进行控制器的求解,得到四阶鲁棒控制器为
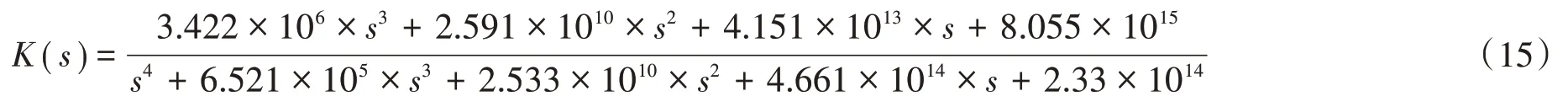
对加控制器的闭环系统进行频域分析,得到闭环系统的波特图[20],并与开环系统的波特图做比较,如图11 所示。图11 中G为开环传递函数,GC为闭环传递函数。
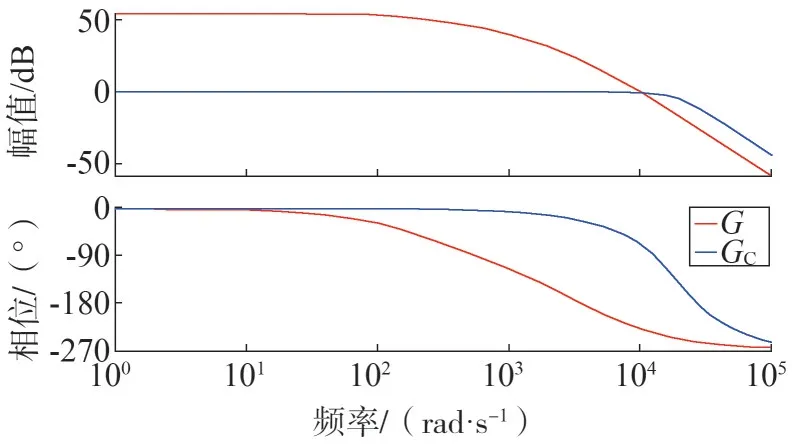
图11 系统开环与闭环波特图对比
3 仿真验证
为验证所提出的基于鲁棒控制的储能逆变器控制策略的可行性和正确性,在MATLAB/Simulink 仿真平台中,根据图1 中系统的基本结构框图搭建了电压源型逆变器下垂系统模型,仿真参数如表1 所示。储能逆变器始终工作在孤岛状态,带三相阻性负载,通过仿真验证系统在突加或突减负载的情况下,系统的输出电压输出频率及输出功率的变化,验证储能系统对电网调峰的需求,同时观察系统参数变化时,电压电流谐波含量相较于传统控制策略的提升,满足其调峰调压调频一体化要求。

表1 系统仿真参数
本文的控制算法主要对系统输出的三相电压和频率进行控制,为了简化模型以突出对逆变器控制问题的突出讨论。
3.1 负载投切工况对比
设置仿真时间为1.2 s,最初系统处于单机孤岛运行状态,带一个有功功率为5 kW(380 V/50 Hz),无功功率为2 kvar(380 V/50 Hz)的三相对称阻性负载,在0.4 s 时,系统突加一个有功功率2 kW,无功功率为2 kvar 的阻性负载,在0.8 s 时突减该负载。利用不同负载的投切模拟负载突变的情况。观察系统的动态响应的暂态过程。整个过程,系统输出的电压波形和电流波形如图12和图13所示。
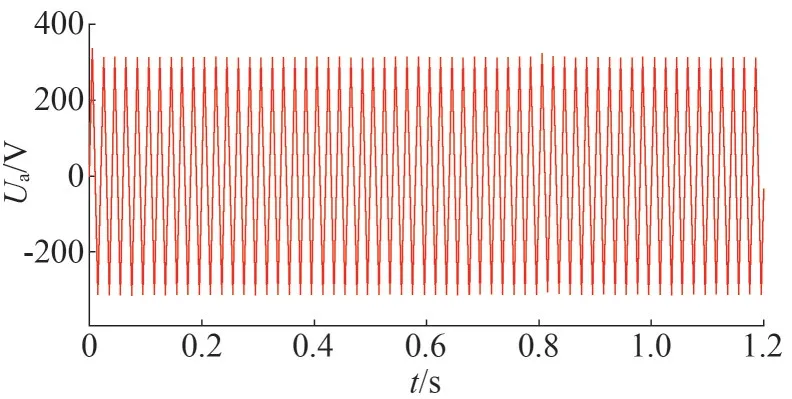
图12 逆变器输出电压波形
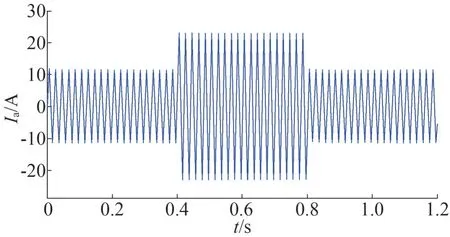
图13 逆变器输出电流波形
由图12 可以看出,当负荷变化时,输出电压开始时经过小幅震荡的暂态过程后,进入稳态输出波形无明显大幅变化。由此可以验证所选的加权不确定性函数对应的鲁棒控制器具有较好的电压波动抑制能力。图13 中可以看出输出电流的大小随着负载的变化而变化,暂态响应时间短,且在负载变化时可以快速达到相应状态。从而可以看出此控制方法具有良好的跟踪特性。
采取传统VSG 控制策略与采用的鲁棒控制策略后系统输出的有功功率对比,如图14所示。两种控制策略下系统输出电压的频率变化如图15所示。

图14 不同控制策略的输出有功功率
由图14 可以看出,传统控制策略在刚开始接入负荷时,震荡较明显,超调量过大,且当负荷突变时,输出的有功功率也瞬时突变。而采用鲁棒控制器的输出为较平滑的曲线,且在负荷变化时几乎无超调。由图15 可以明显看出,采用传统控制策略的频率变化幅度更大,鲁棒控制器可以恢复由负荷变动引起的频率变化。
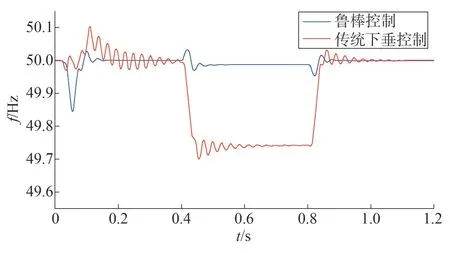
图15 不同控制策略的频率
3.2 参数变化工况对比
在仿真模型中,滤波器的电感和电阻中加入白噪声,模拟参数在一定范围内的无规律变化,分析系统输出的跟踪和适应能力,结果如图16—图19所示。
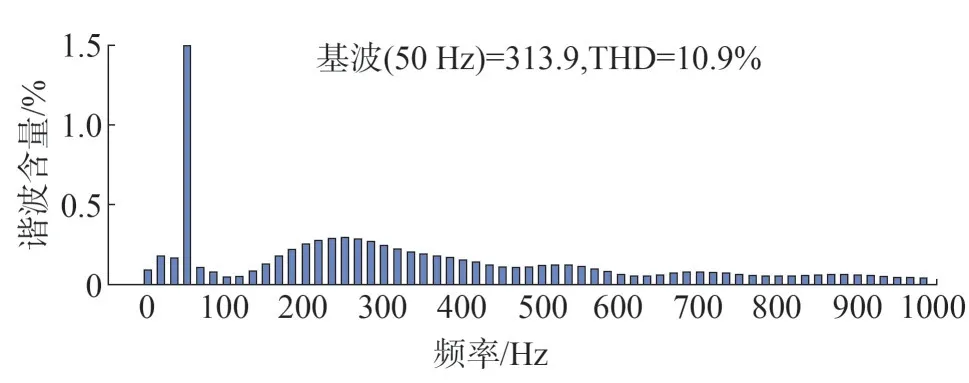
图16 参数固定时传统控制电压谐波分析

图17 参数固定时鲁棒控制电压谐波分析

图18 参数变化时传统控制电压谐波分析

图19 参数变化时传统控制电压谐波分析
由图16 和图17 中两种控制方式电压谐波分析可知,鲁棒控制策略的三相电压谐波含量(Total Harmonic Distortion,THD)为0.26%,传统下垂控制策略的电压谐波含量1.09%,传统下垂控制虽在标准范围内,但电能质量较鲁棒控制相比明显下滑。但当参数出现变化时,如图18 和图19 所示,传统下垂控制的电压谐波含量突增至3.43%,电能质量明显下滑,采用本文所述的鲁棒控制策略的电压谐波含量仅增加了0.47%,电能质量得到明显改善,由此可见其可以良好跟踪系统输入的特性。
4 结语
在电力系统中,一个供电台区具有多元用户对象,虚拟同步发电技术中的下垂策略作为储能逆变器常用的控制策略,其控制策略的好坏决定了分布式电源接入供电台区的稳定性。传统VSG 控制是在理想状态下线路阻抗呈感性时得到的理想模型,实际控制中必然存在线路损耗与外界干扰。本文在下垂控制策略的基础上,根据系统运行的输入电压与输出电压的实验数据辨识得到系统的数学模型,加入H∞鲁棒控制器以改进由传统VSG 控制引起的电压跌落,同时使系统频率偏移量减小,根据系统干扰和误差建立的不确定性加权函数,可以有效跟踪系统输入,提高系统抗干扰能力,从而满足储能系统有效参与电网削峰填谷、调频调压等功能中。
