电子式电压互感器的建模与传变特性仿真分析
2022-11-06李其莹刘祥国于文斌
李其莹,尹 东,刘祥国,万 斌,于文斌
(1.国网山东省电力公司泰安供电公司,山东 泰安 271000;2.国网山东省电力公司,山东 济南 250001;3.哈尔滨工业大学,黑龙江 哈尔滨 150001)
0 引言
随着智能电网的发展和新型电力系统的构建,未来电网的电压电流信号将呈现宽频化特征,除了工频稳态信号外,还包括大量中低频、中高频暂态信号和高频暂态信号[1-3]。电压电流互感器作为智能变电站实时测量的重要设备,其传变特性对构建智能电网全景信息系统非常关键[2]。
常规电压互感器,特别是在高电压等级电网中被广泛应用的电容式电压互感器(Capacitor Voltage Transformer,CVT),受限于测量频带问题,主要用于工频电压测量,对于谐波和暂态电压测量无能为力[3-7]。文献[4-5]讨论了常规电压互感器暂态传变能力对基于暂态行波信号的行波测距精度和行波保护性能的影响;文献[6]仿真分析了不同因素对CVT暂态特性的影响;文献[7]提出了通过增加电容来扩展CVT 测量频带的方法。常规电压互感器由于测量频带有限已经不能满足新型电力系统对电压感知的宽频化需求。
电子式互感器的应用是智能变电站的主要特征之一[8-9]。目前已有多种原理和结构的电子式互感器被广泛应用在智能变电站建设中[10-14],但大多数只利用了工频和谐波信号传变能力[15-18]。文献[15-17]讨论了EVT 在谐波计量中的应用;文献[18]提出了利用电子式互感器二次谐波分量判据,切换高、低值比率制动曲线的自适应差动保护方法。电子式互感器的优势除体现在谐波测量方面,在暂态传变能力方面更为突出[19-24]。文献[19]仿真分析了电容分压型电子式电压互感器(Capacitive-divider Type Electronic Voltage Transformer,CEVT)的暂态响应和重合闸问题;文献[20]分析了ECVT 对多种暂、稳态扰动信号的测量性能;文献[21]分析了CEVT对暂态高频信号的频率响应特性和传变优势;文献[22]探究了在一次侧不同相角下短路和带滞留电荷重合闸暂态过程中光学电压互感器(Optical Voltage Transformer,OVT)的暂态响应特性;文献[23-24]分析了EVT 的行波传变特性。上述文献主要是针对单一类型的EVT 进行分析,但目前实用化的EVT 有多种类型,其传变特性也存在一定的差异。因此,有必要对典型EVT 的传变特性进行深入研究和比较分析,特别是对高频暂态信号的响应特性。
针对上述问题和现状,本文以电阻分压型电子式电压互感器(Resistance-divider Type Electronic Voltage Transformer,REVT)、CEVT 和OVT 等几种典型EVT 作为研究对象,通过等值电路模型构建传递函数,获得其频率响应特性。依据传递函数,建立典型EVT 的PSCAD 仿真模型,分析其暂态响应特性,包括冲击响应和阶跃响应,并与广泛应用的CVT 进行比较,分析其对不同暂态电压信号的传变性能,以指导电子式互感器的应用选型。
1 电子式电压互感器的原理和建模
1.1 REVT的建模
在中低压输电线路中,REVT得到了较多的工程应用,其等效电路如图1 所示[24-27]。若不考虑杂散电容,其基本原理比较简单,就是高压臂分压电阻R1与低压臂分压电阻R2构成的分压电路。

图1 REVT等效电路
高低压臂电阻一般采用无感设计,以减小杂散电容。在电压等级比较低时,高低压臂电阻阻值一般只需要达到千欧级,而杂散电容一般为皮法级,此时杂散电容的影响较小。但当REVT 应用于高电压等级时,为保证电阻消耗功率不超过限值,高压臂电阻阻值能够达到兆欧级,此时杂散电容对高频暂态信号的影响就不可忽略。
由等效电路,可以获得REVT输出电压u2与输入电压u1的关系式为

式中:Ch为高压臂电阻对高压侧杂散电容;Cg为低压臂电阻对地杂散电容。
对式(1)进行拉氏变换,获得REVT 电阻分压部分的传递函数为

从式(2)可以看出,考虑到电阻和电容的大小,在频率达到几千赫兹时,须考虑杂散电容对传变性能的影响。
1.2 CEVT的建模
目前在智能变电站中应用最为广泛的电子式电压互感器为CEVT,其等效电路如图2 所示[20,24,28-31],由电容分压器和取样电阻R组成,C1、C2分别为电容分压器的高压臂电容和低压臂电容。其电容分压器与常规电容分压器结构类似,不同的是额定容量在毫瓦级,输出电压一般不超过5 V。

图2 CEVT等效电路
根据等效电路,可以获得CEVT输出电压u2与输入电压u1之间的关系为
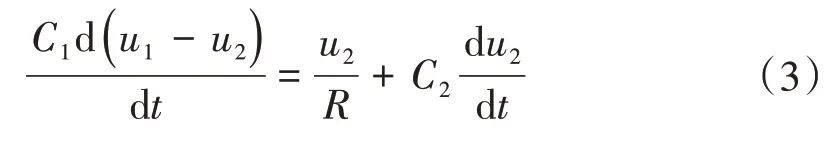
对式(3)进行拉氏变换,可获得CEVT 电容分压部分的传递函数为

当ωR(C1+C2)≪1时,有:

由式(5)可知,在一定的频率范围内,CEVT 的输出电压与输入电压的微分呈正比。此时,须通过积分电路对采样电阻的输出进行积分,才能获得与输入电压呈线性变化的二次电压。
在实际应用中,积分器的选择也很重要。图3 为常用的有源积分器电路,采用直流负反馈稳定积分器的工作点,在积分电容C1两端并联反馈电阻Rf,使得积分器能够长期稳定工作。此时,积分器的传递函数为

图3 有源积分器电路
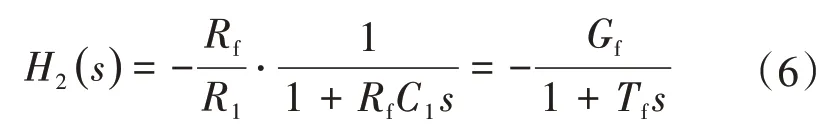
式中:Gf为增益;Tf为积分时间常数,可表示为:
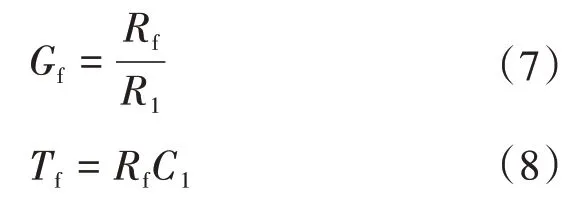
1.3 OVT的建模
目前实用化的OVT 是基于Pockels 电光效应的光学电压传感器,目前已经被应用于宽频电压的测量[3],其结构和原理如图4所示。
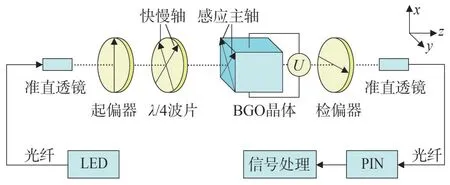
图4 OVT的结构和测量原理
图4 中,OVT 以锗酸铋(Bi4Ge3O12,BGO)晶体为传感材料,主要包括LED 光源、起偏器、检偏器、λ/4波片、电光晶体、准直透镜和PIN光电探测器[32-36]。
OVT 的基本测量原理为:LED 光源发出的光通过起偏器后产生线偏振光,在外加电压U的作用下,波长为λ的线偏振光通过长度为l的电光晶体时,出射的两束光产生的相位差可以表示为
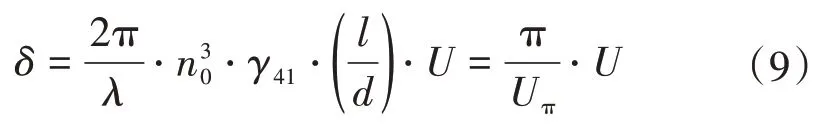
式中:n0、γ41分别为BGO 晶体的折射率和线性电光系数;d为外加电压方向的晶体厚度;Uπ为晶体的半波电压,且Uπ=。
由式(9)可知,要获得外加电压U,须准确测出相位差δ。采用双光路处理方案,OVT 两个光路输出信号为

式中:P为传感光路的静态工作光强,μW;A为光电转换系数,V/μW;Gq为前置放大倍数。
采用差除和方案,可得到OVT的输出为

式中:ui为输入电压;K电光效应常数,表示为
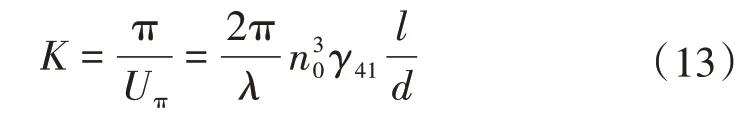
由此,OVT光学电压传感器的传递函数为

由式(14)可知,OVT 的输出电压正比于输入电压。原理上,OVT 没有频带和响应时间问题,这是OVT的最大优势。
一般BGO 晶体的Uπ只有几十千伏,所以在电压等级比较高的应用场合,一般先利用电容分压器从被测高压线路上分出一个较低的几千伏电压,再利用并联在电容分压器低压电容两端的光学电压传感器进行测量,设计成电容分压型光学电压互感器(Capacitive-divider Type Optical Voltage Transformer,COVT),其基本结构如图5所示[35-36]。

图5 COVT的基本结构
COVT 对传变特性起决定作用的是电容分压器和光学电压传感器。
对于理想电容分压器,其低压电容C2两端电压可以表示为
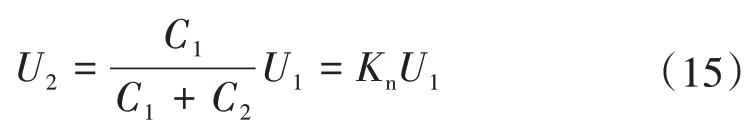
式中:U1为输入电压;Kn为电容分压器分压比,表示为

由式(16)可知,只要适当选择高压电容C1和低压电容C2的电容量,即可得到光学电压传感器所需分压比。
考虑杂散电容时,低压电容C2两端电压为[34]
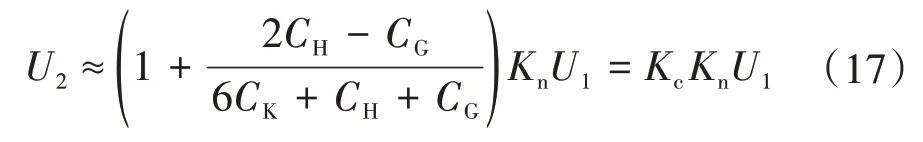
式中:Kc为杂散电容引起的分压比误差系数,可表示为
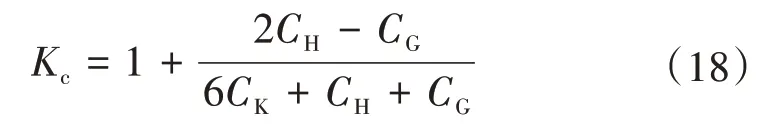
式中:CK为电容分压器总电容量;CH和CG分别为高压臂和低压臂的杂散电容。
由式(18)可以看出,杂散电容仅引起电容分压器的幅值误差。结合式(12)描述的光学电压传感器的输出方程,COVT的传递函数可表示为

COVT 的传递函数与式(14)所描述的OVT 的传递函数之间仅差比例系数,所以COVT 和OVT 传变性能基本是一致的。
1.4 低通滤波器的建模
电压信号在传输过程中不可避免地会受到高频噪声干扰信号的影响。因此,一般会在信号处理的模数转换前加入低通滤波环节。
巴特沃斯低通滤波器是最常用的低通滤波器,巴特沃斯低通滤波器又称为最大平坦幅频响应滤波器,一般选用两阶巴特沃斯低通滤波器。巴特沃斯低通滤波器是一种全极点配置的滤波器,对于两阶巴特沃斯滤波电路,如果截止频率为ωc,那么对应的典型全极点巴特沃斯低通滤波器的传递函数可表示为
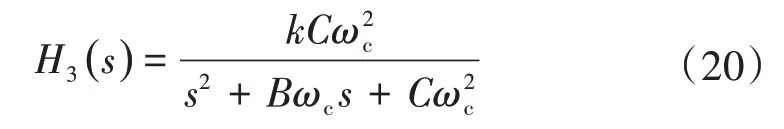
式中:B、C为巴特沃斯归一化系数,可以通过查归一化系数表获得,本文取B=和C=1;k为滤波器增益。
如图6 所示为基于巴特沃斯滤波器原理设计的有源低通滤波器电路。根据需要确定截止频率后,通过计算可得到滤波电路电阻、电容的设计值。
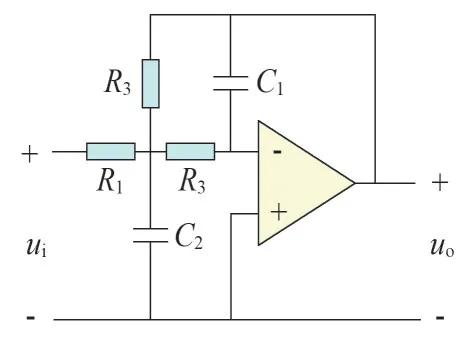
图6 有源低通滤波电路
本文主要研究EVT 的暂态响应特性,模型中所有涉及低通滤波器的截止频率均设置为1 MHz。
2 电子式电压互感器的频率响应特性
依据建立的传递函数,仿真分析上述典型EVT的频率响应特性。
2.1 REVT的频率响应
REVT的典型结构主要由电阻分压器、放大电路和低通滤波电路组成,表1为某REVT 电阻分压器的电气参数,图7为其频率响应。

表1 REVT电阻分压器电气参数

图7 REVT的频率响应特性曲线
从图7 所示REVT 的频率响应特性曲线可以看出,在此设计参数下,此REVT 在10 kHz 以内能基本保证准确传变,由于杂散电容的影响,随着信号频率的提高,其幅频响应在高频段将会出现幅值较大的冲击。
2.2 CEVT的频率响应
CEVT 的典型结构主要由电容分压器、放大电路、积分器电路和低通滤波电路组成,表2 为CEVT电容分压器电气参数,图8为其频率响应。

表2 CEVT电容分压器电气参数

图8 CEVT频率响应特性曲线
从图8 所示CEVT 频率响应特性曲线可以看出,CEVT 不能传变直流分量,在此设计参数下,其基本带宽在1 MHz 左右,频率响应特性比较好。改变分压器电容和取样电阻的参数会影响带宽和响应时间。
2.3 OVT的频率响应
OVT 的典型结构主要由光学电压传感器、放大电路和低通滤波电路组成,表3 为OVT 电光晶体参数,图9为其频率响应。

表3 OVT电光晶体参数

图9 OVT频率响应特性曲线
从图9 所示OVT 频率响应特性曲线可以看出,由于光学电压传感器传递函数为常数,所以OVT 的带宽主要决定于低通滤波器的截止频率,本文设置为1MHz。根据上文分析,COVT 的频率响应特性与OVT 是基本一致的,在此不再累述。表4 为COVT 的电容分压器参数。

表4 COVT电容分压器参数
3 电子式电压互感器的暂态响应特性
依据传递函数,在PSCAD 仿真平台建立上述典型EVT 的仿真模型,形成PSCAD 的EVT 模型库,比较分析EVT 与常规CVT 的暂态响应特性,其中CVT利用PSCAD元件库中的模型进行仿真。
3.1 全偏移暂态响应
为考察不同类型电压互感器(Voltage Transformer,VT)对直流和非周期分量的响应特性,用下式描述的暂态电压作为电压互感器仿真模型的输入为

式中:Upsc为一次电压对称分量方均根值;φp为初始相位;τp为一次时间常数。
当一次时间常数设置为τp=100 ms时,图10为不同类型VT的全偏移暂态响应对比图。

图10 不同类型VT全偏移暂态响应对比
仿真结果表明:所有EVT 的二次输出电压信号均与一次输入工频电压信号曲线基本重合,误差很小。而CVT由于其不能准确传变直流和非周期量,所以在进入稳态前不能准确跟踪一次电压信号,出现很大的传变误差。
3.2 单相接地故障仿真测试
图11 为A 相接地短路故障仿真系统图,故障时刻0.2 s,故障持续时间为0.02 s。取故障点电压信号作为仿真模型输入,观测电压互感器模型对单相接地故障的暂态响应,图12 为不同VT 的暂态电压响应对比。

图11 A相接地短路故障仿真系统

图12 不同类型VT的接地故障暂态响应对比
仿真结果可以看出:在此系统短路故障情况下,CEVT 和OVT 能很好地跟踪故障电压波形;而REVT由于杂散电容的影响,在电压突变点存在持续时间很短的大冲击振荡过程;而CVT也由于电容分压器和电磁单元电感的原因在电压突变点存在过渡过程。
3.3 带滞留电荷重合闸暂态过程的仿真测试
图13 为带滞留电荷重合闸暂态过程PSCAD 模拟电路,选择国标GB 20840.7 中所提及的最严重的情况进行仿真,在一次电压达到正峰值时瞬时打开开关BRK,再在一次电压达到正峰值时瞬时闭合开关BRK1。图14 为不同类型电压互感器对带滞留电荷重合闸暂态过程仿真对比图。

图13 带滞留电荷重合闸暂态过程模拟电路


图14 不同类型VT对带滞留电荷重合闸暂态响应对比
仿真结果可知:当出现带滞留电荷重合闸的情况时,OVT 的二次输出能够实时准确跟踪一次电压的变化,其传变特性不受影响;CVT 由于不能传变直流分量,很快衰减到零值,合闸之后还有个振荡稳定过程,CVT 不能真实地反映一次电压的突变,且存在一定的响应时延;CEVT 的暂态过程最严重,重合闸瞬间其二次输出电压出现了较大的暂态电压;REVT由于杂散电容的影响,在重合闸瞬间也产生了较大的暂态电压。
3.4 冲击响应
按照IEEE、IEC 标准通常用于雷电分析的波形要求,仿真时的冲击信号源用双指数函数实现,可以描述为
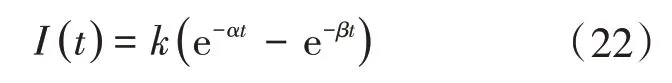
式中:k、α、β为常数,具体参数可以根据标准要求设置。
图15 为不同类型电压互感器模型的冲击响应对比图。仿真结果可以看出:CEVT 和OVT 的冲击响应特性优异,能很好地跟踪冲击电压信息;REVT 对冲击电压的跟踪响应比较好,但存在初始电压出现很大的冲击振荡过程,由理论分析可知,这主要也是由杂散电容的存在引起的。而CVT的测量频带受限,不能准确传变高频信号,因而不能传变冲击电压信号。

图15 不同类型VT的冲击响应对比
3.5 阶跃响应
对于交流测量,一般关注互感器的额定延时;而对于直流测量,更关注互感器的阶跃响应时间。GB/T 26216.1—2019《高压直流输电系统直流电流测量装置第1 部分:电子式直流电流测量装置》规定:最大过冲小于20%;上升时间(达到阶跃值90%的时间)小于400 μs,柔直系统要求小于25 μs;趋稳时间(幅值误差不超过阶跃值1.5%)小于5 ms。
图16 为不同类型VT 的阶跃响应对比图。仿真结果可见:在此参数设置下,所有类型的VT 的阶跃响应时间均小于100 μs,都能满足标准对阶跃响应时间的基本要求。但是,CEVT 由于电容分压器和取样电阻构成放电回路,随着RC 时间常数逐步放电,阶跃响应逐步衰减到零值,不能直接用来测量直流信号。而CVT的测量频带受限,不能测量直流和非周期分量,阶跃响应很快就衰减到零值,所以CVT也是不能用来测量直流信号的。

图16 不同类型VT的阶跃响应对比
4 结语
传统电压互感器由于测量频带有限、暂态特性较差,已不能满足新型电力系统对电压感知的宽频化需求。面向未来新型电力系统和数字电网的建设,电压测量将从常规电压互感器向EVT 转型,EVT 将会引来新的发展机遇。
本文构建了REVT、CEVT 和OVT 等典型EVT 的传递函数,获得了它们的频率响应特性。依据传递函数,建立了典型EVT 的PSCAD 仿真模型,分析了其暂态响应特性,包括冲击响应和阶跃响应,并与广泛应用的常规CVT 进行比较。仿真结果表明:与常规CVT 相比,三种典型EVT 有着较好的频率响应和暂态响应特性。其中,CEVT 在带滞留电荷重合闸操作中会产生较严重的暂态过程,重合闸瞬间其二次输出电压有可能出现较大的暂态电压,由于不能传变直流分量,所以CEVT 一般只用于交流电压的测量。REVT则由于在高电压应用中需选择兆欧级大电阻,其杂散电容的影响明显,使得其测量带宽受限,且对高频暂态电压冲击会出现较大的暂态振荡过程,因此REVT 一般只在中低压等级电网使用。而OVT 原理上测量频带不受限制,能在全频带准确传变一次电压信号,其测量频带主要受信号处理和AD采样的限制,其冲击响应和阶跃响应特性表现优异,是宽频电压感知的理想传感器,OVT 将会成为构建新型电力系统宽频化电压感知的重要技术手段。
本文仅给出了典型设计参数下EVT传变特性的仿真和分析,EVT 的传变特性会随着设计参数的改变而发生变化,温度等运行环境的不同,也会对EVT的传变特性带来一定影响。下一步应将设计参数改变、环境温度变化等考虑进来,对建立的EVT 的PSCAD 仿真模型进行不断完善,为新型电力系统数值仿真提供实用的电压测量仿真模型库。
