振荡潜流带沉积层-水界面污染物输运的研究1)

陈金峰 张金龙 杨文武 董宇红

(上海大学力学与工程科学学院,上海市应用数学和力学研究所,上海 200072)

引言

在工业化和城市化快速发展过程中,污染废水和生活用水在排放到江河湖海之前会经过无害化处理[1].当外部污染源得到有效控制后,沉积层成为更突出的潜在污染源.相关研究表明,我国水体潜流带沉积物的污染率高达80.1%[2].当水流遇到扰动或水体的环境条件(如酸碱度、溶解氧含量等)发生改变时,沉积层中的各种污染物如重金属离子会再次释放到上覆水体中,造成二次污染[3-4].沉积层-水交界面(sediment-water interface,SWI)是沉积层与上覆水体间进行物理、化学、生态作用的主要区域之一.上覆水的流动特性和沉积层的物质和结构属性很大程度上影响跨越SWI 的物质输运过程[5].研究河口海岸流动和沉积层中污染物的输运机理和传质规律,以及研究潜流带流场统计特性、相干结构和猝发事件与物质输运的关系是科学界、工程界共同关注的课题,对于认识和保护水资源生态具有重要的科学意义.

在河口、湖泊、海岸带等地区,潮汐、内波、风荷载、水泵作业等多种因素会产生振荡流动现象[6].不同因素所产生的振荡流中,其振幅和频率差异性很大,导致物质输送中的动力学过程更为复杂.因此,有必要研究振荡流条件下的潜流交换对沉积层内外污染物释放与输运的影响.

以往研究表明,在低速平缓流动和沉积物不发生悬浮的情况下,SWI 处通常存在厚度以毫米计的扩散边界层,分子扩散是控制这一区域物质垂向输运的主要机制[7].但是当上覆流动复杂化,如湍流状态或振荡流时,对SWI 区域的混合和输运过程需要加以深入研究[8-9].Spalart 等[10]数值研究了受扰动的层流和间歇湍流模式,并分析了壁面应力和流速分布.Reidenbach 等[11]采用大涡模拟方法研究了高Reynolds 数下的振荡湍流边界层及转捩问题,进一步拓展了此类问题的研究.

随后,一些学者将研究聚焦到流体混合和传质方面,涉及到的溶质包括溶解氧、营养盐等.Lorke等[12]在瑞士的阿尔卑纳赫湖测量了周期为18 小时的振荡流中溶解氧垂向分布情况.数据显示大幅振荡的流动导致了SWI 区域质量通量的不稳定性.Higashino 等[13]通过数值模拟发现溶解氧浓度和Sherwood 数的波动幅度与振荡周期、振幅和Schmidt 数有关.Tian 等[14]研究了非恒定的驱动条件下高Schmidt 数传质过程.研究发现,低频高振幅的振荡压力梯度驱动力对流动和物质输运有显著影响.Wang 等[15]进一步研究了振荡流下的氧浓度垂向分布、SWI 区域的湍流通量和沉积层耗氧量随时间的变化规律.Thomas 等[16]研究发现表面波诱导的振荡流动增强了底栖生物对养分的吸收速率.虽然通过实验和实地测量总结了一些质量输运经验公式可以预测水体沉积层溶质的吸收释放率[17].

以上研究主要关注潜流交换中“自上而下”的物质输送过程,而累积于沉积层内的污染物质则是在受到扰动后“自下而上”的释放和扩散过程.Cheng 等[18]通过水槽实验测量了沉积层内的磷向水体中释放过程中的浓度变化,分析了平均流速、周期和振幅等水动力因素对其的影响.注意到以往对潜流带中污染溶质输送的研究多着眼于其分布特点和污染水平[19],较少涉及复杂水动力条件和底床物理特性(如渗透性、孔隙率等).基于以上分析,本文运用大涡模拟方法对具有沉积层的振荡槽道流和其中高Schmidt 数污染物传质问题展开研究.通过求解三维不可压缩黏性Navier-Stokes (N-S)方程和对流扩散方程来模拟沉积层内外的流动和传质过程,同时采用修正的Darcy-Brinkman-Forcheimer 模型描述有锌离子污染溶质的可渗透沉积层.研究聚焦于振荡流和界面上下物质输运过程的耦合作用,探究不同振荡条件对动量输运和污染物溶质输运的影响,以及由此产生的沉积污染物的释放和输送规律与机制.

1 数理模型与数值方法

1.1 物理模型与控制方程

在研究含有沉积层的污染溶质输运中,湍流运动特性与跨SWI 的质量通量之间依赖关系是一个重点,这对实验测量有相当的难度,而模型化和数值模拟则具有优势.本文物理模型如图1 所示,x,y,z分别代表流向、法向和展向,物理模型的计算域为Lx×Ly×Lz=2πh×1.1h×1.5πh,对应的网格数目为Nx×Ny×Nz=128×196×128.沉积层深度为0.1h,该局部区域法向网格数为35.流向和展向为均匀网格,法向网格采用伸缩变换,适当增加壁面、自由面和SWI 处的网格分辨率,网格间距为 Δx+=25.26,Δz+=18.95,Δy+=0.43～5.61 .槽道中水层高度h取10 cm作为特征长度,SWI 处的摩擦速度uτ为特征速度,沉积层内初始浓度C0=2.34 mg/L 为特征浓度.由此,无量纲的三维控制方程为

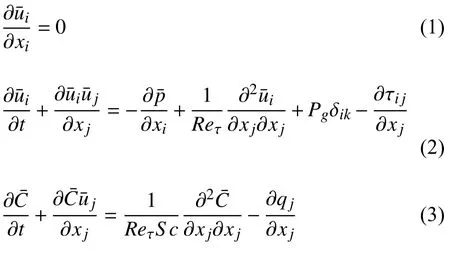
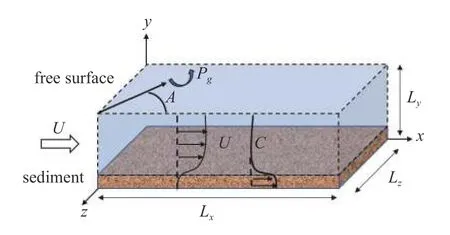
图1 底部含有沉积层上部为自由面的槽道振荡流动模型示意图Fig.1 The sketch of the oscillatory flow model of a channel with a sediment layer at the bottom and a free surface at the top

式中上划线“-”表示滤波后的变量.流向x、法向y、展向z的速度分量分别为u,v和w或ui(i=1,2,3),C为锌离子浓度.摩擦Reynolds 数定义为Reτ=uτh/υ,Schmidt 数Sc=ν/Dw,描述同时存在动量扩散及分子扩散的无量纲参数.ν是水的运动黏性系数,Dw是金属锌离子在水中的分子扩散系数.水中锌离子可被视为被动标量,其分子扩散系数相对于运动黏度小两个量级,是一种高Schmidt 数的传质现象.p表示滤波后的压力.振荡驱动力Pgδik(k=1,3)与流向形成一个夹角A,简称振荡角;T为振荡周期,该驱动力表示为

τij和qj分别为亚格子尺度湍流应力项和湍流质量通量项,这里采用的是Germano 等[20]提出的动力学亚格子模型.假定亚格子尺度湍流应力与大尺度运动应变率有如下关系,涡黏性系数进一步假设为可以得到如下数学表达式

式中S cT=νT/DT是借鉴分子输运模型定义的湍流Schmidt 数,方程式(6)和式(7)中的G和S cT将用动力学方法求出[14,21].

一般来说,沉积层具有复杂的几何结构和广泛的长度尺度特征,这些性质与多孔介质相符.Whitaker[22]提出在一个体积为V,半径为r的球型控制体上平均N-S 方程,只对多孔介质中的大尺度流动进行建模从而降低对网格的要求.这样的体积平均方程被称为VANS(volume-averaged Navier-Stokes equations)方程.对于一般的物理量 φ ,〈φ〉s表示相体平均,〈φ〉f表示固有体平均,相体平均被定义为

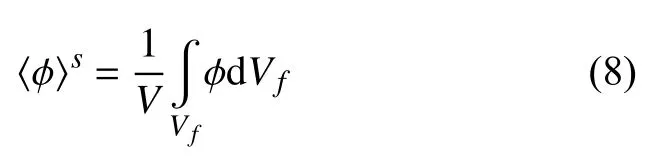
其中Vf是控制体中流体所占的体积,固有体平均被定义为

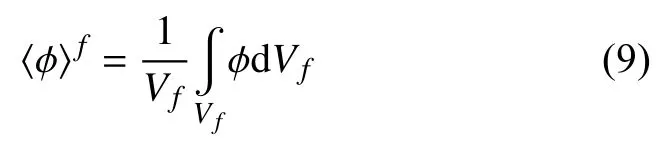
两者之间的关系为

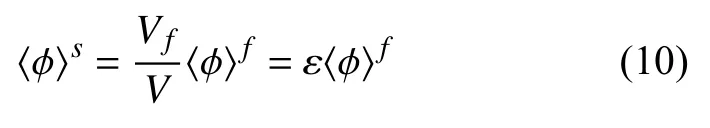
于是得到在沉积层中的流体的控制方程如下

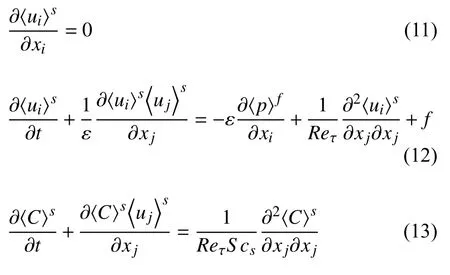
当上覆水为较高Reynolds 数流动,具有多孔渗透性的下垫沉积层间隙流速与水力梯度并非线性关系.因此本文采用修正的Darcy-Brinkman-Forcheimer 非线性模型来反映高渗透沉积层中的阻力影响[23],即

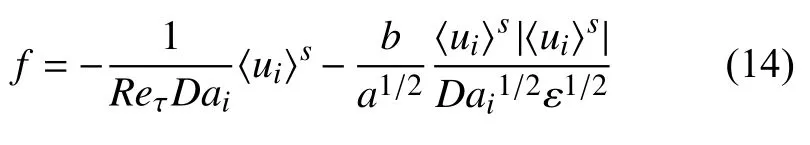
其中达西数Dai=Ki/h2表示渗透率Ki的影响,ε 为孔隙率,常数a=150和b=1.75 .

在计算中,沿槽道流向x和展向z取周期性边界条件,下壁面y=0 处取无滑移无穿透速度边界条件;在自由面y=1.1 处,不考虑变形的影响,取剪切力为零的条件,即

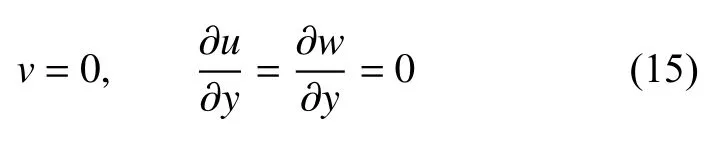
初始时刻,沉积层内污染物浓度为1,水中浓度为0;边界条件为下壁面浓度恒定为1,上方自由面处取浓度的法向通量为0.速度和浓度场在SWI 界面处采用阶跃界面条件[24-25],即

设定上述界面条件,从物理上合理给出了界面的动量传递关系,是将VANS 方程(控制多孔介质内部流动) 与N-S 方程(控制自由流动流体) 在SWI 处耦合所需的应力条件.

1.2 数值方法和验证

本文的时间离散方法为Verzicco 等[26]在Kim 等[27]分裂步方法基础上改进得到的混合格式[28].对流项的时间推进用三阶Runge-Kunta 法,黏性项采用Crank-Nicholson 隐式格式,空间导数离散采用二阶中心差分.控制方程的离散都是基于交错网格[29].

为了验证程序计算的可靠性和合理性,本文将采用大涡模拟,首先对带自由面的高Reynolds 数槽道流这一典型物理模型进行验证计算,并将结果与Moser 等[30]的直接数值模拟(direct numerical simulation,DNS)结果对比.为此,与该DNS 模拟的物理和计算参数取值一致,即Reτ=590,计算域为Lx×Ly×Lz=2πh×h×πh.本文采用的网格为128×196×128,前述DNS 网格数为 384×257×384 .图2 是平均流向速度沿法向分布,壁面坐标定义为y+=yuτ/ν .

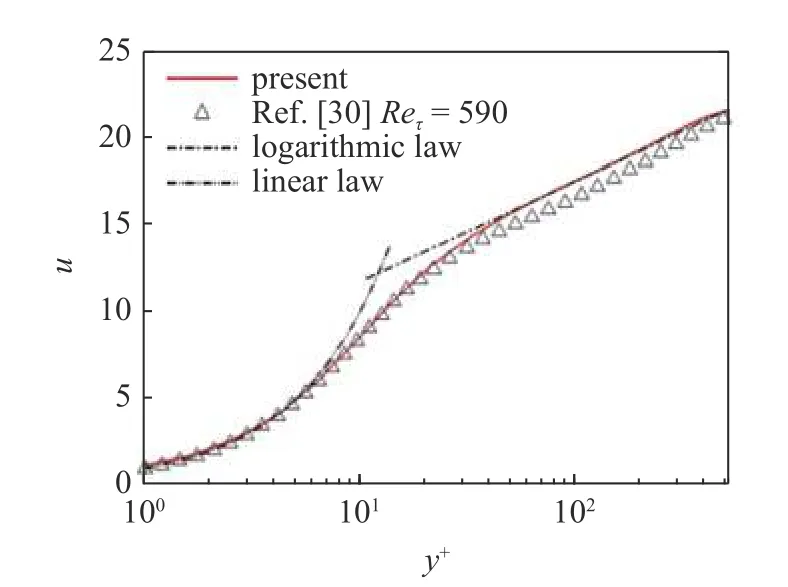
图2 流向平均速度分布Fig.2 Profiles of the mean streamwise velocity

从图中可以看出,平均速度与Moser 等[30]的DNS 结果吻合良好.在黏性底层,平均速度符合u=y+的线性律.当y+＞40,平均速度剖面符合对数律的典型分布,为u=2.5lny++5.5 .有研究表明,当沉积层中的渗透率愈来愈小时,流动特性与规范槽道流趋于一致(Ref.[31]),结果对比说明本文数值计算方法以及程序能够准确合理地预测高Reynolds数壁面剪切湍流特性.

然后,考虑到本文着重研究具有底部沉积层的高Schmidt 数传质问题,除了将上述的LES 模拟的流场统计结果与DNS 结果进行比较外,还进行了另一个数值验证,以便与O'Connor 等[32]的含有沉积层水槽流动实验数据进行比较,特别是考察对高Schmidt 数标量(溶解氧)输运和其浓度分布的模拟准确性.表1 显示了实验的相关物理参数,包括沉积层厚度h、流体黏性系数、摩擦Reynolds 数、基准浓度、Schmidt 数.这里计算与实验保持一致,取S c=373,Reτ=180 .达西数和孔隙率表示沉积层的渗透性,计算取值参照实验[32],即Da=1×10-4,ε=0.7.计算域、网格数和数值格式同上.图3 为模拟所得平均浓度在垂向的分布,同时给出了与实验数据的比较.图中SWI 表示水-沉积层交界面.将SWI 的位置平移到y=0.08,规范模拟算例与实验之间的坐标对应关系.图中可见计算的平均浓度分布与实验结果吻合良好.根据上述比较和验证,可以证实本文计算方法和程序能够准确预测带有沉积层的槽道流高Schmidt 数传质问题.

表1 流场物理参数(h=10 cm)Table 1 Physical parameters of flow field (h=10 cm)

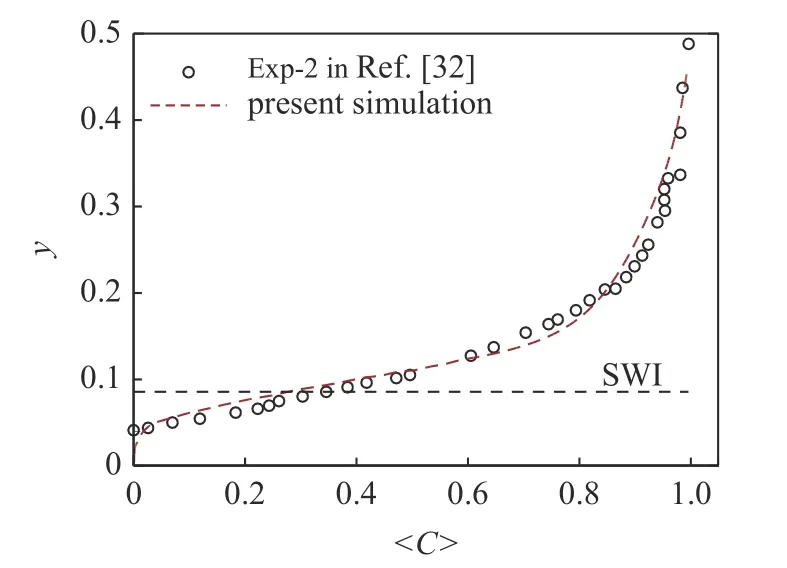
图3 平均浓度在垂向的分布Fig.3 Profiles of the mean concentration along the vertical direction

2 结果与讨论

2.1 振荡流动下浓度场与流场的相关性

在底部为高渗透沉积层的三维槽道振荡流物质输运问题中,剪切流动主导其传质过程.随机运动的流体微团和相干运动的大尺度结构为共同载体促进了高Schmidt 数标量输运行为.通过湍流各尺度之间,以及流动作用于交界面来实现其中动量、能量和物质的混合和交换.本文算例的模拟参数均设置在水温35 °C,摩擦Reynolds 数Reτ=515,Schmidt数S c=109,孔隙率ε取0.45,达西数Da为1.0 ×10-4.

表2 给出不同振荡角A和振荡周期T下的物理参数和统计量,〈〉 表示统计量在10 个周期内的时均值.水层和沉积层中的体积平均浓度分别定义为

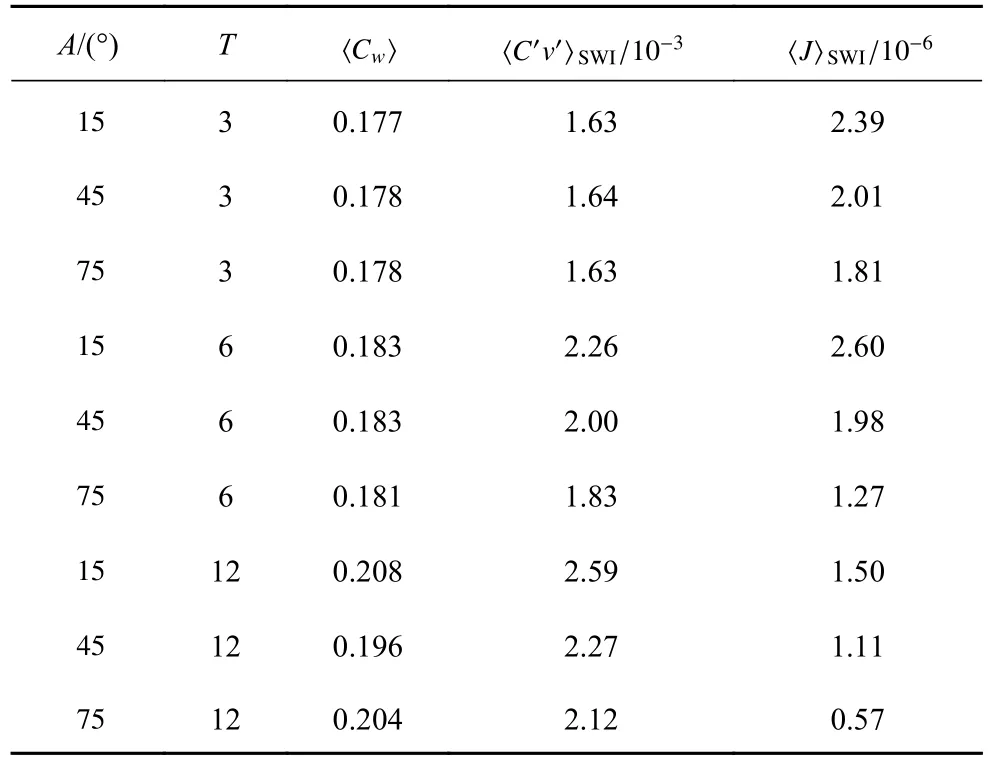
表2 不同算例的计算参数和湍流通量等统计量Table 2 Calculation parameters and statistics such as turbulent flux for different cases

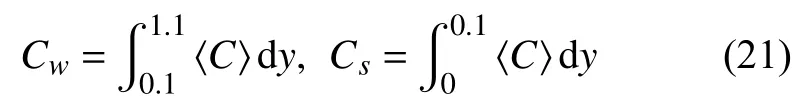
〈C′v′〉SWI和 〈J〉SWI分别为交界面处的浓度通量和分子扩散通量.

首先分析了SWI 上覆振荡流的湍流结构、速度、能量和浓度变化之间的相关性.图4 为振荡驱动力Pg与体积平均的湍动能Ek、流向速度Ub、展向速度Wb随时间的变化曲线.Ek的表达式为

体积平均的流向速度Ub、展向速度Wb均由摩擦速度uτ无量纲化得到.当流向振荡驱动力占优时,即A为15°,Ub显著大于Wb.随着振荡周期增大,Ek,Ub,Wb的波动幅度逐渐增大,如图4(a)和图4(b)所示.当振荡驱动力逐渐过渡到展向为主时,即A从45°再到75°时,湍动能Ek的幅值变化并不明显,但Ub与Wb振荡幅值相当(图4(c)),并逐渐发展出以展向速度Wb大幅振荡为特征的流动,如图4(d)所示.

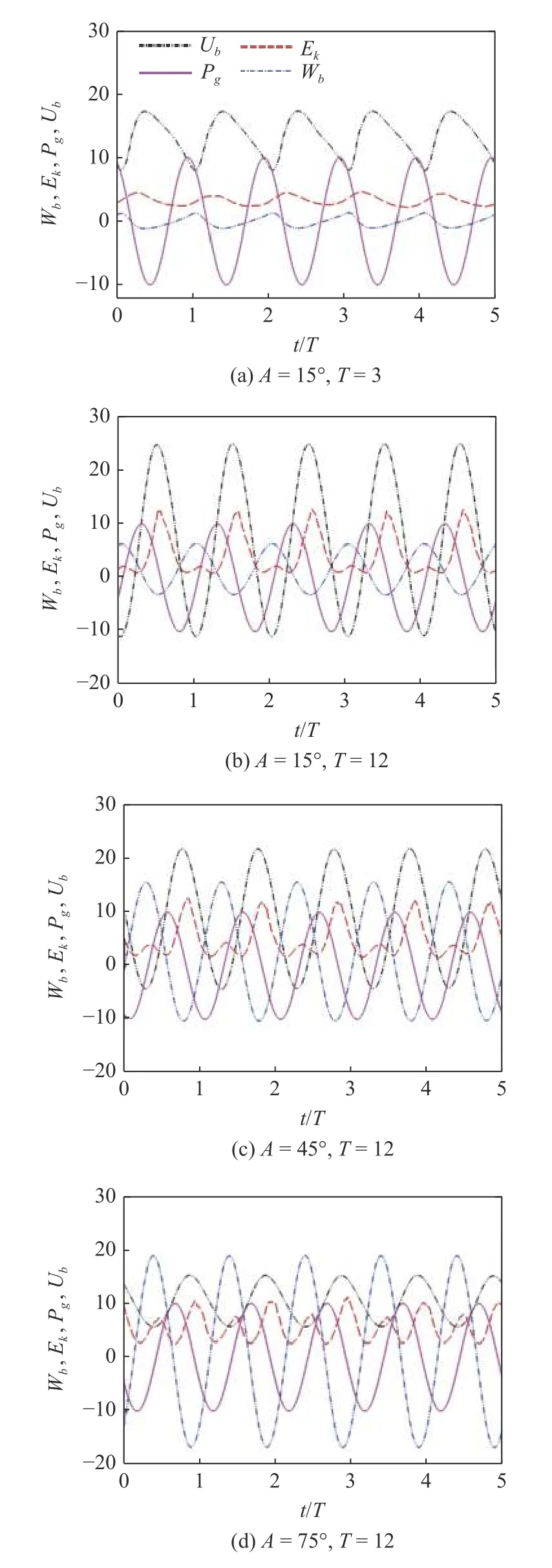
图4 振荡驱动力 Pg与体积平均的展向速度 Wb、流向速度 Ub、湍动能 Ek的关系Fig.4 Oscillation driving force versus volume-averaged spanwise velocity Wb,streamwise velocity Ub,turbulent kinetic energy Ek

图5 进一步给出沉积层内体积平均的浓度Cs、流向速度Ub和湍动能Ek随时间变化曲线.由于浓度场对流场的延迟响应,可以发现Cs与Ek和Ub之间存在明显的相位差.Ek呈现增长与衰弱的交替变化,并作用于传质过程.前者在增强过程中带动Cs持续增高,反之亦然,表明振荡中的湍流强度与高渗透沉积层中污染物的准周期扩散呈现明显关联性.当流向振荡驱动力占优时(A= 15°),高频振荡的湍流运动抑制了沉积层污染物浓度Cs的波动性(图5(a));而低频振荡使得Cs的波动幅值逐渐增大(图5(b)).当展向振荡驱动力占优时(A= 75°),虽然Ub和Ek的波动幅度明显低于A= 15°的情况,但平均浓度的波动仍较为显著(图5(a)和图5(b)),这表明低频振荡流与沉积层内污染物浓度波动的关联性更强.

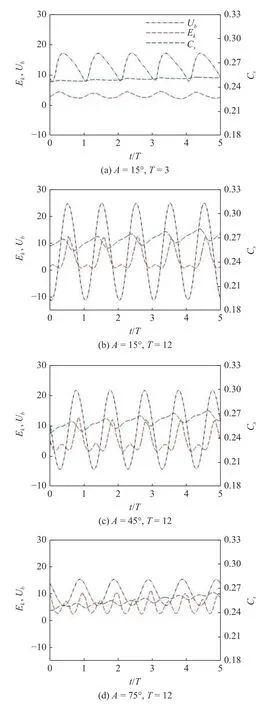
图5 体积平均的流向速度、湍动能和沉积层内浓度随时间变化曲线Fig.5 Volume-averaged streamwise velocity,turbulent kinetic energy,and concentration in sediment versus time

随时间变化的振荡驱动力不仅对平均速度场和浓度场产生重要的影响,而且在其作用下,中小尺度湍流脉动和浓度脉动的统计量也会交替地增强或减弱,呈现准周期的变化.图6 给出了不同振荡角和频率下相位平均的法向湍流强度分布.可以看到法向速度脉动增强与减弱的程度和相位均有所不同.低频振荡对于流动有显著影响,其法向脉动峰值更高,波动更强烈.

为了观察振荡驱动作用对瞬时流场结构的影响,图7 给出了A=45°,T=12 算例在SWI 上方y+=103处一个周期内不同相位的瞬时法向速度的水平等值线图.图中黑色实线和黑色虚线分别是法向湍流脉动速度v′=2.0和v′=-2.0 的等值线.在相位t/T=5/8,6/8 时,从图7(b)和图7(c)中可以看到流场中比较丰富的正负斑团结构.而如图7(a)和图7(d)所示,在相位t/T=4/8,7/8 时,因法向脉动较弱而斑团结构稀少,这与图6(c)所显示的相位平均湍流强度变化相对应.结合标注相位点的图7(e),可以观察到在第2 和3 点处,即t/T=5/8,6/8 处湍动能达到高位,此时法向速度脉动也达到峰值,如图7(b)和图7(c)所示,随后湍流强度开始减弱.法向湍流强度的这一周期性变化将会强化湍流混合,使得其质量通量在法向发生间歇性的变化,进而促进其中的物质输送和交换.

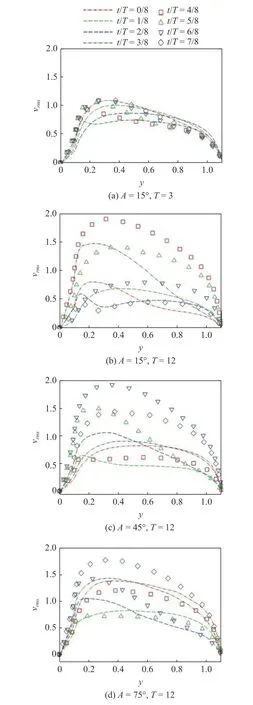
图6 相位平均的法向湍流强度Fig.6 Profiles of phase-averaged wall-normal turbulent intensities

相应地,图8 给出了A=45°,T=12 时在不同相位的法向浓度通量瞬时分布(z方向视图).法向湍流浓度通量分为两部分,蓝色部分(C′v′=0.01)为正向通量,棕色(C′v′=-0.01)为负向通量.通过图8(b)和图8(c)发现C′v′=0.01 的发生概率更大,说明正向浓度通量即向上输运起主导作用.同时浓度通量在不同相位变化显著,其演化状态与法向湍流强度具有一致性.当t/T=4/8,5/8 时,法向速度脉动的增强伴随着浓度通量的增大.当t/T=6/8,浓度通量大幅度地增加,随后在t/T=7/8 相位点减弱.说明法向湍流脉动在污染物溶质从沉积层往上覆水释放过程中发挥重要作用.综合图7 可以判断在相位t/T=4/8,5/8 扩散子区成为更强的传质限制层,但在相位t/T=6/8,7/8 部分含能涡能够突破限制主导质量输送.

图7 A=45°,T=12算例在x-z平面 y+=103 处法向速度脉动的等值线图(v′=±2.0)Fig.7 Contour plot of the instantaneous wall-normal velocities(v′=±2.0) parallel to the x-zplane (y+=103) for the A=45°,T=12case

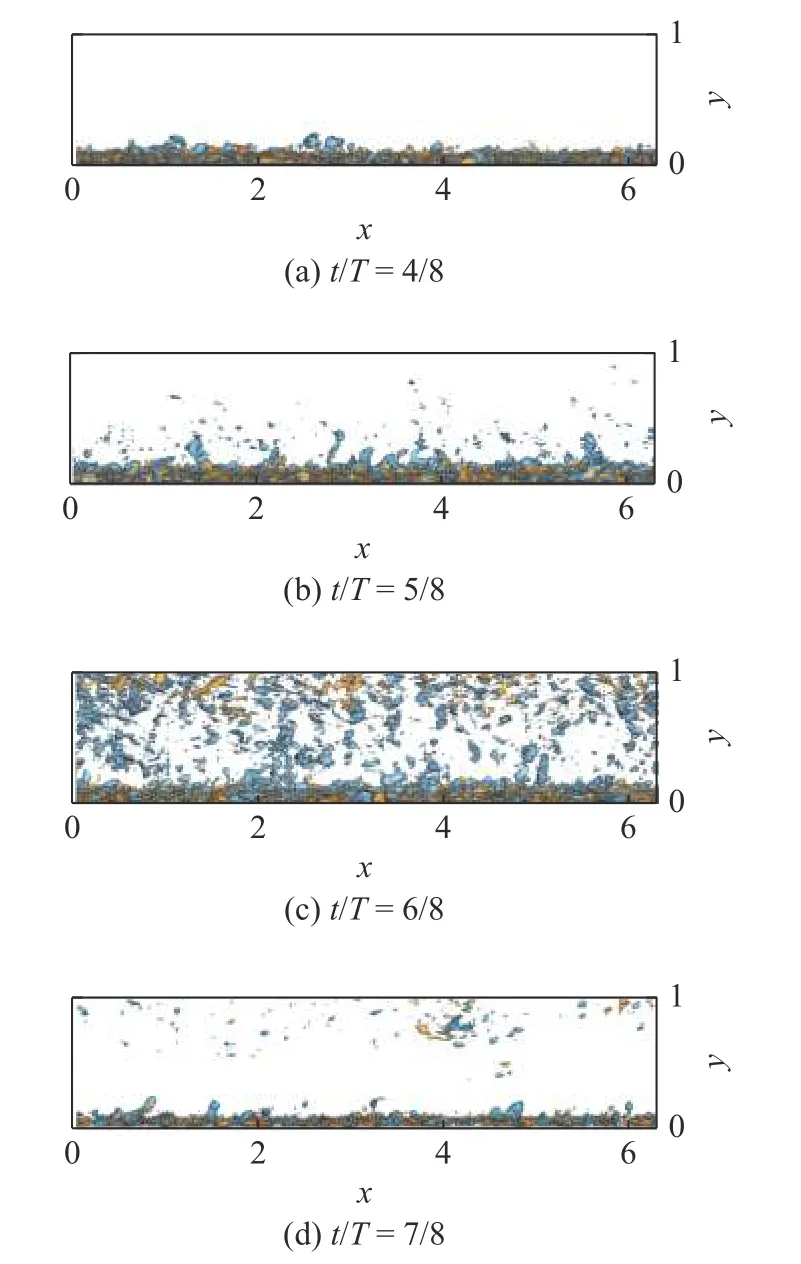
图8 算例 A=45°,T=12 在不同相位的法向浓度通量瞬时等值面分布图(z方向视图).蓝色和棕色分别代表法向浓度通量值为C′v′=0.01和C′v′=-0.01Fig.8 Contour maps of the instantaneous wall-normal convective concentration flux in different phases for A=45°,T=12 (z-direction view).The blue and the brown iso-surface means C′v′=0.01 and C′v′=-0.01

2.2 振荡角和振荡周期对平均速度和浓度的影响

从上覆水流场到其下高渗透沉积层的高Schmidt数传质行为受制于近SWI 界面处湍流的主要特性,包括黏性底层和扩散子区的流动特性.图9(a)给出流向平均速度沿法向的分布.需要注意的是各图中出现的竖直细虚线表示沉积层和水层交界面SWI(y=0.1或y+=52).当展向振荡驱动力占优时,即A=75°,长周期振荡导致水层流向速度明显减小.而当流向振荡驱动力占优时(A=15°),则流向速度均维持较高水平.

图9(b)给出平均浓度沿法向分布.可以看出,当振荡周期较大时,无论A=15°还是A=75°,沉积层中污染物释放速率加快,使得上覆水中的浓度水平更高,表2 中的〈Cw〉也反映了相同的结果.原因在于SWI 处速度梯度增大,该处剪切应力和摩阻增大.说明振荡驱动力主导下有利于突破扩散子层限制增强在沉积层上下的动量和质量交换,导致污染溶质更易于向上释放和扩散.

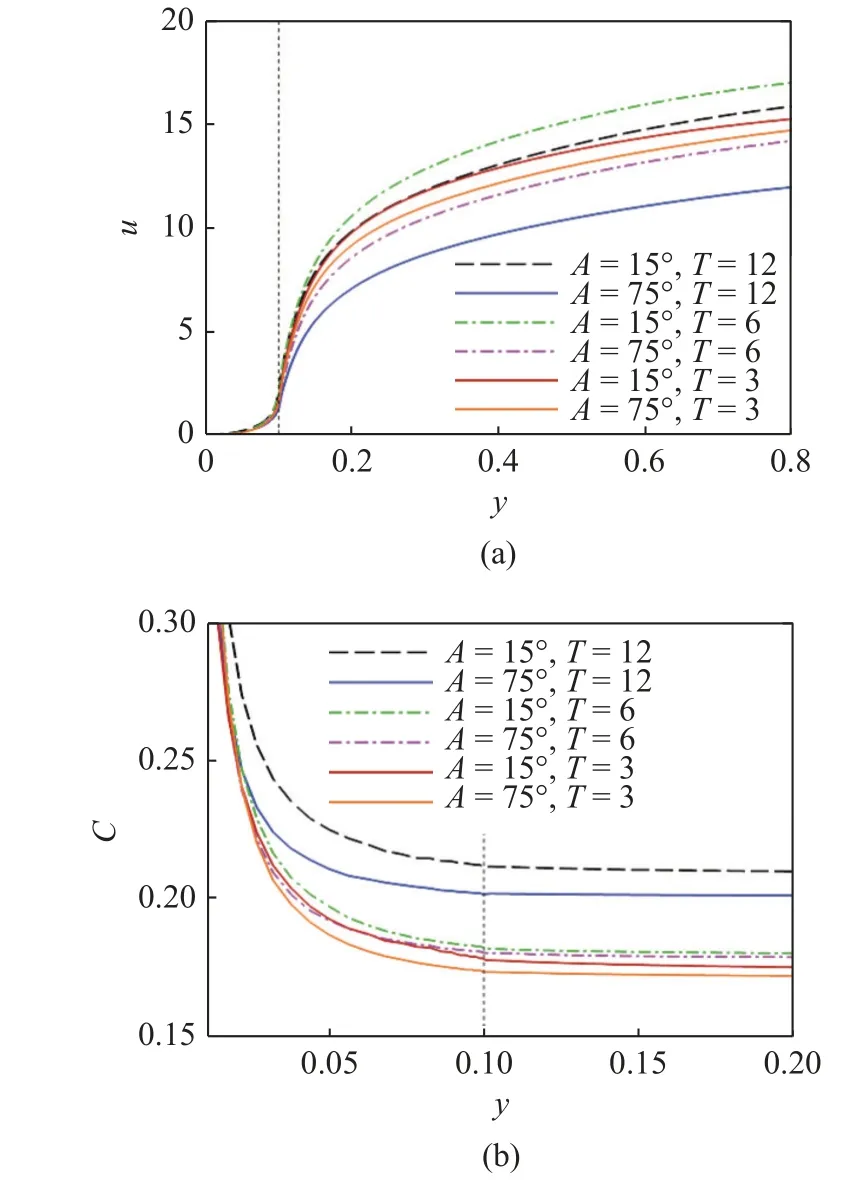
图9 (a)流向平均速度和(b)平均浓度沿法向分布Fig.9 (a) Mean streamwise velocity and (b) mean concentration distribution along the normal direction

进一步,采用象限分析法考察了振荡过程中如湍流猝发事件在动量传递和污染物输运过程中所起的作用.图10 统计了雷诺应力的变化.其中图10(a)和图10(b)分别是第二象限的上抛运动(u′＜0,v′＞0)和第四象限的下扫运动(u′＞0,v′＜0).可以看出,当振荡角减小或周期增大时,SWI 之上流动的上抛下扫行为随之增强,且上抛强于下扫.结合前面图7 和图8 的分析,可知污染物上扬事件与猝发事件的关联性.这再次表明了沉积层中污染物释放速率加快,导致上覆水中高浓度水平的内在原因.

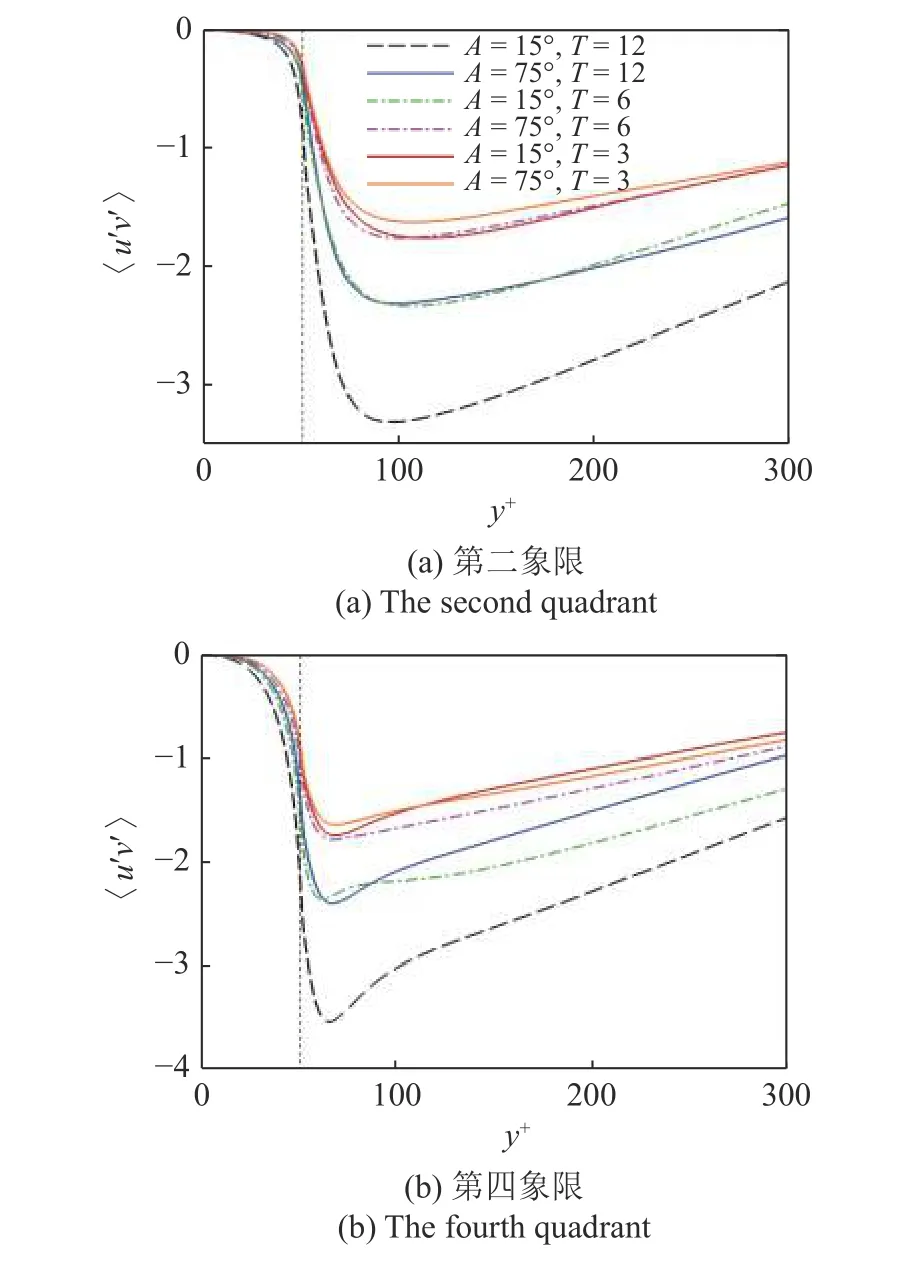
图10 雷诺应力在第二、四象限的分布Fig.10 Distribution of Reynolds stress in the second and fourth quadrants

图11(a)给出了不同振荡条件下湍流诱导的浓度通量沿法向分布.可以发现,随着周期增大,浓度通量增大.当周期较小时(T=3),浓度通量对振荡角的变化不敏感.而当周期较大时,随着振荡角减小,法向通量也随之增大.值得注意的是,SWI 上方的浓度通量并非线性递减,而是会在y+=150 处出现再次增高现象,这源自于该处法向速度脉动强度最大,如图11(b)的y=0.3 处.以较低频率进行的流向或展向振荡会显著提高法向浓度通量,促进污染物向上覆水中迁移扩散.

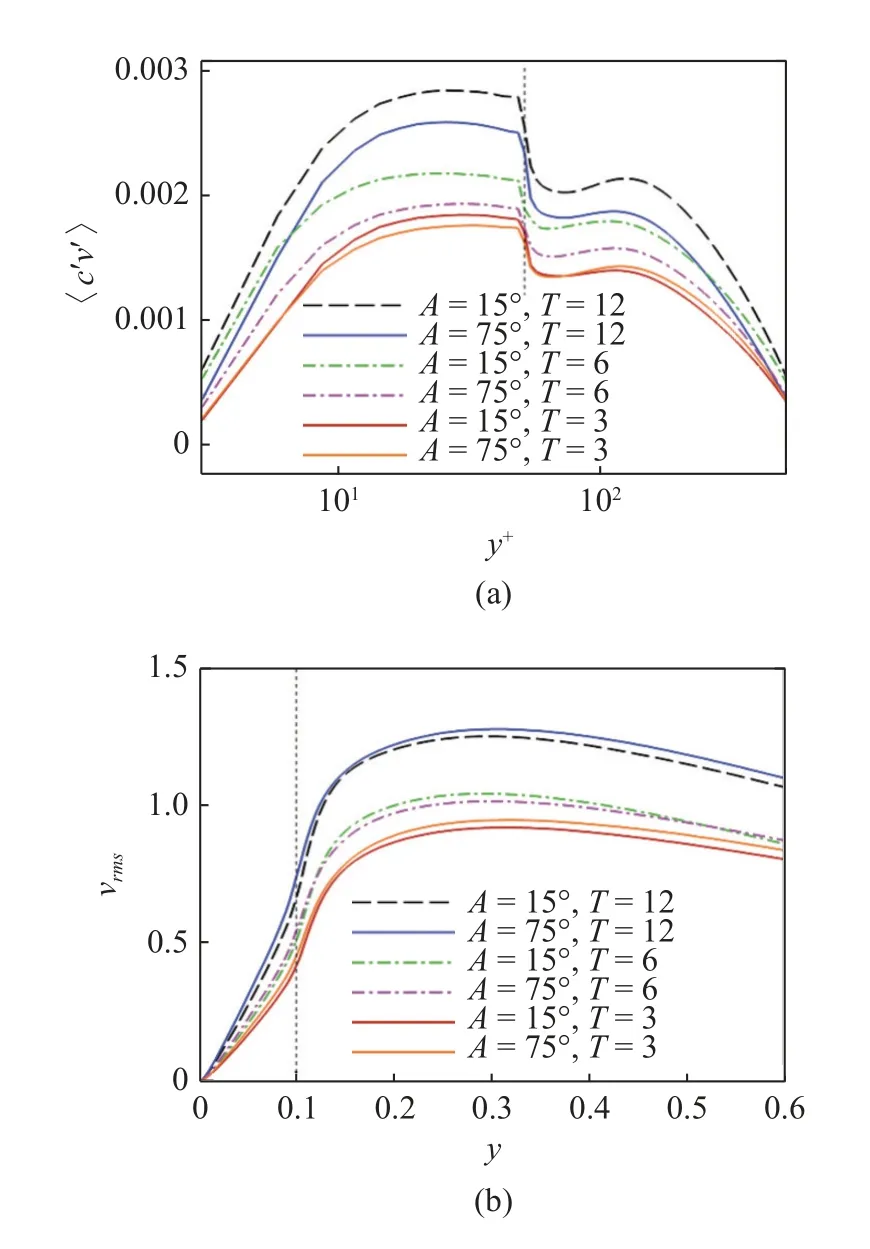
图11 (a)浓度通量和(b)法向湍流强度沿法向分布Fig.11 Distribution of (a) concentration flux and (b) turbulent intensities along normal direction

在自然水环境系统中,由多种不同尺度且相互作用的水动力机制共同驱动着SWI 区域的物质交换,这些机制包括分子扩散、对流扩散和湍流渗透,而有效扩散系数能够综合反映多种机制的共同作用[33].从表2 中可以得知,随着振荡周期增大,当流向驱动力占优时,分子扩散通量增大;而当展向驱动力占优时,分子扩散通量减小,说明其浓度输运的增强主要来自于湍流作用.值得注意的是,当T=12时,由于流向速度出现了间歇性的回流(图4(b)的流向速度Ub出现负值),导致SWI 上方产生较大的湍流通量.

当渗透率较高时,湍流通量是在质量输运中占主导地位的,而随着周期增大,SWI 处的湍流通量增大.在此定义有效扩散率为分子扩散通量与湍流通量之和与分子扩散通量的比值,表达式为

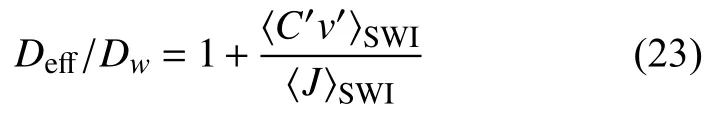
图12 统计了不同振荡角和振荡周期下的有效扩散系数的分布情况,图中横坐标为振荡角,纵坐标为SWI 处的有效扩散率.从整体趋势来看,随着振荡角或振荡周期增大,扩散率随之增大.而当振荡驱动力逐渐过渡到以展向为主时,较长的振荡周期对扩散率的增幅影响更大.

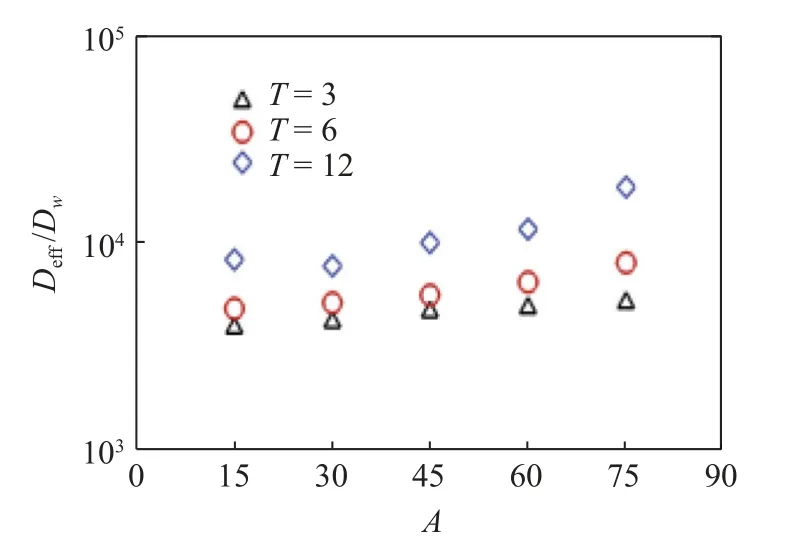
图12 不同振荡角和振荡周期与有效扩散系数的关系Fig.12 Relationship between different oscillation angles and oscillation periods and effective diffusivity

3 结论

本文通过大涡模拟研究了有振荡激励下沉积层内外湍流流动特性、相干结构、猝发现象、统计特性和污染物输运特性.对不同振荡角与振荡周期下的平均湍流强度、污染物溶质浓度分布、通量变化和瞬态结构进行了分析,得到结论如下.

(1)周期性振荡驱动作用导致了体积平均的流向、展向速度、湍动能以及沉积层内污染物浓度呈现与振荡角和振荡周期直接相关的准周期性变化,且与振荡驱动力存在不同的相位差,表明速度场和浓度场对振荡驱动力的变化有着不同程度的时间延迟响应.

(2)当展向振荡驱动力强于流向振荡时,随着振荡周期增加,平均湍动能以及沉积层内污染物浓度波动幅度增大.由于SWI 处流体的上抛强于下扫,进而以对流扩散方式作用于浓度标量.此处有效扩散率增大,污染物溶质向水层中输运增强,表明展向振荡流与污染物浓度输运的波动的关联性更强.

(3) SWI 界面的浓度通量变化与法向速度脉动具有明确的相关性.较低频率和展向振荡为主的双重条件会强化湍流混合,显著提高有效扩散率.研究还证实SWI 处污染物上扬事件与湍流猝发事件的一致性,表明猝发行为在上扬过程中有效推动其中的物质输送和交换.