苏南区块中子-密度交会计算孔隙度方法应用
2022-11-06王亚兰杨凯程王河向晓潘晓丽薛媛竹
王亚兰,杨凯程,王河,向晓,潘晓丽,薛媛竹
(1.中国石油集团测井有限公司长庆分公司,陕西西安 710200;2.中国石油长庆油田苏里格南作业分公司,陕西西安 710018;3.中国石油长庆油田分公司第一采气厂,陕西西安 710021)
1 地质概况
苏里格南区块位于鄂尔多斯盆地的苏里格气田中区南部,区域构造位于伊陕斜坡北部,区块面积2 393.4 km2。晚古生代是本区含气的重要层系,自下而上发育石炭系本溪组、二叠系太原组、山西组、石盒子组和石千峰组,其中山西组山1 段、石盒子组盒8 段为主要含气层段,分别为曲流河和辫状河沉积。
二叠系砂岩主要有3 种类型:石英砂岩、岩屑石英砂岩、岩屑砂岩,盒8 段以石英砂岩为主,岩屑石英砂岩次之,岩屑砂岩较少。山1 段则岩屑石英砂岩所占比例高,石英砂岩次之。盒8 段储层孔隙度主要分布在5.0%~14.0%,平均8.97%;渗透率在0.1~1.0 mD,平均0.46 mD。山1 段储层孔隙度一般在5.0%~14.0%,平均6.5%;渗透率在0.1~0.5 mD,平均0.25 mD。总体上看,属于典型的低孔、低渗砂岩储层。
2 中子-密度交会计算孔隙度方法应用背景
苏里格气田沉积和成岩的强非均质性使不同砂组、小层之间岩性、电性、物性和含气性关系差别较大,孔渗关系复杂,加上苏南区块取心资料少,给测井解释带来许多困难。孔隙度是反映储层地质特征的一个重要参数,准确计算孔隙度也是准确计算含水饱和度、渗透率等其他储层参数的前提[1-2]。多年来苏里格气田上古生界测井解释都是应用常规的单声波时差计算储层孔隙度,苏南公司经过相关研究和对比分析,发现用中子-密度曲线交会方法计算的孔隙度与岩心分析孔隙度更加吻合,较单声波时差计算的孔隙度更能真实反映低-特低孔储层的孔隙度。
3 三孔隙度计算方法及影响因素
3.1 计算方法
声波时差、密度、补偿中子是三种常规的孔隙度测井曲线。受测井原理影响,这三种测井方式在反映储层孔隙度方面有所不同。
声波时差测井是记录声波在地层中传播l m 所需要的时间。它与岩石骨架成分、孔隙度的分布和孔隙中流体的性质有关。对于固结并压实的粒间孔隙度、纯砂岩的孔隙度用下面的威里公式计算:
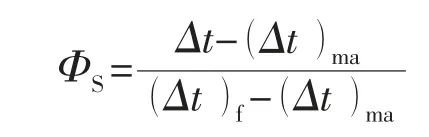
式中:ΦS-声波孔隙度;Δt-地层声波时差测井值;(Δt)ma-地层骨架声波时差;(Δt)f-地层中流体声波时差。
密度测井是用伽马源发射的伽马射线照射地层,根据康普顿效应测量地层体积密度的测井方法[3]。利用地层中电子密度与其真实体积密度的线性关系来计算密度孔隙度。其计算公式是:
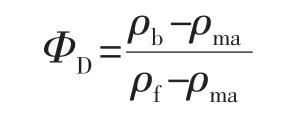
式中:ΦD-密度孔隙度;ρb-地层体积密度测井值;ρma-地层骨架密度;ρf-地层中流体密度。
中子测井是利用岩石对中子的减速与俘获过程,在井下用中子源向地层发射连续的快中子流,这些快中子与地层的元素产生核碰撞而使中子能量损失并减速。氢是最强的减速剂,而储集层中常见的岩石(砂岩、石灰岩、白云岩及混合岩性)其矿物成分不含氢,岩石的含氢量基本上分布在岩石孔隙的流体中,即水和油气中。因此,中子测井反映的是岩石中充满流体的孔隙度。其计算公式是:
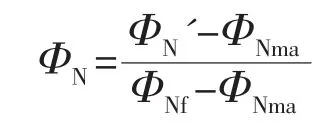
式中:ΦN-中子孔隙度;ΦN'-地层中子测井值;ΦNma-地层骨架中子孔隙度;ΦNf-地层中流体中子孔隙度。
3.2 影响因素
岩石在形成过程及后期作用中,造成的粒间(晶间)孔隙、裂缝及洞穴等,称岩石孔隙。根据孔隙流体在孔隙中能否运动的状况,孔隙可分为总孔隙和有效孔隙。总孔隙是指岩石中所有孔隙空间的总体,不论其孔隙的大小、形状以及是否连通;有效孔隙是指互相连通且在一般压力条件下流体可以在其中流动的那部分孔隙。根据孔隙成因,孔隙可分为岩石成岩过程中形成的原生孔隙(岩石基块孔隙度)和成岩后期作用中形成的次生孔隙(裂缝或溶蚀孔隙度)。岩石孔隙体积与岩石总体积之比称孔隙度[4]。
对于砂泥岩地层,如果是纯水层、地层压实程度较高且没有次生孔隙的情况下,利用任何一种单孔隙度测井数据都可以得到较精确的孔隙度计算结果。但是对于含有天然气或轻质油的地层,且地层疏松压实程度不高的情况下,单条曲线求孔隙度均有其弊病,利用上述孔隙度计算公式,三条孔隙度曲线所提供的孔隙度都是总孔隙度(有效孔隙和束缚水孔隙),均不能反映真实的地层孔隙度。而在评价储层的含油气能力时,用的均是储层的有效孔隙度。在纯地层,总孔隙度等于有效孔隙度;在含泥质地层,需要对泥质影响进行校正来得到有效孔隙度。
根据苏里格南区块13 口井129 块样品统计表明:盒8、山1 段储集层主要发育四类孔隙:原生粒间孔隙、次生溶孔、晶间孔和粒间孔。其中原生粒间孔隙在孔隙构成中居于次要地位,孔隙类型以次生溶孔和高岭石晶间孔为主。而声波测井只能反映原生孔隙度,无法反映次生孔隙度。声波时差受泥质分布、油气和地层压实程度的影响都比较大。多年来苏里格气田上古生界测井解释都是应用常规的单声波时差计算储层孔隙度,计算孔隙度的公式是来自相邻区块岩心数据和测井数据做相关分析得到的回归公式。根据测井原理,在泥质含量较高的地层中,由于泥质疏松的特性会增加声波在地层中的传播时间,导致声波时差增大,会使声波计算孔隙度的结果比实际地层孔隙度偏大。
中子、密度测井不受泥质分布和压实程度的影响并能够反映次生孔隙,而且对泥质和天然气(或轻质油)的影响反映灵敏,能够较好的作泥质校正和油气校正。用中子密度交会计算孔隙度相对比较准确。
3.3 三孔隙度测井曲线气层响应特征
当地层中含有天然气时会对三种孔隙度测井值产生影响,三条孔隙度测井曲线在气层的一般响应特征如下所示。
(1)声波曲线(AC):由于天然气会导致声波幅度的衰减和传播速度的降低,因而气层在声波测井曲线上呈现出周波跳跃或声波时差增大的现象。
(2)密度曲线(DEN):密度测井响应于地层的电子密度(或体积密度),电子多说明岩石密度较大,如果地层孔隙中含气,则由于气体的低密度影响,使地层体积密度降低,密度孔隙度增大。
(3)中子曲线(CNL):中子孔隙度测井响应于地层的含氢指数,由于天然气的含氢指数与体积密度比油或水小得多,另外挖掘效应也增强了这种效果,因此中子测井在气层处呈现低值[5-6]。
4 中子密度交会计算孔隙度方法
4.1 计算原理
在岩性和孔隙度定量评价中,岩石内除含有不同性质的流体之外,根据岩石骨架成分数目,常见有以下几种情况:单矿物纯地层(不含泥质)、单矿物含泥质地层、双矿物纯地层(不含泥质)、双矿物含泥质地层、三矿物纯地层(不含泥质)、三矿物含泥质地层,苏南区块目的层主要为单矿物含泥质地层。
孔隙度测井的体积密度、声波时差和含氢指数所表征的物理过程如康普顿散射、声波的传播以及中子的减速和吸收,都是体积效应。因此在研究这些过程有关的测井响应方程时可采用“体积模型”概念。所谓“岩石体积模型”就是根据岩石的组成,按照物理性质(如声波、密度或中子测井孔隙度等)差异,把单位体积岩石分成对应的几部分,然后研究每一部分对测量结果的贡献,并把测量结果看成是这几部分贡献的综合。
苏南目的层段地层主要为单矿物(砂岩骨架)含泥质地层,即岩石体积模型包括流体、砂岩骨架和泥质三部分,所以声波时差、补偿中子和密度测井的响应方程分别为:
Δt=ΦΔtf+VsandΔtsand+VshΔtsh
ΦN=ΦΦNf+VsandΦNsand+VshΦNsh
ρb=Φρf+Vsandρsand+Vshρsh
且有Vsh+Vsand+Φ=1(物质平衡方程)
其中:Δt、ΦN和ρb分别为声波时差、补偿中子和密度测井的实际测量值;Δtf、ΦNf和ρf分别为地层流体的声波时差、补偿中子和密度值;Δtsh、ΦNsh和ρsh分别为纯泥岩的声波时差、补偿中子和密度值;Δtsand、ΦNsand和ρsand分别为纯砂岩的声波时差、补偿中子和密度值;Vsh为泥质含量,Φ 为孔隙度,Vsand为砂岩含量。
4.1.1 联立测井响应方程组求解 在地层流体、纯泥岩以及岩石骨架等参数和泥质含量已知的情况下,结合物质平衡方程利用中子-密度孔隙度测井资料确定岩性和孔隙度的方程组,即为:
ΦN=ΦΦNf+VsandΦNsand+VshΦNsh
ρb=Φρf+Vsandρsand+Vshρsh
Vsh+Vsand+Φ=1
对上述方程组求解,即可得到Vsh、Vsand和Φ。
4.1.2 交会图法确定岩性和孔隙度 交会图法实际上就是测井响应方程组的图解形式,首先根据测井响应方程组和相关参数建立解释图版,然后根据解释层段的数据点落在图版上的位置读取泥质含量和孔隙度,该方法直观、简捷,并方便于处理过程中泥岩参数的选取,而且也适用于手工快速估算泥质含量和孔隙度值。
根据流体的补偿中子和密度值(流体点F)、纯砂岩补偿中子和密度值(骨架点M)以及纯泥岩补偿中子和密度值(泥岩点C)构成解释三角形(图1)。

图1 中子-密度交会图
流体点和骨架点的连线为纯砂岩线MF,骨架点M 处孔隙度为0,流体点F 处孔隙度为100%。在纯砂岩线MF 上从0~100%按等间距分割成不同的孔隙度刻度。
泥岩点与骨架点连线为泥岩线MC,骨架点M 处泥质含量为0,泥岩点C 处泥质含量为100%。在泥岩线MC 上从0~100%按等间距分割成不同的泥质含量刻度。
在纯砂岩线MF上,经过不同的孔隙度刻度,在三角形内做平行于泥岩线MC 的平行线;在泥岩线MC上,经过不同的泥质含量刻度在三角形内做平行于纯砂岩线MF 的平行线,在三角形内形成不同孔隙度和泥质含量的网格。
根据解释层段的数据点落在图版上的位置即可同时读取泥质含量和孔隙度。
如果地层孔隙中含气,由于气体的低密度影响,使地层体积密度降低,密度孔隙度增大。含气砂岩由于天然气的挖掘效应,会使地层的中子孔隙度降低。
因此在中子密度交会图上,含气的资料点将落在含水纯砂岩线的左上方。天然气影响越大,气层的点就越向左上方移动。如果将ρb与ΦN的曲线重叠,会以ρb≥ΦN的特征显示气层[7]。
4.2 应用效果分析
苏南区块共有SNXXX1、SNXXX2、SNXXX3 三口取心井,将这三口井的岩心分析孔隙度分别与声波时差计算的孔隙度以及中子-密度交会方法计算的孔隙度进行对比,发现在泥质含量较高的地层,声波时差计算的孔隙度比岩心分析孔隙度偏大,中子-密度交会计算的孔隙度与岩心分析孔隙度更加吻合。
岩心孔隙度分别与中子密度和声波计算的孔隙度进行相关性分析的结果见图2、图3。从图上可以看出,中子密度孔隙度与岩心孔隙度的相关系数为0.823,而声波孔隙度与岩心孔隙度的相关系数为0.735,中子-密度交会计算的孔隙度更加接近岩心孔隙度,较单声波时差法计算的结果相关系数提高了12%。
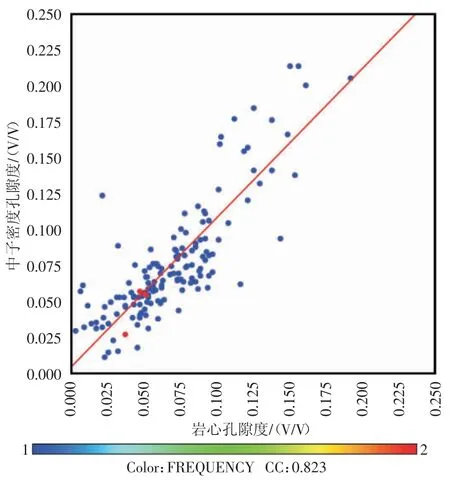
图2 岩心孔隙度与中子密度孔隙度交会图
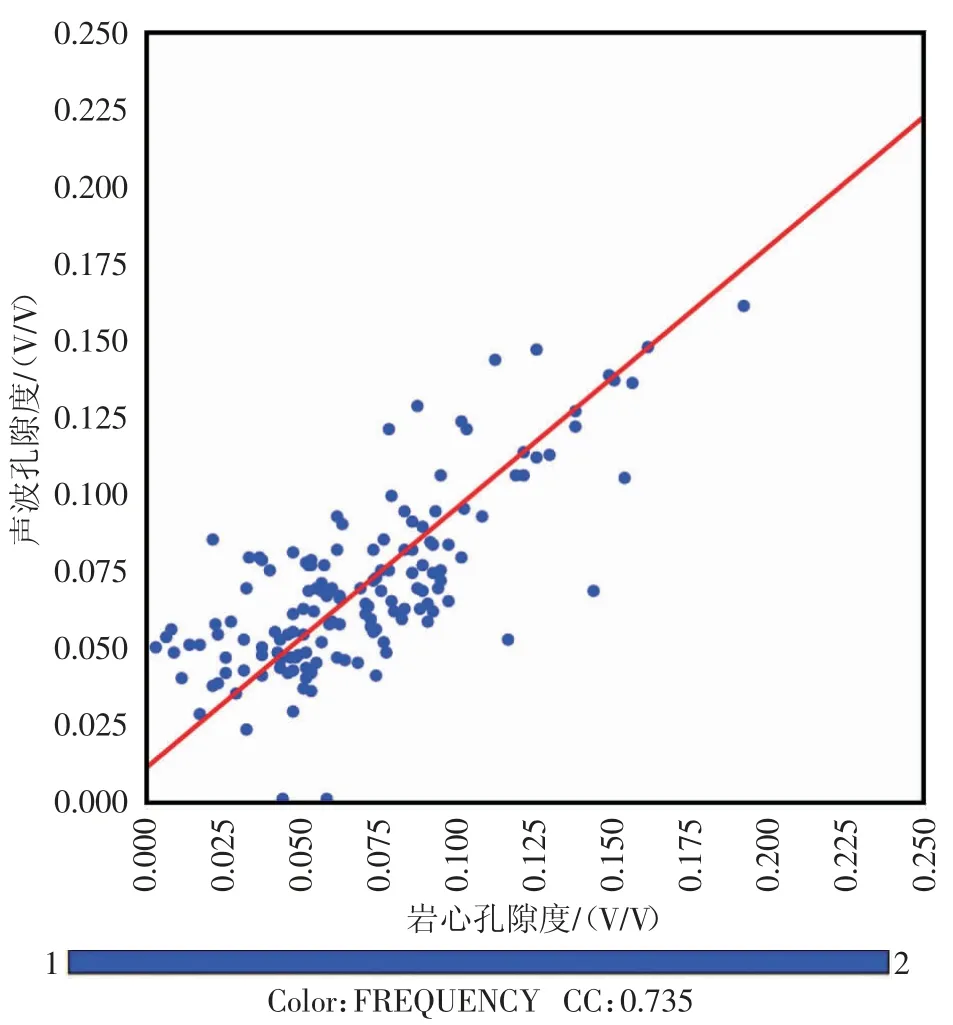
图3 岩心孔隙度与声波孔隙度交会图
由于声波时差计算的孔隙度比岩心分析孔隙度偏大,代入含气饱和度公式计算时,也会相应的使含气饱和度计算结果偏高而导致解释结果过于乐观,利用声波孔隙度计算的含气指数也会偏大,在利用含气指数进行压裂层段选择时,这些误差可能会导致非有效储层被压裂,增加生产成本,并影响地层静态资料与生产动态资料的符合度。
由图4 可知,SNXXX4 井第38、41 和46 号层,声波时差计算的孔隙度较高是由于泥质含量较高导致,并非好的储层,但是根据孔隙度和含水饱和度的计算结果,本井有5 层17.2 m 砂层为气层和差气层,平均孔隙度为8.3%,为物性较好的储层。看起来压裂层段较厚,储层物性较好,但压裂后无阻流量不到5×104m3/d,与测井解释结果明显不符。
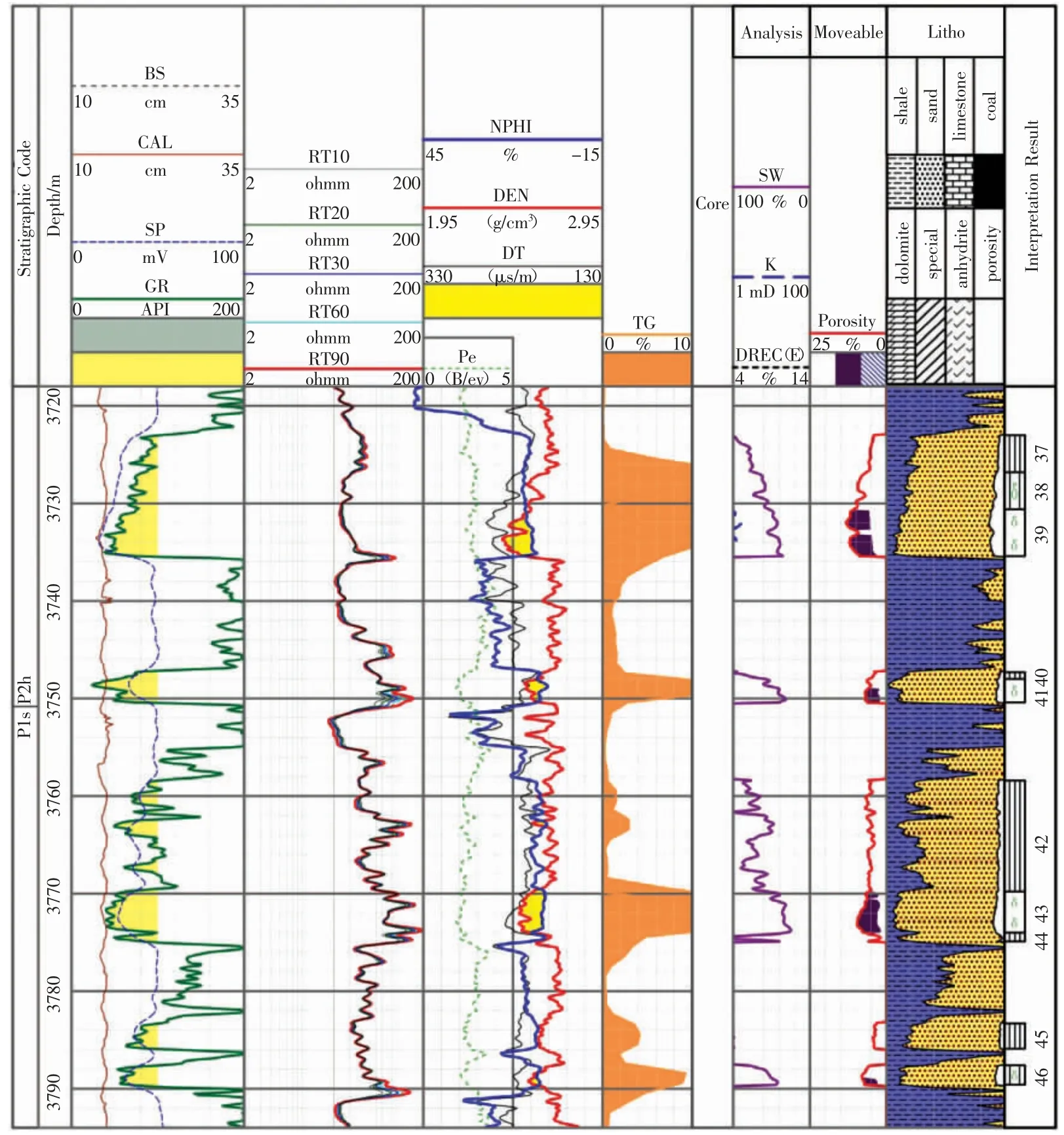
图4 SNXXX4 井测井综合图
通过对苏南区块2011 年以来所有同时测量了声波和中子、密度曲线并进行了压裂试气的井计算了压裂段储层的含气指数,最终每口井都得到了I_SON 和I_ND 两个含气指数(I_SON 为声波孔隙度计算的含气指数,I_ND 为中子-密度交会孔隙度计算的含气指数,含气指数越大,意味着单位体积的地层含气越多)。选取稳定的无阻流量AOF 为标准,分别与I_SON 和I_ND 进行相关性分析,I_SON 与AOF 的相关系数为0.468,而I_ND 与AOF 的相关系数为0.608,后者比前者相关系数提高了30%(图5、图6)。
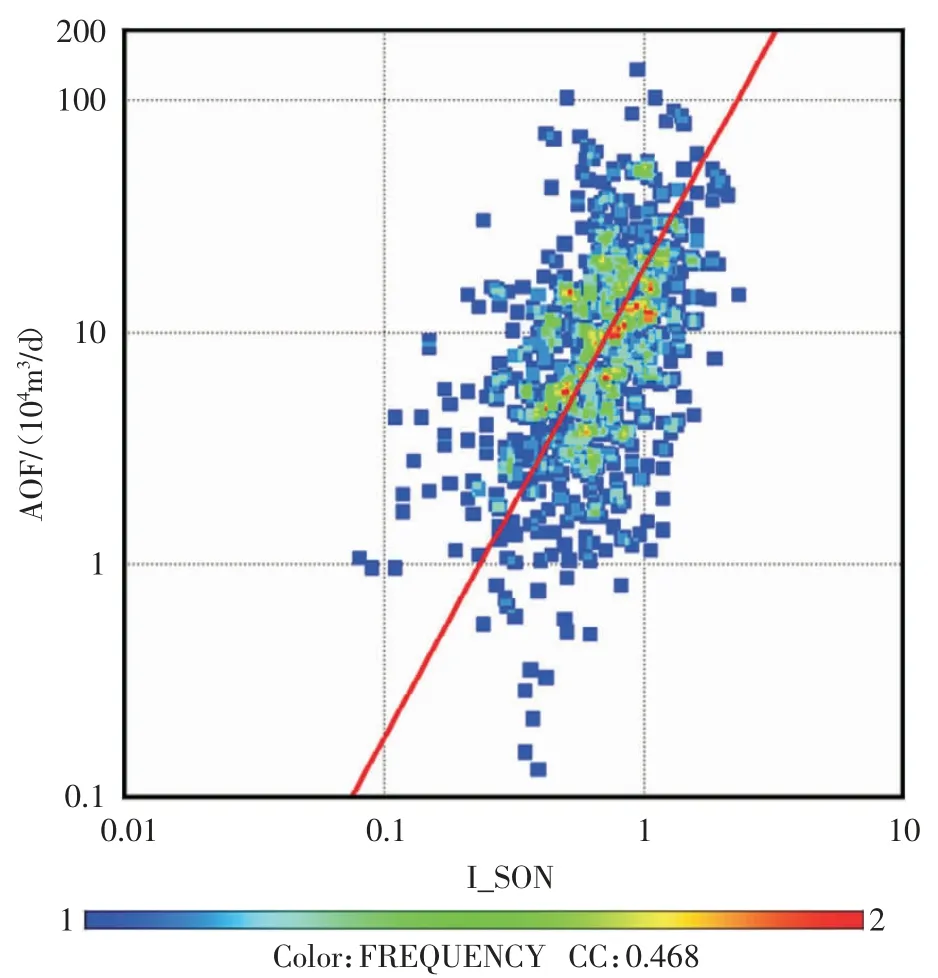
图5 I_SON 与无阻流量相关性分析
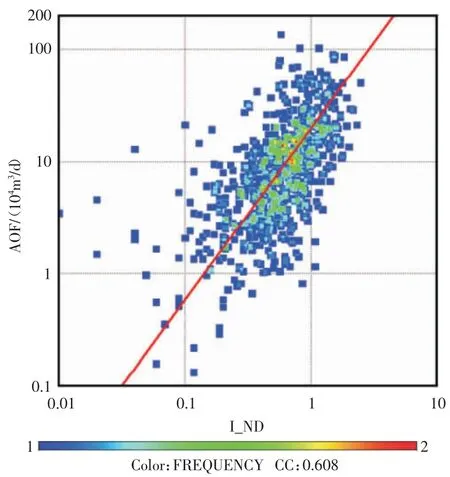
图6 I_ND 与无阻流量相关性分析
可见利用中子-密度交会孔隙度计算的含气指数比利用声波孔隙度的计算结果更能准确地反映储层的含气性和生产能力,能够为压裂层段的选取提供更加有效的依据,从而优化压裂段选取,最大可能地选取有效储层进行压裂试气,提高动静态数据符合度。
5 结论
(1)通过对三孔隙度计算方法的影响因素和原理的分析,以及三口取心井的岩心分析孔隙度与声波时差计算的孔隙度和中子-密度交会方法计算的孔隙度进行对比,证实声波时差计算的孔隙度比岩心分析孔隙度偏大,中子-密度交会计算的孔隙度与岩心孔隙度的相关系数为0.823,更加接近岩心孔隙度,较单声波时差法计算的结果相关系数提高了12%,计算结果可以真实反映低-特低孔储层的孔隙度。
(2)中子-密度交会孔隙度计算的含气指数和用声波孔隙度计算的含气指数相比更能准确地反映储层的含气性和生产能力,前者与稳定的无阻流量AOF 的相关系数比后者提高了30%,能够为压裂层段的选取提供更加有效的依据,避免压裂无效井段,提高了动静态数据符合度。
