带限周期函数的Fourier 插值法在天线测量中的应用

付煜洲 杨佳蔚 王朕 商锋

（1. 西安邮电大学电子工程学院,西安 710121；2. 广东曼克维通信科技有限公司,广州 510700；3. 西安空间无线电技术研究所,西安 710000）

引 言

现有的天线测量方法一般可分为远场测量[1]和近场测量[2].近场测量是在微波暗室内，利用计算机控制一个特性已知的探头，抽测出距离天线表面3～5 个波长的某个表面上场的幅度和相位分布，然后由近场测量数据、探头特性和扫描面的形状，通过近远场变换算法计算出天线的远场特性[3].根据扫描面的形状，天线近场测量一般分为平面近场测量[4]、柱面场测量[5]和球面场测量[6].近场测量能够得到天线远场的三维方向图数据，但系统成本高且测量时间长，误差源较多[7-8].如只需要得到某一切面的方向图数据，且场地条件满足天线远场距离，往往采用远场法对天线进行测量.远场测量因测试方法简单、直观，设备简单，测试成本相对较低，能很快得到天线某一切面测试结果，成为天线测试的首选.

对具有高增益、窄波束特点的常用天线(例如阵列天线、反射面天线等)采用远场测量时，采样间隔往往要求小于待测天线3 dB 波束宽度的1/10[9].增大采样间隔导致测量到的半功率波束宽度、副瓣电平等天线辐射参数不准确，造成测量误差；减小采样间隔会降低测试效率，尤其在多通道、多波束、扫频测量中测试效率会显著降低.

针对远场测量效率低下的问题，本文给出了一种基于带限周期函数的Fourier 插值法，采样间隔相同的情况下仍然能够显著提高测试效率，得到的远场方向图角度间隔理论上可以任意小.仿真及实测结果表明，应用此方法插值后得到的远场结果与实际远场结果吻合非常好.

1 算法基本原理

周期为T的复值函数f(t)的Fourier 级数为

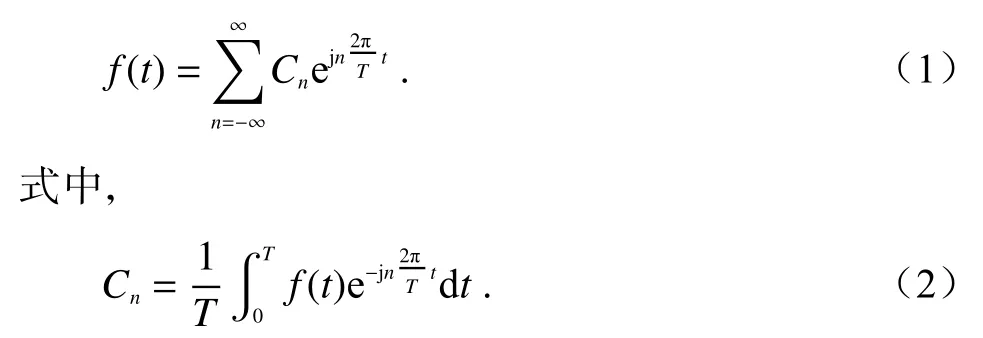
若存在有限的正整数N，使得当 |n|＞N时，Cn=0，即f(t)的最高谐波分量为，则称f(t)为带限周期函数，f(t)可表示为

当f(t)为带限周期函数时，可以通过一个周期内若干个离散点的函数值来计算[10-11]，分析如下：

式(1)中取t=mT/J(m=0,1,···,J-1)，则有

命l=n+rJ，n=0,1,···,J-1;r=-∞,···,0,···,∞；则式(4)变为

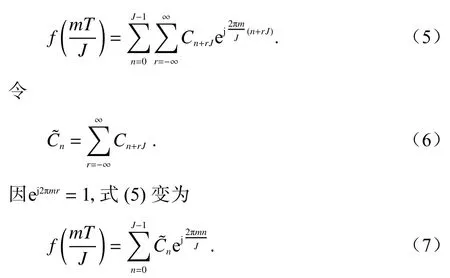
式(7)实际上是一个离散Fourier 变换的形式，可以表示为

只需知道f(t)在一个周期内间隔J个点的函数值，就能精确求出Fourier 展开系数(n=0,···,J-1).

取样点数J满足J≥2N+1，Cn=0,|n|＞N时，Cn与有如下关系[12]：

将Cn代入式(3)，得到密度任意高的f(t).取t=mT/L(m=0,1,···,L-1)，L越大，密度越高，且可以用逆快速Fourier 变换计算.

由于场的单值性，天线方向图f(φ)是 以 2π为周期的复值函数，且是带限的[13-15]，即：

式中：N由天线尺寸和坐标原点的位置决定[16]，一般取2～10，λ 为工作波长，ρmin是以坐标原点(测量时天线转台的转动中心)为中心作一个完全能够包围待测天线的最小圆柱的半径，若坐标原点选在天线的几何中心，则 ρmin为天线最大尺寸的1/2.

|f(φ)|为 幅度方向图，常用 20lg(|f(φ)|)(dB)表示；ang(f(φ))表 示相位方向图.f(φ)的 带限为N，|f(φ)|带限为2N.因此，由插值前的幅度方向图恢复待测天线幅度方向图时，式(3)、(8)～(10)中的N变为N′即可.

2 结果分析

2.1 数值仿真验证

数值仿真中选取单元数目Ne=20，排列为如图1所示的线阵，阵列幅度为-30 dB 的Taylor 分布，单元间距d=0.6λ.每个单元由两个半波振子组成，为实现单向辐射，两个振子x轴方向相距 λ/4，第n个单元后振子的激励电流为In，前面振子的激励电流为Ine-jπ/2，坐标原点取后排振子中心.该天线阵xoy面的理论方向图函数可以表示为

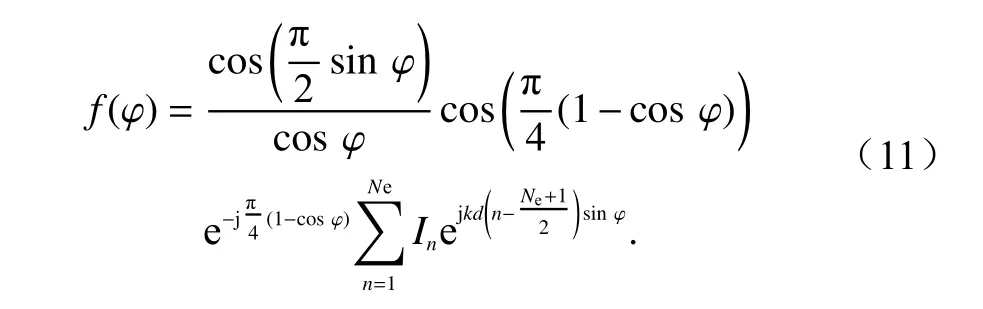
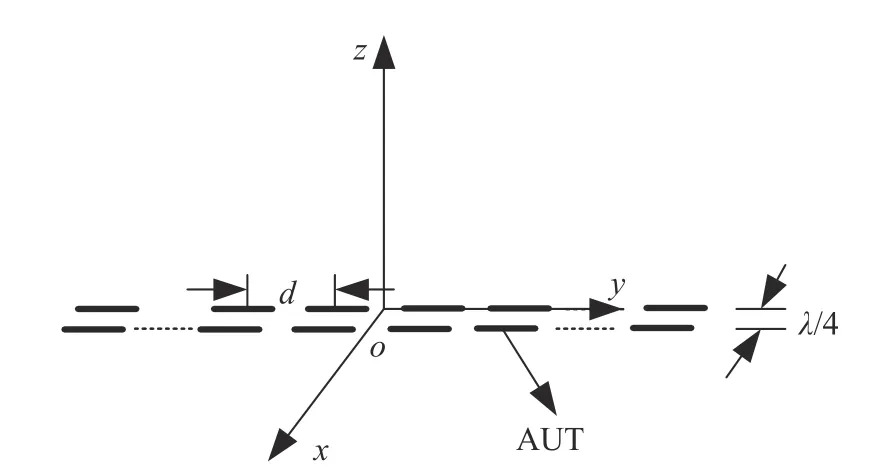
图1 天线模型Fig.1 The antenna model

天线模型3 dB 波束宽度约为5.3°，因此远场测量时，传统采样间隔应在0.5°以下.应用本文方法，≈6λ，N0=8，则N=+8=46，J=2N+2=94，测量的角度间隔 dφ=

图2 为采样间隔为 dφ的幅度方向图与相位方向图.可以看出，此时方向图因角度间隔太大，不能显现方向图细节，天线的半功率波束宽度、副瓣电平等天线辐射参数难以评估.用基于带限周期函数的Fourier插值法求出角间隔为360°/4 096 的方向图数据，与式(11)直接计算得到的幅度和相位方向图进行比较，结果如图3 所示.可以看出：应用本文方法得到的插值后幅度方向图与理论方向图吻合较好；插值后的相位方向图与计算得到的相位方向图不完全重合的地方幅度为0，由于振幅为0 相位任意的复数值仍为0，因此并无影响.

图2 插值前仿真幅度和相位方向图Fig.2 The amplitude and phase patterns before interpolation

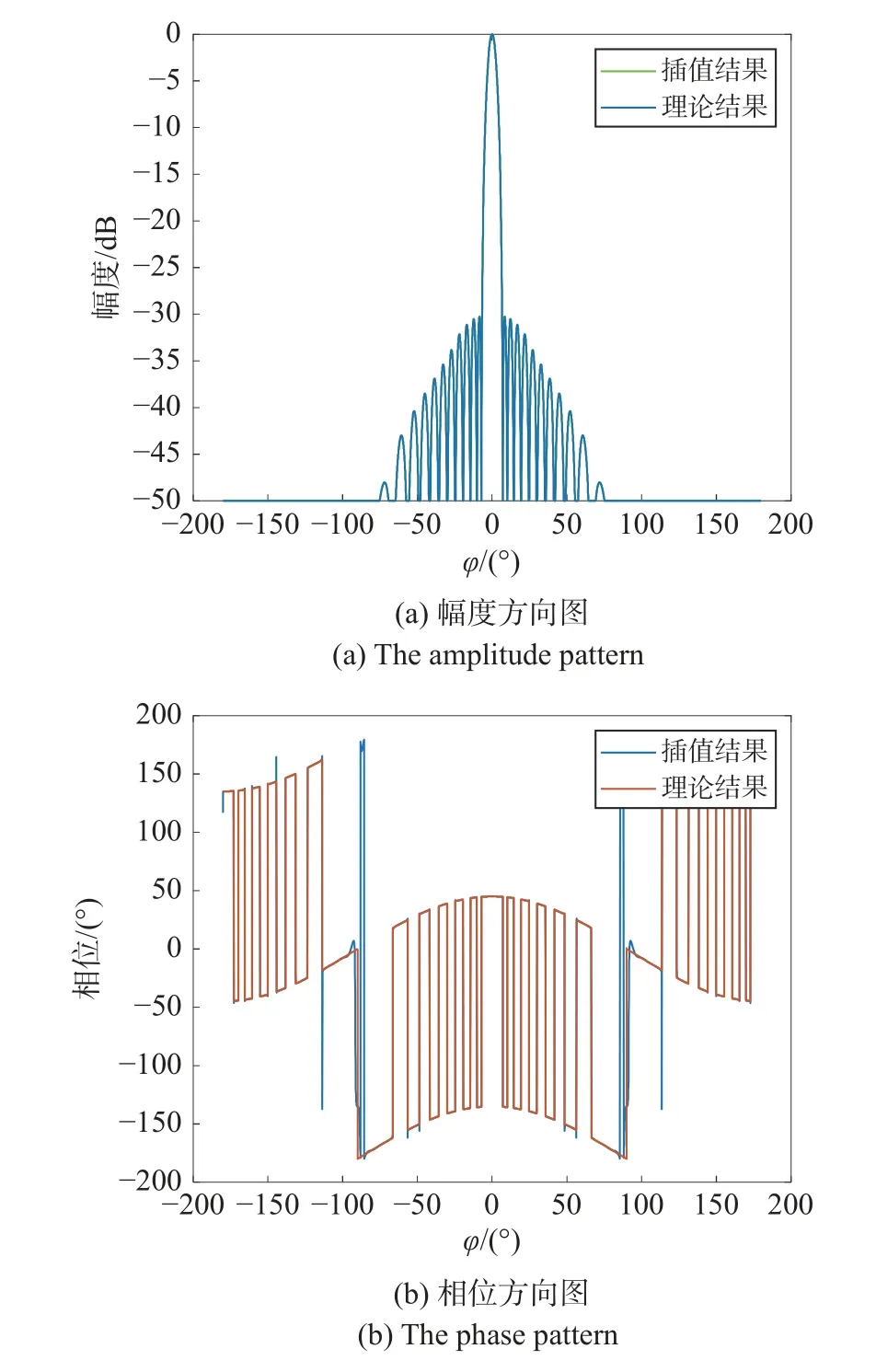
图3 插值后仿真方向图与理论方向图的比较Fig.3 The comparison between the pattern after interpolation and the theoretical pattern

从以上仿真结果可以看出，需要测试多任务时，例如对于200 个状态(状态数=通道数×波位数×频点数)波束宽度1°的天线进行远场或紧缩场测试，传统采样间隔为波束宽度的1/10，即0.1°，允许的最大采样速度约为0.1°/s，测试一次需60 min.应用本文方法，采样间隔为波束宽度量级，即1°，采样速度不变，因此测试一次为6 min，大大提高了测试效率.

2.2 实验验证

在微波暗室内对频率为12.225 GHz 的天线进行测量.天线旋转中心到天线最远点距离ρmin=43 mm，取N0=3，则N=14，J=2N+2=30，因此应用本文方法的采样间隔dφ=120/J=12°，待测天线3 dB 波束宽度为15.6°.可以看出，应用本文方法采样间隔接近天线3 dB波束宽度.

图4 为应用本文方法以12°采样间隔测得的幅度方向图和相位方向图.图5 为插值后方向图和以0.1°间隔实际测量的方向图比较，可以看出，插值后的方向图与实测方向图吻合很好.

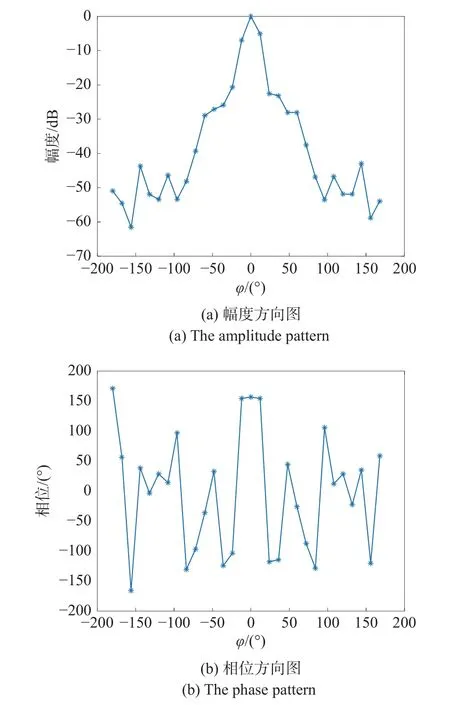
图4 插值前实测幅度和相位方向图Fig.4 The amplitude and phase patterns before interpolation

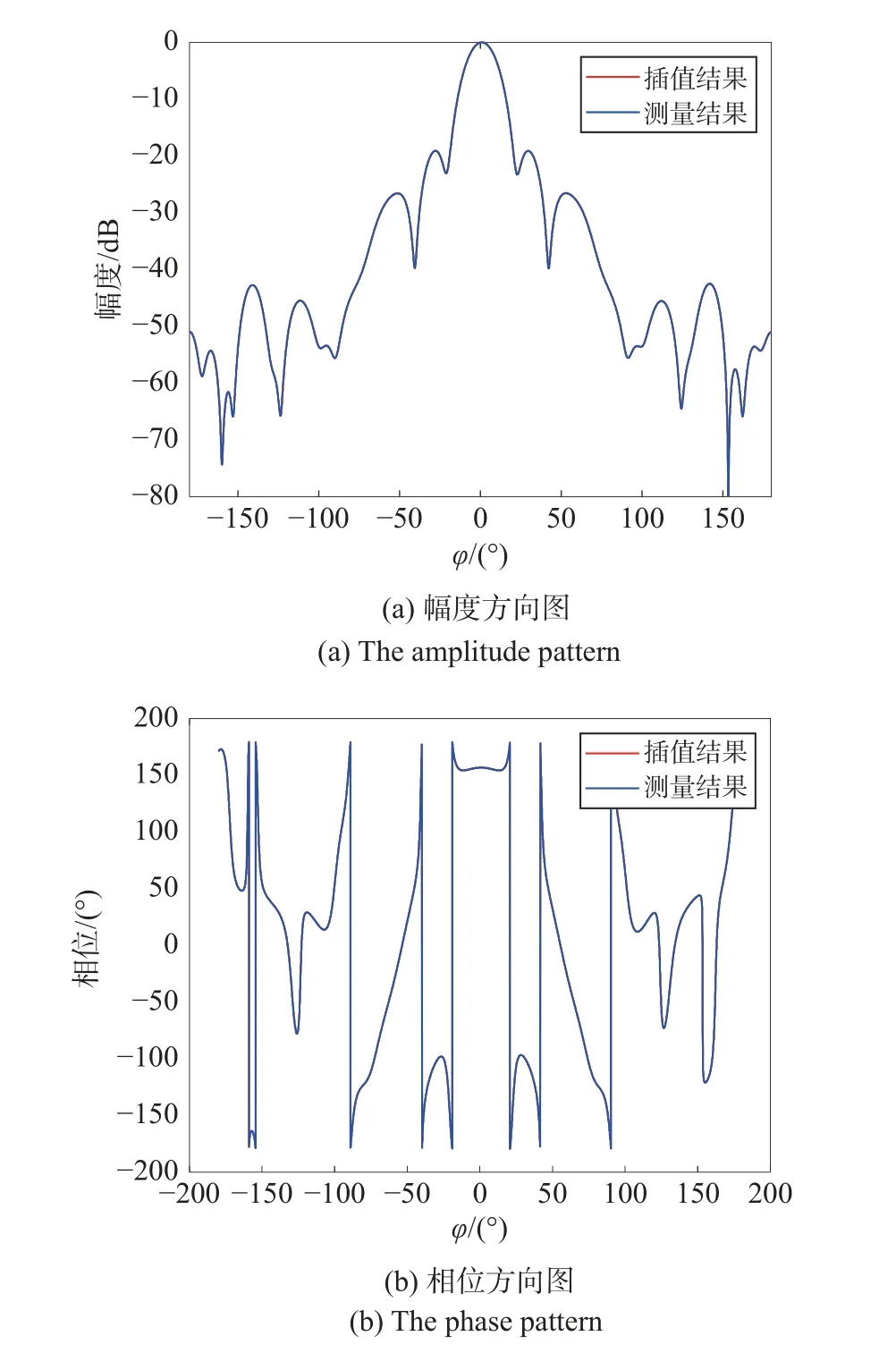
图5 插值后实测方向图与实测方向图的比较Fig.5 The comparison between the pattern after interpolation and the measured pattern

如果仅采用幅度信息插值，应用本文方法，采样间隔为6°，插值前方向图如图6(a)所示，插值后方向图和实测方向图如图6(b)所示，吻合度也很好.

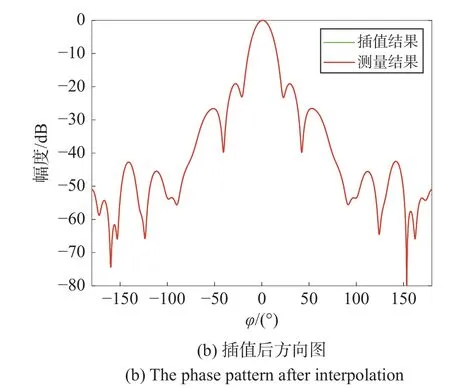
图6 仅用幅度信息插值得到的方向图与实测方向图的比较Fig.6 The comparison of the pattern after interpolation with amplitude information only and the measured pattern

综合仿真结果可以看出，应用本文提出的方法，采样间隔可以减小到天线3 dB 波束宽度量级；如果仅采用幅度信息插值，采样间隔为2 倍的3 dB 波束宽度量级，且恢复的幅度方向图和相位方向图与理论方向图吻合很好.

3 结 论

本文给出一种基于带限周期函数的Fourier 插值法，并将其应用在实际天线测量中，数值仿真结果和实测结果吻合较好，验证了此方法的正确性和有效性.本文天线分析模块应用于多通道、多波束、扫频测试中，可大大减少采样点数，从而显著提高测试效率，已成功应用于航天504 所天线远场测量系统中.