不均匀正应力下节段预制桥梁胶接缝的抗剪性能
2022-11-05张志浩张永平胡方健朱炯亦杜晓庆
张志浩 张永平 胡方健 朱炯亦 杜晓庆
1.上海大学力学与工程科学学院,上海 200444;2.上海市城市建设设计研究总院(集团)有限公司,上海 200125;3.上海工业化装配化市政工程技术研究中心,上海 200125
节段预制拼装桥梁具有工业化程度高、施工方便、质量易于控制、建造周期短等优点,近年来在我国得到了迅猛发展,在许多大桥的引桥部分和城市高架建设中均采用了节段预制拼装技术,如苏通大桥引桥、上海市沪闵路高架等。与普通混凝土桥梁相比,节段预制拼装桥梁的普通钢筋会在接缝处断开,预制节段通过后张预应力束联系在一起。因此,接缝的受力性能成为桥梁的薄弱部位。接缝通常可分为干接缝和胶接缝两种类型。干接缝在节段间无填充材料,施工速度快,但接缝处易渗水,对桥梁耐久性不利。胶接缝在节段间会填充环氧树脂,虽然增加了施工时间和成本,但环氧树脂可以起到防水作用。因此,胶接缝是工程中最常用的接缝类型。
国内外学者针对节段预制拼装桥梁的接缝剪切性能开展了大量研究。文献[1]对节段预制拼装桥梁的接缝进行了试验研究,研究发现在相同正应力下,胶接缝试件的承载力高于干接缝试件,胶接缝试件的破坏为脆性破坏。文献[2]通过对节段预制拼装桥梁接缝的试验研究发现:拼接缝试件的抗剪承载力随着正应力的增加而增加;接缝试件的抗剪承载力比相同条件的干接缝试件高20%~40%;单键齿干接缝的归一化剪切强度高于多键齿干接缝,AASHTO[3]规范抗剪承载力公式低估了单键齿干接缝的抗剪承载力而高估了多键齿干接缝。文献[4-5]根据文献[2]试验结果建立了键齿接缝试件的有限元模型,该模型计算值与试验结果吻合较好,并进一步采用校验的有限元模型进行键齿接缝试件参数分析。文献[6]在普通混凝土中添加钢纤维进行键齿接缝推出试验,发现添加钢纤维不能有效提高键齿接缝的抗剪承载力。文献[7]研究了胶接缝厚度对节段预制拼装桥梁受力性能的影响,发现过厚的胶层会降低桥梁整体刚度,增大预应力损失。文献[8]针对节段预制拼装梁桥的接缝开展了一系列试验研究,发现对于多键齿接缝试件,AASHTO[3]规范抗剪承载力公式应添加折减系数0.7。此外,文献[9-11]建立有限元模型对节段预制拼装桥梁的接缝抗剪性能试验进行模拟,并研究了环氧树脂胶的弹性模量、加载点的偏心距、键齿深度等参数对接缝抗剪性能的影响规律。文献[12-13]研究发现剪力键键齿配筋和布置体内束可以明显提高剪力键破坏时的延性,降低开裂荷载与极限荷载的比值,改变试件破坏形态。
综上所述,国内外学者已经采用试验和有限元分析对节段预制拼装桥梁接缝的抗剪性能做了较为全面的参数研究。但是,以往学者在研究正应力对节段预制桥梁接缝受力性能的影响时,大多采用沿高度方向均匀布置的正应力,而在实际工程中梁截面上的正应力分布在不同的工作阶段往往是不一致的。此外,实际工程中接缝处大多使用环氧树脂胶进行填充,而现有研究大多针对干接缝,关于胶接缝抗剪承载力的研究相对较少。因此,本文通过试验研究和有限元模拟结合的方式,深入研究不均匀正应力对节段预制拼装桥梁胶接缝抗剪性能的影响。
1 试验概况
1.1 试验设计
制作足尺键齿接缝试件,节段预制拼装桥梁接缝如图1所示。
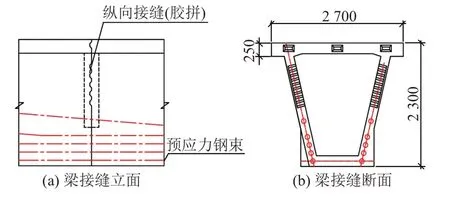
图1 节段梁接缝示意(单位:mm)
试件采用文献中较为常见的Z形,由阴齿、阳齿两个L形试件涂抹环氧树脂胶粘接而成,见图2。试件整体尺寸为1 170 mm(高)×600 mm(宽)×160 mm(厚)。键齿根部长120 mm,齿深40 mm,键齿倾角45°。此外,为了防止在试验过程中试件其他位置早于键齿区破坏,在试件内部搭建钢筋骨架,箍筋采用ϕ14的HRB400热轧带肋钢筋,其余钢筋均为ϕ22的HRB400热轧带肋钢筋,并在关键位置进行点焊。

图2 试件构造(单位:mm)
1.2 试验装置
试验加载装置由竖向力施加装置和水平力施加装置两部分组成。竖向力采用WAW-J2000电液伺服结构试验系统进行施加,该试验机最大负荷±2 000 kN。正应力施加装置由特制的钢约束箍和变频控制千斤顶组成。钢约束箍由2个钢反力支撑锚箱和4根高强度螺纹杆组合而成。首先用扳手将高强度螺杆的固定螺母拧紧,再通过变频控制千斤顶对接缝试件施加预加力,在试件两侧放置钢压板来控制加载区域,正应力通过钢压板均匀地传递至胶接缝粘接面。
为保证正应力大小恒定,在千斤顶的加载端部放置力传感器对水平力进行监控,保持试验过程中千斤顶施加的水平力大小不变。此外,为减少试件侧面和水平力施加装置之间的竖向摩擦力,在试件的两侧各布置2块厚20 mm的钢压板,在钢压板中间增设1块厚10 mm的聚四氟乙烯板,并在其正反面涂抹黄油。
试验采用非接触式的光学三维变形测量系统(Digital Image Correlation,DIC)辅助观测试验过程,通过连续拍摄试验过程中的试件照片,分析比较图像信息,进而获得试件的变形信息。试验时在试件剪切区域均匀随机喷涂斑点,将DIC设备架设于试件正面。通过该系统记录键齿剪切区域混凝土应变以及裂缝的开展情况。接缝处的竖向相对滑移通过线性位移传感器(Linear Variable Differential Transformer,LVDT)进行观测记录。试验加载装置见图3。

图3 试验加载装置
1.3 加载方案
通过千斤顶施加水平力,试件所受正应力为1 MPa;竖向力加载采用先力控制后位移控制的方案。第1阶段为荷载控制,采用分级加载,根据AASHTO[3]规范抗剪承载力计算公式预估各试件的极限承载力。加载时以50 kN为一级进行加载,达到每级目标荷载后静压1 min使试件充分受力,采集相关数据。当竖向力接近理论极限抗剪承载力时,进入第2阶段。将荷载控制更换为位移控制,设定位移加载目标值,加载速度为0.3 mm∕min,连续加载直至荷载降低到某一数值并开始稳定,此时荷载-位移曲线的下降段完成,平稳段出现。当LVDT所测剪切相对滑移达到5.0 mm时,试件彻底破坏,停止加载。
2 ABAQUS有限元模型
2.1 ABAQUS建模中的材料本构关系
2.1.1 混凝土本构模型
本文采用ABAQUS提供的混凝土塑性损伤(Concrete Damaged Plasticity,CDP)模型作为混凝土的本构模型进行建模计算。混凝土单轴受压的应力-应变关系式[14]为

式中:σc为混凝土压应力;η和k分别为关于应变和弹性模量的无量纲量;fcm为混凝土圆柱体抗压强度;Ecm为混凝土弹性模量;εc为混凝土压应变;εc1为峰值压应变。
对于混凝土破坏后的应力-应变关系,ABAQUS帮助文档[15]中指出:对于混凝土裂缝出现后的应变软化性能可以用拉伸硬化进行模拟。本文采用文献[16]提出的混凝土虚拟裂缝面上黏聚力与裂缝张开位移之间的关系来定义拉伸硬化,其表达式为
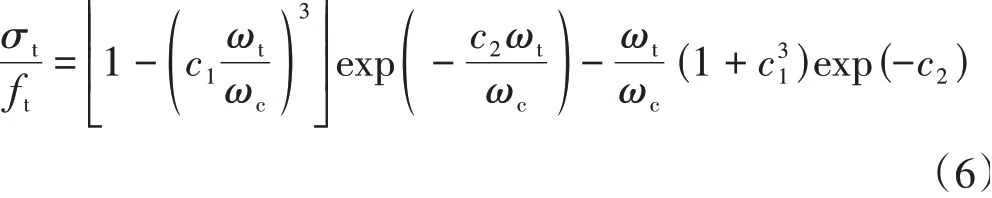
式中:σt为混凝土拉应力;ft为混凝土单轴抗拉强度;c1、c2为材料常数,分别取3和7;ωt为对应混凝土应力的裂缝口张开位移;ωc是应力为零时的裂缝口张开位移。
2.1.2 钢筋应力-应变关系
对于键齿接缝试件中钢筋的应力-应变关系采用双线性强化模型,即
当εs≤εy时

当εy<εs≤εu时
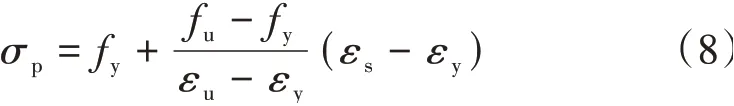
式中:σp为钢筋应力;Es为钢筋的弹性模量;εs为钢筋应变;fy为屈服强度;fu为极限抗拉强度;εy为屈服应变;εu为极限拉应变。
2.1.3 环氧树脂胶本构模型
试验采用的环氧树脂胶和混凝土界面的黏结强度为30 MPa,远大于混凝土的抗拉强度,表明键齿接缝试件的破坏位置并不是发生在环氧树脂胶和混凝土的黏结界面而是在混凝土上。此外,环氧树脂胶的抗压强度和抗拉强度远大于混凝土的抗压强度和抗拉强度,因此将环氧树脂胶简化为线弹性材料,其弹性模量为4 826 MPa,泊松比为0.2。
2.2 有限元模型设置
为充分还原试验过程,采用ABAQUS建立三维实体有限元模型,见图4。

图4 有限元模型设置
模型中混凝土和环氧树脂胶采用三维实体单元C3D8R,钢筋采用桁架单元T3D2。混凝土和环氧树脂胶之间的相互作用使用绑定约束(Tie)进行定义。试件与试验机平台之间的相互作用通过定义接触来模拟,接触属性采用罚函数摩擦模型和有限滑移假定,摩擦因数根据试验情况进行设置。
3 有限元模型验证
采用有限元模型对试件加载过程进行模拟,得到荷载-相对滑移曲线和裂缝开展模式,并与试验结果进行对比,见图5。其中裂缝图的左侧为有限元模拟结果,右侧为DIC观测所得试验结果。

图5 有限元模拟结果与试验结果对比
3.1 荷载-相对滑移曲线对比
试件加载过程可以分为4个阶段。
1)阶段Ⅰ。试件变形较小,施加荷载与相对滑移成线性关系。
2)阶段Ⅱ。试件发生塑性变形并开始出现裂缝,相对滑移不断增大,与有限元模拟所得荷载-相对滑移曲线相比,试件在裂缝出现以后刚度明显降低,在这一阶段到达极限承载力。
3)阶段Ⅲ。键齿上的裂缝迅速发展,同时相对滑移快速增长。与试验所得荷载-相对滑移曲线相比,有限元计算值突然下降,原因是有限元中混凝土材料一旦达到极限强度,就不再考虑其抗剪作用,模型中键齿全部发生剪切破坏而失效。
4)阶段Ⅳ。试件的荷载-相对滑移曲线到达平稳阶段,由于剪胀效应的影响,需手动调节保压千斤顶控制正应力保持在1 MPa,残余荷载在200 kN左右轻微波动。这部分抗剪承载力主要由骨料之间的咬合力和界面摩擦力来提供。
此外,试件的极限承载力有限元计算值为524 kN,比试验值(501 kN)高4.6%;相对滑移有限元计算值为0.738 mm,比试验值(0.887 mm)小16.8%,误差率均在20%以内。以上结果表明,有限元计算值与试验值总体吻合较好。
3.2 裂缝发展过程对比
为了在有限元模型中显示出开裂区域,将应变云图中的应变上限设定为混凝土极限拉应变,当混凝土单元拉应变超过极限拉应变时显示为灰色,灰度区表示裂缝的开展情况。结合图5可以看出,首先在上部两个键齿根部产生较大的剪切应变,随着施加的荷载不断增大,上部键齿根部出现裂缝。当施加荷载达到极限承载力时,底部键齿根部出现裂缝并向上发展,最终形成了主破坏面贯通整个剪切面。试件破坏形态为键齿根部的剪切破坏。
由以上结果可知,有限元模拟所得裂缝发展过程与试验情况吻合良好,有限元模型可以用来研究键齿接缝试件的裂缝发展情况。
4 不均匀正应力的影响性分析
不同阶段桥梁接缝位置截面正应力分布见图6。可知:在桥梁建成时,预制拼装混凝土桥梁在预加力和一期、二期恒载作用下,梁接缝断面上的应力沿高度呈均布状态;随着车辆、人群等荷载的增加,混凝土梁截面上下缘的应力大小相应地发生变化,呈梯形分布;当荷载继续增大,主梁截面下缘混凝土应力超过极限抗拉强度而开裂,裂缝向截面上缘延伸,梁体进入带裂缝工作阶段。这表明梁接缝截面上的正应力分布在不同的阶段是不一致的。因此,有必要进一步研究不均匀正应力对节段预制桥梁胶接缝抗剪性能的影响。

图6 不同阶段桥梁接缝位置截面正应力分布
4.1 不均匀正应力设置
在有限元模型中,对中间接缝剪切面施加正应力的方式和试验操作一致。在试件两侧施加正应力,通过混凝土传递至中间接缝剪切面。为使有限元模型中接缝剪切面上呈现出不同的正应力分布,需在试件侧立面上施加不同分布方式的正应力。建立3个有限元模型,控制剪切面等效正应力为1 MPa,即两侧施加的总水平力保持不变,但应力分布形态沿高度发生变化,其他参数保持一致,见图7。其中,M(0.5~1.5)表示侧立面下缘施加的正应力为0.5 MPa,侧立面上缘施加正应力为1.5 MPa,中间区域正应力呈线性分布,其他情况以此类推。
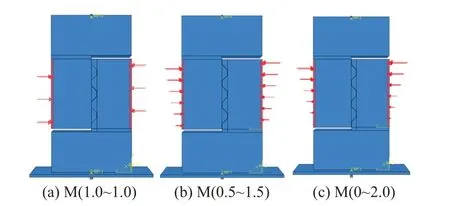
图7 正应力分布方式
接缝剪切面上的正应力见图8。可知:接缝剪切面上的正应力分布与图7中试件两侧施加的应力分布比较吻合。虽然在有限元模型中接缝面的顶部和底部附近存在应力集中,但该区域范围较小,对接缝剪切面上的正应力分布影响有限。

图8 接缝剪切面上的正应力
4.2 截面主拉应力分布对比
在3个模型上依次施加0、100、200、300、400 kN的竖向力,剪切面上的主拉应力分布见图9。
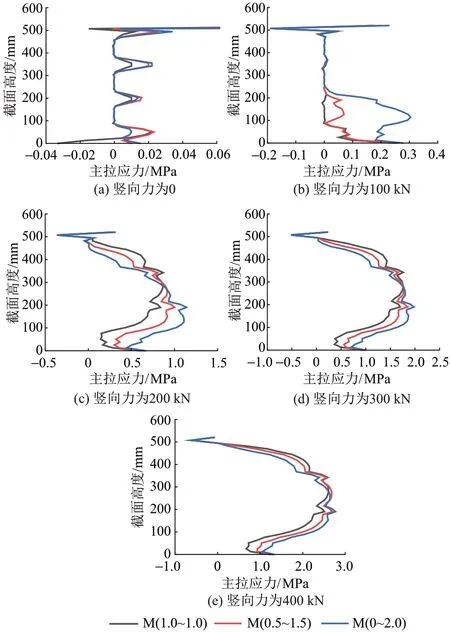
图9 不同模型剪切面上的主拉应力对比
由图9可知:
1)在剪切面上缘和下缘存在较强的应力集中。当竖向力为0时,3个模型剪切面上的主拉应力沿截面高度有较大差异;剪切面接缝平接段上的主拉应力均较高,而剪切面键齿根部的主拉应力为0。
2)当竖向力为100 kN时,模型M(1.0~1.0)剪切面的中部主拉应力基本为0;在剪切面的底部,模型M(0.5~1.5)的主拉应力大于模型M(1.0~1.0),模型M(0~2.0)变化则更明显。
3)随着竖向力的增大,3个模型主拉应力的大小、分布区域逐渐趋于一致,这是因为混凝土发生塑性变形以后,模型上的应力会重分布。因此,正应力分布不均匀会影响模型加载前期接缝剪切面上的应力状态,对于加载后期影响不大。
4.3 荷载-相对滑移曲线对比
模型M(1.0~1.0)、M(0.5~1.5)、M(0~2.0)的荷载-相对滑移曲线见图10。可知:3个模型的荷载-相对滑移曲线形态基本一致,均为先上升到达峰值承载力,然后快速下降到达残余承载力;3个模型的荷载-相对位移曲线的刚度基本一致。
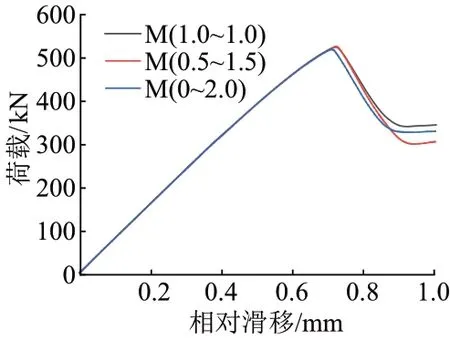
图10 不同试件的荷载-相对滑移曲线
此外,模型M(1.0~1.0)的极限承载力和破坏时的相对滑移分别为525 kN、0.722 mm;模型M(0.5~1.5)的极限承载力和破坏时的相对滑移分别为526 kN、0.723 mm,这两个模型的抗剪性能基本一致。而模型M(0~2.0)的极限承载力和破坏时的相对滑移分别为520 kN、0.710 mm,比模型M(1.0~1.0)的极限承载力和破坏时的相对滑移相比分别下降了1.0%、1.7%。
综上,在控制等效正应力大小相同的情况下,正应力不均匀分布对于键齿胶接缝模型的抗剪承载力影响不大。造成这种现象的主要原因有:三种不同应力分布方式作用下,等效正应力均为1 MPa,应力水平较低;混凝土塑性变形发生后,模型剪切区域应力重分布,模型剪切区域主拉应力的大小、分布逐渐趋于一致。
4.4 裂缝发展过程对比
不同正应力分布方式下,裂缝出现、裂缝发展到模型破坏的形态见图11。
对比图9和图11可知:
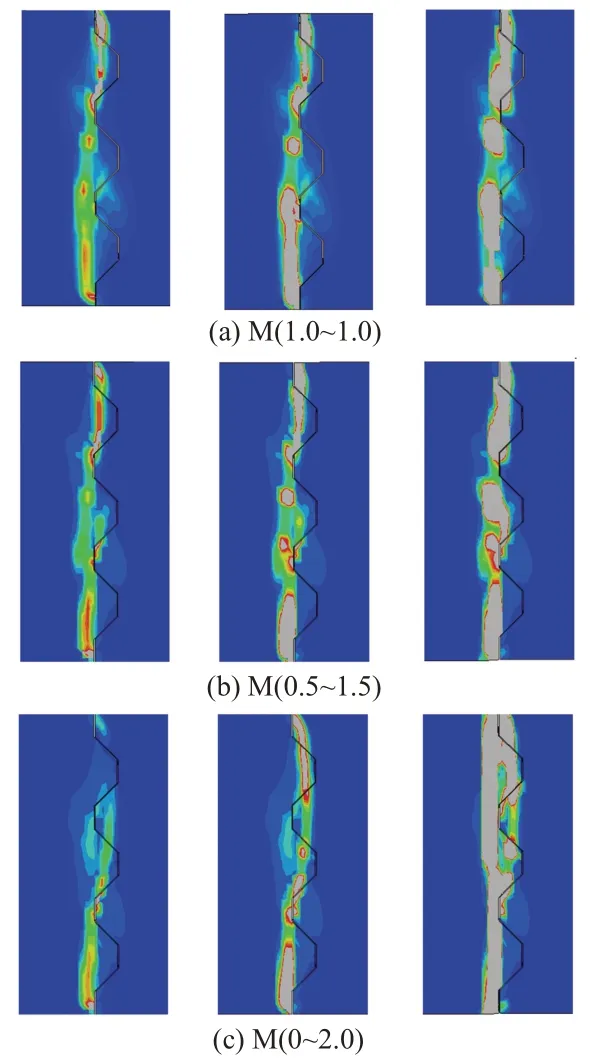
图11 不同应力分布方式下的裂缝开展过程
1)对于模型M(0~2.0),由于在键齿剪切区域底部施加的正应力水平较低,主拉应力增长较快,导致裂缝首先在底部键齿根部出现,然后裂缝随荷载增加而不断向上延伸,在此过程中阳齿域中部键齿和阴齿区上部键齿的前端被剪坏,最终阳齿区键齿根部的裂缝贯通。
2)模型M(1.0~1.0)和M(0.5~1.5)具有相似的裂缝发展模式,首先在键齿根部出现裂缝,然后随着荷载的增加裂缝不断拓展并最终贯通。
5 结论
1)有限元模拟所得试件的荷载-相对滑移曲线、裂缝开展模式与试验结果吻合良好,极限承载力和相对滑移的误差率均在20%以内。
2)正应力分布不均匀会影响模型加载前期接缝剪切面上的应力状态,施加正应力较小的位置主拉应力较大,并首先出现裂缝。
3)对于不同正应力分布的模型,随着荷载的增加,接缝剪切面上主拉应力的大小、分布区域趋于一致,这是因为混凝土材料产生塑性变形以后发生应力重分布。
4)在控制等效正应力大小为1 MPa的情况下,受剪切区域应力重分布的影响,截面应力分布不均匀对键齿胶接缝试件的抗剪承载力影响不大。后续研究中可采用提高等效应力水平或通过荷载试验方式进行更深入的探索。
