需求呈周期性变化的易腐品在线订购策略

刘珏夙

（广东工业大学 管理学院，广东 广州 510520）

0 引言

易腐品的特点是使用寿命短，在超过一定的时间后，这类商品就会失去部分甚至全部价值。这样的商品特点导致过多或过少的订购量都会使决策者损失一定的收益，因此订购量的合理确定具有重要的现实意义。报童问题是关于易腐品的库存订购决策问题。在传统报童问题的研究中，都假定需求的统计信息是可知的。而在现实的决策情景中，决策者往往难以准确掌握需求的分布情况。Scarf[1]首先提出了未知需求分布的决策方法，该方法在已知均值方差的情况下，给出了模型最优解。Gallego，等[2]在文献[1]的研究基础上进一步优化了订购规则，且考虑了更多的实际因素来扩展其分析。Chan，等[3]结合这一方法提出了一个配货优化模型，使得决策者能在不对任何一个产品的需求分布做具体假设的情况下，对订货种类和订货量进行联合优化。陈淮莉[4]研究了随机需求下多产品、多周期的生鲜品订购问题，从零售商的角度给出了最优订购量以及最优折扣。然而，这些研究仍然要求需求分布的均值和方差是可知的，并没有完全脱离统计假设。

在线算法仅依靠历史数据进行决策，而不需要再对未来的输入序列做出统计假设，能够用它来研究报童问题的在线订购策略。张桂清，等将在线算法引入到报童问题中进行了竞争比分析，在概率预期[5]和一般预期[6]两种情况下分别给出了风险算法。Abdel-Aal，等[7]在需求不确定的情况下结合市场选择理论，用鲁棒优化方法建立了选择性报童模型。2008年Kalnishkan，等[8]提出了一种基于专家意见的在线预测方法——弱集成算法（WAA）。该算法仅凭借历史信息对专家意见进行集成，并将集成结果用以决策。Levina，等[9]将弱集成算法应用于无统计假设的多期报童问题中，为报童提供了一个具体的在线订购策略。Zhang，等[10]进一步研究了非平稳环境的报童问题，采用策略切换的思想，将弱集成算法应用于动态专家意见，给出了具体的在线订购策略。在之后的研究中，Zhang，等[11]构建了针对两产品、多周期报童问题的在线订购策略，并证明了该策略具有理论保证。

在实际生活中，有相当一部分易腐品的需求会受到人类社会活动的影响，这使得我们在考虑易腐品需求变动时有迹可循。O’Neil，等[12]应用机器学习算法解决需求冲击下的无分布报童问题。王海燕，等[13]探讨了需求分布规律变化情况下的报童订购决策问题。此外，有一些易腐品的需求会随着节假日和季节交替呈现出显著的周期性特征，例如电影票的订票需求。由于大多数人的闲暇时间都集中在非工作日（如周末或者节假日），因此电影院的观影人数往往是非工作日多、工作日少，从而导致电影票的非工作日需求高、工作日需求低；与这一情况相反的是写字楼和学校周边的餐饮店，这类餐饮店受到主要消费人群的活动规律影响，其需求规律通常表现为工作日高需求，而非工作日低需求。在上述两个例子中，需求都以某一固定的时间段为变动周期，在每一个变动周期内，需求表现出低-高或高-低的交替变化。将这类需求称作周期性变动需求，本文以低-高需求为例研究了需求周期性变动下多阶段报童问题的在线订购决策方法。在需求的周期性变动规律可获取前提下，本文应用WAA算法，基于历史需求数据给出了具体的订购策略，并理论分析策略的竞争性能。

1 基于弱集成算法的在线订购策略

弱集成算法[9]根据专家的历史表现来调整其权重，以提高在线决策者的竞争性能。给定各个专家的初始权重，在每一个决策期对专家的收益进行重新计算，并根据计算结果更新专家在下一决策期的权重。沿用以往研究中的记号，表1给出了主要记号及其含义。

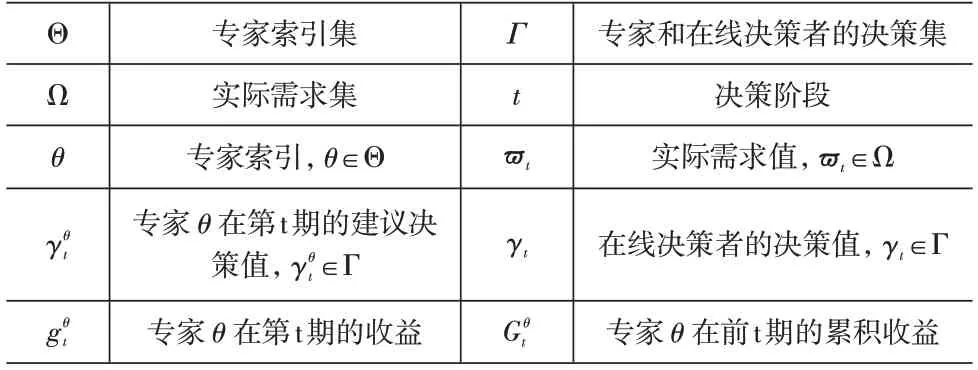
表1 WAA使用的主要记号及其含义

在每个决策期t=1,2,...,T，专家的标准化权重由式（1）给出。

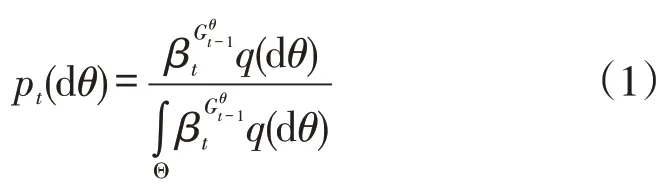
算法1弱集成算法（WAA）输入：实际决策值ϖ1,ϖ2,...,ϖT；输出：最终累积收益GT。(0)在线决策者和专家决策体的初始收益皆为0，即G0=0，Gθ 0=0；(1)在每个决策期t=1,2,...,T进行步骤（2）-（7）循环计算；(2)计算各专家的标准化权重；(3)专家决策体给出专家预测意见γθ t；(4)在线决策者在集成专家意见后做出预测：γt=∫Θ γθ t pt(dθ)；(5)得到实际决策者的结果ωt；(6)计算在线决策者和各专家的收益gt，gθ t；(7)更新在线决策者和专家的累计收益Gt，Gθ t；(8)重复步骤(2)-(7)，直至所有决策期结束。

当决策总周期数为T时，引理1给出了弱集成算法实现的累积收益下界。

引理1当收益函数g的界为-L≤g≤0（L为一个固定常数）时，对于任意的期数T，WAA的累积收益均满足：

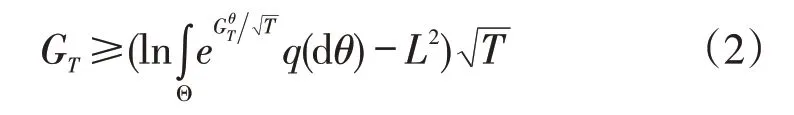
在需求呈周期性变动的多阶段报童问题中，假定报童在每一期的期初决定当期订购量，且此时当期的实际需求量尚不可知。在报童确定订购量后，实际需求也随之获得。对报纸这类易腐品而言，一旦报童确定当期订购量，在这一期中途不能进行补订，在这一期结束后，订购的剩余量也不具备回收价值。

以一个特定的时间段ρ作为规律性变动的最小周期，根据需求特征的不同，进一步将每个变动周期划分为不同的部分。以低-高交替变化的周期性需求为例，每一个变动周期中均包含低需求期和高需求期。用d表示低需求期时的实际需求量，d′表示高需求期的实际需求量，x和y分别表示在低需求期和高需求期中报童对产品的订购量，x和y分别通过集成专家意见获得。用Θ(Θ=Θ1⋃Θ2)表示专家池，其中低需求期专家池Θ1的专家索引为θ，高需求期专家池Θ2的专家索引为θ′。第t期的产品具体需求量无法确定，但可知在低需求期时，产品的需求量d和报童的订购量x为区间[B1,B1′]中的任意实数，在高需求期时，产品的需求量d′和报童的订购量y为区间[B2,B2′]中的任意实数，且有B1′≤B2。

设每一天为一个决策期，T为总的决策天数。为方便论述，设在前T天中共包含N个完整的需求变动周期，其中N∈ℤ。在每个需求变动周期中，包含ρ个决策天数，且有ρ=μ+ν。其中，μ表示一个周期内包含的低需求天数，ν表示一个周期内包含的高需求天数，在周期性变化的需求中，ρ、μ和ν均为确定的常数。将低需求期构成的决策天数总和记为T1，将高需求期构成的决策天数总和记为T2，则有T=T1+T2。从初始决策期开始，需求做低-高交替变化，记：

即有A=A1⋃A2。对于任何的t∈A，设需求为dt。当t=nρ+i,i=1,2,...,μ时，t∈A1，且 有t1=nρ+i-nν，则此时专家意见集为Θ1。当Θ1中的专家θ的订购量为时，该专家在第t期的收益为：

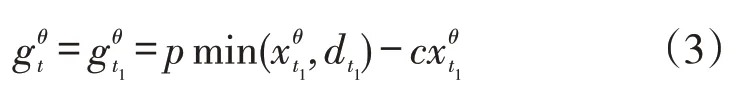
在前t1个低需求期的累积收益为因此，报童在第t期的订购量为xt1时，其收益为：

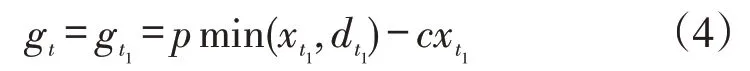
在前t1个低需求期的累积收益为

类似地，当t=nρ-j，j=ν-1,...,0时，t∈A2，且有t2=nρ-i-nμ，则此时专家意见集为Θ2。当Θ2中的专家θ′的订购量为时，该专家在第t期的收益为：

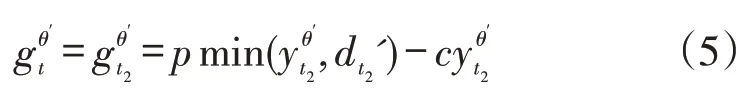
在前t2个高需求期的累积收益为因此，报童在第t期的订购量为yt2时，其收益为：gt=gt2′=pmin(yt2,dt2′)-cyt2；在前t2个高需求期的累积收益为

定理1在收益函数式（4）和式（5）的基础上，应用弱集成算法对静态专家意见进行集成，可得到需求呈低-高周期性变化报童问题的在线订购策略。

证明：考虑到低需求期和高需求期的需求差异，对低需求期和高需求期分别设置对应专家池，每个专家在任何一期总是推荐一个固定订购量，每一期选择对应的专家池中的静态专家意见进行集成，在选择专家池前，需要先判断当前决策期处于周期中的低需求期还是高需求期。根据弱集成算法的决策流程，可知当第t期为低需求期(t∈A1)，且对应低需求期序列的第t1期时，报童的订购量为：

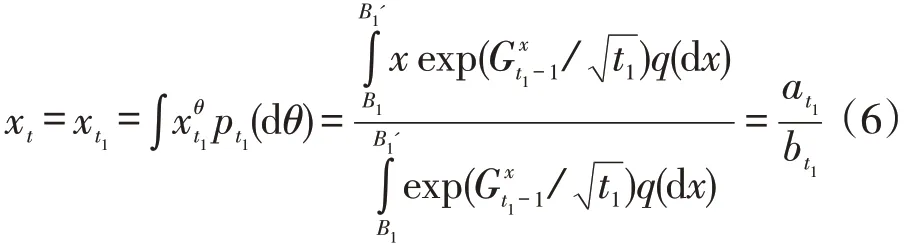
当第t期为高需求期( t∈A2)，且对应高需求期序列的第t2期时，报童的订购量为：

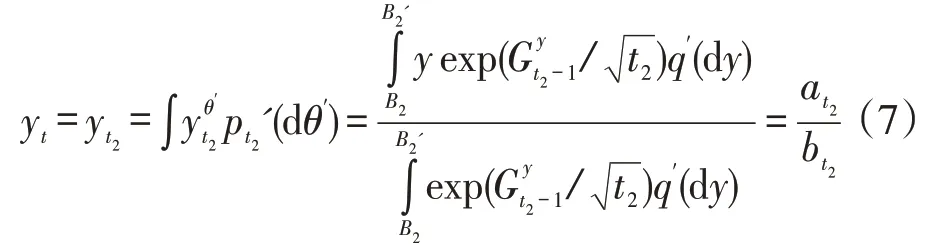
当q(dx)和q′(dy)分别为[B1,B1′]和[B2,B2′]上的均匀分布时，采用Levina，等[9]给出的求解方法。若第t期为低需求期，则第t期时可获得前t1-1个低需求期的历史需求序列d1,d2,...,dt1-1，令其顺序统计量为d(1),d(2),...,d(t1-1)，且d(0)=B1，d(t1)=B1′。

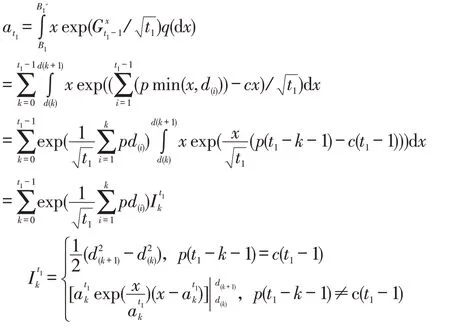
同理可得：

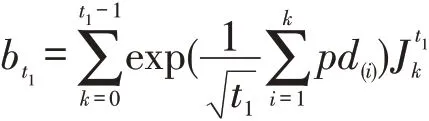
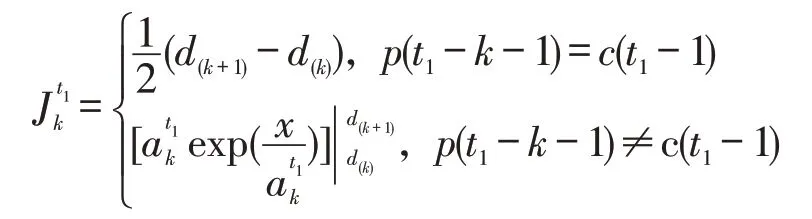
采用类似的方法，若第t期为高需求期，则在第t期时可知前t2-1个高需求期的历史需求序列。令其顺序统计量为且。令k′=1,2,...,t2-1。可得：

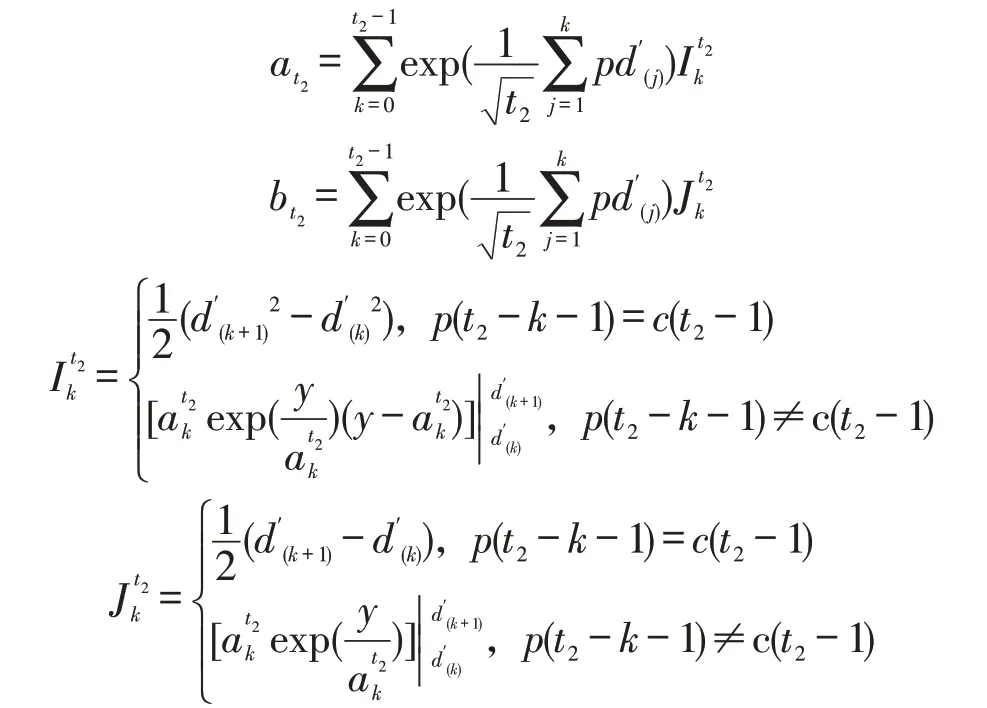
综上，针对需求呈低-高周期性变化的报童问题，本文给出了具体的在线订购策略，即若第t期为低需求期，订购量为xt=at1/bt1，若第t期为高需求期，订购量为yt=at2/bt2，并将此策略记为ASP。

2 在线订购策略的竞争性能分析

对于定理1给出的在线订购策略ASP，应用引理1，定理2给出了以最优专家策略的累积收益为基准时该策略竞争性能的理论保证。

定理2对于需求低-高周期性变动的多阶段报童模型，按照在线策略ASP进行决策时，报童的累积收益满足：

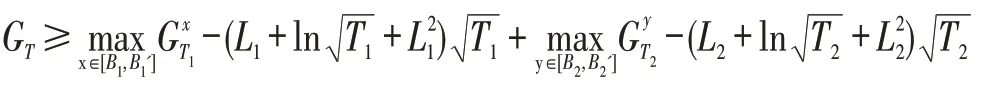
其中，Li=(Bi′-Bi)p，i=1,2，Λ=max(p-c,c)。

证明：由收益函数的定义式可知，对于低需求期而言，订购量等于需求量且为最大值B1′时，收益达到最大值；当实际需求为最小值B1而报童的订购量为最大值B1′时，收益取到最小值，即有：

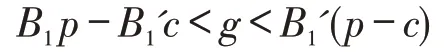
不失一般性，令g=g-B1′(p-c)，则有：

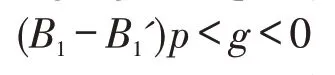
因此，在应用引理1分析在线策略的竞争性能时可知：

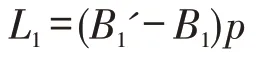
考虑任意两个专家策略的累积收益差值，若有两个专家的固定订购量分别为θ1和θ2，由前面的分析可知，经过T1期后，这两个专家实现的累积收益和满足关系式：

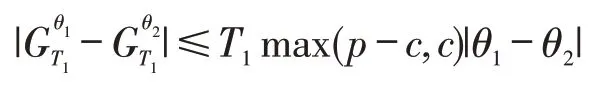
令Λ=max(p-c,c)，则根据引理1和文献[9]的方法，有：

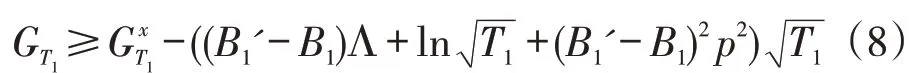
同理，对于高需求期而言，有：

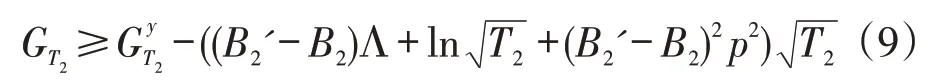
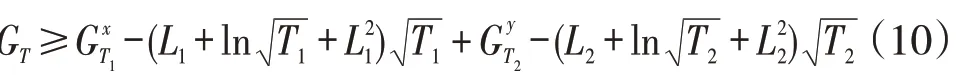
由式（10）可知，随着总决策天数T的增大，在线策略的平均累积收益逐渐接近低需求期固定订购量x和高需求期固定订购量y的平均累积收益。由于x和y是任意的，因此它们分别可以是使得累积收益和达到最优的固定订购量策略。事实上，当T→∞时，易得：

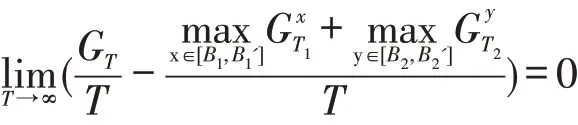
当需求不呈现周期性变动，即B1′=B2′=B，B1=B2=0，T1=T，T2=0时，有L2=L1=Bp，式（10）变成式（3），该结果退化成Levina，等[9]的研究结果，因此本文是文献[9]的推广研究。

3 数值算例分析

本节运用数值算例进一步验证策略ASP的竞争性能，记ASP对应的最优专家策略为BASP。为方便对比分析，将Levina，等在文献[9]中构建的策略记为AS，对应的最优专家策略记为BAS。在计算订购量时，先判断第t期属于哪一种需求期，再根据判断结果来选择式（6）或（7）进行计算，即可得出相应的订购量xt或yt。为了便于计算，对需求量和报童的订购量进行整数化处理，即有：

根据需求周期的变化规律，依次在[0，50]和[50，100]间随机生成90个随机整数，作为前90天的实际需求序列。随机产出10组不同的随机需求序列进行试验，表2给出了每次试验中在线策略ASP与其对应的最优专家策略BASP的累积收益比较，其中RAT表示ASP与BASP实现的累积收益比值。从表2中的30次试验结果来看，ASP与BASP的比值都大于0.94，且在第7次的试验下得到了最大值0.970 675，由此可见，ASP具有较强的竞争性能。

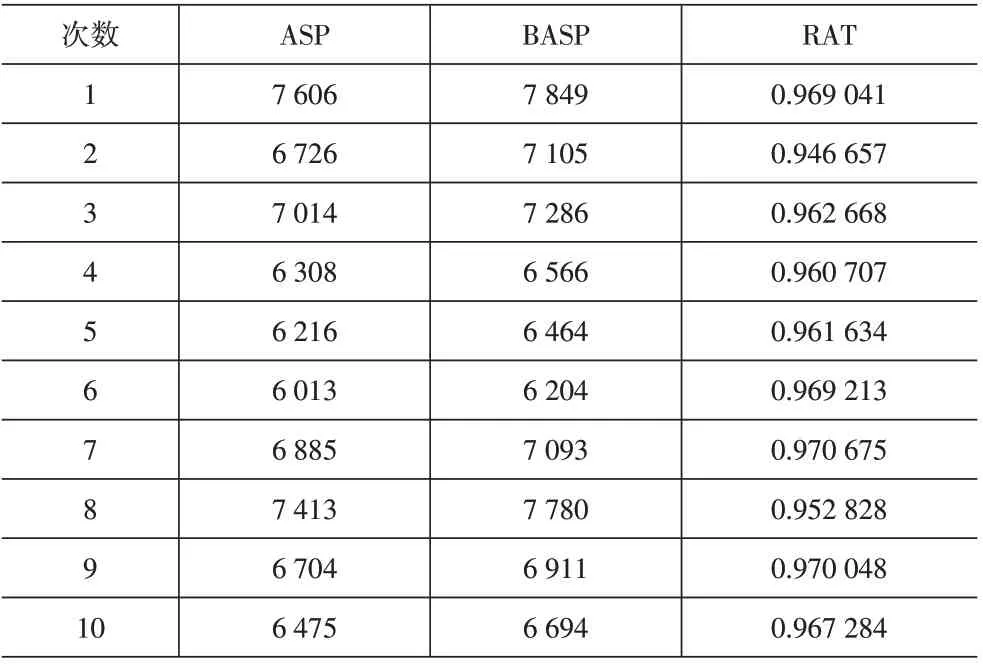
表2 不同随机需求下ASP与BASP的累积收益

为了观察ASP对AS的改进效果，以第1次试验中所用的需求序列为例，比较ASP和AS的日累积收益，结果如图1所示，其中叉号符表示ASP的日累积收益，圆圈表示AS的日累积收益。由图1可知，ASP和AS在前90天的日累积收益分别为7 606和4 012。ASP的累积收益明显大于AS的累积收益，说明在原有算法的基础上考虑需求的周期波动能提高决策者的收益。

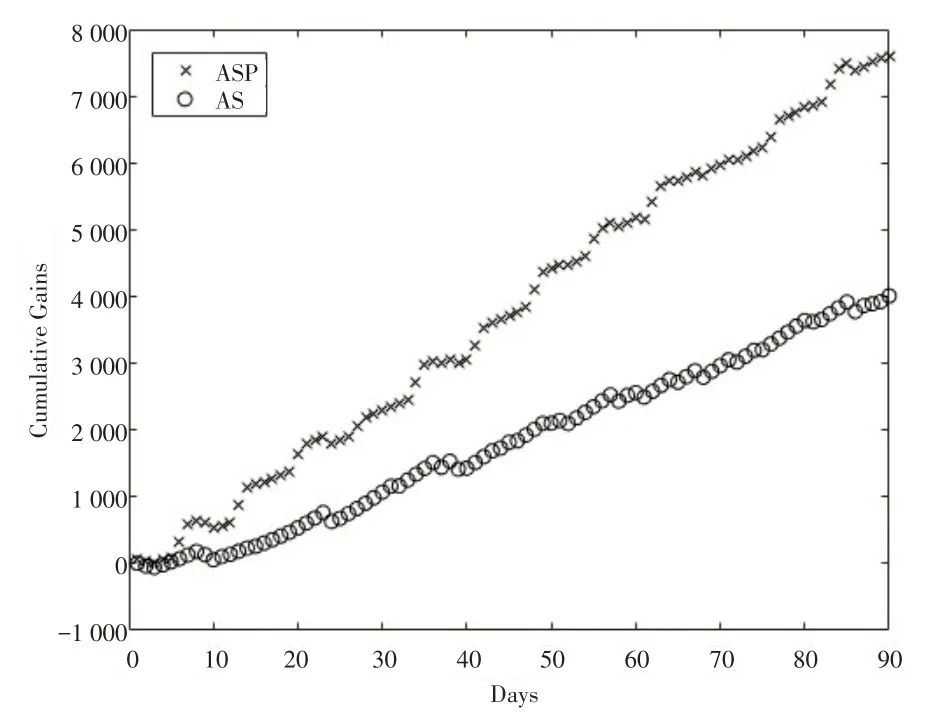
图1 ASP与AS的日累积收益比较

第一次试验中ASP和BASP的日累积收益比较如图2所示。由图2可知，本次试验中ASP和BASP的前90天的日累积收益分别达到7 606和7 849，二者的日累积收益非常接近，进一步证明了该策略相对于基准策略最优专家策略具有较强的竞争性能。

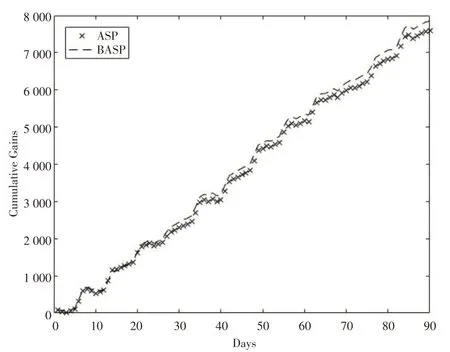
图2 ASP与BASP的日累积收益比较

当历史数据越充分时，ASP决策的结果就会越接近固定的最优专家的决策方案。调整决策的期数，计算ASP和BASP的累积收益，结果见表3。由表3可知，ASP的竞争性能会随着决策期数的增加而增强，当决策天数为600时，竞争比已经大于0.99，此时ASP的累积收益已经基本等于最优专家的累积收益。

表3 不同决策周期下ASP与BASP的累积收益

4 结语

本文在传统报童问题的基础上，结合现实因素，研究了需求呈周期性变动情形下的订购决策方法。采用集成专家意见的弱集成算法对固定的专家意见进行集成，给出了具体的在线订购策略。从理论上对该在线策略的竞争性能进行了证明，用数值算例进一步说明了策略能追踪到最优专家策略且获得与最优专家策略相当接近的累积收益，并对参数的敏感性进行了分析。这为与报纸具有相似特征的易逝品库存控制问题提供了一定的管理启示：首先，在考虑需求周期变动的情况下，为易逝品零售商的订购决策提供了参考，有利于零售商快速有效地通过历史信息进行订购决策，在满足市场需求的同时充分发挥现有资源的作用以达到自身收益的最大化；其次，对于易逝品的零售商而言，该在线决策方法可作为他们在长期持续决策中调整订购计划的根据，并能保证零售商在长期决策中可获取到具有竞争性的收益。本文研究周期性变动需求情形下的多阶段报童在线决策问题，其中用于学习参照的专家意见是静态的。但是，在面对复杂多变的市场环境时，专家的意见也会随着市场披露信息的变动而调整其推荐订购量。因此，考虑到在多阶段报童中专家意见可以依据专家自身对市场信息的敏感程度动态地调整，如何学习动态的专家意见并为零售商在市场中制定出更优的订购决策是需要进一步思考和研究的问题。