基于强制环状流工况的湿气测量数值模拟研究*
2022-11-05雷玲卷张兴凯廖锐全王智慧郑炜标时国伟
雷玲卷 张兴凯 廖锐全 王智慧 郑炜标 时国伟 刘 明
(1.长江大学石油工程学院 2.中国石油天然气集团公司气举试验基地多相流研究室3.油气钻采工程湖北省重点实验室 4.青海中油甘河工业园区燃气有限公司 5.西安交通大学动力工程多相流国家重点实验室 6.中国石油化工有限公司胜利油田分公司石油工程技术研究院)
0 引 言
湿气广泛存在于石油和天然气开采和运输过程中。 从油气田开采出来没有经过处理的天然气,因为携带少量水或轻质烃类,通常称之为湿气。目前,国际上通用把Lockhart Martinelli数XLM≤0.3的天然气与液相的混合物定义为湿气[1]。由于操作压力、温度、流速以及液相含量的影响,相比单相流动,湿气流态异常复杂,所以湿气测量的难度也大大增加。湿气计量主要分为分离计量法和在线不分离计量法。分离计量法生产工艺流程复杂、设备庞大、成本高且效率偏低;在线不分离计量法不仅降低油气田的投资和运行成本,还提高了其生产效率和科学管理水平。在线不分离湿气计量技术日渐成熟,取代分离计量正在稳步进行中。
差压式流量计在湿气计量中应用非常广泛,如孔板流量计、文丘里流量计、内锥流量计等。然而从现有湿气流量计测试情况来看,湿天然气通过差压式流量计时,由于液相的存在,其压差会比等量的气相单独流过时偏高,这种现象被称为“虚高”。显然,为了得到真实的气液流量,液相的存在所产生的测量差值需要修正模型进行修正。为此,国内外学者先后针对不同的差压式仪表提出了大量的虚高修正模型,其中比较有影响力的有Murdock模型[2]、林宗虎模型[3]、Chisholm模型[4]、De Leeuw模型[5]以及Steven模型[6]等。Murdock模型只涉及到XLM对虚高的影响;Chisholm模型的修正系数涉及气液密度比值,考虑了工况压力及XLM对虚高的影响;De Leeuw模型修正系数考虑了工况压力及气相弗劳德数Frg的影响。因为这些修正模型仅考虑了虚高的部分影响因素,是基于不同的差压元件在不同的测试条件下导出的经验关系[7],且通常是在XLM已知的情况下建立的,然而实际生产过程中XLM都未知。2020年孟宇飞等[8]研究了一种基于强制环状流的湿气双参数测量方法,能够较为准确地测量XLM,但是该测量方法是在常温常压条件下得到的,其通用性相对较差。
数值仿真试验不仅可以有效缩短研究时间,而且可以减少实流试验相关成本。近几年来,计算流体力学(CFD)方法在多相流计量方面应用广泛。国内外学者对差压式流量计的仿真研究和应用表明,只要网格质量好,且选择合适的计算模型和仿真方法,差压式流量计的数值模拟试验可达到较好的效果[9-10]。
2012年徐英等[11]基于数值模拟试验提出一种高压条件下文丘里湿气虚高的预测方法,与英国国家工程实验室高压实流试验数据进行比较,其虚高预测值的最大相对误差为5.14%,平均相对误差小于2.8%;同年,HE D.H.等[12]利用离散相模型(DPM)研究了文丘里管内多相流流动特性。他们指出,与单相气体相比,多相流在喉部区域压力显著下降,且随着液相含量越大,喉部压力下降得越快。2013年K.PERUMAL等[13]利用CFD方法,模拟了高压下湿气可压缩湿气流动,研究了文丘里管的几何规格对湿气虚高预测模型的影响,结果表明,虚高值随着直径比的增大而减小,而收缩角对虚高值无影响。2019年JING J.Q.等[14]利用CFD方法,研究了高压条件下,文丘里管中湿气的流动特性以及虚高模型的适用性,结果表明,虚高随XLM和气体体积流量的增加而增加,随压力的增大而减小。2020年闫嘉钰等[15]利用水平文丘里管结合伽马射线技术,提出了新的高压湿气虚高修正计算模型。2021年邓荣等[16]采用Eulerian多相流模型,研究了双文丘里多相流量计内气液两相流流动特性,分析了各因素对双文丘里管的压力和压差的影响。由以上文献调研可知,数值模拟方法在研究湿气通过文丘里管时具有较好的可行性。
本文利用数值模拟方法,以甲烷-水为介质,对由旋流器和文丘里管组成的湿气测量装置实际气井生产条件下湿气虚高特性进行了研究,建立了基于强制环状流压差特性的文丘里管湿气测量修正模型。
1 测量装置和测量原理
1.1 数值模拟测量装置
本文基于文献[8]的测量装置(见图1)进行实际气井工况下湿气虚高特性的数值模拟。由于孟宇飞等是在常温常压条件下提出的湿气双参数测量模型,其在实际操作条件下的适用性尚未得到验证,且实际生产中,湿气计量工况(压力、温度等)变化相对较大,所以应根据具体的使用工况对其准确度进行分析和判断。
由此,本文重点对实际气井工况下,由旋流器和文丘里管组成的湿气测量装置进行数值模拟。该装置共设置3个取压点,分别为旋流器之后中心压力点pC、管壁压力点pA和喉部管壁压力点pB,其中pA和pC位于同一横截面上,通过获得文丘里管喷嘴节流压差Δpa和离心压差Δpr来进行湿气测量,其中Δpr和Δpa分别由公式(1)和式(2)计算。
Δpr=pA-pC
(1)
Δpa=pA-pB
(2)
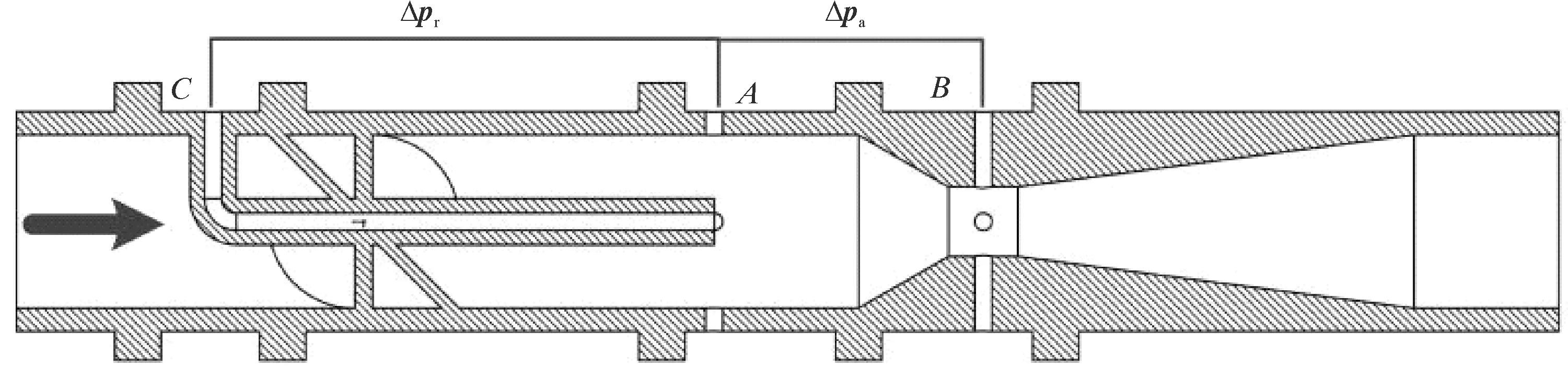
图1 湿气测量装置的几何结构Fig.1 Geometric structure of wet gas measurement device
1.2 湿气测量原理
湿气流过文丘里管的质量流量可表示为:
(3)
文丘里管测量湿气时,气体虚高修正系数Φg可表示为:
(4)
式中:Wtp为湿气质量流量,kg/s;Δpa,tp为湿气压差,Pa;Δpa,g为气体单独流过文丘里管的压差,Pa;Wg为实际气体质量流量,kg/s;Φg为虚高修正系数;C为流出系数;ε为流体可膨胀系数;β为节流比;d为喉部直径,m;ρg为流体密度,kg/m3。
理论与试验研究表明:虚高修正系数Φg与L-M参数XLM、气相弗劳德数Frg、压力p、温度T以及气液密度比等密切相关[11],因此, 虚高修正系数Φg可以表示为XLM、Frg、p、T以及气液密度比ρl/ρg的函数:
(5)
其中:
(6)
(7)
(8)
(9)
式中:XLM为Lockhart-Martinelli数,简称为L-M数;g为重力加速度,m/s2;wl和wg分别为液相和气相的质量流量,kg/s;φB为液相的体积含量;Q1为液相体积流量,m3/s;Qg为气相体积流量,m3/s;ρl和ρg分别为液相和气相的工况密度,kg/m3;Frg为气相弗劳德数;usg为气相表观流速,m/s;D为入口直径,m。
由虚高修正系数的函数关系式(5)知,只有当L-M数XLM、气相弗劳德数Frg、压力p、温度T以及气液密度比ρl/ρg都已知的情况下才能得到Φg。实际生产中,压力和温度都可以通过测量仪表得到,但是XLM、Frg都比较难获取,即使通过其他方法获得这2个参数,也会存在一定的误差。因此本文引入了无量纲参数K。K为Δpa和Δpr的比值,Δpr的主要影响因素为离心力,离心力与湿气的密度以及流量密切相关;Δpa的主要影响因素为湿气的摩阻压降和加速压降,而这2种压降主要取决于湿气黏度、流量等因素。因此,K其实是一个反映湿气流量、混合密度和混合黏度的参数。将虚高修正系数Φg和液气的质量流量比wl/wg转化为比值K、温度T、压力p和Frg的函数,计算公式如下:
(10)
Φg=fa(K,p,T,Frg)
(11)
(12)
2 数值模拟方法
2.1 几何建模和网格划分
图2为测量装置的几何模型。图3为出口网格示意图。模型结构和网格划分的质量直接影响到数值模拟的可行性、收敛性和计算精度。本文采用ANSYS Workbench中提供的ANSYS Meshing应用程序进行网格划分。由于文丘里喷嘴前安装了结构较为复杂的叶片式旋流器,为保证模拟的准确性和效率,所以采用结构化和非结构化的混合网格,并进行网格独立性验证。网格独立性根据节流压差的变化来验证,如图4所示。随着网格数的增加,节流压差先增大后基本不变,当网格数大于1 250 000时,节流压差基本不变,所以最终确定最优网格数是1 250 000个。

图2 测量装置几何模型Fig.2 Geometric model of measuring device

图3 出口网格示意图Fig.3 Schematic diagram of outlet grid

图4 网格无关性验证Fig.4 Grid independence verification
2.2 计算模型和控制方程
用Fluent19.0软件进行数值模拟。由于文丘里管内涉及气液混合物的压力变化,所以多相流模型选择欧拉(Eulerian)模型,该模型可以计算有不同体积分数的混合物中单相的速度、温度和密度[17]。雷诺应力模型(RSM)中考虑了旋流效应。RSM模型更适合叶片式旋流器的数值模拟[18],因此本文湍流模型选择RSM模型。文丘里管内的控制方程为连续性方程、能量守恒方程和动量守恒方程[19]。
连续性方程:
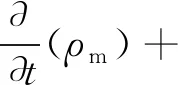
(13)
(15)
式中:ρm为混合相密度,kg/m3;t为时间,s;vm为混合相质量加权平均速度,m/s;n为相;αk、ρk和vk分别为第k相的体积分数、密度和速度。
动量守恒方程:
(16)
(17)
能量守恒方程:
(18)
式中:ρ为液体密度,kg/m3;δij为kronecker系数;cp为比热容,J/(kg·K);T为温度,k;τij为应力张量;gi和Fi分别为i方向上的重力体积力和外部体积力,N/m3;ui、uj分别为i方向和j方向的速度分量,m/s;u为速度,m/s;μ为运动黏度,Pa·s;k为流体传热系数,W/(m2·K);p为静压,Pa;ST为流体的内热源及由于黏性作用流体机械能转换为热能的部分,J,简称为黏性耗散项。
2.3 边界条件
边界条件采用速度入口和压力出口,其他物性参数根据相应温度和压力设定。对实际工况下的湿气进行仿真预测,仿真介质气相为甲烷,液相为水。气相和液相分别根据压力和温度的不同而设定相应的密度和黏度等参数。数值模拟方案具体如表1和表2所示。
保持XLM、压力p和节流比等参数不变,研究温度变化对压差虚高的影响;保持XLM、温度及节流比等参数不变,研究压力变化对虚高的影响;保持气相弗劳德数、压力、温度及节流比等参数不变,研究XLM对压差虚高的影响。

表1 同一气相流量, 4个压力下不同温度的模拟方案Table 1 Simulation scheme at constant gas flow rate,4 pressures and different temperatures
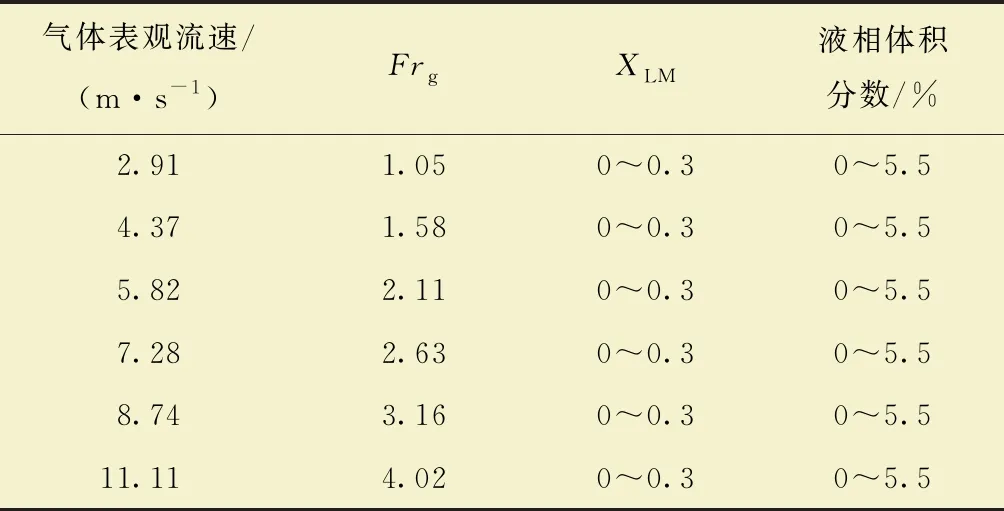
表2 压力6 MPa,温度60 ℃的仿真方案Table 2 Simulation scheme at 6 MPa and 60 ℃
3 仿真试验结果分析
3.1 气液相分布规律
以p=6 MPa,T=60 ℃,Frg=2.63工况为例,截取文丘里管不同横向截面,观察液相含量不断增大时湿气测量装置的分离效果,结果如图5所示。其中:a为距离旋流器25 mm处横截面(即pA取压点所在横截面);b为文丘里管收缩段处横截面;c为文丘里管喉部某一横截面(即pB取压点所在横截面)。
从图5可以看出,湿气在经过旋流器之后不仅有良好的分离效果,也可以将流型转换为强制环状流。这是因为湿气在经过旋流器后,由于气液两相密度差异较大,从而产生的离心力不同,湿气被分离成均匀的气相和液相,密度较大的液相产生较大的离心力被甩在管壁上形成一层液膜,气相密度小,产生的离心力小,沿管道中心流动,从而形成强制环状流。其中b截面的液膜最厚,这是因为b截面处于文丘里管收缩段,管径渐渐变小,液体容易在此处堆积,由于气体的压缩性远大于液体,气体所占面积变小,从而液膜变厚。c截面的液膜较薄,这是因为湿气经过喉部时,气相速度较大,气相对液相携带能力较强,液相不易在c截面处堆积。
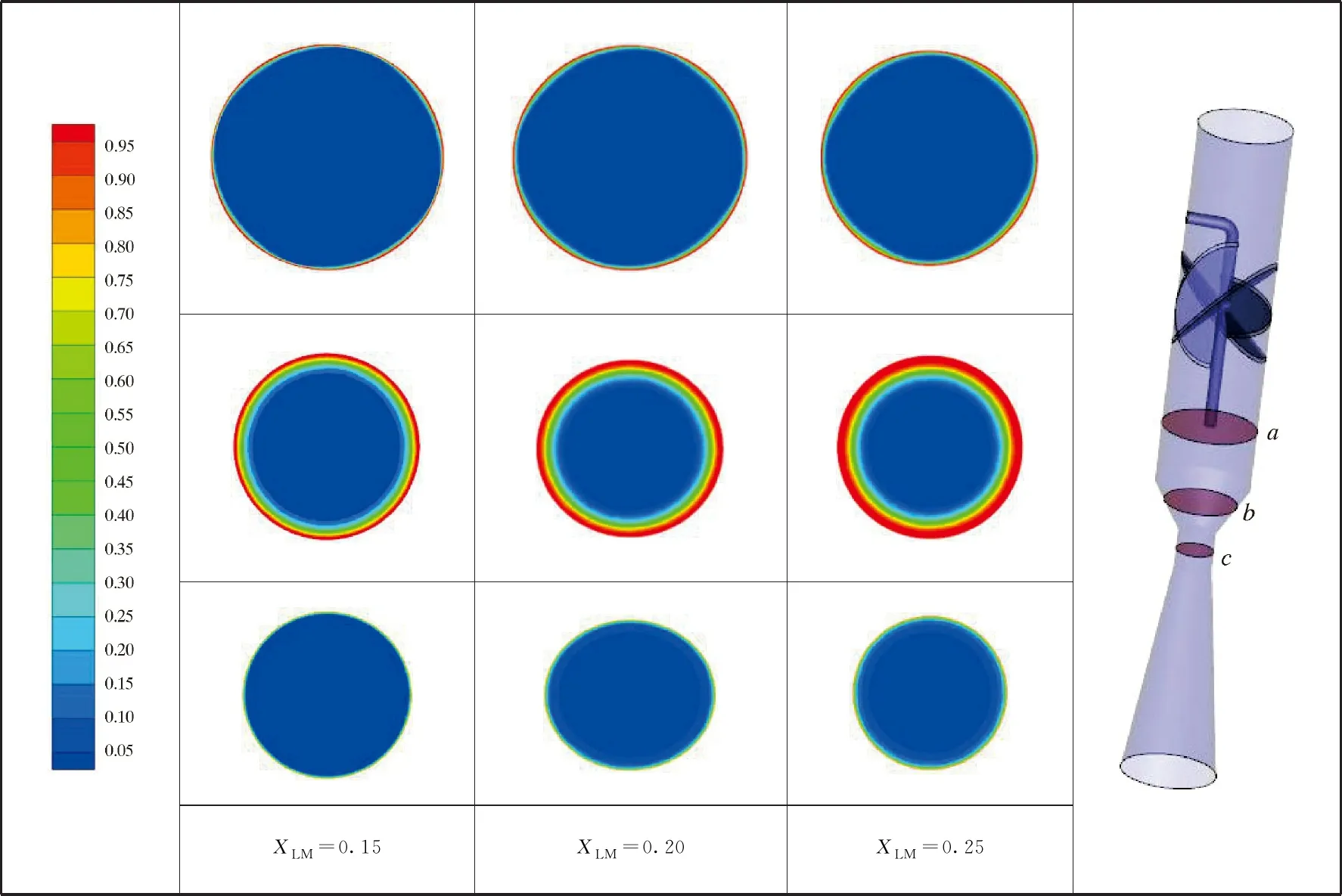
XLM=0.15XLM=0.20XLM=0.25
3.2 离心、节流压差变化规律分析
3.2.1 不同温度、压力条件压差变化规律
图6为离心压差和节流压差随温度、压力的变化规律。从图6可以看出:在保持其他条件不变时,离心压差和节流压差都随温度的升高而增大,这是由于同一条件下,随着温度升高,气相黏度增大,气液两相的摩阻增大,所以节流压差增大;气相表观流速随温度升高而增大,故离心力增大,离心压差增大。离心压差和节流压差随压力增大而减小,这是由于随着压力增大,气相表观流速减小,气相对液相的加速能力越小,气相对液相加速导致的摩擦压降越小,所以节流差压减小;且气相表观流速减小,导致离心力减小,因此离心压差减小。此外,从图6还可以看出,同一工况下的节流压差均大于离心压差。
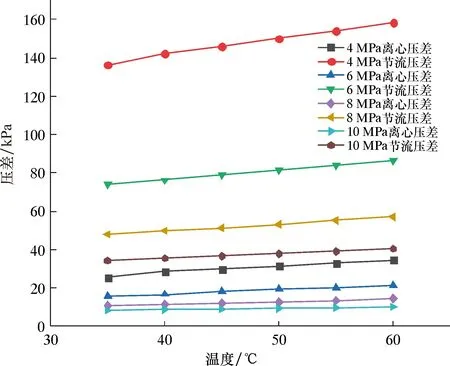
图6 离心压差和节流压差随温度、压力的变化规律Fig.6 Variation rules of centrifugal pressure difference and throttling pressure difference with temperature and pressure
3.2.2 不同XLM和Frg下压差变化规律
图7为离心压差、节流压差随XLM、Frg的变化规律。从图7可以看出:保持其他条件不变的情况下,离心压差、节流压差随着XLM的增大而增大,这是由于液相含率增大使湿气密度变大,湿气惯性增加,流体经过旋流器后所产生的离心力增大,所以离心压差增大;且由于液相含量增大,液相对气相的阻塞作用越大,从而产生的加速压降更大,故节流压差增大。
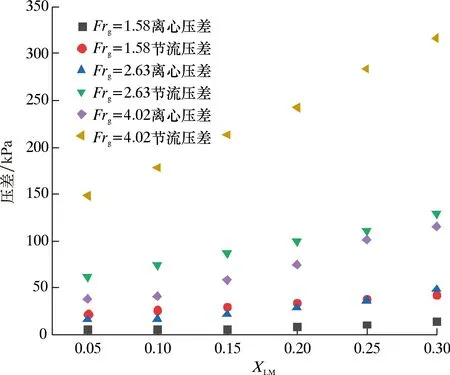
图7 离心压差、节流压差随XLM、Frg的变化规律Fig.7 Variation rules of centrifugal pressure difference and throttling pressure difference with XLM and Frg
保持其他条件不变情况下,离心、节流压差均随着Frg的增大而增大,这是由于气相流量增大,从而湿气经过旋流器后产生的离心力不断增大,所以离心压差增大;且随着Frg的增大气相表观流速增大,气相对液相的加速能力越强,气相对液相加速导致的摩擦压降越大,所以节流压差增大。
值得说明的是,实际生产工况下压差随XLM和Frg的变化规律与常温常压下变化规律基本一致。
3.3 压差比值K的变化规律
图8为同一气相流量与XLM条件下比值K与温度和压力的关系。从图8可以看出:当压力保持不变时,K值随着温度升高而减小;当温度不变时,K值随着压力增大而减小。

图8 K与温度、压力的关系Fig.8 Relationship among K,T and P
图9为同一温度、压力条件下比值K与XLM、Frg的关系。从图9可以看出:在Frg不变的情况下,K值随着XLM的增大而减小;在XLM不变的情况下,K值随着Frg的增大而减小。可以看出,K与XLM有明显的函数关系,因此液相含量可利用K进行测量。
图10是该装置的液气质量流量比wl/wg和压差比值K关系。由图10可以看出:在其他条件保持不变的情况下,wl/wg随K增大而减小;相同条件下,wl/wg随着压力增大而减小。
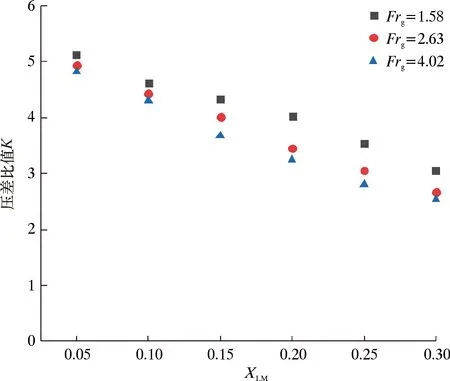
图9 K与XLM、Frg的关系图Fig.9 Relationship among K,XLM and Frg
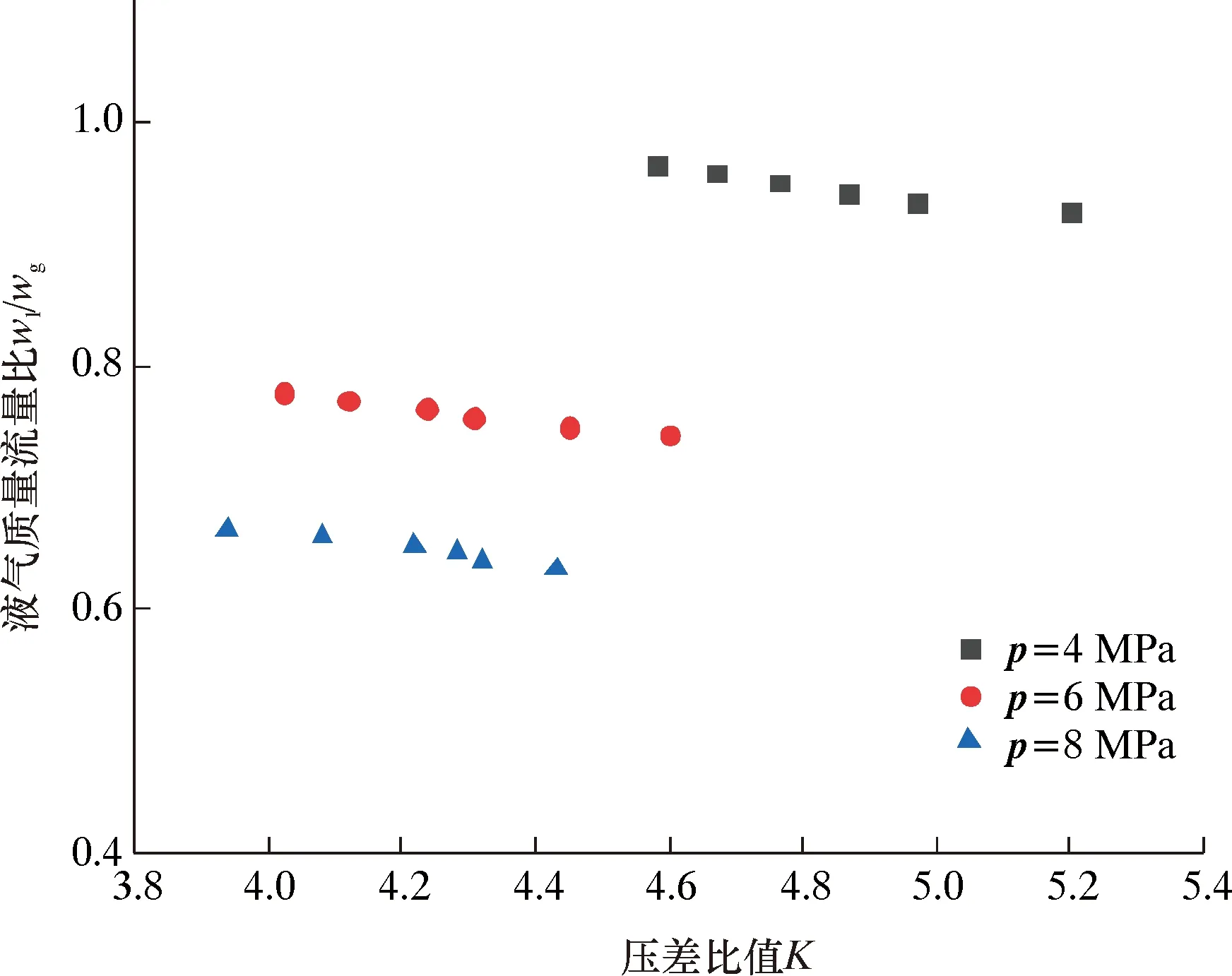
图10 液气质量比与K的关系图Fig.10 Relationship between liquid-gas mass ratio and K
3.4 虚高修正系数Φg的变化规律
图11为虚高修正系数Φg与温度和压力的关系。由图11可以看出:当压力保持不变时,Φg随着温度的升高而增大,但增大幅度较小;在温度保持不变的情况下,Φg随压力增大而减小。

图11 Φg与温度、压力的关系图Fig.11 Relationship amongΦg,T and P
图12为虚高修正系数Φg与压差比值K的关系。由图12可以看出:其他条件不变时,Φg与K有明显的函数关系。Φg随K的增大而不断减小;同一K值下,压力p越大,Φg越小。

图12 Φg和K的关系图Fig.12 Relationship between Φg and K
3.5 虚高模型和液气质量流量比模型
液气质量流量比wl/wg和虚高修正系数Φg不仅与K、Frg有关,压力p及温度T对虚高修正系数Φg也有较大的影响,本文在文献[8]测量模型的基础上考虑了压力与温度的影响,式(19)为本文虚高模拟值与文献[8]虚高模型所计算虚高值的比值L与温度比值Tr(Tr=(T+273.15)/293.15)、压力比值pr的(pr=p/0.101 325)关系式。
L=a+bpr+clnTr
(19)
式中:a=0.087 45;b=-0.000 2;c=0.128 0;pr为气井工况压力和常压比值,取39.47~98.69;Tr为气井工况温度与常温比值,取1.05~1.14。
在文献[8]的虚高模型上加修正系数L,建立新的虚高模型:
Φg=L(a+bKc+dFrgm+nKcFrgm)
(20)
式中:a=4.079 8,b=1.195 7,c=1.244 4,d=4.922 5,m=0.013 5,n=1.145 7。
在已知气体虚高修正系数的情况下,根据1.2小节中的式(3)和式(4)即可得出气体的真实质量流量。式(21)为本文液气质量流量比模拟值与文献[8]液相质量流量模型所计算值的比值J与温度比值Tr、压力比值pr的关系式。
(21)
式中:a=0.137 9,b=-9.817 3×10-5,c=7.962 1×10-8,d=-0.153 1,e=0.018 77,f=0.000 76,g=-0.971 0,pr为气井工况压力和常压比值39.47~98.69;Tr为气井工况温度与常温比值1.05~1.14。
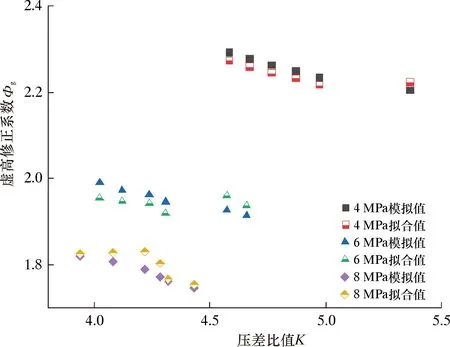
图13 虚高模型拟合曲线Fig.13 Fitting curve of Φg model
在文献[8]的液相质量流量测量模型上加修正系数J,建立式(22)新的液相质量流量测量模型:
(22)
式中:a=0.080 78,b=0.281 9,c=1.871 2,d=0.936 2,m=0.050 5,n=0.266 2。
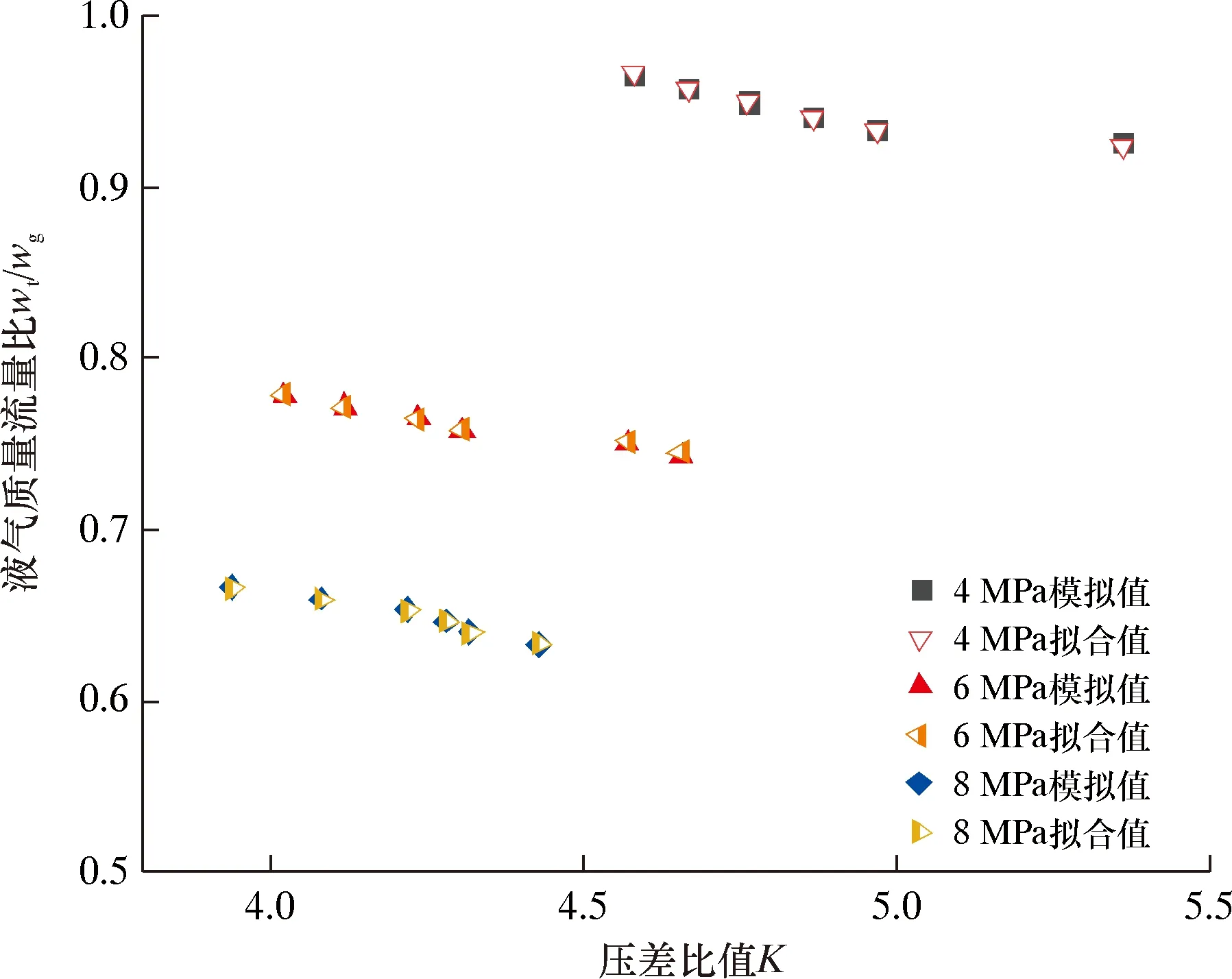
图14 液相测量模型拟合曲线Fig.14 Fitting curve of liquid phase measurement model
3.6 迭代算法
由式 (20)和式(22)知,虚高模型和液气质量流量比模型中的自变量分别为压差比值K、压力比值pr、温度比值Tr和气相弗劳德数Frg,其中pr、Tr都可以通过测量仪表得到,K值也可由式(10)计算获取,但气相弗劳德数Frg在气体真实质量流量已知的情况下才能得到,因此,本文提出了迭代算法实现气液两相的分相测量。由于气体弗劳德数Frg相比于其他参数对虚高模型的影响比较小,所以先假设气体弗劳德数Frg的初值为1,湿气测量流程如图15所示。
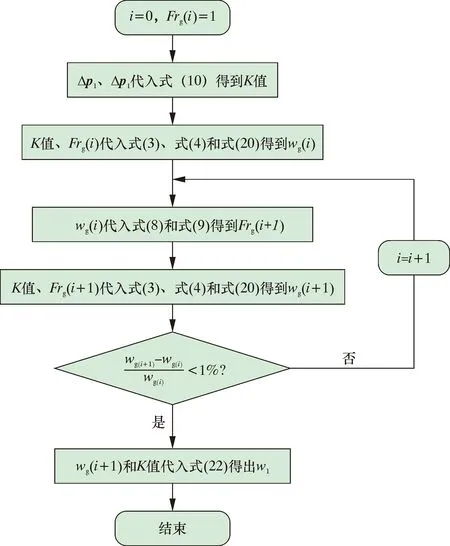
图15 湿气测量流程图Fig.15 Measurement flow chart
4 结 论
(1)基于强制环状流压差特性的湿气测量装置在实际气井工况下表现出了与常温常压状态下相一致的流动特性和规律,即保持其他条件不变情况下,离心、节流压差随着XLM和Frg的增大而增大,虚高修正系数Φg随着XLM和Frg的增大而升高。利用该特性能够实现工况下的湿气测量。
(2)保持其他条件不变的情况下,在实际工况下强制环状流的离心压差和节流压差都随温度的升高而增大,随压力增大而减小,节流压差与离心压差的比值K,随着温度升高而减小,随着压力增大而减小。
(3)基于强制环状流压差特性的湿气测量装置的虚高修正系数Φg随着温度的升高而增大,随压力增大而减小;XLM和压力对虚高影响较大,Frg和温度对其影响较小。
(4)通过分析工况下虚高、液气质量流量比与温度T、压力p之间的联系,建立了一种基于强制环状流压差特性的湿气测量修正模型。
