基于均衡法及数值模拟法的乔诺地下水库资源量论证计算
2022-11-05王友年
王友年
(新疆水利水电勘测设计研究院有限责任公司,新疆 乌鲁木齐 830000)
地下水库在水资源的开发、利用与保护等方面发挥着重要作用,不仅可以解决区域水资源分配不均、水资源短缺等问题,还可以有效防止如地面沉降等环境地质问题的发生[1-2]。乔诺水库工程位于新疆克州乌恰县境内,是克州水资源综合规划确定的调水水源调节水库工程。利用地下水库进行区域水资源调控是地下水开发利用的主要手段之一。因此,开展乔诺地下水库资源量论证计算,进行地下水人工调蓄,对于缓解区域水资源短缺、防止水土流失及改善下游生态环境具有十分重要的现实意义[3-4]。
在国内外众多区域供、需水矛盾愈演愈烈的情况下,水资源的合理开发及利用变得越来越重要[5-10]。部分学者认为开发利用地下水是解决区域水资源短缺的有效途径[5],也有部分学者认为在加强水资源综合管理的前提下,促进地表水-地下水的联合利用也可有效缓解区域水资源短缺的问题[6]。近年来,随着理论认识的不断推进,利用地下水库调蓄逐渐成为解决水资源分配问题的有效方法[7-8]。而地下水库的调蓄库容计算则是建立地下水库的基本条件之一。因此,在进行地下水库建设前需要进行资源量计算,以论证地下水库修建的可行性。对于地下水库资源量计算常用的方法主要有均衡法及数值模拟法[2,9-13]。如杜新强等[10]通过特征水位计算得出库区特征库容。NI et al.[11]基于Visual Modflow软件对威海某河流地下水库库容进行计算后,得出该地下水库具有较大的开采潜力。张源等[2]通过大量的钻孔数据利用GMS软件开展了目标库区调蓄资源量的计算,得到了很好的应用。李凤丽等[12]结合库区水文地质条件,利用数值模拟的方法在计算出库区库容后,经模拟预报后确定了库区合理的开采方案。李安娜等[13]将均衡法与数值模拟法有机结合对目标库区地下水库调蓄库容进行了计算。以上研究均为本文确定乔诺地下水库资源量计算方法提供了思路。
综上所述,地下水库对于缓解区域水资源供需矛盾及水资源合理分配等具有明显优势,因此,需要进一步探索建立地下水库后能否在满足乌瑞克河流域各行业用水的前提下,向阿图什市工业园区供水,以支持工业园区的建设。本文运用GMS软件构建库区地下水流数值模型,并利用均衡法及数值模拟方法同时计算库区地下水资源量,以期为论证乔诺地下水库的可行性及缓解区域水资源短缺等问题提供解决思路。
1 区域地质概况及研究方法
1.1 研究区概况
乔诺水库位于乌瑞克河出山口上游约6km处,行政区划属克州乌恰县。目标库区距阿图什市18km、喀什市20km、吐尔尕口岸36km,南邻314国道。乌瑞克河是克孜河支流卡浪沟吕克河的支流之一,发源于天山南脉阿克巴什阿尤山南坡,地理位置介于东经74°53′59″~75°29′40″、北纬39°38′48″~40°15′52″之间。自源头至出山口河流呈西北—向南偏东走向,出山口以下河流转向南汇入卡浪沟吕克河,河流全长86km,流域面积995km2。
目标库区总地势北高南低,两岸山顶海拔2400~2800m,相对高差300~500m,属低中山区河谷侵蚀地貌,其河谷地貌见图1。库区段河道总体近南北向,河谷底宽300~400m,总体较顺直呈U形河谷,河道自然坡降18‰~22‰。库区两岸坡度较陡,自然边坡 40°~60°,两岸地层岩性为中石炭统及中泥盆统结晶灰岩,中硬岩—软岩类,巨厚层状—厚层状构造,岩层走向与岸坡大角度相交倾向上游,岸坡整体稳定。乌瑞克河水量主要来自冰雪融水和暴雨及地下水补给,汛期主要以冰雪融水补给为主,冬季以地下水补给为主。由于河床由圆状和次棱角状的漂石、卵石、砾石、砂组成,结构疏散,透水性强,河水和地下水转换较频繁。径流季节分布较为集中,年际和年内变化较大。区内地下水总体由北向南径流。
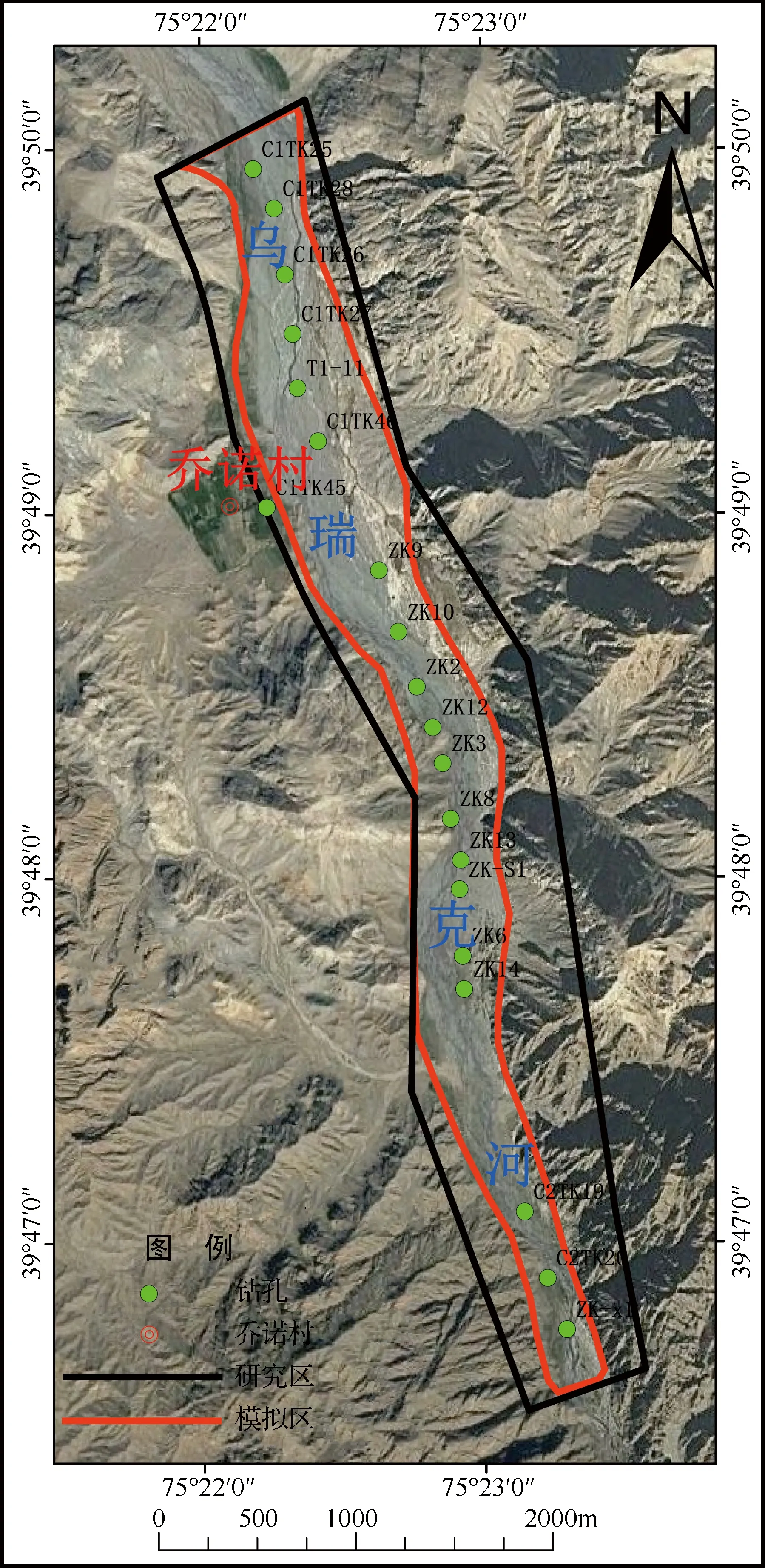
图1 研究区位置
1.2 计算方法
本次为论证计算乔诺地下水库资源量,分别采取均衡法及数值模拟法验证计算目标库区地下水资源量。
1.2.1 均衡法
经实际调查发现库区补给项主要包括侧向流入S1、降雨S2及河道入渗S3等,排泄项主要包括地下水侧向流出S4、渗水管开采S5及蒸发排泄量S6等。依据地下水均衡法[14]对库区地下水资源量进行计算。
ΔS=μFΔH/Δt
ΔS=S1+S2+S3-S4-S5-S6
(1)
式中:ΔS为均衡期地下水水体积变化量,m3/a;μ为含水层给水度;F为库区研究区面积,m2;ΔH为均衡期水位差,m;Δt为均衡期,a。
1.2.2 数值模拟法
本次数值模拟法采用GMS地下水模型系统(Groundwater Model System)进行模拟计算。该软件因具有功能强大的图形界面及可根据库区水文地质条件进行地下水模型构建,进行资源量的模拟计算,在地下水资源量分析计算时被广泛应用[15]。
2 地下水库资源量论证
本次将根据野外实测及抽水试验等数据,利用GMS软件构建库区地下水流数值模型,并运用均衡法及数值模拟法分别计算得出目标库区的地下水资源量,以期为乔诺地下水库的成库论证提供参考依据。
2.1 水文地质概念模型
本次研究区南北长6.5km,东西宽1.2km,总面积约8km2。依据收集的资料、水文地质钻探及物探等工作成果确定库区模拟含水层厚度为120m。上边界为潜水面,为垂向水量交换边界;下边界为隔水边界,无水量交换。结合地下水埋深及地下水流场特征等,确定研究区北部边界由于接受上游地下水侧向径流补给,概化为补给边界;南部边界概化为排泄边界;结合地下水径流方向和初始流场将东、西部边界概化为零流量边界。水文地质概念模型见图2。依据本次勘察及钻孔揭露情况,研究区地层岩性主要为卵砾石及砂卵砾石,且在河谷地带,地下水埋深较浅,含水层无明显且连续的弱透水层,故本次依据含水层划分原则,将研究区在垂向上概化为非均质各向异性潜水含水层。
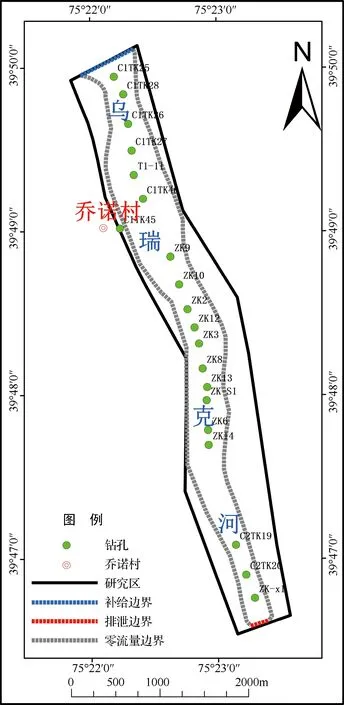
图2 研究区水文地质概念模型
2.2 地下水流数学模型
研究区内地下水含水空间为卵砾石及砂卵砾石,有明显的水力联系,故概化区内地下水流动状态为层流,符合达西定律。通过实际调查发现,虽然研究区内有人工开采,但开采未使用抽水模式,没有影响地下水径流条件,另研究区范围较小,地下水埋深及上下游水位变化不大,河道内地下水与河床具有统一浸润曲线,故可视为三维稳定流。而论证地下水库调蓄时,增加的开采量及调蓄工程将会导致研究区内地下水位发生变化,为三维非稳定流。
综上所述,结合研究区水文地质概念模型,前期模型识别为稳定流,预报计算时为非稳定流,则对应的数学模型选用非均质各向异性三维非稳定流数值模型,模型识别时储存量变化量为零,所建立的数学模型[16]可表示为
(2)
式中:Kxx、Kyy和Kzz分别为x、y和z方向的渗透系数,m/d,Kxx=Kyy;H为水头值,m;q为单宽流量,m3/(d·m);W为源汇项,m/d;μ为给水度;n为边界面的外法线方向;Γ为侧边界;B为底边界。
2.3 时空离散及初始流场
对研究区在空间上的离散包括平面上的网格剖分及垂向上的分层。平面上采用等间距(50m×50m)有限差分的离散方法,共剖分为20736个网格,网格剖分见图3(a),有效模拟面积为3km2。垂向上依照库区水文地质条件共分为3层。本次模拟以2020年5月流场作为初始流场及初始时刻,根据地下水位的观测时间,时间步长以30天为单位,进行模拟及识别。

图3 研究区时空离散及初始流场与边界条件处理示意图
根据研究区实测地下水位,给出的研究区初始流场见图3(b)。根据上述边界条件概化结果在GMS软件中将上边界作为开放边界,底边界处理为隔水边界。由于研究区位于上游河段,其补给项主要包括侧向流入、降雨及河道入渗等,排泄项主要包括地下水侧向流出、渗水管开采及蒸发排泄等。在模型处理时将垂向降雨入渗及人工开采用Recharge模块进行处理,蒸发排泄用ET模块进行处理,河道入渗量、侧向补给及排泄用Specific Flow模块处理。根据库区含水层特征、岩性的空间分布规律及抽水试验获取的水文地质参数确定研究区参数分区,见图3(c)。
2.4 模型识别及验证
结合库区已有水文地质钻孔及抽水试验资料,确定各层水文地质参数,见表1。本次在进行拟合时为消除时间影响,首先进行稳定流初始流场的拟合,并通过不断调整参数对相应参数进行识别。其实测及模拟流场拟合见图4。结果表明本次构建的库区地下水流数值模拟较为可靠,可用于地下水资源量分析与计算。
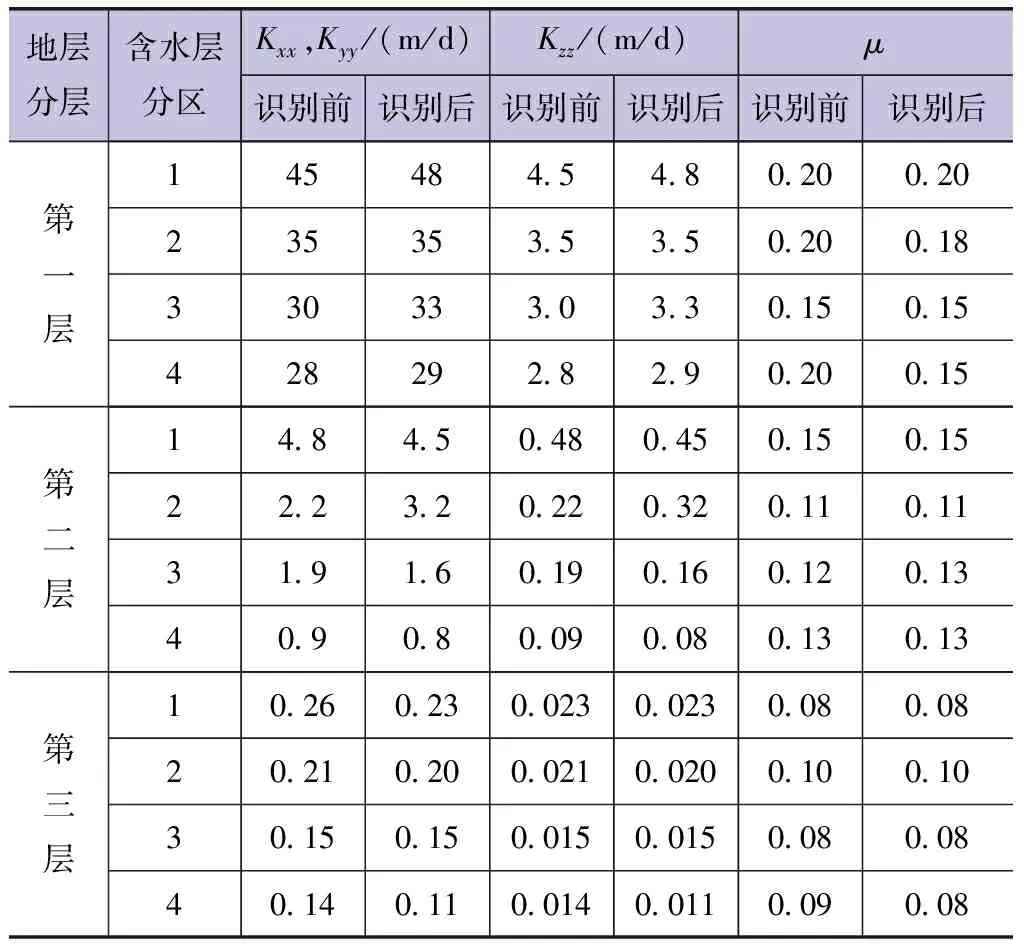
表1 研究区识别前、后水文地质参数
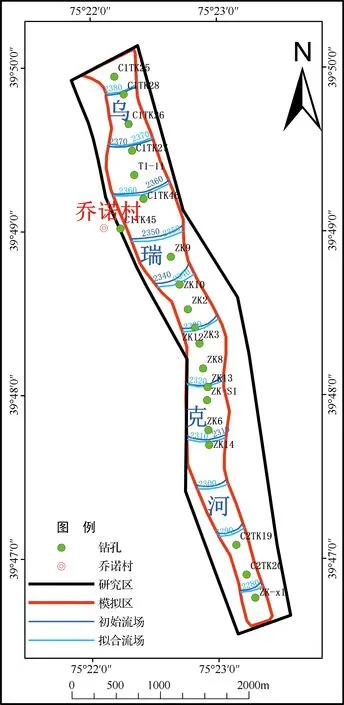
图4 稳定流初始流场拟合图
2.5 库区地下水资源量分析
需要指出的是,由于受现有的工程及实际情况的影响,在建立地下水库后仍将使用已经建成运行的渠首渗管,渗管首部最小自流供水水位为2321m。因此,当水位低于2321m时,地下水将无法自然流入渗管内。故在进行资源量论证时,地下水位保证在2321m之上是重要指标。故本次在进行库区地下水资源量分析时还将计算地下水位2321m以北的区域内的地下水资源量。现运用均衡法及数值模拟法分别计算得出整个研究区及研究区地下水位2321m以北区域的地下水资源量,结果见表2。
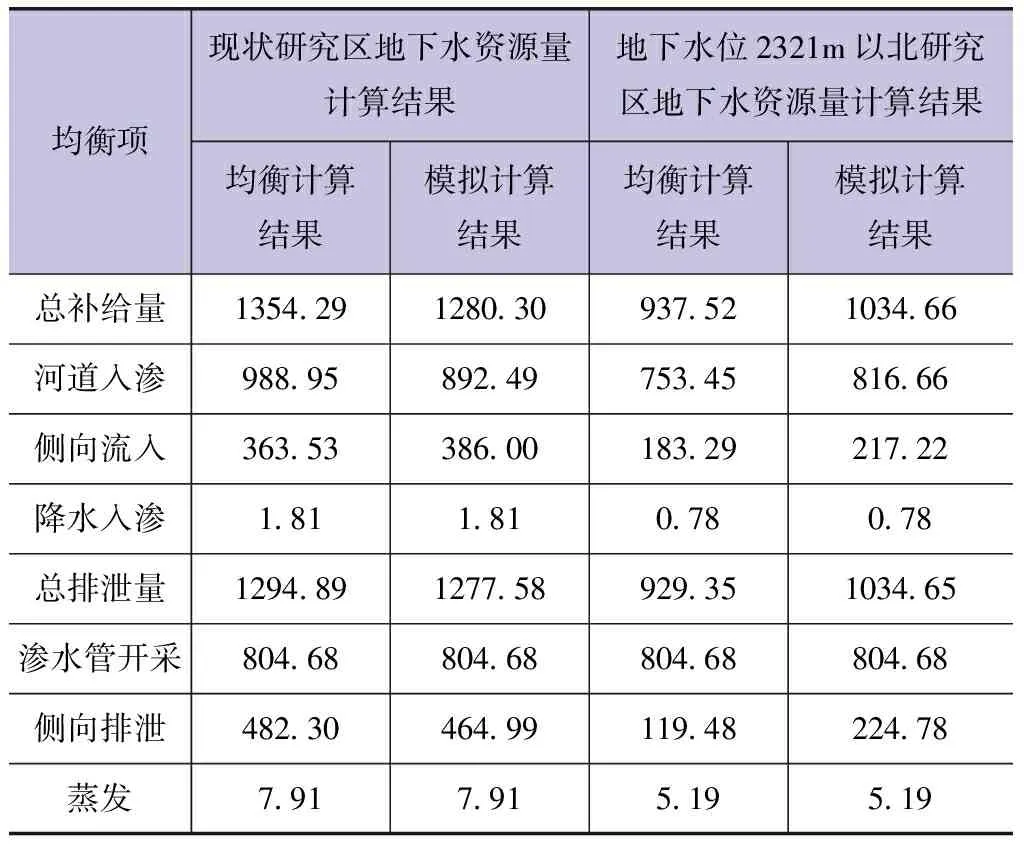
表2 库区地下水资源量计算结果 单位:万m3/年
结果表明,研究区内地下水资源量中河道入渗为主要补给项,渗水管开采为主要排泄项。经均衡法计算得出研究区及地下水位2321m以北区域的地下水资源量中总补给量分别为1354.29万m3/年及937.52万m3/年,总排泄量分别为1294.89万m3/年及929.35万m3/年。经模拟法计算得出研究区及地下水位2321m以北区域的地下水资源量中总补给量分别为1280.30万m3/年及1034.66万m3/年,总排泄量分别为1277.58万m3/年及1034.65万m3/年。库区地下水资源量整体较小,且两种方法计算结果相差较小,也从侧面表明了模型的可靠性。
2.6 目标库区调蓄库容计算
为进一步论证乔诺地下水库的可行性,对目标库区的调蓄库容进行分析计算。地下水库的调蓄能力取决于供水目标、调蓄方案、蓄水能力等。供水目标指地下水库供水需求,对调蓄方案论证起到限制作用,若达不到调蓄目标则不适合修建地下水库。调蓄方案决定了地下水库的蓄水和储水能力,蓄水能力则主要通过地下水库的库容来体现[17]。本次库区调蓄仅就天然条件调蓄进行设计分析。其蓄水能力论证通过调蓄水位、正常水位、死水位对应的地下水库容、可开采资源量及调蓄水量评价结果来分析,目标库区地下水位及库容指标见图5。
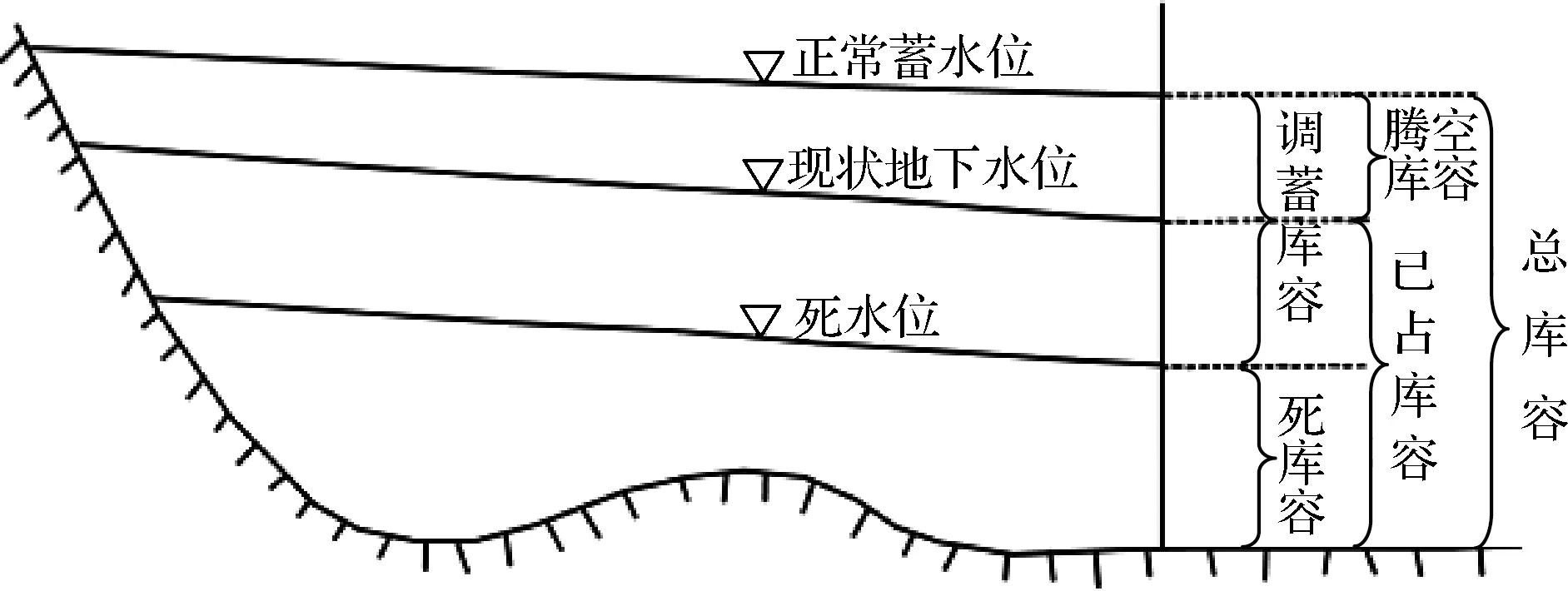
图5 目标库区地下水位及库容指标示意图
对于库区调蓄库容,可根据含水层结构、地下水库体积及给水度确定[13]。其计算公式如下:
V库=μFM
(3)
式中:V库为库容指标,m3;μ为含水层给水度;F为库区研究区面积,m2;M为含水层厚度,m。
结合前文提到的目标库区后期仍将使用已经建成运行的渠首渗管,因此将死水位定为2321m;资料显示,在现状条件下,库区平均地下水埋深为3m;且由于库容较小,在进行论证的过程中,考虑极端条件下若想增大调蓄水量,增加腾空库容,需要将调蓄地下水埋深设计为零,即正常蓄水位为地表高程。则根据式(3)计算得出目标库区的腾空库容与调蓄库容分别为48.59万m3及102.76万m3。
进一步考虑库区外界条件约束,在无人工回补条件下的地下水库开采区为北侧边界至最南侧渗水管处,即研究区2321m水位以北区域。当地下水埋深值等于渗水管埋深时为调蓄下限水位,此时渗水管的出水量为地下水库的最大调蓄能力。结合库区平均地下水埋深为3m,渗水管埋深为4.5m,故本次设计地下水埋深降至4.5m时为调蓄的下限水位。运用模型进行计算,当地下水埋深等于调蓄下限水位时,在无人工回补及有渗水管工程规模条件下,乔诺地下水库的最大开采量为906.39万m3/年,地下水资源量较小,成库条件并不理想。
3 讨 论
本次计算结果可用于论证乔诺地下水库工程的可行性,但通过计算表明目标库区由于受死水位限制其可开采水量较小,该结论可为后续修建地下水库提供参考依据。为分析目标库区地下水资源量较少的原因,本次对比新疆典型地下水库台兰河地下水库。对比发现,乔诺地下水库库区位于上游出山口,储水空间为狭长的河道,储水深度最大为120m左右,储水能力差、库容储量小。刘慧[18]指出台兰河地下水库在洪积扇前缘与细土平原交界带沉积颗粒变细,透水性减弱,地下水流速减慢,可视作天然暗坝。同时存在着天然的阻水构造古木别孜背斜及天然储水空间塔克拉克向斜洼地和巨大的山前冲洪积扇,储水条件较好。上述成库条件是台兰河地下水库和乔诺地下水库库容差异的关键性因素。
同时,本次仅针对天然条件下目标库区的地下水资源量进行分析,但在修建地下水库时还可能会相应地采取一定的工程措施[19-20]。因此,在论证地下水库可行性时还可针对在工程规模条件下地下水库的最大开采量进行预报。同时,也可论证地表水-地下水联合调蓄[21],具体为优先考虑使用地表水(扣除生态基流),若地表水满足供水需求则无须继续论证计算。而当地表水无法满足供水需求的情况下,则可进一步论证天然条件下使用地表水和地下水联合调蓄。即当地表水来水量扣除生态基流不满足供水需求时,还可论证计算在多年平均及不同来水频率下地下水按月是否能够提供地表水不足的部分,而这也可作为后续研究重点。
4 结 论
本文以均衡法与数值模拟法相结合对乔诺地下水库资源量进行论证计算,其结论如下:
a.结合研究区实际情况及水文地质条件,通过均衡法与数值模拟法分别计算出目标库区地下水资源量,结果表明库区地下水资源量较小。
b.经计算得出目标库区的腾空库容与调蓄库容分别为48.59万m3及102.76万m3。
c.目标库区由于受天然条件及死水位限制可开采水量较小,成库条件较差,但今后在考虑地下水库修建时还可进一步开展工程规模及地表-地下水联合调蓄情况下的成库论证。
