基于供区的输电网接线图厂站网格布局算法
2022-11-05蒋正威阙凌燕沙树名刘风剑刘向阳
蒋正威,阙凌燕,沙树名,刘风剑,刘向阳
(1. 国网浙江省电力有限公司,浙江 杭州 310007;2. 南京南瑞信息通信科技有限公司,江苏 南京 210032;3. 河海大学 理学院,江苏 南京 211100)
0 引言
输电网单线图[1-2]也称输电网均匀接线图是电网规划设计、运行监视、理论线损计算、年度运行方式等业务的支撑工具。电网潮流图[3]也称电网潮流单线图[4]是输电网单线图的应用扩展,通常以输电网单线图为底图,对厂站图元作动态叠加电网潮流方向与数值以及线路两侧开关状态,用以电网运行监控和调度大屏展示。到目前为止,实际运行的能量管理系统中大部分潮流图仍依靠人工绘制,而作为这些潮流图的底图,难以在管理信息大区复用。近年来,为满足面向电网统一决策、分级控制、实时协同的一体化运行要求,调控云模型数据云平台按照电网调度通用数据对象结构化设计原则,通过纵向同步工具完成了上下级调度机构之间模型的贯通,形成了全拓扑模型。输电网单线图能够反映电网潮流和主要设备运行状态,宏观展示电网运行态势,辅助电网运行决策,可作为检修可视化、电网运行风险分析等管理信息大区的系统应用入口。另一方面,电网规模的逐年递增,人工维护输电网单线图越来越困难。关于输电网单线图的自动生成早有研究[1-14],主要方向包括厂站位置自动布局和线路自动走线[15-16]。
为了在规定的图幅内生成厂站图元比例适中、布局均匀、线路交叉最少的输电网单线图,厂站节点及T 接节点位置的合理布局是最重要的环节,直接决定了自动成图效果。输电网接线图的自动生成是一个复杂的多目标优化问题[5-8],其中厂站的自动布局难度与厂站数和线路数相关。文献[1]将节点位置定义成网格,将线路总长度作为目标函数,采用罚函数法求得节点布局。文献[9]将潮流图节点自动布局分解为供区布局和供区内变电站布局2 个问题求解。供区布局采用参考地理相对位置、降维简化、人工干预方式生成,供区内部将线路间的交叉点数与线路曼哈顿距离综合起来作为模拟退火的目标函数获得局部最优解。文献[10-12,17]采用斥力-张力模型[18]进行节点自动布局,文献[4]在此基础上采用遗传算法进一步优化。文献[19]对不同电压等级引入不同权重,在节点运动修正方程中引入重力系数,获得结构更为清晰的布局。以上的研究工作均在特定目标下取得了较好的结果[20-23],本文将处理在任意画布下的厂站网格均匀布局,为此提出了厂站网格布局的多目标优化数学模型。
随着中国电网结构日趋复杂,省地级调度机构调管厂站数量监控系统功能日益丰富,对于输电网单线图应用除了拓扑关系的正确展示外,也对图形的简洁美观、逻辑清晰提出了要求。在实际应用中,每个厂站均可根据拓扑关系归集到供区。利用供区的这一特性,本文根据拓扑关系及典型方式下线路两侧断路器运行状态使用二分法将厂站布局到不同的矩形块内。同时,为确保布局区域内的厂站网格均匀布局,本文提出了基于厂站权重系数的力导向网格布局改进算法,其中重新定义了力导向算法中排斥力和吸引力计算公式。通过力导向改进算法实现电网接线图的厂站自动布局。此外,采用网格化布局,即将厂站布局在网格点上,以增加输电网接线图的辨识度。
1 基于供区的厂站网格布局数学模型
针对在任意画布下的厂站网格均匀布局,本文将其建模为带约束条件的多目标优化函数。厂站表示为Vi(i=1,2,···,N), 厂站Vi的平面坐标表示为(x(Vi),y(Vi)), 厂站间线路表示为Line(Vi,Vj)(i≠j),布局区域的宽度和高度为W和L。布局优化的目标为:供区布局合理、无厂站间重叠、布局区域内厂站网格均匀分布、线路的交叉尽量少、线路长度合理。具体描述如下。
(1)布局区域划分合理度E1。布局区域划分合理度是厂站供区划分合理性的衡量指标。在供区面积和供区形状2 个因素的影响下,计算布局区域划分合理度E1为

式中:λ11,λ12为权重系数;n为供区的个数;Ni为第i个供区的厂站个数;Si为第i个供区的实际面积;ρ为理想密度;N为厂站总数;Ri为第i个供区的边长比例,大小为供区宽度和高度中最大值与最小值之比。当供区内厂站实际密度与理想密度的距离较大、供区边长比例过大时,布局区域的划分不合理,反之,布局区域划分合理。
(2)厂站分布均匀度E2。厂站分布均匀度是衡量厂站分布均匀性的指标。先从水平方向均匀地划分布局区域,再从竖直方向均匀地划分布局区域,统计每个区域块内厂站个数。其计算公式为
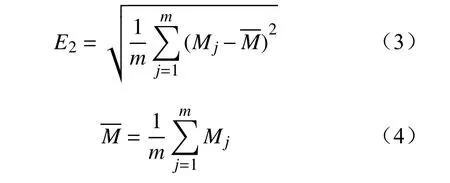
式中:m为均匀划分布局区域得到的区域块数;Mj为第j个区域块内的厂站数目。厂站分布标准差越大,不同区域块的厂站数目越不均衡;反之,厂站分布整体上越均匀。
(3)线路交叉值E3。先判断任意两条线路是否存在交叉点,再统计所有的交叉数目,即获得线路交叉值。线路交叉值越小,线路走向越清晰,因此应当尽量减少线路交叉。
(4)线路长度合理度E4。线路长度合理度是衡量线路长度合理性的指标,过长或过短的线路均会影响布局效果。其计算公式为

式中:Lm为所有线路长度的平均值;k为厂站理想距离,其值大小由式(9)计算可得。E4越大,表明线路长度越不合理,反之则表明线路长度相对合理。
以上是本文优化的主要目标,无厂站间重叠、厂站网格分布则是优化上述目标时必须达到的条件。具体包括:(1)无厂站间重叠:厂站间重叠指两个厂站的坐标相同。厂站重叠会导致布局结果无法使用,因此不允许出现厂站间重叠的情况。(2)厂站网格分布:厂站网格分布指所有厂站分布在布局区域的整数网格点上。厂站网格分布可以呈现出规整的厂站分布效果,因此本文希望实现厂站网格分布。
基于以上优化效果分析,本文优化目标函数为

式中:λ1、λ2、λ3、λ4为权重系数;E1、E2、E3、E4分别为布局区域划分合理度、厂站分布均匀度、线路交叉值、线路长度合理度;Vi、Vj分别为第i、j个厂站的位置; Z为整数集。在平面直角坐标系中,带约束的多目标函数很难使用传统方法直接求解。因此,本文使用力导向网格布局改进算法进行近似优化求解。
2 力导向算法及其改进
2.1 F&R 算法简介
F&R 算法[18]主要包括3 个部分:吸引力的计算、排斥力的计算、计算节点在合力下的移动距离并用模拟退火算法控制节点的最大位移。F&R 算法并没有考虑更复杂的情况,因此当节点超过一定数目时,其求解的布局效果并不好[24-25]。下节将改进F&R 算法,以适应针对供区的网格均匀布局、任意区域布局等其他条件。
2.2 力导向网格布局改进算法
2.2.1 预处理
在自动布局的过程中,厂站布局效果很大程度上取决于厂站的初始坐标。F&R 算法中节点的初始坐标由算法随机分布,布局的结果很不稳定,因此本文将厂站的地理坐标应用到厂站坐标的初始布局中,另外可大致确保厂站的地理相对位置。厂站的地理坐标分布不均匀,并不能直接用作厂站的初始坐标。本文将厂站的地理坐标映射到布局区域的一定范围内。
2.2.2 吸引力的计算
F&R 算法中引力公式计算一般情况下两个厂站间的吸引力,即两个厂站之间有线路相连时,引力的大小和两厂站间距离的平方成正比,否则,两个厂站之间没有吸引力。计算引力Fa为

k的计算和布局区域的面积以及厂站的个数有关。本文在计算k时引入了缩小尺度,目的是为了让所有厂站分布在布局区域的合理范围内,即
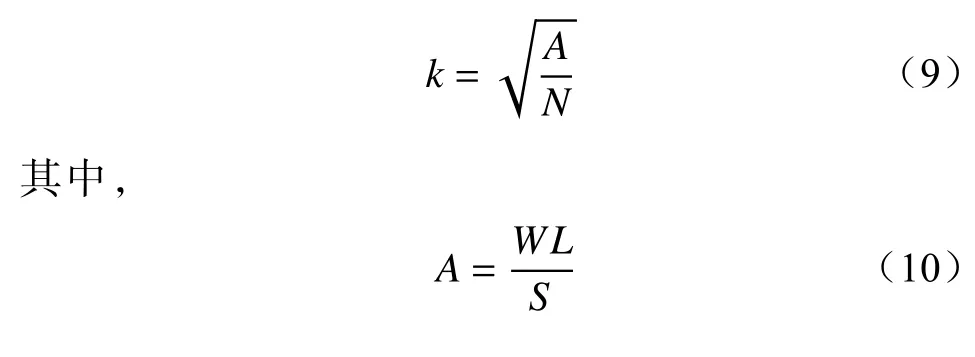
式中:S为计算理想距离时的缩小尺度。
2.2.3 排斥力的计算
在F&R 算法中,排斥力的计算在所有的节点间进行,并且排斥力的大小仅仅和节点的距离有关。当节点数目较多、连接密切时,排斥力产生的布局效果并不好。本文考虑了两个厂站距离过近和厂站出线度对网格均匀布局的影响,在排斥力计算过程中引入了新的力。此外,为了防止厂站被排斥到区域边缘,本文只计算厂站固定范围内的排斥力Fr,即
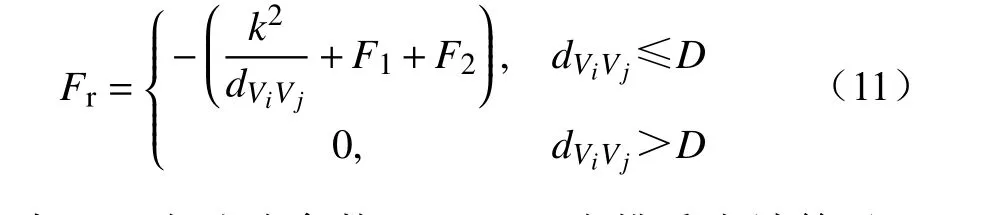
式中:D为试验参数;F1,F2为排斥力计算过程中引入的新力。
随着算法循环进行,整个系统逐渐趋于稳定,厂站的位置也逐渐固定,因此布局不合理的两个厂站越不容易被排开。本文使用指数型函数加大距离过近的厂站间的排斥力,计算F1的公式为
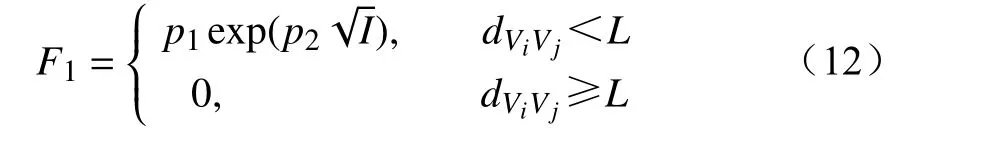

式中:dm为出线度较大厂站的阈值,为试验参数;dg(Vi)和dg(Vj)分别为厂站Vi和Vj的实际出线度。
2.2.4 厂站的偏移
本文将厂站受到的所有力合成,得到每个厂站所受合力F,将F分解成x轴方向上的力Fx以及y轴方向上的力Fy,然后利用式(14)计算厂站在x轴方向上移动距离Δdx和y轴方向上移动距离Δdy。
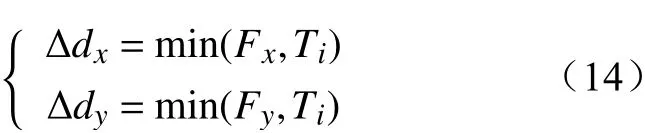
式中:Ti为第i次迭代时模拟退火函数的取值。
本文使用模拟退火函数控制厂站的最大位移,目的是防止厂站被排斥到布局区域边缘,影响到厂站网格均匀布局。模拟退火函数的选取会直接影响到布局效果,因此本文使用指数型模拟退火函数控制厂站的最大位移,即
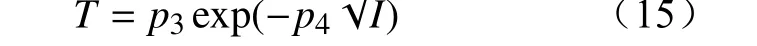
式中:p3和p4为实验参数。指数型模拟退火函数式(15)使厂站在循环初期快速地排开,在循环后期快速地趋于稳定状态。考虑到布局区域的宽度和高度可能不同,本文使用两向模拟退火算法,即式(15)控制厂站在x轴和y轴方向上的不同最大位移,参数p3的取值受布局区域宽度和高度的影响。
上述循环迭代结束后,按照四舍五入的方式对厂站的横纵坐标取整,控制厂站网格布局。由于力F1的作用,厂站坐标取整后确保不会重叠。
3 基于供区划分的厂站网格均匀布局
3.1 供区的布局区域划分
在划分布局区域的过程中,本文先使用力导向网格布局改进算法计算供区中心点坐标和供区的相对位置,再使用二分法对布局区域进行划分,同时保证供区位置的合理性。
3.1.1 供区坐标和供区相对位置的计算
本文使用力导向网格布局改进算法计算布局在合理位置的供区中心点,并将供区中心点的相对位置作为供区的相对位置,其中供区中心点设置为Vci(i=1,2,···,n),供区中心点的设置是为了更好的划分区域,但并不参与到厂站的布局过程中。考虑到划分布局区域的特殊性,这里需要对力导向网格布局改进算法做如下调整。
在预处理过程中,将相同供区的厂站地理坐标的平均值映射到布局区域,作为供区中心点的初始坐标。供区中心点的初始坐标并没有考虑供区间的复杂关系,因此不能直接用于布局区域的划分。经过力导向网格布局改进算法的多次迭代,供区中心点布局在合理的位置,同时供区的相对位置也更加合理。计算两个供区中心点间吸引力时,若两个供区中心点对应的供区间存在两个厂站有线路相连,则认为是两个供区中心点间有线路相连;否则,无线路相连。
理想距离k的计算不仅要考虑供区中心点的数目,还要考虑供区大小的影响。本文在计算供区中心点的理想距离时引入了权重,因此计算式为

式中:n为供区中心点的个数;w为供区内厂站个数与所有供区厂站个数的均值的比值。
3.1.2 划分布局区域的二分法
获取供区的相对位置后,本文采用二分法的思想对布局区域进行划分,即根据供区的相对位置,对布局区域一分为二,直到所有供区划分完毕。
根据供区的相对位置划分布局区域的时候,首先将供区中心点合理分成2 部分,再根据两部分供区中心点对应供区内厂站的个数比,从布局区域的长边进行划分。其中,将供区中心点合理地分成2 个部分:首先将供区中心点映射到长边对应的坐标轴,并对映射后的供区中心点从小到大排列,再分2 种情况考虑:供区中心点个数为2n时,将前n个供区中心点分到一个部分,后n个供区中心点分到另一个部分。供区中心点个数为2n+1 时,将前n个供区中心点分到一个部分,后n个供区中心点分到另一个部分。分别计算两个部分供区中心点对应的供区内厂站个数,将第n+1 个点分到厂站个数较少的部分。
3.2 厂站布置的全局优化
在厂站布置的全局优化过程中,本文使用力导向网格布局改进算法处理布局区域内的所有厂站。由于要将厂站布局在供区内的网格点上,布局区域内的厂站间吸引力的计算依旧使用式(7),但不同的是,供区间厂站的距离一般会大于供区内厂站的距离。因此,这里对理想距离k的计算做了如下改变:当Vi和Vj同属一个供区时,使用式(9)和式(10)计算供区内厂站的理想距离k。当Vi和Vj分属两个供区时,理想距离k的大小与供区对应的供区中心点间的距离dVCiVCj有关。其计算公式为

式中:λ为权重系数。
3.3 基于供区划分的厂站布局算法
本文将力导向网格布局改进算法应用到基于供区划分的厂站网格均匀图的自动布局中,最终使所有厂站均匀地分布在供区内的网格点上。根据以上分析和基于供区划分的厂站网格均匀布局算法的描述,该算法的流程如图1 所示。
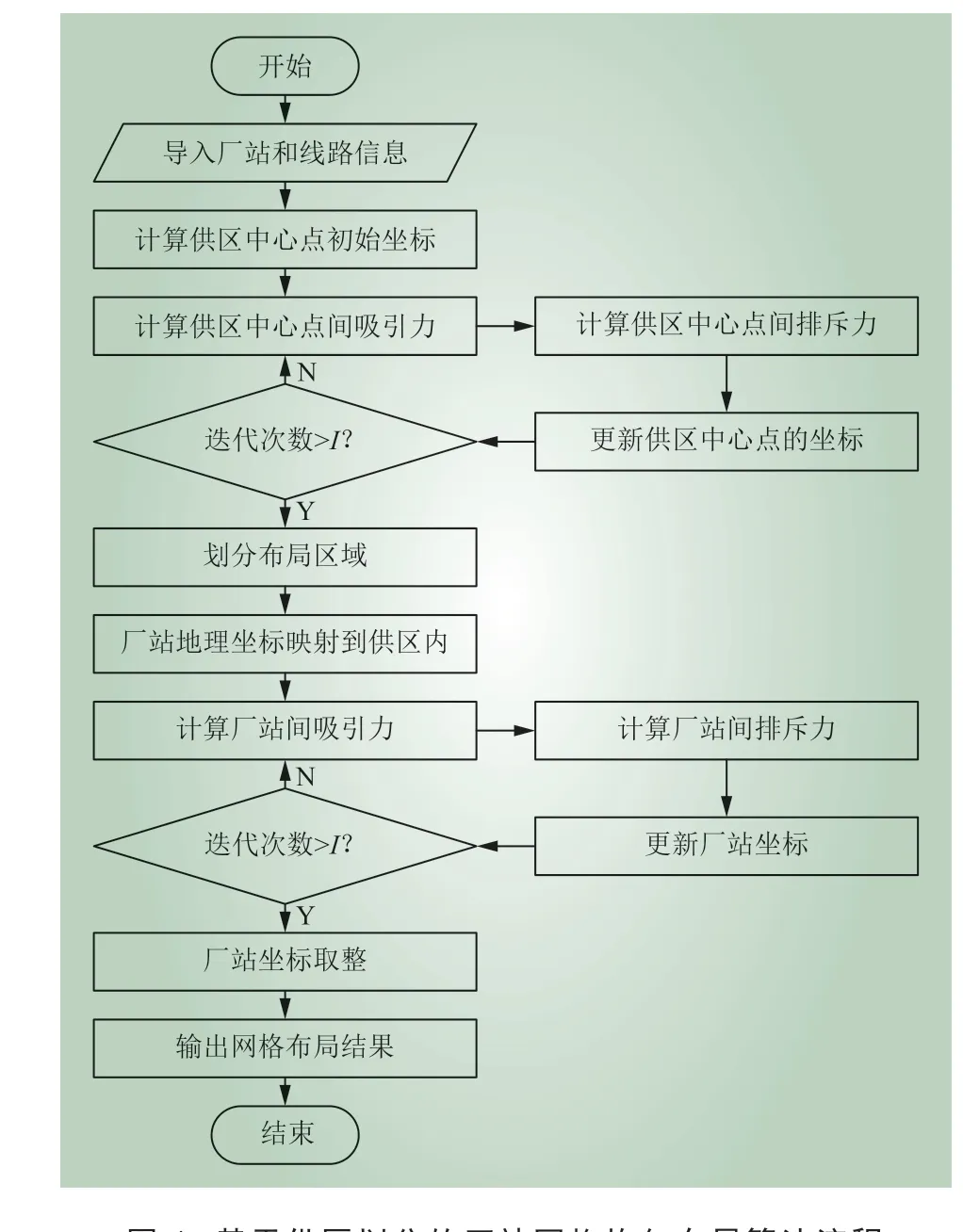
图1 基于供区划分的厂站网格均匀布局算法流程Fig. 1 Flow chart of power station grid layout algorithm based on supply area division
4 实验分析与结果
本文使用某省部分实验数据进行了基于供区划分的厂站网格均匀图布局。硬件配置环境为CPU(i7-8700)+ 内存(8 G)。算法的迭代次数I设置为800;缩小尺度S设置为1.5;在排斥力计算过程中,D设置为3k;dm设置为5;在两向模拟退火算法中,p3的大小设置为布局区域边长的1/10,p4设置为0.2。
4.1 供区布局结果及分析
本实验测试了供区的布局效果,其中实验数据包含了4 个供区的58 座厂站和139 条输电线路,区域的宽度和高度分别设置为11、9。在没有使用力导向网格布局改进算法的情况下,基于二分法的供区布局效果并不好,供区间线路产生了无法避免的交叉;而使用力导向网格布局改进算法处理供区布局后,布局区域划分合理度E1的值由1.173 0 降为1.132 5,供区的相对位置合理,有效减少了供区间的线路交叉。
4.2 线路交叉值测试结果及分析
为了分析力导向网格布局改进算法在减少交叉方面的作用,本实验测试了迭代过程中线路交叉数的变化。图2 显示了线路交叉数的迭代变化过程,其值一开始迅速减小,随着迭代次数的增加,线路交叉数稳定在合理范围内。
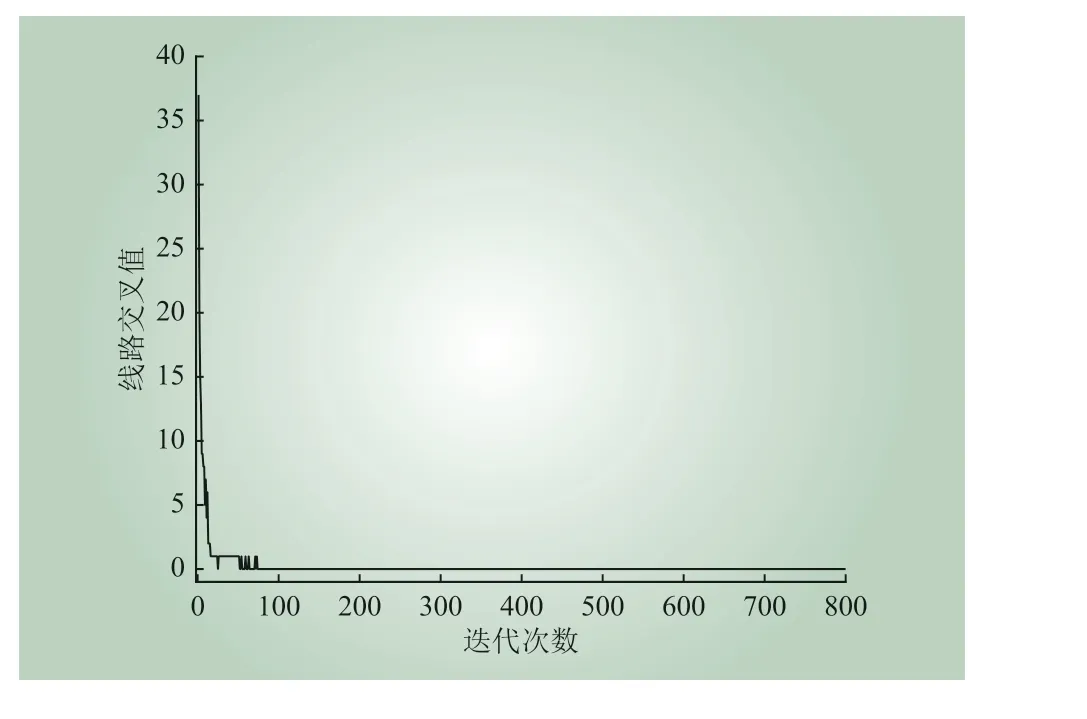
图2 迭代过程中线路交叉值的变化Fig. 2 Variation of line crossing value in iteration process
4.3 厂站分布均匀度测试结果及分析
本实验使用式(3)测试了力导向网格布局改进算法在控制厂站均匀分布方面的性能,得到了如图3 所示的结果。
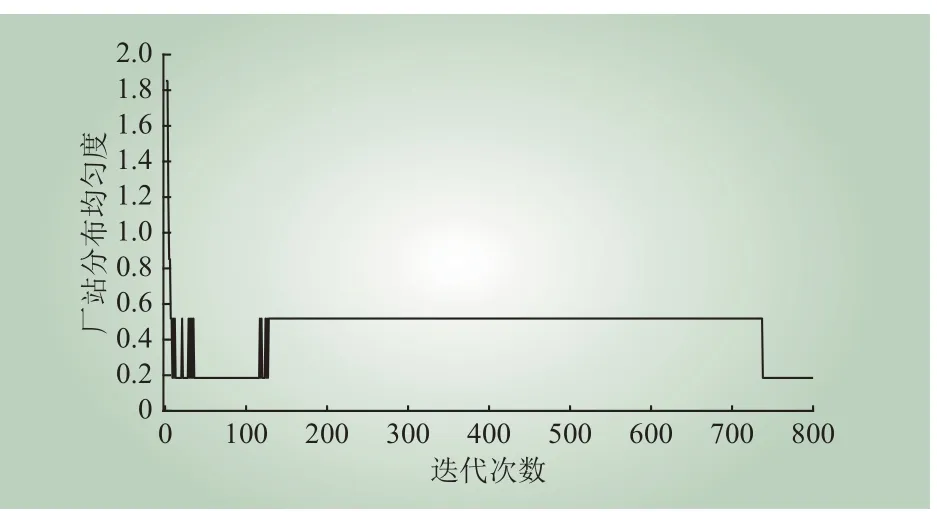
图3 迭代过程中厂站分布均匀度的变化Fig. 3 Variation of station distribution uniformity in iterative process
厂站网格布局数学模型为多目标函数,且主要目标为减少交叉,因此厂站分布均匀度并没有呈现出稳定的下降状态,但交叉数目快速减少。
4.4 线路长度合理度测试结果及分析
本实验计算了每次迭代中所有线路长度合理度的大小。图4 显示了所有线路长度值的迭代变化过程,该值在一开始迅速减小,之后随着迭代次数的增加逐渐减小,最终趋于稳定状态。
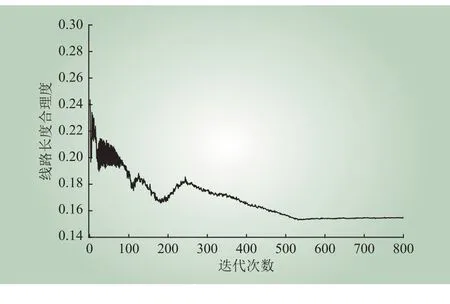
图4 迭代过程中线路长度合理度的变化Fig. 4 Variation of line length in iteration process
4.5 厂站网格化布局处理结果及分析
本实验使用电网数据进行了基于F1的厂站网格布局测试,局部结果对比如图5 所示。在未使用力F1控制厂站网格布局时,37 号与44 号厂站、42 号与43 号厂站取整后出现了坐标重叠问题。相反,使用力F1控制厂站网格布局后,厂站坐标取整后如图5 d)所示,图5 中不存在厂站重叠问题,因此,力F1有效地控制厂站分布在布局区域的网格点上。
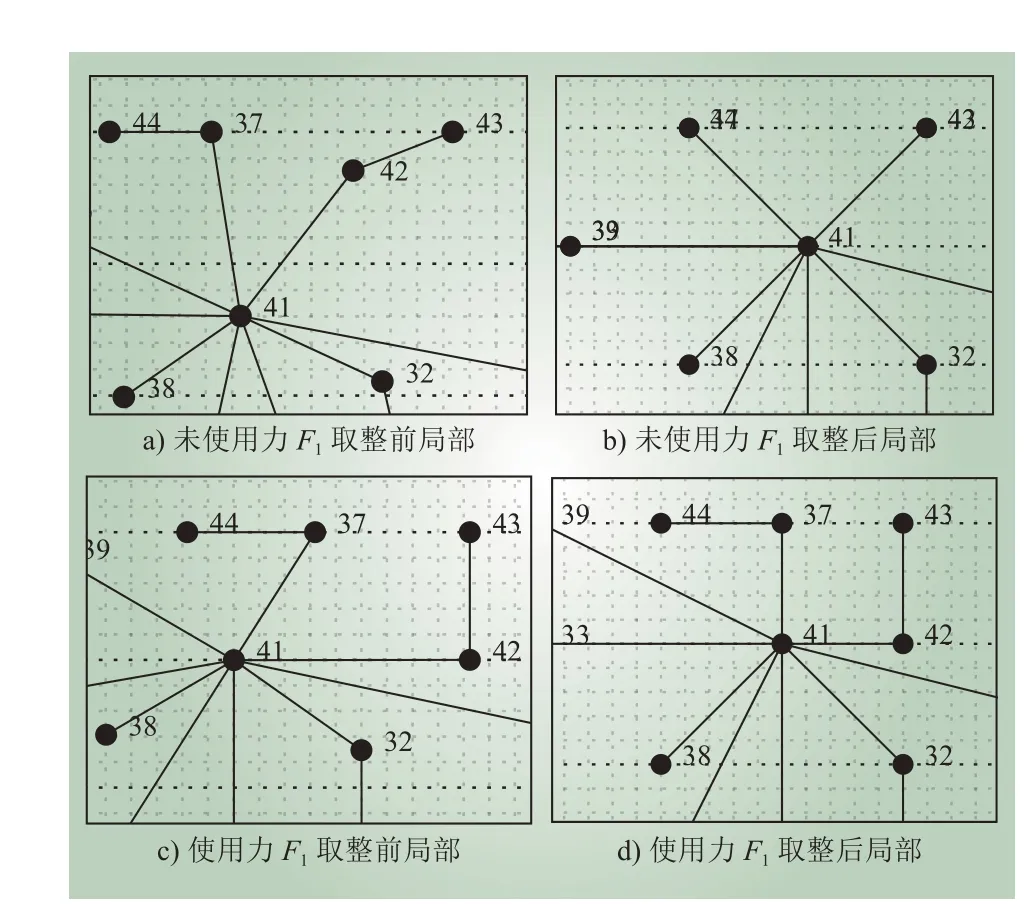
图5 网格处理局部结果对比Fig. 5 Comparison of local results of grid processing
4.6 实验结果及分析
为了测试本文算法的处理效果,对包含58 座厂站和139 条输电线路的数据进行了基于供区划分的厂站网格均匀图的自动布局测试。整个算法耗时20.06 s,实验结果如图6 所示。
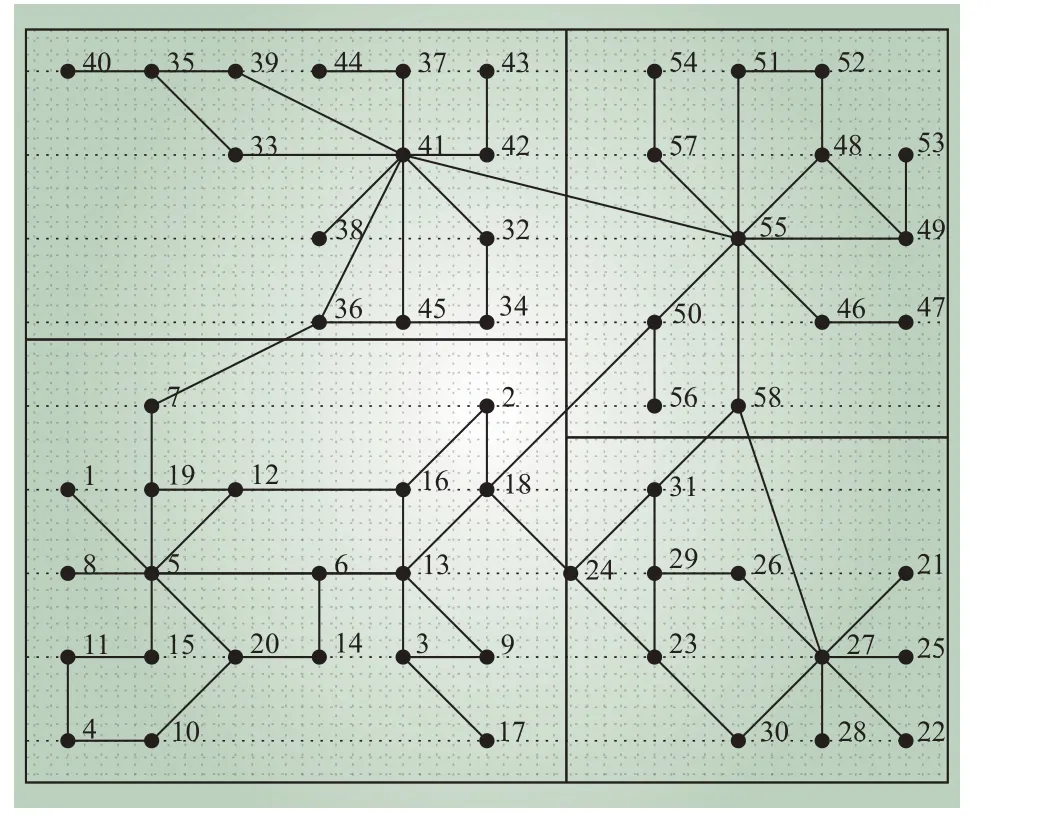
图6 58 座厂站网格布局结果Fig. 6 Grid layout of 58 stations
由图6 可以看到:布局区域划分的大小合理并且正确反映了供区之间的位置关系,厂站比较均匀地分布在供区内的网格点上,没有厂站坐标的重叠和线路的交叉点。此外,厂站网格均匀图的结构合理,能够清晰地辨别出厂站之间的连接关系。但是,图6 中左上角的厂站分布不够均匀,存在较大的空白区域,若能对部分厂站进行局部优化,则整体布局效果会更好。
4.7 基于真实数据的厂站网格布局
为了更好地测试算法的处理效果,这里使用了复杂的电网数据,包括7 个供区的106 座厂站和247 条线路。整个算法耗时96.31 s,布局区域的宽度和高度分别设置为17、13,其他参数取值均与图6 相同。实验结果如图7 所示,供区的相对位置比较合理,供区内的厂站网格分布也比较均匀,能够清晰地分辨出线路走向,线路交叉比较少。某省调结合调控云数据云平台,其应用界面如图8 所示。

图7 106 座厂站网格布局结果Fig. 7 Grid layout of 106 stations
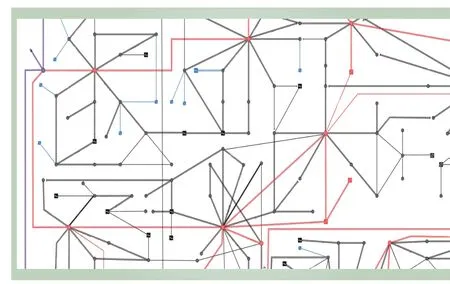
图8 电网接线图应用于潮流可视化的界面Fig. 8 UI of power flow visualization with power grid diagram
5 结语
针对供区划分的厂站网格均匀图的自动布局,本文提出了力导向网格布局改进算法。力导向网格布局改进算法引入了厂站权重系数,重新定义了排斥力和吸引力的计算方法,采用两向模拟退火算法控制厂站布局均匀。基于供区划分的厂站网格均匀图的自动布局分为2 个阶段:供区的布局区域划分和厂站的全局优化。将本文算法应用到某省厂站网格均匀图的自动生成,表明本文算法得到的网格均匀图中厂站能够比较均匀地分布在供区内的网格点上,可以满足用户的实际需求。下一步将在本文算法基础上厂站优化布局的同时对线路进行横平竖直优化布局。
