基于改进智能算法反演概率积分参数

刘 双 刘 宇

（1. 安徽理工大学空间信息与测绘工程学院，安徽 淮南 232001；2. 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室，安徽 淮南 232001；3.安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心，安徽 淮南 232001）

概率积分法广泛应用于矿区开采沉陷预计分析，其理论模型简单可靠[1]，而求取概率积分参数是预计矿区地表移动沉陷的前提。智能算法是目前进行参数反演的主要方法，如：遗传算法、果蝇算法[2]等。用花朵授粉算法（Flower pollination algorithm, FPA）反演概率积分参数尚未有学者研究，但FPA 算法易陷入局部最优解且收敛速度慢[3]，所以本文建立差分进化花粉算法（Differential evolution flower pollination algorithm,DEFPA）反演概率积分参数模型，通过矿区实例证明了DEFPA反演概率积分参数的精度更高、效果更好。

1 DEFPA 反演概率积分参数模型

1.1 DEFPA 算法模型

设目标函数f（x），初始化种群规模为N，向量xn=（xn1,xn2,…,xnθ,…,xnd）表示种群中每个花粉，其中xnθ（θ=1,2,…,d）是第n个花粉第θ维的位置，d是参数维数[4]。具体步骤如下：

（1）创建随机初始化种群，包括转换参数p，最大迭代次数Ni，种群规模N，维度搜索变量d。

（2）记录每个花粉配子适应度值，求解最优值g*。

（3）抽取随机检查概率rand，若rand＞p，进行自花授粉，更新公式为：

式中：g*为种群最优花粉；Γ（λ）为标准伽马函数，λ取1.5 最好[5]。

（5）记录新的适应值得到最新解。若新解比最优解效果好，则用新解代替最优解并更新种群，最后得到当前最优解。否则，转到第（3）步。

（6）对当前最优值进行变异、交叉、选择过程，得到最新解。

（7）得到全局最优解g*，程序结束。

1.2 适应度函数

2 模拟实验

2.1 设计工作面的地质采矿条件和沉陷预计参数

地质采矿条件：煤层厚度2.5 m，倾角3°，平 均 采 深H=300 m， 走 向 长D3=800 m， 倾 向长D1=400 m。概率积分法预计参数：下沉系数q=0.8，拐点偏移距S1=S2=S3=S4=60 m，主要影响角正切tanβ=1.5，水平移动系b=0.3，下沉影响传播角θ=85°。在开采区域内按走向线设计B 观测线，走向线长1280 m。按倾向线设计T 观测线，倾向线长880 m。模拟观测站的点布设如图1。

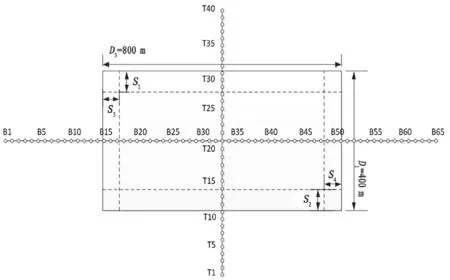
图1 模拟工作面地表监测点位置分布表

2.2 DEFPA 反演参数准确性实验分析

将DEFPA 算法模型反演的概率积分参数与设计值比较，见表1。

根据表1，计算后的相对误差绝对值均不超过5%，DEFPA 算法模型反演的拟合下沉值和水平移动值标准差为5.84 mm，准确性较高。

表1 DEFPA 概率积分法反演参数准确性分析

2.3 DEFPA 反演参数抗随机误差实验分析

观测线监测点的下沉值增加10 mm 的中误差、水平移动值减少5 mm 的中误差。将修改后的下沉值和水平移动值导入算法，结果见表2。

根据表2，DEFPA 反演参数值相对误差绝对值均低于3%，DEFPA 反演概率积分参数的抗随机误差能力较强。因此，在外业条件困难情况下可适当降低观测精度。

表2 DEFPA 概率积分法反演参数抗随机误差分析

2.4 DEFPA 反演参数抗粗差实验分析

沉陷区拐点处和最大下沉点处对结果影响相对较大，将观测线拐点处和最大下沉点处的观测数据各增加200 mm 的中误差，用DEFPA 反演概率积分参数，结果见表3。

根据表3，在增加重要观测点中误差的情况下，DEFPA 反演参数波动非常小，对结果的影响不大，因此，DEFPA 反演参数抗粗差能力较强。

表3 DEFPA 概率积分法反演参数抗粗差分析

2.5 DEFPA 反演参数抗观测点缺失干扰分析

剔除观测线上50%观测点，用DEFPA 反演概率积分参数，结果见表4。

根据表4，DEFPA 反演的参数值相对误差绝对值均不超过3%。在随机剔除一半观测数据情况下，DEFPA 反演参数的相对中误差虽出现波动，但是所有概率积分参数相对中误差均不超过3%，对结果影响较小。

表4 DEFPA 概率积分法反演参数抗观测点缺失干扰分析

3 工程实例

淮南顾桥矿区南三1613（1）工作面采用综合机械化掘进，全部垮落法管理顶板。1613（1）工作面煤厚1.0～4.2 m，平均 2.8 m，平均采高2.9 m；倾角0～6°，平均3°。根据井上下对照图，回采工作面煤层埋深618～723 m，平均约668 m。工作面实际回采面的倾向长1528 m，回采走向长约251 m，地表平坦，高程在18.0～23.0 m 之间，平均约21.5 m。走向观测线长2020 m，倾向观测线长2508 m。本文以倾向线下沉值和水平移动值为实测观测数据，求取参数见表5。

根据表5，得到DEFPA 和FPA 参数反演的下沉值拟合曲线和水平移动值拟合曲线，分别如图2与图3。

表5 DEFPA 和FPA 算法反演参数对比值

根据图2 与图3，FPA 得出的下沉值和水平移动值的拟合标准差是72.96 mm；相比DEFPA 得出的拟合标准差是67.07 mm，且下沉值绝对误差最大值为209.41 mm，水平移动值的绝对误差最大值为123.93 mm。因此，DEFPA算法反演效果比FPA更好。

图2 DEFPA 与FPA 算法拟合下沉值对比图

图3 DEFPA 与FPA 拟合水平移动值对比图

4 结论

（1）DEFPA 反演概率积分参数有较高的准确性，抗随机误差、抗粗差、抗观测点缺失能力较强。

（2）经工程实例验证，DEFPA 反演得到的下沉值和水平移动值的拟合标准差比FPA 反演得到的下沉值和水平移动值标准拟合差小5.89 mm。