露天采矿爆破振动过程中边坡稳定性极限分析

包有才

（中国建筑材料工业地质勘查中心宁夏总队，宁夏 银川 750021）

不同种类的矿山大量开发，为了节约开采成本，提高开采效率以及矿产资源回收利用率，大部分矿山开采均采用露天开采方式。由于露天开采技术还不够成熟，且露天矿山开采安全与质量受矿山地质因素影响比较大，露天矿山开采面临着多方面的问题，比如边坡覆盖面积广泛、边坡地质结构比较脆弱等，再加上露天开采过程中爆破振动作用力的影响，边坡稳定性已经成为制约露天采矿的重要问题。爆破是矿山露天开采施工过程中一项必不可少的环节，爆破振动波经过岩石传播到边坡内部，从而导致边坡地质内部的剪切强度降低，此外还会对边坡自身产生一定的惯性力，导致边坡表面覆盖的岩土松动下滑，严重时会发生边坡滑坡地质灾害。为了确保露天采矿施工作业能够安全有序地进行，本文提出露天采矿爆破振动过程中边坡稳定性极限分析。

1 分析方法

1.1 建立采矿爆破振动作用下边坡破坏机构模型

边坡地质遭到破坏主要是受到露天采矿爆破振动荷载作用影响，考虑到爆破振动衰减的退耦，对露天采矿爆破振动荷载进行计算，其计算公式如下：

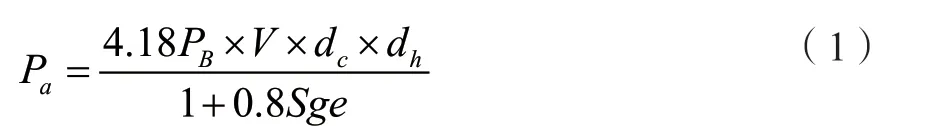
式中：Pa为露天采矿振动爆破荷载；PB为作用在孔壁上的退耦爆破压力；V为爆破速度；dc为露天采矿爆破时装药直径；dh为装药孔直径；Sge为容重[1]。在实际中露天采矿爆破振动作用在孔壁上的压力是会随着时间变化而发生改变的动力荷载，爆破荷载形式近似为扇形冲击波，因此将上述公式调整为：

式中：B为露天采矿爆破振动荷载系数，即每0.1 kg 装药孔内炸药所产生的动压力，通常该系数取值为12 346[2]。基于爆破振动荷载作用下边坡的稳定性遭到破坏，破坏形式主要为剪切破坏形式，其用公式表示为：

式中：F为边坡剪切强度安全系数；s为露天采矿爆破振动过程中边坡破坏面上的剪切强度；v为边坡实际剪切力。当边坡剪切强度安全系数为1 时，即强度折减与边坡剪切强度安全系数相等时，边坡稳定性达到极限稳定状态[3]。当受到露天爆破振动荷载作用，边坡岩土遭到破坏，根据摩尔-库伦屈服条件，对边坡破坏安全系数进行计算，其公式为：

式中：Fs表示露天采矿爆破振动过程中边坡破坏安全系数；c表示边坡岩土黏聚力；φ表示边坡内摩擦角；K表示边坡主应力[4]。根据上述分析建立采矿爆破振动作用下边坡破坏机构模型，如图1。

图1 采矿爆破振动作用下边坡破坏机构模型。

如图1 所示，如果边坡岩土体任意一点的受力状态满足屈服准则时，则边坡岩土体在该点处发生破坏。为了方便后续求解，对模型作出如下假设：假设边坡岩土体是围绕旋转中心F围绕弧形滑动面旋转的刚体，在滑动面上，边坡断面下方的土体是保持不动的，露天采矿爆破振动荷载用K表示，坡顶地面附加荷载为S，在极限状态下的滑动面通过坡趾下方B滑动到点c，形成一条包络线。

1.2 求解外力做功功率

在上文建立的采矿爆破振动作用下边坡破坏机构模型上，对边坡外力做功功率进行求解。对于露天采矿爆破振动荷载作用下的边坡，外力做功功率是由边坡岩土体自身的重力和爆破荷载力引起，根据能量平衡守则，在稳定状态下边坡的外力应该与内力相等，边坡内力由黏聚力和毛细黏聚力组成，其用公式表示如下：

式中：Wd为边坡岩土体自身重力所做的功率；Ws为露天采矿爆破振动荷载所做的功率；Dc为边坡有效毛细黏聚力引起的能量耗散率；Da为边坡毛细黏聚力引起的能量耗散率[5]。其中边坡岩土体自身重力所做的功率为：

式中：γ为边坡岩土体重度；r为边坡岩土体滑动角速度；μ为边坡破坏机构模型上滑动面初始半径。为求边坡上爆破振动荷载所做功率，将爆破振动荷载等效为集中力，则露天采矿爆破振动荷载所做的功率计算为：

式中：U为爆破振动荷载等效集中力；k为均爆破振动荷载等效集中力作用点到边坡岩土体围绕旋转中心F的水平距离[6]。综合以上计算可以求出露天采矿爆破振动过程中边坡外力做功功率。

1.3 内部能量耗散功率求解

由于构建的模型是将边坡破坏旋转机构视作为刚体，因此在露天采矿爆破振动过程中，边坡内部能量耗散只可能发生在滑动面上。上文分析到边坡内部能量耗散是由毛细黏聚力和有效黏聚力引起的，根据图1 可知，边坡滑动面通过边坡坡趾下方，在对边坡岩土体内部能量耗散功率计算时，将滑动面上的土体分成饱和状态下土体和非饱和状态下土体两部分，将饱和状态下的土体根据实际情况划分子土层，土层数量为n，土层厚度为h，将非饱和状态下的土体根据实际情况化分土层数量为m个，土层的厚度为x。因此露天采矿爆破振动过程中边坡岩土体毛细黏聚力用公式表示为：

式中：θ为边坡滑动面与水平地面的夹角；y为边坡岩土摩擦力；α为边坡与地基摩擦角。根据相同计算出有效黏聚力耗散率，由此可以求出露天采矿爆破振动过程中边坡内部能量耗散率：

ψ=Dc+Da（10）

式中：ψ为露天采矿爆破振动过程中边坡内部能量耗散率。

1.4 边坡稳定性极限分析

边坡稳定性极限实质就是露天采矿爆破振动过程中边坡安全系数的上限值，因此在上述计算分析基础上，利用强度折减法求出边坡安全系数的上限值。假设边坡安全系数为L，边坡强度折减率为N，当边坡强度折减率大于1 时，则说明目前边坡处于稳定状态，在露天采矿爆破振动作用下，根据强度折减法则，边坡强度折减率为：

当N取值为1 时，边坡稳定性达到极限状态，将上述公式中边坡重力功率、爆破振动荷载功率、有效黏聚力耗散率以及毛细黏聚力耗散率替换成公式（6）、（7）、（9）中参数，并在公式中增加α、γ、ρ三个未知量，每改变一次公式中未知参数，就会得到一个相应的边坡稳定性极限值。因此将露天采矿爆破振动过程中边坡稳定性极限分析问题转化为数学规划问题，利用最优化方法对公式中未知参数值进行最优求解，从而得到边坡稳定性极限值如下：

式中：Lmin为边坡安全系数L的上限解，即露天采矿爆破振动过程中边坡稳定性极限值。

2 实验论证分析

为了验证露天采矿爆破振动过程中边坡稳定性极限分析方法的可行性，以白云岩矿为实验对象，该露天矿山爆破所使用的炸药为乳化炸药，爆破速度为5500 m/s，炸药密度为1.5 g/cm³，装药直径为45.65 mm，爆破钻孔直径为52.41 mm，最大装药量为0.55 kg。该矿山边坡地质为粉质粘土，强度比较低，稳定性较差，实验对该矿山露天采矿爆破振动过程中边坡稳定性极限进行分析。

实验将该矿区边坡分为8 个坡段，对8 个坡段的稳定性极限进行分析，将实验中数据进行记录，利用OUSF 软件将两种方法分析结果与实际情况进行差值计算，求出两种方法分析偏差，将其作为两种方法对比分析指标，验证此次提出的分析思路相比较传统方法是否有所优化。实验结果见表1。

表1 两种方法偏差对比

从表中数据看出，设计方法分析偏差比较小，平均值为0.001，分析值与实际值基本相等，设计的分析方法精度较高；而传统方法分析偏差最大值为0.068，平均偏差为0.038，远远高于设计方法。

3 结语

本文结合摩尔-库伦屈服理论和强度折减法，提出一个新的边坡稳定性极限分析思路，并通过实验论证了该思路的可行性与可靠性。此次研究实现了露天采矿爆破振动过程中边坡稳定性极限分析方法优化与创新，有效提高了分析精度，能够为露天采矿施工安全防护以及边坡滑坡事故预防提供准确的数据依据。