高耸烟囱结构调谐质量惯容阻尼器(TMDI)风振控制方法及效果研究

苏 宁，彭士涛，洪宁宁

(交通运输部天津水运工程科学研究所，天津 300456)

高耸烟囱结构对风荷载作用极为敏感，尤其是横风向涡激共振会对结构安全造成不利影响，其风振控制是结构抗风优化设计中的重点和难点。调谐质量惯容阻尼器(tuned mass damper inerter，TMDI)是一种基于惯容器的新型的动力吸振装置。一种常见的齿轮齿条式惯容器示意图如图1 所示，惯容器提供的阻尼力fb与两个连接端相对加速度u¨1-u¨2成正比。比例系数b称为惯容系数，其取值仅与齿轮和飞轮的机械参数有关，通过齿轮和飞轮的合理选型，惯容器能够自身重量成百上千倍的质量惯性效应[1]，充分利用该效应有助于实现动力吸振器的轻量化设计[2-3]，近年来得到广泛关注。

DEN HARTOG 基于不动点理论[4]，给出了传统的调谐质量阻尼器(TMD)的参数优化及振动控制性能经验公式。后期学者们就主结构阻尼比、激励荷载形式等方面对上述理论进行了完善[5-6]，形成了完整系统的结构振动控制理论体系。另有学者们，在此基础上结合等效线性化方法，提出了调谐液柱阻尼器(TLCD)[7-8]、非线性能量阱(NES)[9-11]等非线性吸振器的分析体系。

TMDI 引入惯容器后，使得运动方程更为复杂，学者们对相应的参数优化及控制效率评估方法进行了讨论[12-13]，但这些研究都是基于惯容器与地面相连进行推导的，又称为GTMDI(grounded TMDI)。而对于高层或高耸结构，惯容器接地难以在工程中实现，一些学者将GTMDI 与基底隔震系统相结合[14]，使其更具实际应用价值。在应用层面，TMDI 系统更容易安装在高层结构的层间[15-16]，或在连体高层的振动控制中发挥作用[17-18]。此外，还应用于大跨度桥梁结构的断面间[19]，以控制涡激共振的不利影响。

研究表明，惯容器的连接位置不仅影响其在工程中的实施难度，而且对TMDI 的控制效果影响较大，且仅在一定范围内，效果明显优于TMD[20]，但文中尚未针对惯容器的位置的影响进行参数化分析。后有学者建立了TMDI 控制广义单自由度振动的悬臂柱振动响应的运动方程，讨论了截面变化对控制效果的影响[21]，说明TMDI 的控制效果与惯容器连接位置处的振型关系密切，但文中未给出相关的经验公式供设计参考。

本文将高耸烟囱简化为广义单自由度结构，基于风荷载频谱的滤波表示，推导了TMDI 控制下结构风振响应的解析解。在此基础上，对TMDI最优设计参数进行了参数化分析，总结了相应的经验公式供设计参考。此外，通过对比TMDI 与TMD的风振响应控制效果，给出了惯容器起增强控制效果的判别准则，以及TMDI 的等效TMD 质量比计算公式，以指导动力吸振器的轻量化设计。最后通过对某270 m 高混凝土烟囱风洞试验数据进行TMDI 风振控制算例分析，验证了理论分析的有效性，并探讨了TMDI 对高耸烟囱的风振响应控制效果。

假设圆柱形烟囱内、外半径沿高度z的变化分别为Ri(z)和Ro(z)，将高耸烟囱结构分析模型假设为连续质量的振动体系，质量、刚度沿高度分布m(z)、EI(z)分别为：

1 理论推导

1.1 运动方程

式中：ρs、E分别为烟囱结构的材料密度和弹性模量；me(z)为恒活荷载等效质量代表值沿高度的分布。

将无控的烟囱结构(不含TMDI)进一步简化为广义单自由度振动体系(图2)。沿高度变化的振动位移u(z,t)解耦表示为广义位移响应x(t)与归一化振型函数Φ(z)的乘积：

其中，Φ(H) = 1，则x(t)在数值上等同于顶点位移u(H,t)。结构的广义质量M、广义刚度K分别表示为：

当采用TMDI 进行振动控制时，TMDI 的质量为m，刚度为k，阻尼为c，惯容系数为b，惯容器连接位置(高度)χ。惯容器的连接位置(高度)χ与振动控制效果具有很强关联。一般来说，χ越小，惯容器的两端距离越大，两端相对加速度越大，振动控制效果越好。同时，χ的减小会增加惯容器的安装难度。因此，χ的取值需要权衡控制效果与可实施性。在理论推导中，定义惯容器位置参数为其连接位置处的振型值，即φ= Φ(χ)，这里，φ随χ的单调增减。

TMDI 的振动频率ωd和阻尼比ζd分别定义为：

定义TMDI 调制比参数，质量比μ=m/M，惯质比β =b/M，频率比ν=ωd/ωs。根据虚功原理[22]，可将体系运动方程组表示为：

1.2 振动响应分析

其中，Hx(ω)为烟囱主结构位移响应频响函数的分子多项式，该多项式为偶次多项式，其偶次项系数为θj(j= 0, 1, 2)。

TMDI 的响应控制比J0定义为控制后的响应标准差与无控响应标准差之比，响应控制率η 定义为控制后响应X减小量占无控响应X0的百分比，当以脉动响应标准差(均方根)计算响应控制率时，η = 1 -J0。

由式(14)、式(21)的频域积分可得结构在无控和控制状态下的响应，当假设风荷载激励假设为强度为δ 的白噪声时，即Sξ(ω) = δ，根据闭路积分定理[22]可得响应的解析表达式如下：

式中，N0和Nx为控制响应的分子和分母表达式。则白噪声激励下响应控制比为：

将广义风荷载频谱表示为如式(31)所示的白噪声滤波的形式，则可求得式(14)、式(21)的解析表达式，能够更为便捷高效地分析各参数对响应及控制效果的影响[23]。

1.3 风荷载谱的滤波表示

式中： Λa(ϖ)、δa分别为顺风向风荷载谱Sξa(ω)的滤波多项式和归一化强度；ωa表示顺风向无量纲风荷载谱峰值所对应的圆频率。图3(a)给出了横风向无量纲广义风荷载谱风洞试验数据和相关模型的对比，可见，采用该滤波模型总体能够较好地反映顺风向风荷载谱在高频段的衰减趋势。

对于横风向风荷载，由于漩涡脱落引起的涡激振动，使得能量在斯托罗哈频率附近集中，无量纲风荷载谱曲线具有较为显著的凸起，其滤波多项式可由二次函数来表示：

根据闭路积分定理[22]可得，无控状态下的顺风向及横风向风振响应为：

值得说明的是，采用式(35)计算横风向响应时，阻尼比ζT= ζs+ ζa为考虑气动阻尼ζa的总阻尼比。

横风向风振响应σxa按式(40)～式(43)计算。式中，Dc0和Dc1为横风向响应的分母和分子行列式，分别由式(41)、式(42)计算；κcj为横风向响应滤波多项式Kc(ϖ)=Λc(ϖ)·Γ(ϖ)的j次项系数(j=0, 1, 2, 3, 4, 5, 6)，由式(41)确定。其中， γ′j为式(20)中的γj(j= 1, 2, 3)，但结构阻尼比ζs由总阻尼比ζT=ζs+ ζa替代。

顺风向及横风向风振响应的控制比不仅随阻尼器参数变化，还随着风荷载频率与结构频率之比(ωma/ωs、ωmc/ωs)变化，一般地，当风荷载频率与结构频率接近产生共振时，响应控制效果最好。定义顺风向、横风向的共振响应控制比Ja、Jc来描述TMDI 对顺风向及横风向响应的控制效果。

图4 给出了几个典型工况下白噪声激励下的响应控制比Jw(由式(30)计算得到)、顺风向及横风向共振控制比Ja、Jc(分别由式(44)、式(45)计算得到)随TMDI 频率比ν和阻尼比ζd变化的等值线图。由图4 可以看出，Jw、Ja、Jc在(ν，ζd)平面上存在一个极小值点，即理论最优参数。

2 TMDI 参数优化

2.1 参数寻优方法

TMDI 的参数优化指根据质量、惯容参数(μ，β，φ)，确 定 最 优 的 频 率 比 和 阻 尼 比(νopt，ζdopt)使得响应控制效果最优，也就是，在特定的参数(μ，β，φ)下，寻找J0(或Jw、Ja、Jc)曲面的最小值点。第1 节给出了J0的解析计算方法，可大幅度提高计算效率和精度。由图3 分析可知，给定参数(μ，β，φ)时，一般存在唯一的理论最优参数(νopt，ζdopt)可由下式得到：

式中：J0也可以用Jw、Ja、Jc替代；Jopt为最优参数(νopt，ζdopt)下的响应控制比。

理论上可以利用式(30)得到的白噪声激励下的Jw解析表达式推得最优参数(νopt，ζdopt)随(μ，β，φ)变化的表达式。但由于导函数表达形式过于复杂，无法得到解析解。因此，本文采用数值优化方法—共轭梯度法，在不同的(μ，β，φ)条件下对(νopt，ζdopt)进行寻优。利用基于Den Hartog的不动点理论得到的GTMDI 最优解(式(47))[16]寻优迭代的初值进行计算。

研究表明，结构阻尼比ζs对最优参数(νopt，ζdopt)结果影响较小[10]，因此在参数分析时，仅考虑ζs= 1%，分析参数(μ，β，φ)的变化范围为：

1)μ= 10^[-3∶0.1∶-1] (共41 种取值)；

2) β = [0, 0.01, 0.02, 0.05, 0.1: 0.1: 1.0] (共14 种取值)；

3)φ= [0: 0.1: 0.5, 0.60: 0.05: 0.80, 0.82: 0.02:1.00] (共21 种取值)。

对白噪声、顺风向、横风向3 种激励模式下的控制比Jw、Ja、Jc进行分析，共计36 162 个计算工况。

图5 给出了μ= 1%情况下，三种激励模式最优控制参数(νopt，ζdopt)和最优控制比Jopt随惯容器参数(β，φ)的变化。总体看来，随着惯质比β 增大、惯容器连接位置降低(φ减小)最优频率比νopt降低，最优阻尼比ζdopt增大，这种变化趋势随着φ增大而减弱。惯容器连接位置降低(φ减小)，最优控制比Jopt减小，控制效果增强。当φ=0 时，GTMDI 最优控制比随惯质比β 增大而减小。而当φ= 1 时，随着惯质比β 增大，Jopt呈现增大趋势。虽然三种激励模式下，虽然最优控制参数(νopt，ζdopt)存在一些差异，但Jopt对激励模式不敏感。

2.2 最优参数经验公式

根据上述参数分析结果，总结出TMDI 最优控制参数(νopt，ζdopt)关于质量、惯容参数(μ，β，φ)的经验公式如下：

图5(a)、图5(b)给出了最优控制参数(νopt,ζdopt)经验公式和分析结果的对比，可以发现，经验公式和分析结果趋势一致，但局部存在一定差异。将采用经验公式得到的最优控制参数下的最优控制比与分析结果的对比，如图6 所示。可以发现，即便经验公式估计最优控制参数造成了一定误差，但对最优控制比结果影响不大。这可能是由于最优控制参数(νopt, ζdopt)附近的控制比曲面J0(ν, ζd)形状较为平坦，从一定程度上削弱了最优控制比Jopt结果对最优控制参数(νopt, ζdopt)误差的敏感性。对Jopt的误差进一步统计分析发现，97%以上的Jopt结果误差不超过10%，说明该经验公式在的误差是工程中可接受的，可以用于估算TMDI 的最优参数。optdoptopt

特别是，当φ= 0，式(48)变化为GTMDI 优化参数的取值，见式(49)；进一步，当β = 0 时，式(48)变化为TMD 最优参数取值，见式(50)。

3 最优风振控制效果分析

3.1 与TMD 最优控制效果的比较

TMDI 研制的初衷之一是通过惯容器增强TMD 的振动控制效果。通过上述研究发现，惯容器的连接位置对TMDI 的振动控制效果影响至关重要。由图5(c)可知，惯容器接地时(φ= 0，GTMDI)的控制效果最优。而对比图4(a)和图4(d)发现，当φ= 1 时，其控制效果可能不如相同质量比下的TMD。为比较相同质量比μ下TMDI 与TMD 的控制效果，定义惯容器影响系数R为TMDI 与TMD的响应控制比之比，即：

当R＞ 1 时，TMDI 的控制效果不如TMD；当R≤ 1 时，惯容器起到增强振动控制的效果，称为惯容增强区。R值越小，增强效果越显著。

图7 给出了2.1 节参数分析中μ= 1%时R随惯容器参数(β，φ)的变化等值线图。可以发现，惯容增强区内(R≤ 1)，随着惯质比β 增大、惯容器连接位置降低(φ减小)，振动控制增强效果越显著。

图8 给出了μ= 0.1%、1%和10%时的惯容增强区边界线。可以发现，随着质量比增大，惯容增强区域的边界向着惯质比β 增大、惯容器连接位置降低(φ减小)的方向移动。为进一步定量给出惯容增强区的条件，在2.1 节参数分析的基础上对结构阻尼比ζs= 0.1%、10%进行了补充分析。将结果绘制在以R值为纵轴，β·(1 -φ)2/μ为横轴的坐标图上，如图9 所示。从图中可以看出，一般地，当β·(1 -φ)2/μ≥ 1时，有R≤ 1。而R＞ 1 的情况大多出现在β·(1 -φ)2/μ＜ 1 时。因此，在工程上可以偏于保守地将惯容器起增强作用的判定条件表示为：

为验证上述准则的有效性，对其进行统计假设检验。分别绘制R＞ 1 和R＜ 1 时，判别参数β·(1 -φ)2/μ的概率分布图，如图10 所示。由统计分析可得，判别式(52)的I 类统计错误(即在β·(1 -φ)2/μ＜1 时R＜ 1)概率约为4.85%，但II 类统计错误(即在β·(1 -φ)2/μ＞1 时R＞ 1)的概率低于10-4，说明判别式(52)的去伪率较高，具有较强的统计检验效能。

3.2 等效TMD 质量比

TMDI 的一个重要作用是通过惯容器提供足够的质量惯性效应以实现动力吸振器的轻量化设计。本节以最优控制比为等效目标，重点给出惯容增强区内，TMDI 的等效TMD 质量比，从而指导动力吸振装置的轻量化设计。

其中：μe为TMDI 的等效质量比，当TMD 时(β =0)，取为μ；GTMDI 时(φ= 0)，取为μ+ β；在惯容增强区的TMDI 时(β(1 -φ)2/μ≥ 1)，取为μ+β(1 -φ)2。

则惯容器影响系数R进一步表示为：

将式(57)结果与3.1 节的惯容影响系数R分析结果进行对比，如图12 所示。从图中可以发现，经验公式在惯容增强区(β(1 -φ)2/μ≥ 1)范围内误差在10%以内，验证了等效质量比的有效性。而当β(1 -φ)2/μ＜ 1 时，由于惯容器无增强控制效果，不推荐在工程中使用。

4 算例分析

本文以某H= 270 m 高混凝土烟囱为例，进行TMDI 风振控制算例分析。图13 给出了该混凝土烟囱的截面尺寸(内外半径)随高度的变化，烟囱的平均外直径D= 25.34 m。采用梁单元模拟烟囱该烟囱沿高度的刚度变化，建立多自由度有限元分析模型，经过模态分析得到烟囱的前三阶自振圆频率和振型如图13 所示，可得烟囱横风向涡激共振的临界风速为UCr= 49.4 m/s。

为确定该烟囱风荷载及风振响应，对其进行了刚性模型测压风洞试验及气弹模型测振风洞试验[29]，风洞试验模拟美国规范ASCE 7-16[30]中的C 类风场，在交通运输部天津水运工程科学研究所大气边界层风洞实验室中进行。通过刚性模型测压风洞试验数据分析得到结构顺风向及横风向的广义风荷载频谱见图3，通过气弹模型风洞试验得到烟囱风振响应时程，对横风向响应进行随机减量法分析，得到自由振动衰减曲线，进而对自由衰减曲线的包络线进行参数拟合，得到烟囱结构横风向气动阻尼及总阻尼比，如图14 所示。

对于风振控制，以质量比μ= 1%的TMD 为基准，TMDI 采用惯质比β = 20%的惯容器，连接参数取φ= 0.9、0.75、0.5 和0.0，分别表示惯容增强区外、惯容增强区边界附近、惯容增强区内、GTMDI 4 种情况。采用本文给出的经验公式计算最优的频率比和阻尼比(νopt, ζdopt)和等效质量比μe，风振控制计算工况阻尼器详细参数见表1。

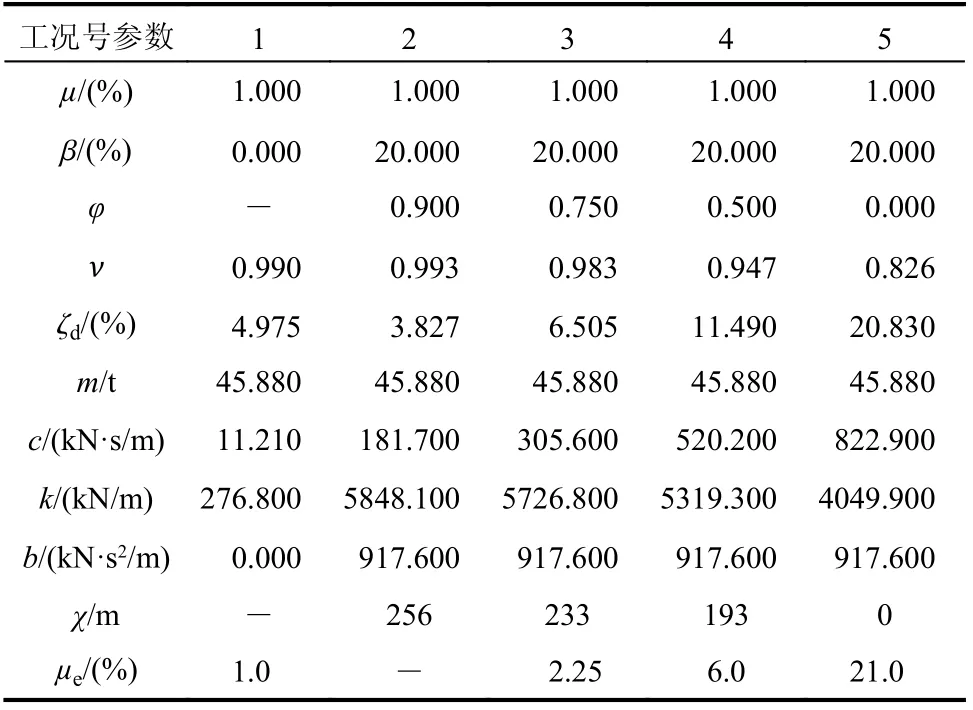
表1 风振控制计算工况阻尼器详细参数Table 1 Detailed damper parameters of wind-induced vibration control cases

风振响应计算分析分别采用多自由度结构的动力响应时程分析法以及本文提出的滤波表示解析计算方法(式(36)、式(40))。

表2 给出了典型风速下(锁定区前、临界风速附近、锁定区外)的风振响应计算结果对比。可以看出风速较低时，由于响应本身较小，计算存在相对误差角度，随着响应变大，计算误差减小，在临界风速附近和锁定区外本文方法和传统时程分析相比误差在±5%以内，说明本文解析方法对单自由度振动为主的高耸烟囱结构具有较强的适用性。虽然表2 表明，传统时域分析结果更接近气弹试验结果，但采用本文的解析方法计算，无需复杂迭代计算，更为快捷，给出的解析公式更便于规范化表达，同时也适用于项目初步设计阶段的快速估算。

表2 典型风速下风振响应计算结果及误差Table 2 Results and errors of wind-induced responses under typical wind speed cases

图16 给出了典型控制工况3、4 下烟囱在临界风速附近(U/UCr= 1.17)横风向共振响应时程的分析结果，图中对比了TMDI 和等效TMD 的响应时程。从图中可以发现二者吻合较好，进一步验证了本文等效TMD 质量比的有效性。根据ACI307-08 规范[31]综合考虑顺风向极值响应Xa、横风向组合响应Xc。

其中：x¯a为顺风向响应的均值；ga、gc分别为顺风向和横风向响应的峰值因子；X(U)为风速U时的最不利响应。由于横风向涡激共振受气动阻尼的影响，X(U)并不一定随U增大而增大，因此下设计风速Ud下的最不利响应Xd取U≤Ud的包络值。并利用最不利响应Xd计算风振响应控制率η，分别见图17、图18。

最不利响应Xd表征了在设计风速Ud下等效静风荷载的取值，控制率η 显示了采用TMDI 后降低设计风荷载的百分比。由图18 可见，当设计风速与临界风速相接近时，响应控制率达到最大。采用控制工况3 时，设计风荷载可降低越35%；控制工况4 可降低设计风荷载约47%；GTMDI 可降低约59%，但在工程中难以实施。当设计风速超出涡激共振锁定区(Ud＞ 2UCr)时，采用控制工况3 和工况4 分别可降低设计风荷载约26%和33%以上。

5 结论

本文从基本运动方程出发，基于滤波表示法推导了广义单自由度高耸烟囱结构TMDI 风振响应控制效率解析表达式，通过参数分析，得到了TMDI 最优参数、最优控制比及等效TMD 质量比的经验公式。并以某270 m 高混凝土烟囱为例验证了理论推导及经验公式的有效性，探讨了TMDI对其风振响应的控制效果，主要结论如下：

(1) 高耸结构风振响应分析时，可将顺风向和横风向的风荷载谱表示为滤波形式，滤波多项式分别为一次和二次多项式，对于一阶模态主导的结构，该方法得到的解析解与传统时域分析结果较吻合。

(2) 采用本文给出的TMDI 最优控制参数(νopt，ζdopt)关于质量、惯容参数(μ，β，φ)的经验公式计算的最优响应控制比Jopt误差在工程接受范围内。

(3) 当β·(1 -φ)2/μ≥ 1 时，TMDI 的控制效果优于相同质量比μ下的TMD，说明此时惯容器起到增强控制效果的作用，定义为惯容增强区。统计假设检验表明，该准则具有较强的统计检验效能。

(4) 在惯容增强区内(β·(1 -φ)2/μ≥ 1)，TMDI可等效为质量比为μe的TMD，其中，等效质量比μe= β·(1 -φ)2。

(5) 高耸烟囱算例分析结果表明，TMDI 对横风向风振响应控制效果显著。当设计风速与临界风速相接近时，响应控制率最大，可降低设计风荷载45%以上；当设计风速超出涡激共振锁定区(Ud＞ 2UCr)时，TMDI 可降低设计风荷载30%以上。