基于MLP神经网络的盾构推进速度预测研究
2022-11-05周奇才熊肖磊
赵 炯 马 超 周奇才 熊肖磊
同济大学机械与能源工程学院 上海 201804
0 引言
为了减少隧道施工安全问题,发展智能化盾构施工技术,现在隧道施工盾构机都往智能化方向发展[1],包括智能掘进和智能化管片拼装。然而,目前这方面还缺乏系统的、完善的掘进适应性决策体系和理论基础[2],依据不同环境和不同地质条件,盾构机需要作出不同的参数调整。传统方法是靠人工视情况调整各参数,使其在不同环境下能正常工作,难免会有意外情况,虽问题不大但对施工过程会有影响。所以,对智能化盾构的研究不仅会对隧道工程的发展有很大的促进作用[3],而且也能进一步提高隧道施工的安全性,保障施工人员的安全和提高工程效率[4]。
针对以上问题,利用现有的一系列成熟数据处理和机器学习方法将盾构的历史数据进行整合和处理,将其运用到合理的机器学习算法中,得出各类传感器数据与推进速度之间的模型。将实时的传感器数据放入此模型中,从而得出此时对应的推进速度。
1 MLP神经网络模型
神经网络与人类的神经网络相似,是科学家从人类身上得到启发而建立的一种学习模型。它由一个个单独的神经元组成,每个神经元接收其上一层神经元所发送的信息,经过多个神经元的传递给出最终的信息,也就是所需要的数据值[5]。
如图1所示,多层感知器的基本结构主要由输入层、隐藏层和输出层等组成。隐藏层可以有多个层次,输入层和输出层一般都只有一层,输入层不同的神经元代表的是不同的特征,输出层是最终输出的数据,可以有多个,这里只是针对本次的研究只画出一个神经元。
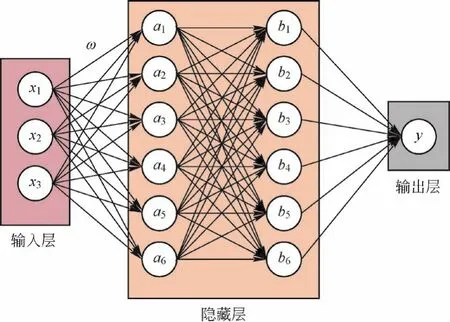
图1 多层感知器(MLP)的基本构成
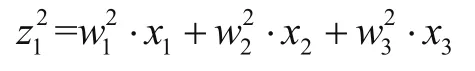
对应下一层的取值为
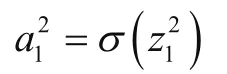
在上述表达式中,上角标表示的是计算的下一层层数,σ函数在神经网络中称为激活函数,确定激活函数也是神经网络的核心[6]。在隐藏层中,每个神经元都存在一个激活函数,数据的流向逐层传递,每一层处理的数据都是上一层传递的数据,故确定隐藏层数量和激活函数在神经网络中尤为重要。本文所选输出层的激活函数是Adam函数,隐藏层一般有3种激活函数可以选择,即非线性矫正函(Relu)、双曲正切处理函数(Tanh)和Sigmod函数(Logistic),本文选择的激活函数是Tanh函数,可表示为
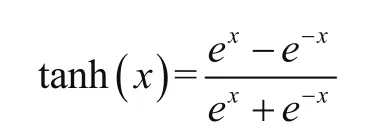
神经网络其实是一个黑盒模型,对使用者来说可见的就是输入层,输出层,隐藏层对应的层数、神经元数量和激活函数。输入层对应的是输入的特征值,输出层是要得到的数据集。所以,神经网络中最重要的就是确定隐藏层的层数、每层的神经元数量、对应的激活函数。当然,这些数值要依据具体数据进行计算,多次调整对应的参数得到最好的结果。
2 数据处理
本文所使用的每台盾构机数据字段大约有400个,数据大约有3万条左右,在此只选取1台盾构机的数据进行计算。
2.1 数据初筛
每个盾构数据表都有一张对应的参数说明,通过每一张盾构表的参数说明即可得知很多字段是开关量。不仅如此,还有很多字段的数值一直为常量值,分析这些数据字段与推进速度无直接关系,进行数据处理时可直接删除,经过这一步的数据筛选留下44个字段。
2.2 零值和异常值处理
本文主要研究盾构机推进时的推进速度,所以除去管片拼装时产生的数据,即将推进速度小于等于0的数据行删除。
2.3 数据导出
按照前2步数据筛选条件将数据进行第1步筛选,然后数据通过数据库导出并保存为CSV文件,使用Python的Pandas模块对这个文件进行读取,之后使用Describe方法形成一个数据表格,如表1所示。
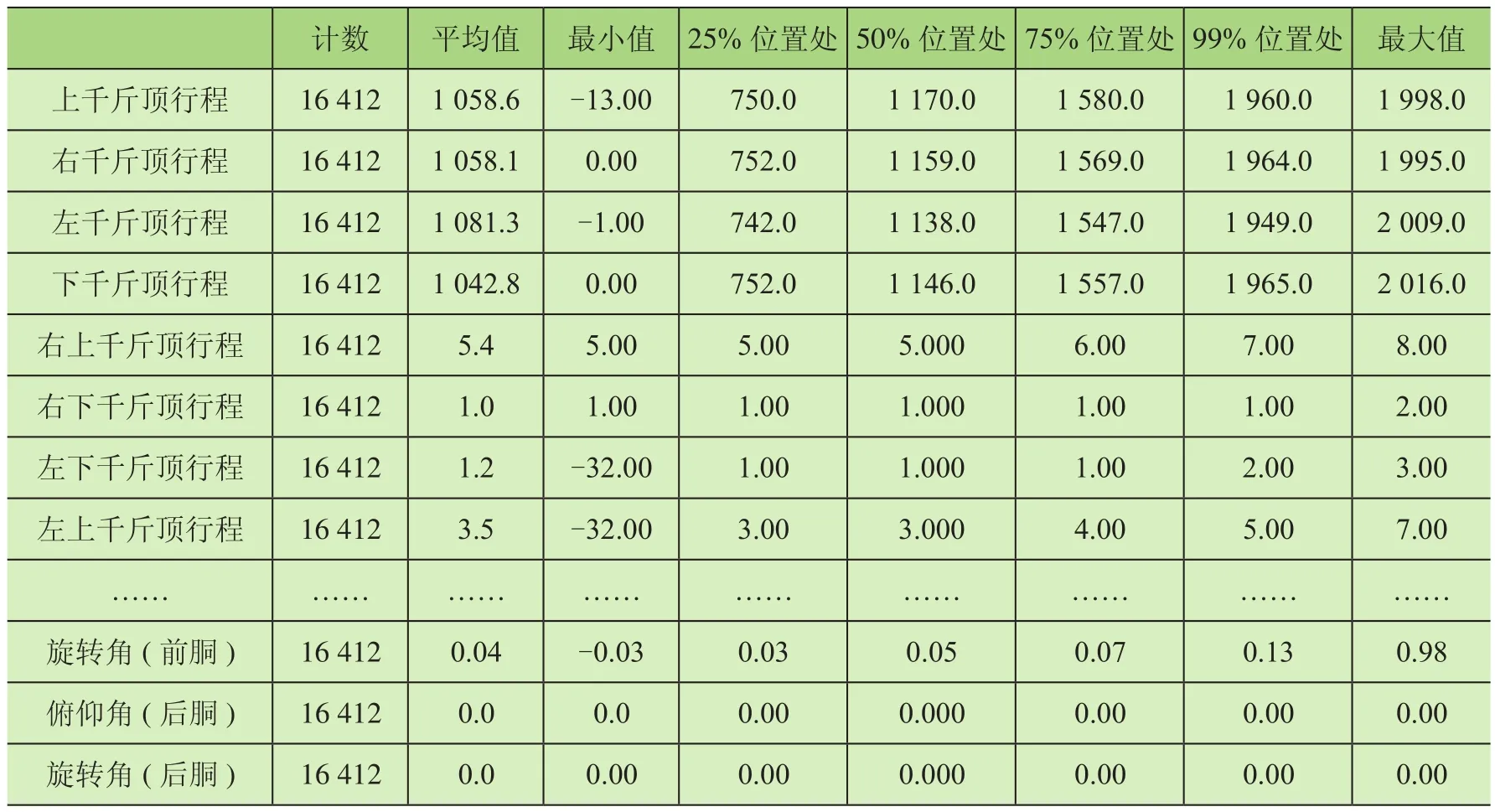
表1 筛选条件实际数据值
由表1可知,目前还有很多字段是不可用的,其数据有异常值,表中25%、50%、77%、99%等是将该列数据进行排序之后处于相对应位置的值。分析可能出现这些异常值的原因是在实际的工程环境中网络通信异常或关键的传感器出现问题,亦有可能某些字段只是列出来而并无在实际过程中的应用。删除之后再进行统计化的查看,截取部分统计数据如表2所示(此处截取出的数据表示在上一步处理完成之后还有异常的部分数据)。
1.1.5 文献排除标准 无法获得全文,无有效数据提取,同一作者或同一研究团队重复发表,孕妇合并严重并发症,非随机对照研究,回顾性研究,综述及动物实验,非英文或中文的文献。
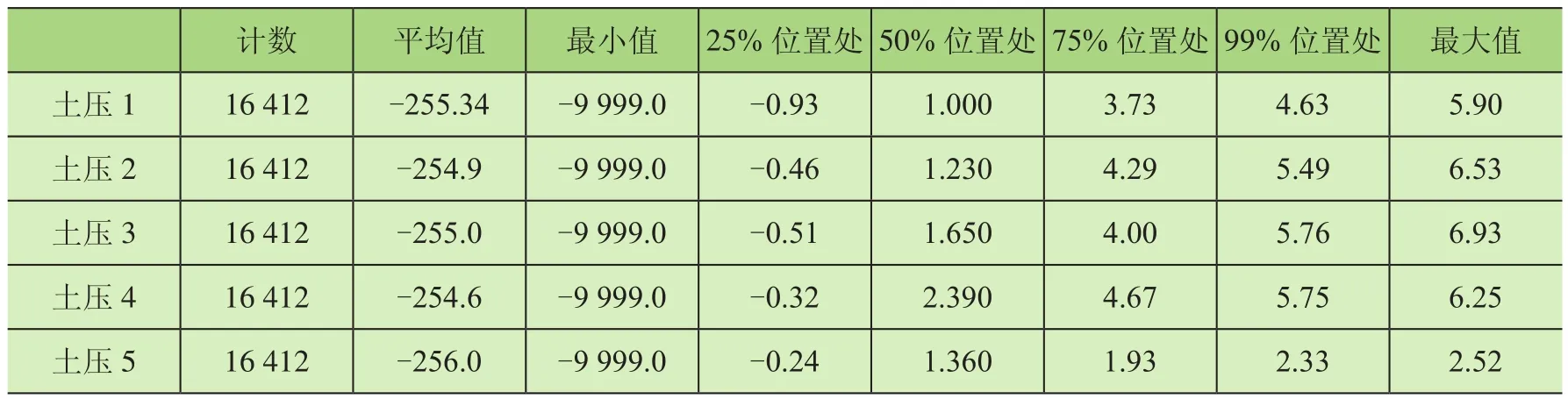
表2 土压异常值
由表2可知,土压最小值多为-9 999,而在盾构运行过程中土压不会为负值,所以在此进行下一步操作,将土压为负的行数据删除。完成之后最后再查看一次数据,此时有部分数据受到影响,这些数据包括俯仰角、侧滚角、方位角、刀盘液压泵出口压力、1号仿形刀行程、2号仿形刀行程等。在删除土压为负值的行后,这部分数据均为0,对此后的数据计算无关键作用,在此处对其进行删除。
2.4 提取目标值
经过上述处理后,将目标数值列提取出来单独作为一张表,然后在原数据上推进速度列删除。
2.5 归一化
使用Sklearn.Preprocessong中的MinMaxScaler模块对剩余的数据进行数据归一化。数据归一化之后,需要对每一列按照之前的命名顺序进行命名,在此加上数据对应的每一列的名字以便后面的观察。
2.6 特征提取
对数据进行卡方检验对之前处理后的数据进行打分,提取合适的数据特征。使用Sklearn.Feature_Selection中的SelectKBest和Chi2模块进行数据的卡方检验,在此使用的数据是之前提取的推进速度,也就是标签值;另一个是进行归一化处理后的数据集。设置30%为测试集,70%为训练集,进行训练打分之后的特征如表3所示。
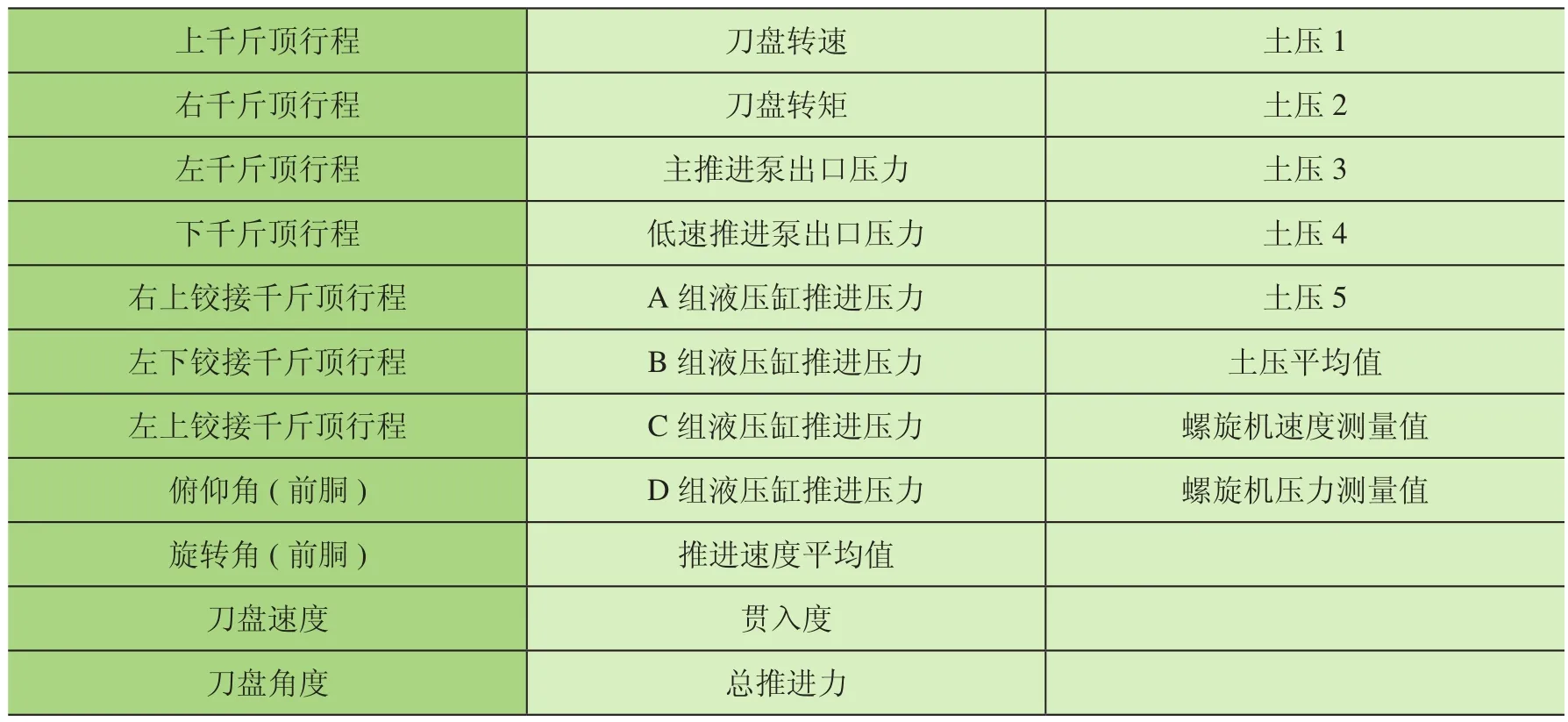
表3 卡方计算结果
表3所示为最终选定的特征值,随后在推进速度预测中将用到传感器的参数对应的数据。
3 MLP神经网络回归算法
在使用神经网络前,先对数据进行标准化操作,在此使用的数据不是在卡方时归一化的数据,而是在归一化之前的原始数据。标准化数据完成后使用Sklearn Model_Selection中的Train_Test_Split模块对其进行训练集和测试集的划分。在标签值使用前得到推进速度,然后设置30%的数据为测试集,70%的数据为训练集。对数据和标签值进行数据划分。当数据集划分完成,即使用Sklearn.Neurak_Network中的MLPRegressor模块进行神经网络回归算法的运算。在计算中,选用4层隐藏层,使用这些参数的原因是通过多次的算法运算和验证,数据在这些神经元下计算能得到较好的计算结果。设置计算的最大迭代次数为40 000次,在此处一定要设置最大迭代次数,如果使用默认值迭代将有可能出现迭代次数不够无法得到最后结果。在每个神经元中都需要一个激活函数,本次计算中选用Tanh,如果未激活函数,隐藏层中的数据关系将是线性的,隐藏层没有起任何作用,所以应使用一个非线性的激活函数。梯度下降选择Adam,其他参数设置为默认。
4 运算结果
在MLP神经网络中,评价回归模型有平均绝对误差、中值绝对误差、可解释方差值等评价指标,对应的最优值和其在Sklearn中对应的函数如表4所示。

表4 各种评价指标
经过计算后,得到对应的值为 :平均绝对误差1.074,中值绝对误差0.431,可解释方差值0.996。最后使用测试集的值代入模型中得出对应的推进速度预测值,再将预测值和实际数据在同一副图上表示出来,如图2所示。

图2 预测值与实际数值结果图
在图2中,红色表示实际值,蓝色表示对应的预测值。每一个数值都有一个对应的自增标签,本次实验的数据中所用的数据一共有8 000多条,将其中的30%用作实际的目标值,即有2 000余条数据。横坐标表示的是从0~2 000条数据对应的标签值,2组数据中对应数据的标签值是一样的,故用标签值作为横坐标。纵坐标是预测值和真实值得具体数值,但由于数据比较多,在一张图中无法准确表达,所以在这里选了4个区段的值每10个数据为一个区域,红色线是目标值,蓝色线是预测值。在图2a中,基本每个点数据都是相同的,但仍有差值,而图上点的坐标跨度较大,无法明显看出。在图2b、图2c中,可以看出几个点有很明显的差异,但相差不多,在可接受范围内。
由图2可知,大部分的值和真实值相接近。尽管在有的数据值上会有差异,但这些差异都保持在2左右。在实际运行时,这些差值在可接受范围之内的,本次模型的研究总体而言符合预期的要求。
