化妆品功效评价统计分析中的差异关系及R语言实现

王福鑫 赵志龙 矫筱蔓

【关键词】R语言；化妆品功效；统计分析

2021 年4 月，国家药监局发布的《化妆品功效宣称评价规范》为化妆品及原料提供了功效性评价方法的要求和规范。化妆品功效评价的研究采用哪种统计分析工具，对研究结论的准确性、科学性把控尤为重要。R语言作为一门现代统计分析工具，不仅在统计方面有很强大的功能，同时也具有极强的可视化功能。R语言常用于生物、医学等相关领域。化妆品研究领域中鲜有利用R语言进行统计分析的报道。在化妆品功效评价研究中，R语言可更好地帮助研究人员设计试验方案，进行数据总结和分析。本文着眼于用R语言实现化妆品功效评价数据处理中常见的差异关系分析，并举例提供参考代码。

1 正态分布和方差齐性

正态分布是统计学中最重要、最常见的分布之一。较常用的差异关系分析如t 检验和方差分析均需要对数据分布情况是否为正态分布和方差齐性进行验证。

对于数据的正态性检验主要可以通过Q-Q 图（见图1）、Pearson 拟合优度卡方检验、K-S拟合优度检验和S-W检验等。在R 语言中，使用chisq.test（）函数完成Pearson 拟合优度卡方检验，使用ks.test（）函数来进行K-S 检验，使用shapiro.test（）函数来完成S-W正态性检验。

如果样本数在50 以下选择S-W检验，样本数在50 以上选择K-S 检验。Q-Q图可最直观地显示样本数据是否符合正态性分布。例如，有100 名受试者参加功效评价试验，拟对其进行数据正态性检验，用rnorm 模拟生成随机数作为样本，利用基础包中的函数分析，程序及结果如下：

> set.seed（12）

> nordata<-rnorm（100，mean=2，sd=5）

> par（pty="s"）

> qqnorm（nordata，pch=1， frame=FALSE）

> qqline（nordata，col="steelblue"，lwd=2）

進一步检验数据是否服从标准正态分布可使用ks.test（）

函数，程序及结果如下：

> ks.test（x=nordata，"pnorm"）

## One-sample Kolmogorov-Smirnov test

## data：nordata

## D=0.443，p-value<2.2e-16

## alternative hypothesis：two-sided

从输出的p-value<2.2e-16 来看，说明nordata 不服从标准正态分布（随机数设置为平均值为2，sd 为5）。

方差齐性检验是检验不同样本的总体方差是否相同的一种方法。常用的检验方法有F 检验、Bartlet 检验和Levene 检验。建议首选使用Levene 进行样本齐性检验，因其更稳健且不依赖总体分布情况，还可用于多组样本。例如，对3 个实验组受试者进行方差齐性检验（t1 对照组、t2 阳性组和t3 试验组均以随机数为例做样本），使用car 包中的leveneTest（）函数进行Levene检验，程序和结果如下：

> library（car）

> testdata<-data.frame（x=c（t1，t2，t3））

> group1=c（rep（c“（ A”“， B”“， C”），c（100，100，100））））

> leveneTest（x～group1，data=testdata）

## Levene's Test for Homogeneity of Variance （center=

median）

## Df F value Pr（>F）

## group 2 0.7591 0.469

## 297

使用小提琴图（利用ggplot2 包）将t1，t2 和t3 组结果进行可视化，观察三组样本的离散程度，对比数据的方差大小。图2 中A、B、C分别对应t1、t2 和t3 组，由小提琴图可以发现，虽然t1 组、t2 组和t3 组数值范围不同，但离散成果很相近，这也与使用方差齐性检验得到的结果一致。

2 t检验

在研究中，我们常关注组间差异的比较问题。例如，使用某种具有特定功效的化妆品和之前使用某种化妆品比较，使用效果是否有明显改善。在样本整体符合正态分布且具有方差齐性的条件下，独立样本t 检验可以很好地实现分析目的。t 检验主要分为三种，分别是单样本t 检验、配对样本t 检验、独立样本t 检验。它们本质上都是对比均值，但在不同的分析研究环境中应选择不同的t 检验。单样本t 检验主要用于比较一组数据与一个特定数值之间的差异情况，一般可以用于分析整体的态度倾向。独立样本t 检验用于分析定类数据与定量数据之间的差异情况。例如，在两种背景下（使用和不使用化妆品），比较女性消费者的皮肤弹性是否有明显的差异性。通过两组数据的对比分析，判断该化妆品是否会影响皮肤弹性水平。以数据集flex 为例（该数据集并非研究结果，请自行设置数据集），程序和结果如下：

> t.test（flexindex～use，var.equal=TRUE，data=flex）

## Two Sample t-test

## data：flexindex by use

## t=2.6529，df=187，p-value=0.008667

## alternative hypothesis： true difference in means between

group 0 and group 1 is not equal to 0

## 95 percent confidence interval：

## 72.75612 494.79735

## sample estimates：

## mean in group 0 mean in group 1

## 3055.696 2771.919

參数var.equal 用于设置方差是否齐性，默认为FALSE（不齐）。由上面方差齐性检验的结论，设置为TRUE。结果表明皮肤弹性水平在使用化妆品和不使用化妆品的女性之间有显著差异（p 值为0.008667）。

配对样本t 检验，用于分析配对定量数据之间的差异对比关系。与独立样本t 检验相比，配对样本t 检验要求样本是配对的。两组样本的样本量要相同，样本先后的顺序要一一对应。下面建立两组数据，分别代表用方法A和方法B对皮肤弹性相关蛋白C进行10 次测定，比较两种检测蛋白方法是否存在差异，程序与结果如下：

>x<-c（0.82，0.59，0.61，0.61，0.68，0.88，0.65，0.87，0.99，0.91）

>y<-c（0.68，0.56，0.57，0.39，0.39，0.51，0.65，0.71，0.97，0.61）

>t.test（x，y，paired=TRUE）

## Paired t-test

## data：x and y

## t=3.7119，df=9，p-value=0.004831

## alternative hypothesis： true difference in means is not

equal to 0

## 95 percent confidence interval：

## 0.06131851 0.25268149

## sample estimates：

## mean of the differences

## 0.157

结果表明，两种化妆品有显著差异（p 值=0.004831）。

3 方差分析及多重比较

若统计对象为两组以上的独立样本则需要运用方差分析。方差分析的目的在于从试验数据中分析出显著影响因素，以及各个因素间的交互影响，以确定各个因素在该研究中的作用大小。功效评价研究涉及的方差分析大多为单因素方差分析和协方差分析两种。

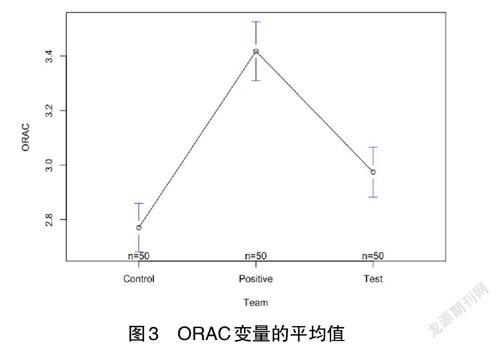
例如，针对某化妆品原料抗氧化能力测试结果，分析3 个研究组中抗氧化能力指数（ORAC）是否存在显著性差异，如果有差异，说明哪组之间的抗氧化能力指数有差异。首先，对变量的平均值进行可视化，程序如下：

> Testdata<- read. csv（"/Users / Desktop / Testdata. csv"， header=

TRUE）

> library（gplots）

> plotmeans（ORAC～Team， Testdata， xlab= "Team"， ylab="ORAC"，main=""）

从图3 中可以看出，t1（control）组、t2（positive）组和t3（test）组平均值之间有差异，但这种差异是否显著，可使用单因素方差分析来验证。用aov（）函数进行单因素方差分析：

> Testdataaov<-aov（ORAC～Team， Testdata）

> Summary（Testdataaov）

## Df Sum Sq Mean Sq F value Pr（>F）

## Team 2 10.98 5.489 47.36 <2e-16 ***

## Residuals 147 17.04 0.116

## ---

## Signif. codes： 0 ‘*** 0.001 ‘** 0.01 ‘* 0.05 ‘.

0.1‘ 1

由于结果中p 值远小于0.05，说明三组ORAC平均值不完全相等。接下来分析哪些组之间的平均值相差较大，使用TukeyHSD（）函数对方差分析的结果进行多重比较，程序如下：library（ggplot2）

tky<-TukeyHSD（Testdataaov）

> tky=as.data.frame（tky$Team）

> tky$pair=rownames（tky）

> ggplot（tky，aes（colour=cut（`p adj`，c（0，0.01，0.05，1），label=c（"p<

0.01"，"p<0.05"，"Non-Sig"））））

+theme_bw（base_size=16）

+geom_hline（yintercept=0， lty="11"，colour="grey30"，size=1）

+ geom_errorbar（aes（pair， ymin=lwr， ymax=upr）， width=0.2， size=

1）

+geom_point（aes（pair，diff），size=2）

+labs（colour=""）+theme（axis.text.x=element_text（size=14））

对可视化结果（见图4）进行程序验证：

> tukeyHSD（Testdataaov）

## Tukey multiple comparisons of means

## 95% family-wise confidence level

## Fit：aov（formula=ORAC～Team，data=Testdata）

## $Team

## diff lwr upr p adj

## Positive-Control 0.648 0.48679895 0.809201

0.0000000

## Test-Control 0.204 0.04279895 0.365201

0.0089521

## Test-Positive - 0.444 - 0.60520105 - 0.282799

0.0000000

上述计算结果显示，在显著性水平为0.05 的情况下，3 组ORAC值两两之间均有显著差异，与可视化结果一致。

4 卡方检验

t 检验和方差分析主要研究定类和定量数据的差异性，卡方检验则主要用于分析定类数据与定量数据之间的差异。若卡方值越大，二者偏差程度越大；反之，二者偏差越小。简言之，卡方分析是用来判断两个样本间的差异程度，从而推断两个变量之间有没有关系。常见的卡方分析是2×2 列联表形式。例如，评价使用某种化妆品对皮肤弹性是否有影响。在R语言中，使用chisq.test（）函数即可实现卡方检验，可以返回卡方值和对应的p 值，同时还可以计算自由度。但是其对数据集的格式有一定的要求，如下为实际的程序代码：

> Useful<-c（33，42）

> Useless<-c（17，8）

> data<- data. frame（Useful， Useless， row. names=c（"Control"，

"Test"））

> chisq.test（data）

## Pearson's Chi-squared test with Yates' continuity

correction

## data：data

## X-squared=3.4133，df=1，p-value=0.06467> data

## Useful Useless

## Control 33 17

## Test 42 8

t 检验和方差分析都属于参数统计。非参数统计也能计算得出结果，只因为非参数统计没有利用数据的全部信息，从而检验功效往往较低。因此，在条件允许的情况下尽可能采用参数统计，使宝贵的原始数据得到充分利用。数据的正态分布和方差齐性在实际应用过程中，即使不完全满足这些前提条件，在很多时候统计效果也是可以被接受的，只有在严重违背这些前提条件导致统计结果不可信时，才采用非参数统计。用R语言能清楚、便捷、可视化地实现化妆品功效评价数据差异关系的统计分析功能，方便化妆品研究人员更好地设计研究、分析数据，迅速找出差異点并进行下一步研究。