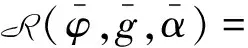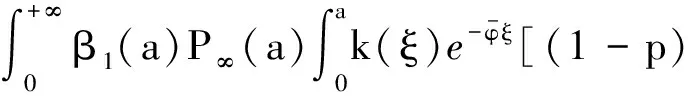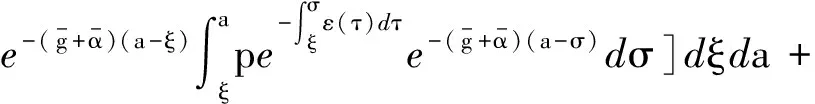一类潜伏期和染病期均具有传染力的年龄结构SEIQR传染病模型及其稳定性
2022-11-04王鑫雨
王 鑫 雨
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
数学建模是研究传染病发展规律,预测其发展趋势的有效方法[1-5].由于不同年龄段人群对传染病的免疫、传播等能力及潜伏期的长短有所不同,因此建立具有年龄结构的传染病模型更具实际意义.而对于传染病的控制和消除,疫苗接种是公认的最实用、有效的方法之一.此外隔离也是控制疫情蔓延的重要手段,无论是2003年爆发的非典(SARS)还是自2019年年底开始的新型冠状病毒肺炎(COVID-19)都是通过隔离手段来切断传染病传播途径,以此控制疫情发展.因此为使模型更加符合实际,许多学者在传染病模型中考虑了疫苗接种和隔离措施[6-9].
发病率是影响传染病传播的重要因素,这取决于人群的行为和疾病的传染性.在流行病学上发病率是单位时间内新感染个体的数量.在与疫情的对抗过程中我们发现多数传染病存在潜伏期,并在潜伏期具有一定传染性.然而潜伏期通常不会表现出染病症状,因此无法对该类人群及时采取有效处理措施[10-11].理论上,潜伏期具有传染力的情况对传染病传播的影响尤为重要,在上述文献中研究者们通常只考虑了染病期具有传染力的情况,且对传染病影响因素及控制措施考虑并不全面.本文在上述研究的基础上进行改进,讨论了一类具有疫苗接种和隔离措施的、潜伏期和染病期均具有传染力的SEIQR传染病模型的稳定性.
1 建立模型
将总人口分为易感类、潜伏类、染病类、隔离类和免疫类五个舱室,分别用S(a,t),E(a,t),I(a,t),Q(a,t),R(a,t)表示t时刻年龄为a的各类人口的密度函数.不考虑因病死亡,易感人群与潜伏类或染病类接触均有可能感染,则年龄结构的SEIQR传染病模型如下:
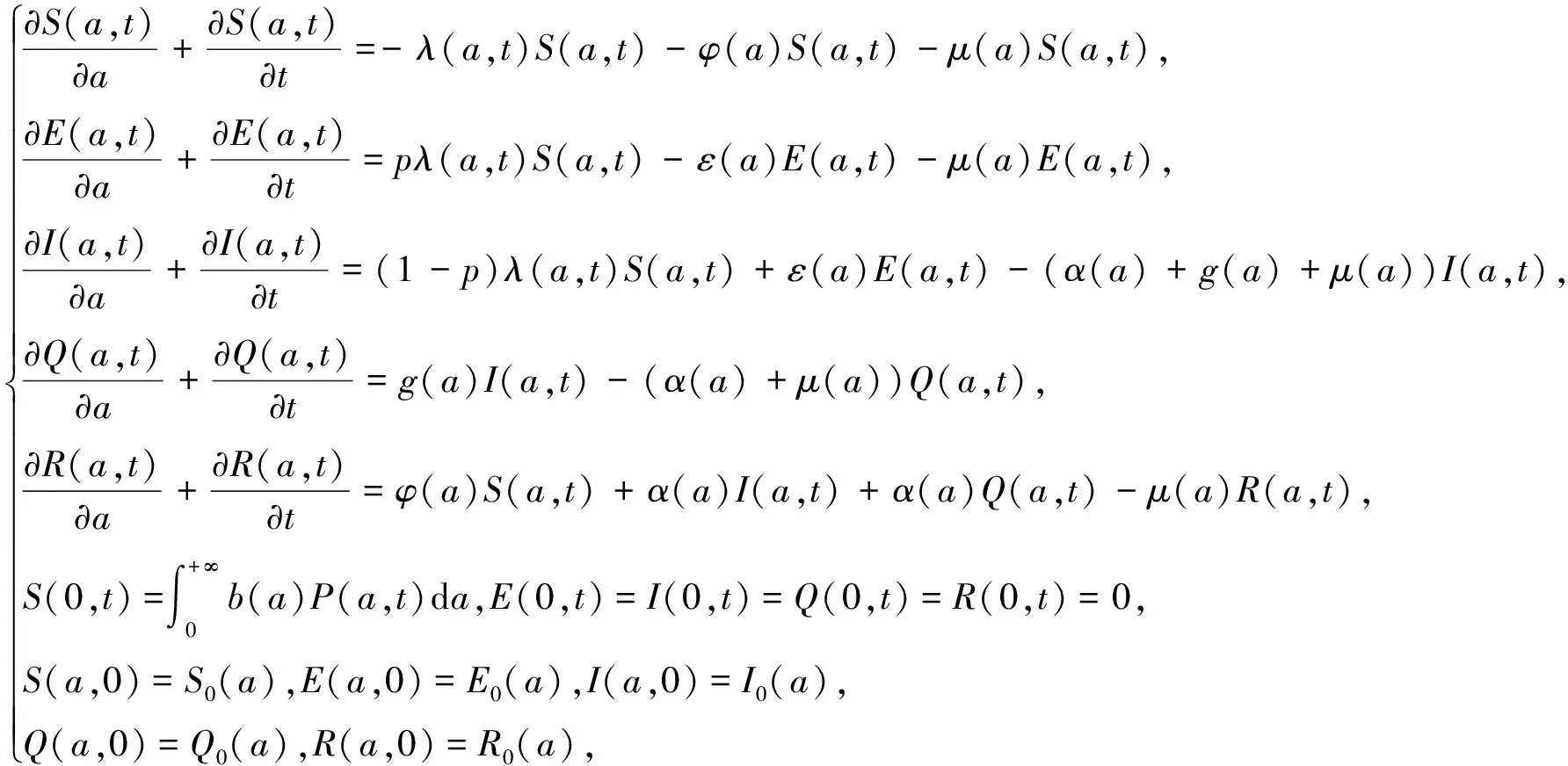
(1)
其中μ(a)为年龄依赖自然死亡率,φ(a)为年龄依赖接种率,[ε(a)]-1为平均潜伏周期,[α(a)]-1为平均染病周期,[g(a)]-1为平均隔离周期,b(a)为年龄依赖出生率.感染率函数为:
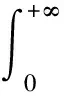
其中βl(a),l=1,2,表示年龄依赖的感染率,k(a)表示年龄依赖的接触率.将(1)的前五个方程相加,得总人口年龄密度函数P(a,t)=S(a,t)+E(a,t)+I(a,t)+Q(a,t)+R(a,t)满足
这是一个标准的Mckendrick-VonForester人口模型[12].假设所有参数都非负,且
b(a),βl(a)∈L∞[0,+∞),l=1,2,
μ(a),φ(a),α(a),g(a),ε(a)∈C[0,+∞),
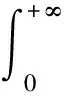
假设当个体超过一定生育年龄时b(a)=0,并假设人口的净再生率为1,即
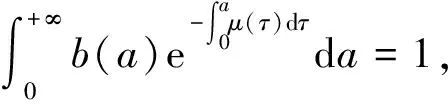
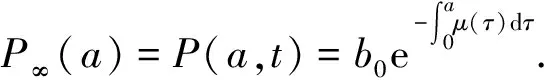
(2)
设S0(a)≥0,E0(a)≥0,I0(a)≥0,Q0(a)≥0,R0(a)≥0,S0(a)+E0(a)+I0(a)+Q0(a)+R0(a)=P∞(a),则有
由(2)得
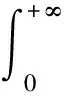
对系统(1)做归一化处理
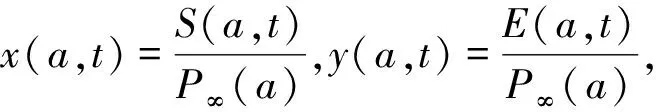
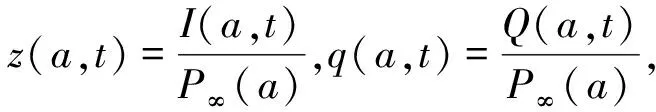
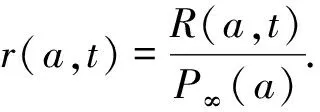
则系统(1)简化为
(3)
2 基本再生数的表达式和无病平衡点的稳定性
本节中我们将得到基本再生数R0和接种再生数R(φ)的表达式,并研究无病平衡点的局部及全局渐近稳定性.
系统(3)的平衡解满足
(4)
初边值条件为
求解(4)易得无病平衡点E0(x0(a),y0(a),z0(a),q0(a),r0(a)),其中
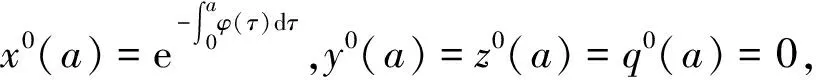
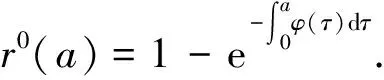
在E0处对模型(3)进行线性化处理,并假设线性化模型具有如下形式的解
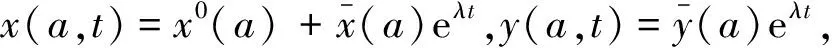
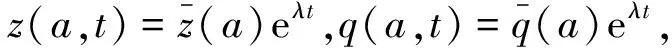
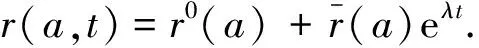
省略高阶项,得
(5)
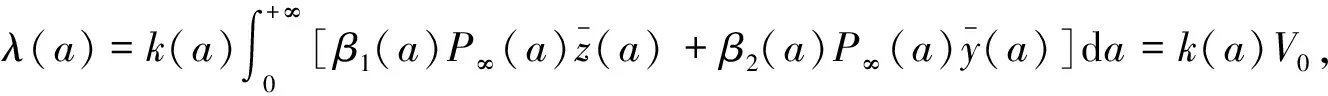
(6)
为常数,由(5)的第二、三个方程得
(7)
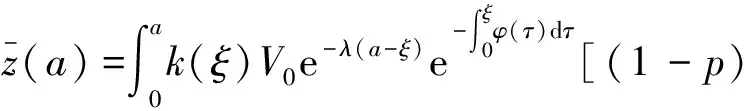
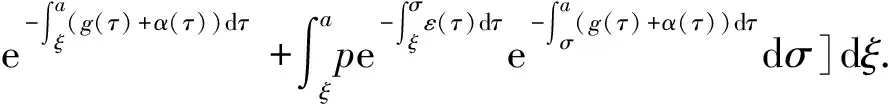
(8)
把(7),(8)代入(6),两边同除以V0(其中V0≠0)并交换积分顺序可得特征方程为
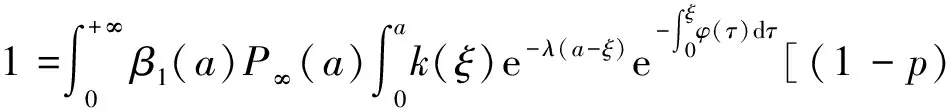
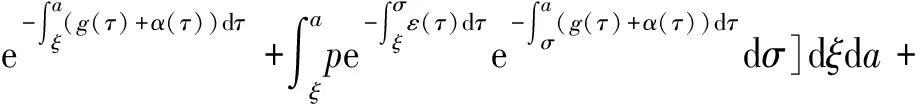
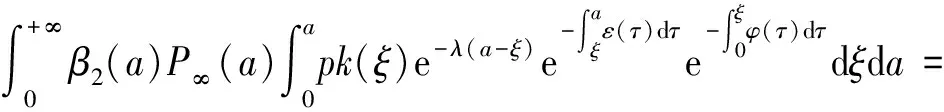
G(λ).
(9)
定义接种再生数R(φ)=G(0),即
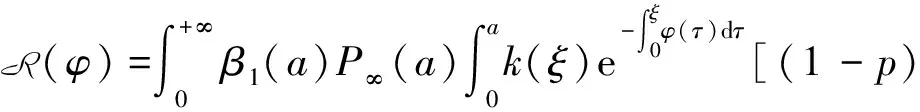
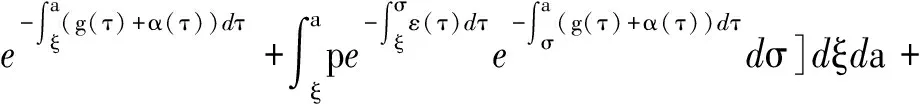
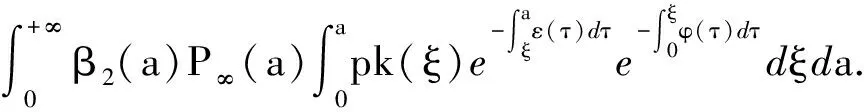
(10)
定理2.1若R(φ)<1,则无病平衡点E0是局部渐近稳定的;若R(φ)>1,则无病平衡点E0是不稳定的.
证由(9)式,当λ取实数时,有
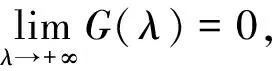
于是G(λ)在(-∞,+∞)上是严格单调递减函数,当G(0)>1,即R(φ)>1时,方程(9)有唯一的正实根,此时E0是不稳定的.当G(0)<1,即R(φ)<1,此时方程(9)有唯一的负实根λ*,λ*是G(λ)=1的占优实根.设λ=x+iy是方程(9)的任意复数根,由G(λ)的递减性及1=G(λ*)=|G(x+iy)|≤G(x),可得Reλ≤λ*.故当R(φ)<1时,E0是局部渐近稳定的.
事实上若不进行疫苗接种,即φ(a)=0,则可得基本再生数
R0=
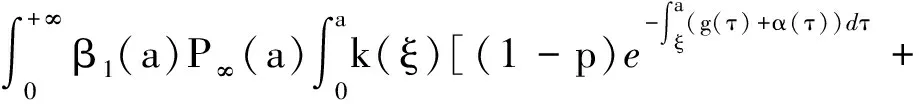
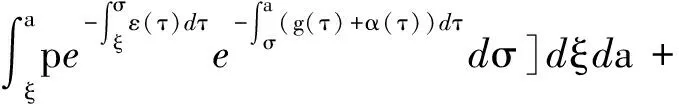
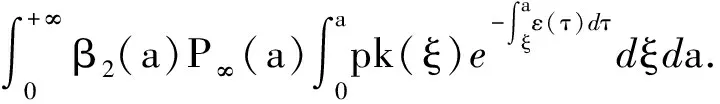
定理2.2若R0<1,则无病平衡点E0全局渐近稳定.
证令f(a,t)=λ(a,t)x(a,t),
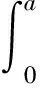
β2(a)P∞(a)y(a,t)]da=k(a)V(t),
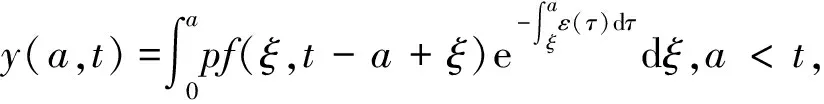
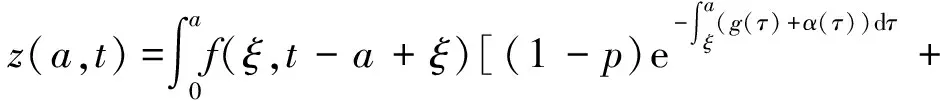
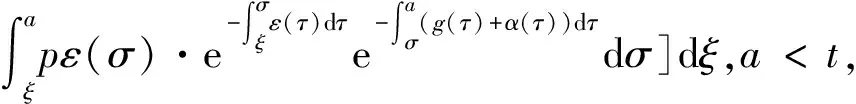
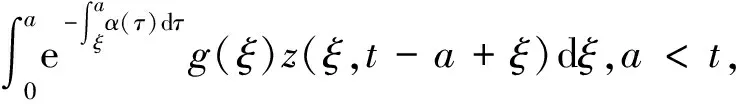
α(ξ)q(ξ,t-a+ξ)]dξ,a 故 f(a,t)≤λ(a,t)= 令 对上式两边取t→+∞时的上极限,由Fatou引理[13]得 令C是常数, 则可得F(a)≤k(a)C,从而 定理3.1当R(φ)>1时,系统(3)存在唯一的地方病平衡点. 证系统(3)有满足如下方程组的正解E*(x*(a),y*(a),z*(a),q*(a),r*(a)) (11) 初边值条件为 其中 V*= (12) 由(11)的第二、三个方程得 (13) (14) 将(13)和(14)代入(12),两边同除以V*(其中V*≠0)并作积分顺序交换,得 :H(V*). (15) 若(15)有一个正解V*,那么系统(3)就存在地方病平衡点,x*(a)+y*(a)+z*(a)+q*(a)+r*(a)=1,且x*(a)>0,那么y*(a)+z*(a)<1,对任意的V*>0,有 其中N是总人口,β+=max{sup[0,+∞)β1(a),sup[0,+∞)β2(a)},若V*=β+N,则H(β+N)<1.又因为H(V*)是关于V*的单调递减连续函数,因此若H(0)=R(φ)>1,则(15)在区间(0,β+N)上存在唯一的正解.即当R(φ)>1时,系统(3)存在唯一的地方病平衡点. 省略高阶项可得 (16) (17) 令 T(λ). (18) 求解(17),得 将y(a),z(a)代入(18)整理得 T(λ)= 定理3.2若 D(a,η)<1,0≤η≤a≤+∞, (19) 则: (1)T(λ)关于λ单调递减,且λ→+∞时T(λ)→0; (2)T(0)<1. 证(1)若(19)成立,由T(λ)表达式可知T(λ)>0,T′(λ)<0,即T(λ)关于λ单调递减,且λ→+∞时T(λ)→0. (2)令λ=0得 dσdξ}da. 由(15)可以看出,上式前两项积分之和为1,而上式第三项积分为负,因此T(0)<1.由定理3.2及T(λ)的表达式可知,方程T(λ)=1有唯一的负实根且所有复根实部都小于这个实根. 定理3.3若假设(19)成立,则系统(14)的地方病平衡点局部渐近稳定.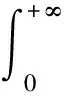
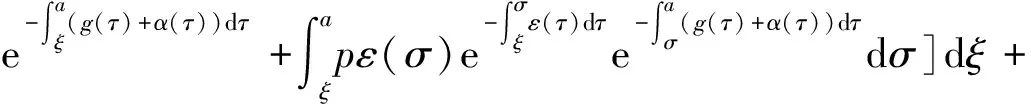
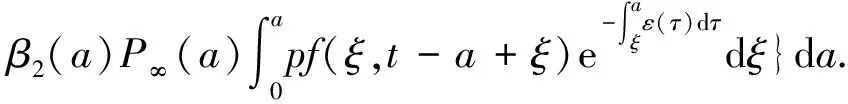
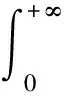
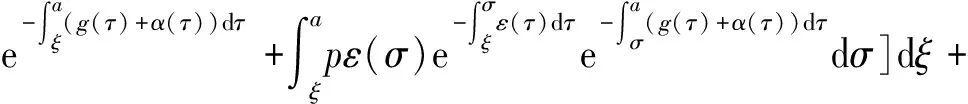
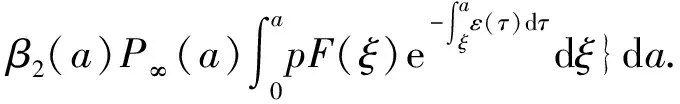
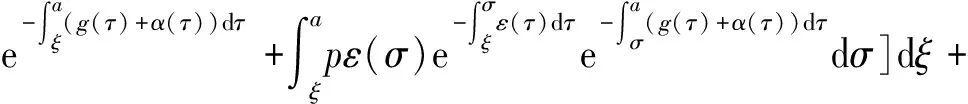
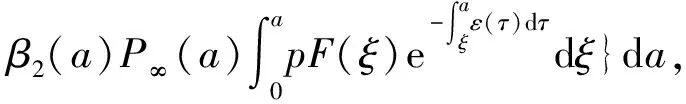
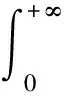
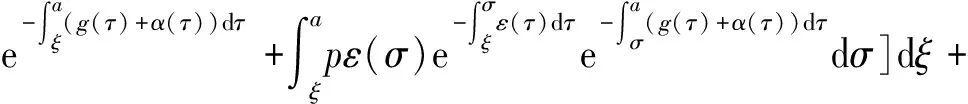
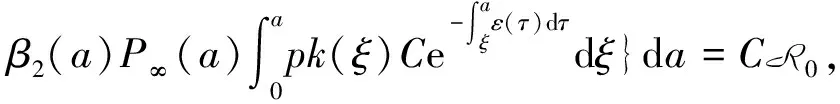
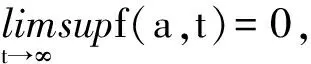

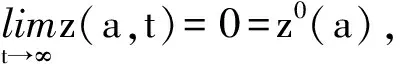
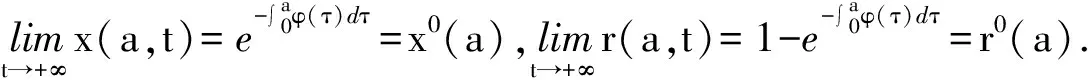
3 地方病平衡点的稳定性
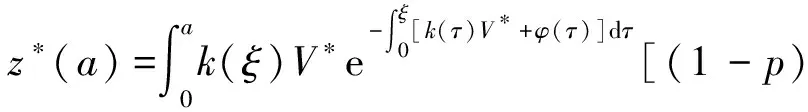
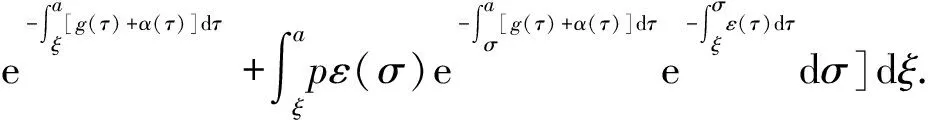
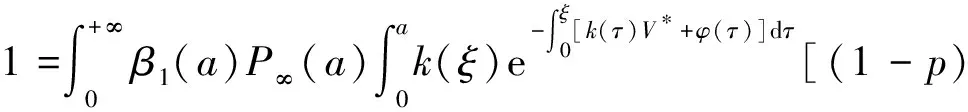
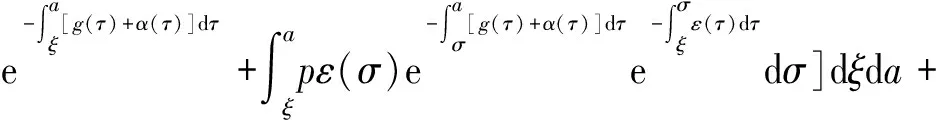
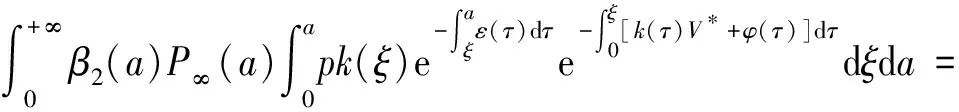
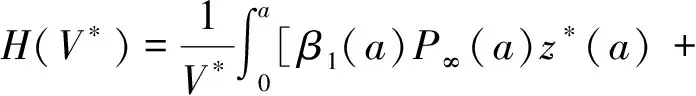
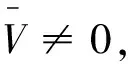
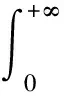
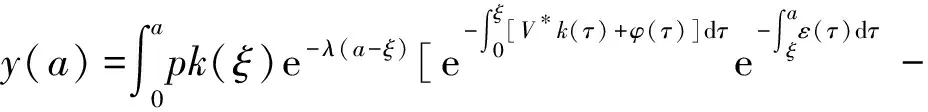
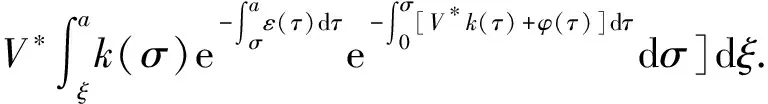
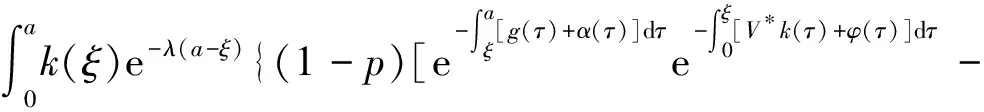

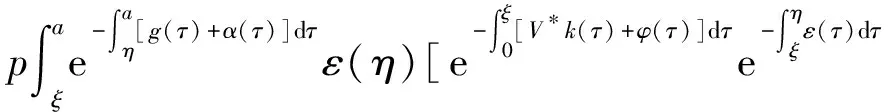
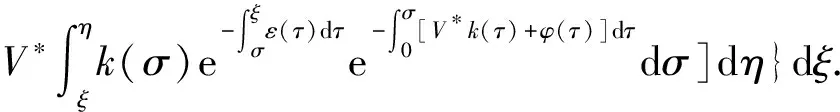
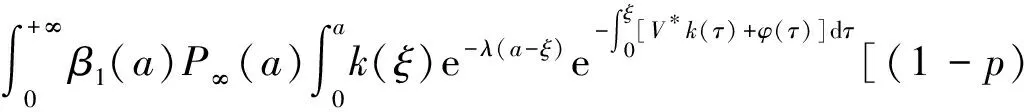
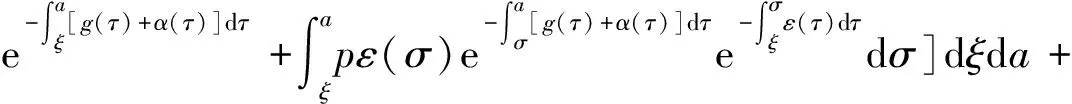
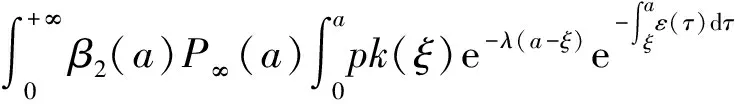
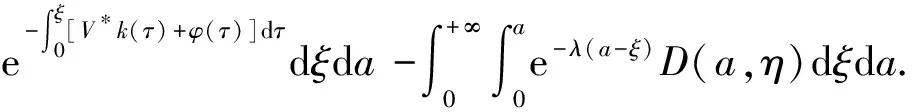
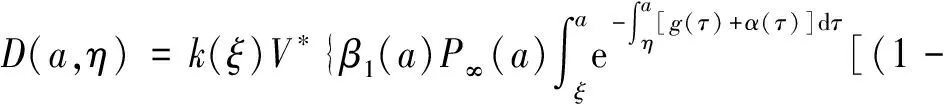
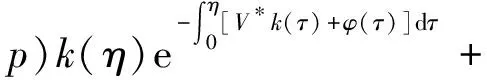
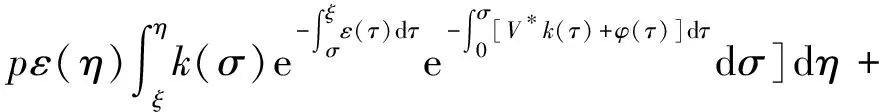
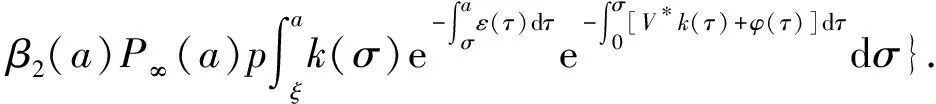
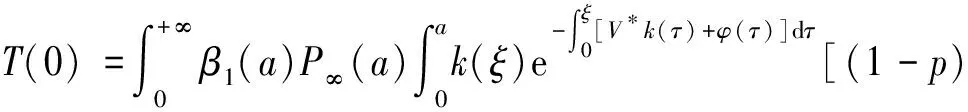
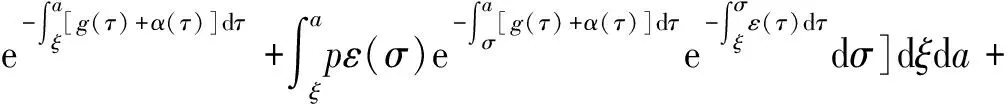
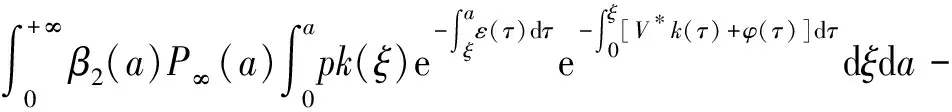
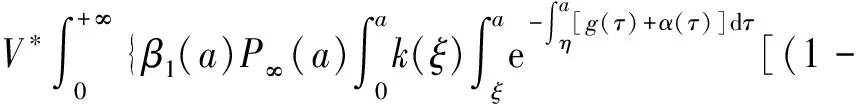
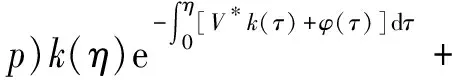
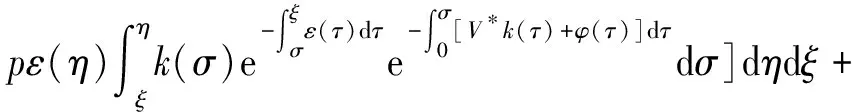
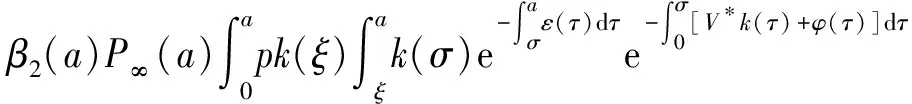
4 讨论